基于正截面承载力及挠度控制的单筋矩形截面梁设计

徐 壮，苏丽梅，张瑞刚

(1.长江水利委员会 河湖保护与建设运行安全中心，湖北 武汉 430014； 2.重庆市万盛经济技术开发区交通局，重庆 400800)

0 引 言

当梁截面尺寸及纵向配筋参数均未知时，传统设计方法是先凭借梁高跨比经验取值假定截面高度，再根据GB 50010-2010《混凝土结构设计规范》(以下简称《规范》)的相关公式进行纵向受力钢筋面积计算及挠度验算。对于单筋矩形截面梁，由于传统方法不能主动控制梁截面混凝土受压区高度，往往会出现少筋梁或超筋梁的现象，还可能不满足挠度验算要求，因而需重复设计，过程繁琐且不直观。张会平[1]推导了单筋受弯构件正截面配筋设计的简化计算公式；张立人等[2]提出利用弦杆法简化计算混凝土受弯构件正截面承载力；曾彬峻等[3]利用罚函数法对钢筋混凝土梁的截面尺寸和钢筋用量进行了优化设计；张鹄志等[4]对不同荷载工况下的钢筋混凝土深梁开展了拓扑优化设计研究。Aschheim等[5]提出了一种用于单轴或双轴弯曲的梁、柱和墙截面配筋设计的直接计算方法。

《规范》提倡采用HRB400和HRB500作为梁的纵向受力普通钢筋，并规定当采用强度等级为400 MPa及以上的钢筋时，混凝土强度等级不应低于C25。因此，本文主要探讨以下不同强度等级的材料组合情况：① 纵筋采用HRB400，混凝土等级为C25、C30及C35；② 纵筋采用HRB500，混凝土等级为C30、C35及C40。当梁的纵向配筋率取经济配筋率[6-7]ρ∈[0.6%，1.5%]，纵筋及混凝土采用以上组合时均为适筋梁。

本文将《规范》相关公式进行简化，在纵向受力钢筋取经济配筋率的条件下，推导出满足正截面承载力要求的梁截面高度计算公式。同时，通过简化得出短期刚度系数的表达式，进而推导出由挠度验算控制的梁截面高度计算公式。综合正截面承载力及挠度验算双重控制计算所得的结果，即可简单便捷地确定合理的梁截面高度。

1 正截面承载力控制的梁高度计算公式

根据《规范》，对于适筋情况下的单筋矩形截面梁，其正截面承载力计算公式为

α1fcbx=fyAs

(1)

(2)

式中：α1为fc的调节系数，当混凝土强度等级不超过C50时，α1取1.0，当混凝土强度等级为C80时，α1取0.94，其间按线性内插法确定；fc，fy分别为混凝土轴心抗压强度设计值和钢筋抗拉强度设计值；b为梁的截面宽度；x为混凝土受压区高度；As为受拉区纵向钢筋的截面面积；M，Mu分别为梁的弯矩设计值和正截面受弯承载力设计值；h0为截面有效高度，h0=h-as，其中h为梁截面高度，as为全部纵向受拉钢筋合力作用点至截面近边缘的距离。

联立式(1)、(2)得

(3)

将梁的纵向受拉钢筋配筋率ρ=As/bh0代入式(3)，根据h0=h-as，取h0≈0.93h[8-9]，则：

(4)

由式(4)可得

(5)

(6)

上述式中：梁的截面宽度b按构造要求确定；当梁的纵向受拉钢筋配筋率ρ∈[0.6%，1.5%]时，截面高度系数α与配筋率ρ的关系如图1所示。

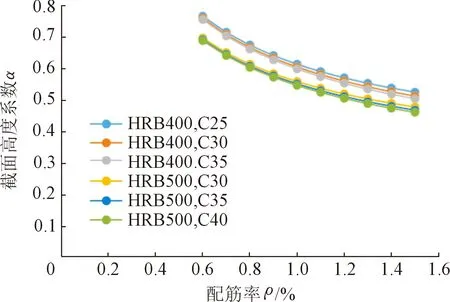
图1 截面高度系数α与配筋率ρ的关系曲线Fig.1 Relation between section height coefficient α and reinforcement ratio ρ

由图1可知，当纵筋的强度等级相同，而混凝土的强度等级不同时，各曲线非常接近。经比较，忽略混凝土强度等级差异的误差变化范围为1.3%～4.1%，能满足工程设计的精度要求。

当ρ=1%时，截面高度系数α的偏上限取值为① 采用HRB400级钢筋时，α=0.616；② 采用HRB500级钢筋时，α=0.561。结合式(6)及图1的变化趋势，并引入配筋率影响系数η，得到梁截面高度的偏上限取值表达式如下。

梁的纵筋采用HRB400级钢筋时：

(7)

梁的纵筋采用HRB500级钢筋时：

(8)

式中：当ρ=1%时，η=1.0；当ρ=0.6%时，η=1.247；当ρ=1.5%时，η=0.856；其他配筋率时根据式(9)依次进行线性插值。

η=0.856+43.44×(1.5%-ρ)

(9)

2 挠度控制的梁高度计算公式

《规范》规定：进行普通钢筋混凝土受弯构件的挠度验算时，应采用荷载准永久组合计算。在余先声、张京穗等[8-9]的研究基础上，设K=Mq/M。其中：Mq为按荷载准永久组合计算的弯矩值，M为弯矩设计值；具体计算见GB 50009-2012《建筑结构荷载规范》及《实用建筑结构静力计算手册》[10]。

设梁的短期刚度为Bs，单位为N·mm2，对于单筋矩形截面梁，根据《规范》有：

(10)

式中：Es，Ec分别为钢筋和混凝土的弹性模量，N/mm2；ψ为裂缝间纵向受拉钢筋应变不均匀系数。令梁短期刚度Bs=βsEcI，其中截面惯性矩I=bh3/12，βs为梁的短期刚度系数。经公式转换可得

(11)

根据《规范》，钢筋牌号为HRB400时Es=2.0×105N/mm2，fy=360 N/mm2；钢筋牌号为HRB500时Es=2.0×105N/mm2，fy=435 N/mm2；C25，C30，C35和C40的Ec分别取2.80×104，3.00×104，3.15×104N/mm2和3.25×104N/mm2，相应ftk分别取1.78，2.01，2.20 N/mm2和2.39 N/mm2，fc分别取11.9，14.3，16.7 N/mm2和19.1 N/mm2。根据本文中的几种不同强度等级材料组合情况，将上述参数代入式(11)得到相应短期刚度系数βs的具体表达式如下。

梁的纵筋采用HRB400级钢筋时：

(12)

梁的纵筋采用HRB500级钢筋时：

(13)

根据《规范》规定：单筋矩形截面梁采用荷载准永久组合并考虑荷载长期作用影响时，其刚度应按式(14)计算。

B=Bs/2

(14)

式中：B为矩形截面梁按荷载准永久组合计算并考虑荷载长期作用影响的刚度。

以承受均布荷载两端简支的单筋矩形截面梁为例，当采用荷载准永久组合时，满足挠度验算要求的梁截面高度计算公式如下。

(15)

式中：f，flim分别为梁跨中挠度和挠度限值；Mq为按荷载准永久组合计算的弯矩值；l0为梁的计算跨度。由式(15)可得

(16)

对于承受集中荷载或其他支承条件的情况，可根据具体条件计算相关参数，参考上述算式推导出相应的计算公式。

3 计算公式应用

3.1 应用步骤

(1) 按构造要求确定梁截面宽度b，并在经济配筋率即[0.6%，1.5%]范围内，选定纵筋配筋率ρ。

(2) 将配筋率ρ代入式(9)，计算得到η。

(2) 根据式(7)或式(8)计算得到满足正截面承载力要求的梁截面最小高度hmin1。

(3) 根据K=Mq/M，计算K值。

(4) 将K值及选定的配筋率ρ代入式(12)或式(13)，求得短期刚度系数βs，再将相关参数代入式(16)，可得由挠度验算控制的梁截面最小高度hmin2。

(5) 取hmin=max{hmin1，hmin2}，并考虑模数要求，从而可确定能同时满足正截面承载力及挠度要求的梁截面高度h。

(6) 取h0≈0.93h，可根据As=ρbh0求出纵向受力钢筋的面积。

3.2 算例验证

3.2.1 算例1

简支矩形截面梁混凝土强度等级为C25，采用HRB400级钢筋，混凝土保护层c=25 mm，承受均布荷载，梁的计算跨度l0=6.0 m。跨中弯矩设计值M=81.2 kN·m，按荷载效应准永久组合计算的Mq=41.7 kN·m，挠度限值flim=l0/250。

3.2.1.1 按本文方法设计

设梁截面宽度b=200 mm，基于随机数学理论方法，利用随机函数RAND在经济配筋率[0.6%，1.5%]范围内随机生成2个ρ值，分别为1.29%、0.88%。

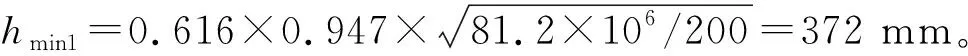
3.2.1.2 按《规范》公式验算

3.2.2 算例2

简支矩形截面梁混凝土强度等级为C35，采用HRB500级钢筋，混凝土保护层c=25 mm，承受均布荷载，梁的计算跨度l0=6.5 m。跨中弯矩设计值M=130 kN·m，按荷载效应准永久组合计算的Mq=60 kN·m，挠度限值flim=l0/250。

3.2.2.1 按本文方法设计

设梁截面宽度b=200 mm，基于随机数学理论方法，利用随机函数RAND在经济配筋率[0.6%，1.5%]范围内随机生成2个ρ值，分别为1.08%、0.75%。

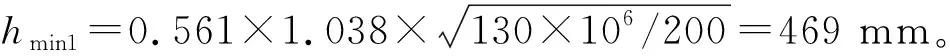
经计算，K=60/130=0.462，由式(13)得βs=0.388，又已知Ec=3.15×104N/mm2，flim=26 mm，将相关参数代入式(16)，可得hmin2=464 mm。

3.2.2.2 按《规范》公式验算

4 结 论

(1) 本文在满足正截面承载力及挠度验算要求的基础上，推导了用以确定纵筋配筋率ρ∈[0.6%，1.5%]时的单筋矩形截面梁截面高度的简化公式，克服了传统方法凭经验取值的不足。通过选取配筋率ρ值并将其他已知参数代入相应的公式，即可得到符合要求的梁截面尺寸及纵向配筋量。

(2) 该方法能主动控制截面混凝土受压区高度，有利于设计的优化，且不需再验算是否出现少筋梁或超筋梁情况，也避免了挠度验算的繁琐过程。同时，梁的延性在经济配筋率范围内能够得到保证。

(3) 由于选配钢筋时，梁的实际配筋量一般会略大于计算配筋量，因而可有效保证设计结果满足要求；但若出现不能满足裂缝宽度要求的情况，则需适当增大配筋量或调整钢筋直径大小。

(4) 对于承受集中荷载或其他支承条件的单筋矩形截面梁，则根据具体情况计算弯矩值，将相关参数代入相应的挠度计算公式，同样可通过类似方法推导出满足挠度验算要求的截面高度计算表达式。