基于神经网络的IGBT模块剩余使用寿命预测模型

2023-01-18郭子庆王学华

电测与仪表 2023年1期

郭子庆，王学华

(华中科技大学电气与电子工程学院，武汉 430074)

0 引言

绝缘栅双极型晶体管(IGBT)是一种功率半导体器件，常用于中高压变流系统如交流电机、开关电源、照明电路等领域。根据一项全行业调查[1]，有31%的受访者表示，功率半导体器件是功率电子转换器中最易损坏的组件。而IGBT是大功率电力电子装备中最为常用的功率半导体器件，在电力系统、高速铁路、汽车、航空中有着广泛应用。

近年来，针对绝缘双极型晶体管可靠性、老化机理以及剩余寿命的研究逐渐兴起。由于IGBT故障发生在10 μs量级的时间尺度上[2]，研究故障后的维修计划没有太多实际意义。更为实际的是，为了防止由于IGBT故障而导致电力电子系统关闭或损坏的情况出现，需要准确预测IGBT元件的剩余使用寿命(RUL)。

目前对于RUL估测的研究主要有两种方案：第一种是直接方法[3]，例如X射线，扫描声学显微镜分析。这类方法需要在研究IGBT的老化机理的基础上，通过观察器件的老化程度从而判断其剩余使用寿命。这种方法判断准确，但是成本较高。并且需要拆卸器件，对装置的破坏性较大[4-5]。第二种方法是基于IGBT老化机理的分析方法。这类方法在了解IGBT内部结构的基础上实施，同时能根据变化的运行条件不断调整。此类分析方法可以根据实际故障机制建立模型，也可以基于数据建立数据驱动的数学模型。数据驱动模型建模过程较为简洁，尤其是在物理模型极其复杂或者限制条件较多的时候，数据驱动方法建立的模型将更加简单和适用。

IGBT模块在使用过程中经过重复的开断闭合后产生老化，相关学者主要将其分为由大电流产生电过应力造成导体损毁腐蚀而引起的键合线脱落和由热循环过程中不同材料产生交变应力引起的焊料层疲劳两种方式[6]。在研究IGBT元件老化的过程中，针对其观测指标，已有团队提出了一系列敏感参数如集射极导通饱和电压VCE(ON)、栅极电压Vge(th)、结温Tj、关断时间Toff、热阻抗Rth等。这些参数中，结温Tj能够很好地反映老化疲劳过程的发展[7]，但Tj的直接测量需要使用温度传感器等元器件，可能会影响老化试验环境同时造成成本升高，因此，选取饱和电压VCE(ON)作为测量量研究结温变化、模块老化、故障诊断等实验更具可行性[8-11]。以饱和电压VCE(ON)作为观测指标的老化规律研究中，使用数据驱动进行预测的模型主要是时间序列模型，对单一指标有良好的预测性能[12]。但目前国内外在使用数学模型的方法进行IGBT寿命预测时，综合多指标建立模型的文献较少，对IGBT分阶段老化过程的机理也未加以利用。

在本研究中，首先对IGBT老化实验数据进行归一化处理，根据已有研究构建包括VCE(ON)和Tj在内的二维参数的IGBT状态检测指标[13]，基于分段拟合的思想将两种老化机理引起的数据变化分离，简要研究了IGBT两种条件下参数与饱和电压V的关系。采用BP神经网络拟合方式研究IGBT模块的老化过程。基于神经网络构建了IGBT模块的老化模型，进而验证多种情况之间RUL预测的准确性。

1 IGBT老化数据处理

1.1 构建包括VCE(ON)和Tj在内的二维参数的IGBT状态检测指标与失效判据

关于饱和电压VCE(ON)、结温Tj、饱和电流ICE等参数之间的关系，相关团队已经可以将它们表示如下[13]：

VCE(ON)(Tj,ICE)=f(Tj,IC)=[V0-a(Tj,Tj0)]+[R0+b(Tj,Tj0)]×ICE

(1)

式中由饱和电压和结温构造的第一项[V0-a(Tj-Tj0)]与状态检测指标成负相关，由热阻抗和结温构造的第二项[R0+b(Tj-Tj0)]ICE与状态检测指标成正相关。文中所使用的实验数据来自于相关公司，根据公司提供的IGBT模块初始参数与市场使用实际情况，将饱和电压高于健康基值5%作为IGBT模块失效的标志，故可以得到失效的表达式为：

VCE(ON)=1.05p1×Tj+1.05p2

(2)

因此，可以将式(1)化为：

X(VCE(ON),Tj)=VCE(ON)-1.05p1×Tj

(3)

式中X(VCE(ON),Tj)为包括了VCE(ON)和Tj的状态检测指标，系数p1=0.002 351。

失效判据化为：

X(VCE(ON),Tj)>1.05p2

(4)

式中，系数p2=1.709。

1.2 分离键合线断裂与焊料层疲劳引起的数据变化

本次实验采用了五个IGBT模块样本，每个模块样本在实验时由两个通道输出采集的数据。五个IGBT模块样本的实验条件如表1所示。

表1 样本实验条件表

老化机理IGBT模块的两种老化机理分别是键合线断裂和焊料层疲劳[14]，在模块经过一次热循环后，如果发生了键合线断裂，饱和电压VCE(ON)将会产生较大变化，而如果没有键合线断裂只有焊料层老化，VCE(ON)的变化将会远小于前述的变化值。在研究老化过程时，使用一定方法将老化机理分离是必要也是可行的[15]。本次实验采集数据所使用的IGBT模块当发生键合线断裂时产生的饱和电压变化将大于0.003 V。数据处理中，先求出每一次热循环过程饱和电压VCE(ON)的变化值，即前后两次VCE(ON)的差值，找到其中大于0.003 V的热循环。剔除掉该次热循环后，将后面的饱和电压数值减去剔除点的差值，使饱和电压关于热循环次数的图像连接起来，达到去除阶跃的效果。热循环次数已经达到万次，焊接层失效是最主要的失效方式。因此，认为可以忽略剔除这些有键合线断裂的热循环轮次对实验结果的影响。使用样本3的数据研究老化的大致趋势，作出饱和电压关于训练次数的图像，如图1所示。

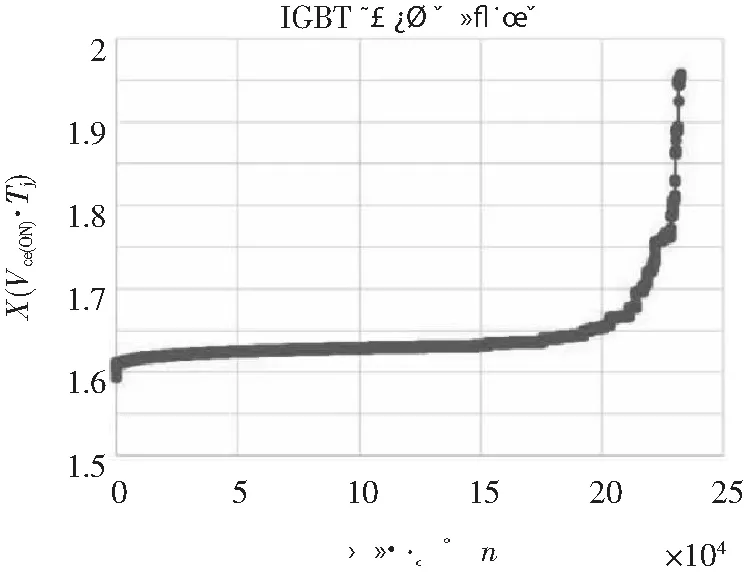
图1 IGBT模块老化曲线

根据以上判别方法，找出这些阶跃点并消除，老化曲线如图2所示。可以看出只考虑焊料层老化时，老化曲线是一条平滑的曲线，为进一步建立老化数学模型提供了可能。

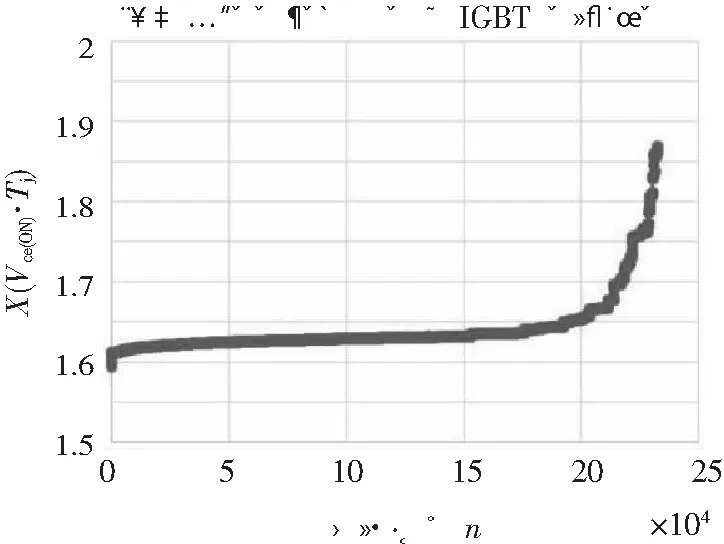
图2 去除键合线断裂影响的IGBT老化曲线

1.3 相关性分析

为了对IGBT模块各项参数有一个初步认识，研究各参数与饱和电压V的相关性。

首先，研究在恒定电流的条件下的关系，使用样本一CH1通道的数据，绘制参数：循环次数n、结温Tj、温差ΔTj之间的矩阵散点图，如图3所示。

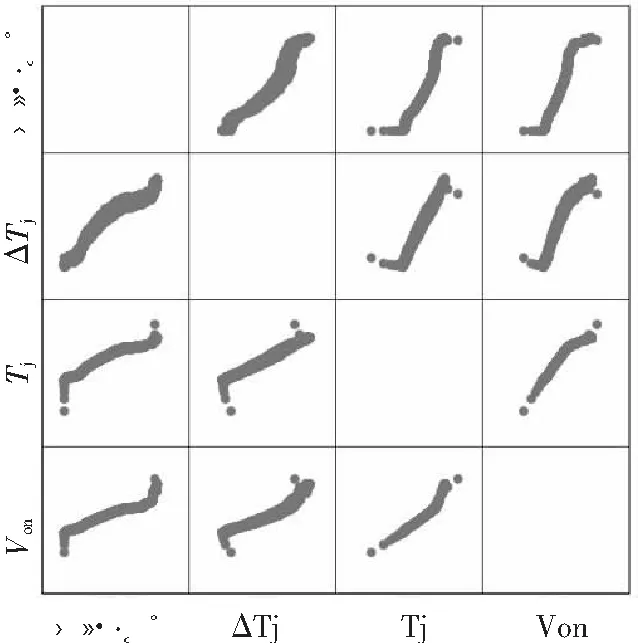
图3 相同电流条件下各参数矩阵散点图

可以看出结温Tj、温差ΔTj都与电压V存在线性关系。采用斯皮尔曼相关性系数对循环次数、Tj、ΔTj三个自变量与电压V的相关性进行分析。使用MATLAB计算三组数据的相关系数RI，并构造正态分布，采取95%的置信水平进行双侧检验，计算得到不相关的概率PI,如表2所示。

表2 同电流条件下各参数与电压的相关性分析表

由计算结果可以得出结论：在相同电流的条件下，循环次数、Tj、ΔTj三个自变量都与电压V有很强的正相关性。

同样在相同温差ΔTj的条件下，采用样本五CH1通道的数据，分析循环次数、结电流Ic、结温Tj三个自变量和饱和电压V之间的关系。仍然采用斯皮尔曼相关系数和95%的置信水平的正态分布假设检验，可以得到分析结果相关性系数R2、不相关概率P2如表3所示。

表3 同温差条件下各参数与电压的相关性分析表

由表3分析结果可以看出：在相同温差的条件下，循环次数、Tj都和电压V有很强的正相关性，而Ic和V则有很强的负相关性。

2 使用回归分析探究老化趋势

同样在样本3数据的基础上，去除数据最前端误差较大的数据，使用MATLAB的curve fitting工具箱分段拟合饱和电压关于热循环次数的曲线。前125 000次热循环的数据使用直线拟合，设拟合函数为：

f(x)=P1×x+P2

(5)

经过MATLAB的curve fitting工具箱拟合后可以得到如下结果。

P1=9.693exp(-8)，置信区间是(9.688e-8,9.698e-8)；P2=1.591，置信区间是(1.591,1.591)。

拟合结果如图4所示。可以看出前半段数据使用直线拟合的效果较好。

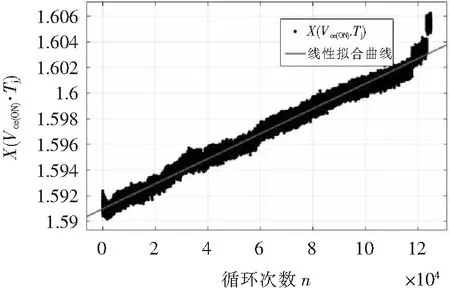
图4 老化第一阶段一次函X数拟合结果图

从第125 000次热循环开始的数据使用双指数函数拟合，设拟合函数为：

f(x)=a×exp(b×x)+c×exp(d×x)

(6)

使用curve fitting工具箱拟合得到：

a=1.63 (1.63,1.63);

b=1.004exp(-7)(9.866exp(-8),1.021exp(-7));

c=3.851exp(-5)(3.764exp(-5),3.937exp(-5));

d=8.487exp(-5)(8.465exp(-5),8.509exp(-5))。

老化第二阶段拟合结果如图5所示。可以看出使用双指数函数拟合后的效果和原始IGBT老化趋势基本吻合。

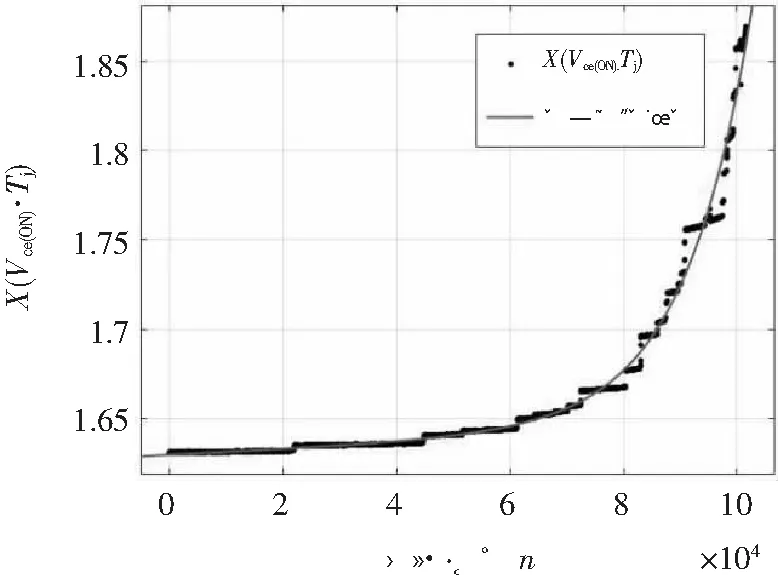
图5 双指数函数拟合结果图

使用回归分析法分段拟合出IGBT模块老化曲线，可以发现其老化指标随着热循环轮次的变化基本可以用一段一次函数和一段双指数函数来描述，但这种分析仅是利用了已有数据归纳出老化过程中老化指标变化的大致趋势，并不能做到预测剩余寿命的功能。

3 使用神经网络构建IGBT模块老化模型

3.1 恒定Ic，V=f(Tj，ΔTj，n)的同样本不同通道之间的数据进行预测

实验中各项参数自变量与电压的输入输出关系难以保证是线性的，而BP神经网络具有良好的非线性映射能力和泛化能力[16]，因此采用BP神经网络进行分析，使用MATLAB的神经网络拟合工具箱即可完成BP神经网络的构建。选取样本1的CH1通道数据，在恒定Ic=595 A，起始Tj为100 ℃的情况下，找寻V和Tj、ΔTj以及循环次数n之间的关系，因此自变量即输入数据为Tj、ΔTj和n，因变量即输出数据为饱和电压V。将数据用神经网络训练，参数设置如下：

设定第一隐藏层为10，第二隐藏层为0，最大训练次数为1 000，最大训练时间为正无穷，最大不下降步数为6，误差目标为0，循环次数为15，采用trainlm函数进行训练。

为了保证可靠性，选取70%的数据用于训练，15%的数据用来测试，15%的用来验证，训练39次，得到如图6所示结果。

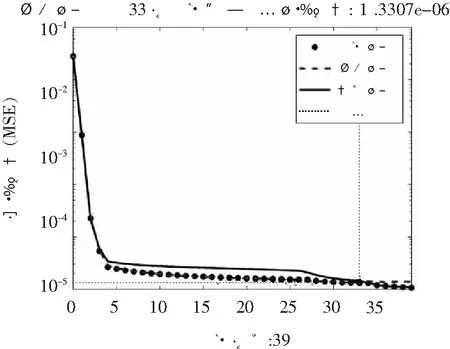
图6 样本1神经网路拟合均方误差收敛图

可以看到在样本训练33次之后，均方误差已经足够小，可以视为0。同时给出原始数据与神经网络拟合得到的数据的相关性分析如图7所示。

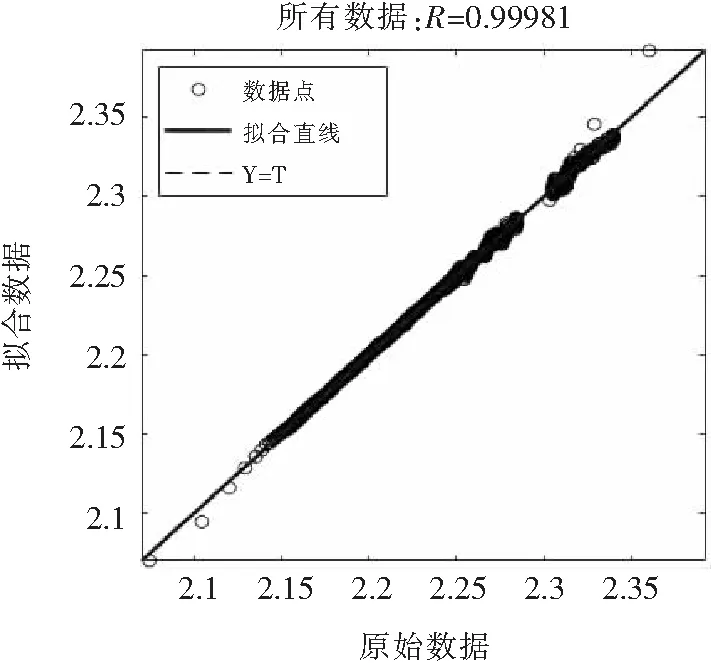
图7 相关性分析图

R近似为1，可以原始数据与拟合数据有着强烈的正相关性，初步按断拟合效果应该较好。再给出具体的误差分析图谱如图8所示。

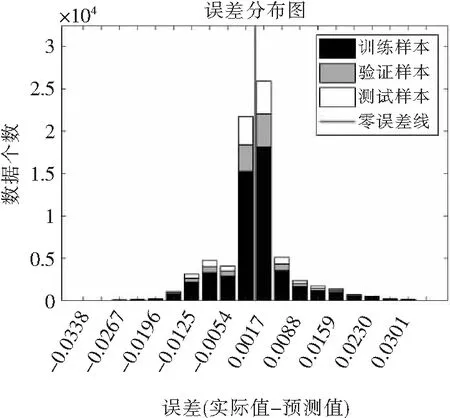
图8 误差分布图

所有的样本点都集中在零误差线附近，大于3σ的样本点几乎为0，且误差为10-3级别，非常小。因此认为该训练样本数据后的模型非常准确，以此来预测样本1的CH2通道的数据，和其实际的情况进行对比。将预测数据和实际数据之间进行比较，得到实际的误差分布图如图9、图10所示。

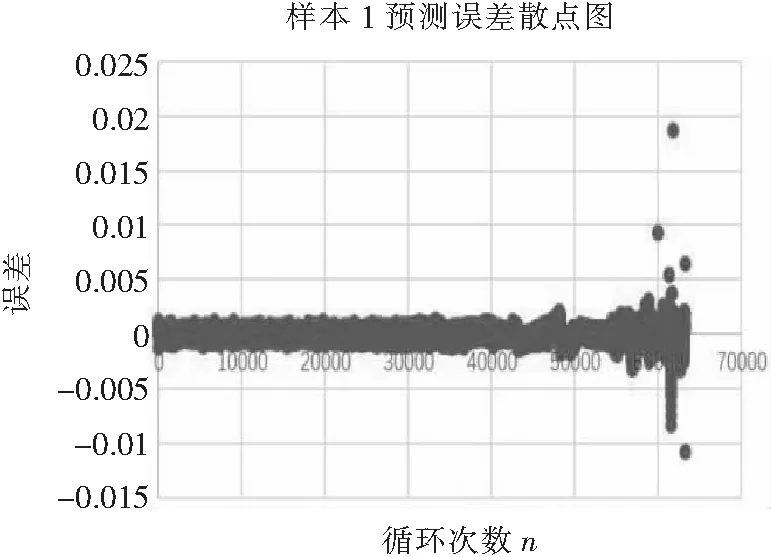
图9 样本1预测误差散点图

图10 样本1预测实际误差分布图

预测误差呈现类似正态分布的特征。初步猜测，这个误差是由于Ic不同而导致的，样本1的CH2通道的Ic保持在恒定的589 A，对应的样本数据中的饱和电压V已有约0.048 V的差别。同时元件初始时刻的实验数据并不精确，在一定的实验次数之后才能达到稳定。

3.2 恒定Ic，V=f(Tj，ΔTj，n)同样本同通道之间的数据预测

选取样本2的CH1通道的前60 000个数据进行训练，预测后14 000余个数据，同样，自变量为Tj、ΔTj和n，因变量为V。神经网络各项参数同上一实验相同，在训练408次后达到最优解，如图11所示。

图11 样本2神经网络拟合均方误差收敛图

将预测数据和实际数据进行比对，进行误差分析，结果如图12、图13所示。

可以发现预测数据的前半部分误差基本集中分布在0.001～0.015左右，相比于自身5%的老化基准，要至少上升0.1左右才能到达老化，误差是其的百分之一，可以忽略不计。预测数据仅在后半部分出现了超过0.02的较多误差。因此该方法对于自身的数据预测具有比较好的吻合性。但由后半部分的误差分析可知，方法在预测数据过多的时候会出现较大的正数误差，因此训练数据和预测数据之间比例不宜过小。

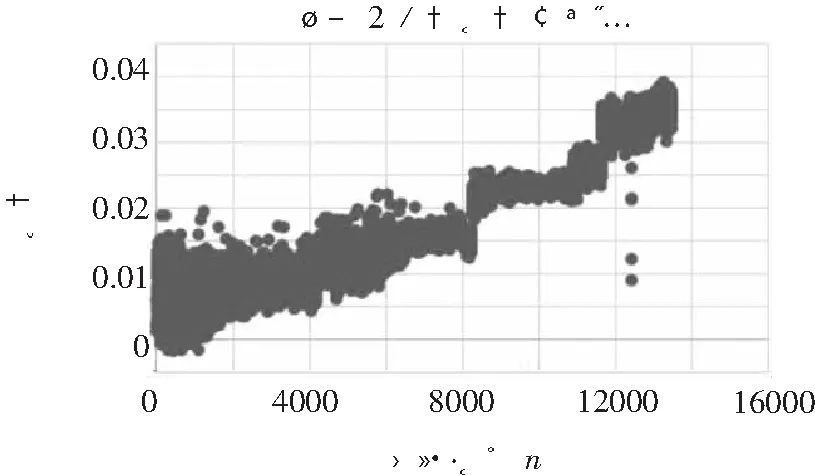
图12 样本2预测误差散点图

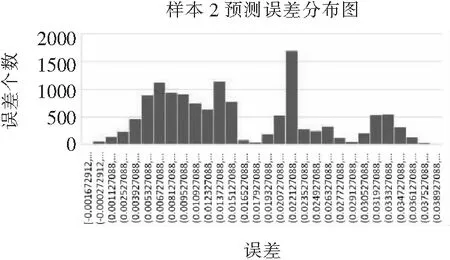
图13 样本2预测实际误差分布图

3.3 恒定ΔTj，V=(Ic，Tj，n)同样本不同通道之间的数据预测

采用样本5的CH1通道的数据，恒定ΔTj=80 ℃，剔除不稳定点前40个数据进行预测，找寻V和Ic、Tj和n之间的关系。此时，自变量为Ic、Tj和n，因变量为V，继续采用神经网络训练，参数同前，训练3157次，在351次时候找到最优解，并以此预测CH2的样本数据。

结果发现在不同的CH下预测效果并不好，会存在比较大的误差，并且误差没有任何的逻辑可言，如图14所示。

初步分析原因有，在不同工况下，虽然ΔTj是一样的，但是Tj的初始值会对结果产生较大影响，这一点通过简单的神经网络训练是难以发现的。因此这种情况下并不适合用这种方法求解。

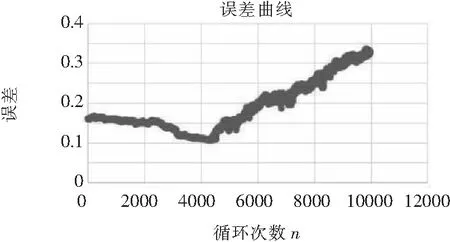
图14 样本5双通道预测误差曲线图

3.4 恒定ΔTj，V=(Ic，Tj，n)同样本同通道之间的数据预测

采用样本5的CH2通道的数据，通道前8 000个数据用来训练，后2 000个数据进行预测分析,变量和参数设置同前，训练37次后于35次找到最优解，得到预测数据和实际数据的误差分析如图15、图16所示。

图15 样本5单通道预测误差散点图

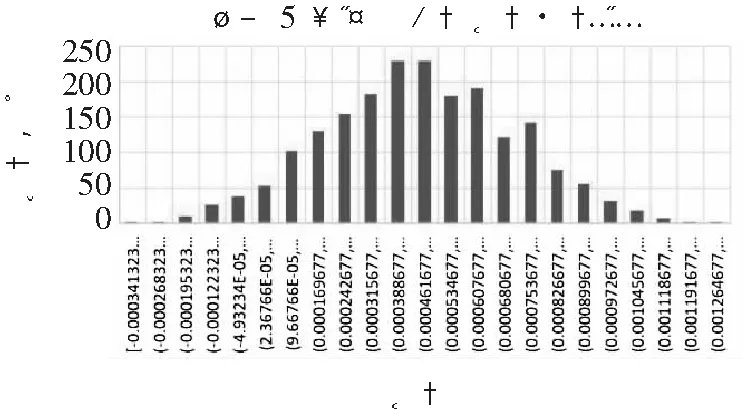
图16 样本5单通道预测实际误差分布图

基本误差集中在0.004左右，和之前的第一种情况预测类似，并且误差也有类似正态分布的特点，可以适当拟合函数加以消除，但其本身已经足够小，相比于5%的老化标准而言可以忽略不计。

由以上的实验结果可以分析得到，对于相同Ic的情况，不同工况之间可以利用神经网络相互预测，但是需要知道Ic所带来的误差影响，这需要进一步深入分析其物理模型，而同种工况之间的预测则十分完美。而对于相同的ΔTj，同种工况的预测效果依然很好，但不同工况的预测性非常差，因此还需要其他的算法来对这种情况进行辅助分析。