基于CEEMD-GRU模型的短期电力负荷预测方法

朱伟，孙运全，钱尧，金浩，杨海晶

(江苏大学 电气信息工程学院， 江苏 镇江 321100)

0 引 言

伴随着科学技术的进步，生产和消费水平的提高，用电设备和用电质量的要求引起了电网公司以及电力工作者们的高度重视[1]。电力负荷预测作为对负荷变化的预先估计和推算，有效地预测和参与电力网的实时调度和运行规划，提前增大或减小供电，减少电网运输中不必要的损失，从而提高经济效益。过去我们往往着重研究发电一侧的工作效益，近年来，随着电网管理的智能化以及基础用电设施建设的逐步完善，如何有效和提高用户侧的管理效益变得越来越重要[2]，因此，对短期电力负荷预测研究成为智能运行和管理电网的重要研究课题。

目前，国内外对电力负荷预测研究已经取得实质性的进展，将传统预测方法、大数据挖掘、人工智能算法相结合，对未来负荷进行预测[3-4]，例如多元线性回归分析、时间序列分析[5]等。利用支持向量机、神经网络等学习方法，使得计算简单并易于实现，更好克服大量时间数据复杂、非线性等缺点，成为如何完善并提高预测结果精确性的重要研究内容之一。文献[6]采用算术优化算法(AOA)和最小二乘支持向量机(LSSVM)的模型，对经过互补集合经验模态分解(CEEMD)和模糊熵(FE)综合处理后的子序列进行预测。文献[7]针对传统负荷预测方法缺少对时序数据相关性、特征值的全面考虑等问题，采用一种优化的VMD-mRMR-LSTM模型，实现对各分量分别预测,将预测结果叠加得到最终的预测值。文献[8]针对原负荷数据的不稳定、非线性，采用EMD分解处理后，通过LSTM模型对每个分量进行预测，将得到的结果叠加重构，获得完整的预测结果，该方法使得训练拟合效果更好，具有较高的预测精度。这些研究为解决电力系统的短期负荷预测提供了理论依据。

针对上述研究背景，文章提出了一种基于CEEMD方法和GRU神经网络融合的预测模型，将电力负荷数据通过CEEMD分解，相比于EMD分解，降低了模态混叠的影响，然后将分解得到的子分量和一个余分量通过优化后的GRU神经网络进行迭代预测，将预测结果进行重构组合，得到完整的预测曲线，通过同条件仿真对比，证明该方法的可靠性和准确性。

1 互补集合经验模态分解

1.1 经验模态分解

在处理时间序列问题时，由于实际的原序列存在着不平稳性，导致预测模型拟合效果差，预测效果不好。EMD分解能对数据进行平稳化处理，分解成一组包含不同时间尺度上的本征模态分量(Intrinsic Mode Function, IMF)和一个残余分量，适用于解决非线性、随机性强、不平稳等的问题。

从理论上讲，EMD分解能够对任意一种类型的序列或者信号进行分解处理，但IMF都必须具备以下条件：(1)在序列内部，极值点的数量和零点数量要么保持相同，要么至多相差一个；(2)对于序列上的任意一点，其局部极小值和局部极大值构成的上下包络线的平均值为零[9]。

EMD分解有以下几个步骤：

(1)假设原始序列为x(t)={x1,x2,…,xi}，求出序列x(t)中所有的极大值点和极小值点，采用三次样条函数，分别拟合出原序列x(t)的上下包络线；

(2)求步骤(1)中拟合出的上下包络线的平均值，记作m(t)，并用原序列x(t)减去均值m(t)，得到的数定义为c(t)，即：

c(t)=x(t)-m(t)

(1)

(3)倘若c(t)不符合IMF的条件，则令x(t)=c(t)，重复进行步骤(1)，直至所得的c(t)符合IMF条件，令求得的c(t)为IMF1；

(4)用原始序列x(t)减去c(t)得到一阶余项r1(t)，即：

r1(t)=x(t)-IMF1

(2)

(5)令x(t)=r1(t)，并重复进行步骤(1)～步骤(4)，直到余项不能继续分解，即函数单调为止，称此时的余项为残余分量，即最终得到n阶IMF和一个残余分量rn，整理后得到：

(3)

然而，在实际情况中，原始序列存在异常情况(如噪声、脉冲干扰等)，导致出现模态混叠的现象，即一个IMF分量存在其他尺度的分量。

1.2 互补集合经验模态分解

针对模态混叠现象，Huang提出了集合经验模分解(Ensemble Empirical Mode Decomposition, EEMD)，通过加入辅助白噪声，平滑信号脉冲产生的干扰，当经过足够多的全体均值后，噪声将会消除，全体的均值就可以认为是最终的结果[10]。

但是，往往添加的白噪声很难做到完全消除，所以伴随着分解，往往会给重构后的结果带来另外的噪声误差。为此，文献[11-12]对EEMD方法进行改进，提出了CEEMD方法，该方法添加一对符号相反的辅助白噪声，然后进行EMD分解，这样做的好处是，既抑制模态混叠的出现，又减少了因添加白噪声产生的干扰，使得分解效果更好。

CEEMD分解方法包括以下几个步骤：

(1)对原始的序列，添加n对正负相反的白噪声，可以得到以下两个集合：

(4)

式中S为原始序列；N为添加的辅助白噪声；M1、M2分别为加入正负白噪声后得到的序列，即共2n组IMF分量；

(2)对两个集合都进行EMD分解，并将第i个序列的第j个IMF分量记作cij；

(3)再把得到的2n组IMF取平均值，得到最终叠IMF分量为：

(5)

要注意的是，该分解方法在使用前，需设置两个额外的参数，即辅助白噪声的幅值H和对数N。一般的，当对数N取100时，幅值H的取值范围为0.01～0.1。

2 门控的循环神经网络

2.1 循环神经网络

循环神经网络(Recurrent Neural Network, RNN)，是一类用于处理序列数据问题的神经网络，与一般的前馈神经网络相比，隐藏层加入了自反馈结构，使得同一层的神经元信息相互传递[13]。RNN主要是由输入层、隐藏层、输出层3个部分构成，其隐藏层展开结构如图1所示。

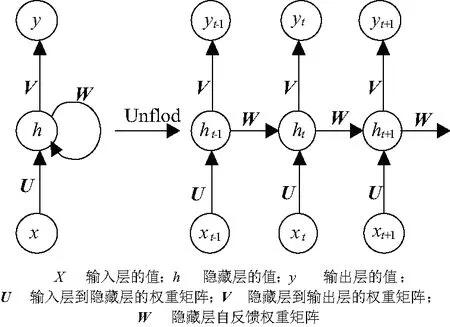
图1 循环神经网络结构图Fig.1 Structure diagram of cyclic neural network

规定一条时间序列为x={x1，x2，…，xn}，则在t时刻有：

ht=f(Uxt+Wht-1+bh)

(6)

yt=g(Vht+by)

(7)

式中ht表示当t时刻时隐藏层内的值；yt表示当t时刻时输出层内的值；bh、by分别表示隐藏层与输出层在计算式中的偏置项；f()、g()分别表示隐藏层和输出层的计算公式，即激活函数。

信息传递一般包括以下几个步骤：

(1)前向传播，即根据给出的x得到输出的y；

(2)反向传播，即计算每个位置的损失函数和最终损失L；

(3)优化减小误差项值，并计算每个权重。

虽然RNN具有记忆性、参数共享等优点，但在处理实际跨度较大、依赖性强等问题时，同一隐藏层中信息传递会出现梯度消失、爆炸等问题，从而导致学习效率低，结果较差。

2.2 门控的循环神经网络

尽管LSTM解决了RNN长期依赖性问题，但是其参数设置多，收敛速度慢，降低了训练效率。GRU神经网络，是LSTM神经网络的一种变异体，更新门代替了LSTM的输入门和遗忘门，另外还有一个重置门[14]，如图2中的zt和rt所示。

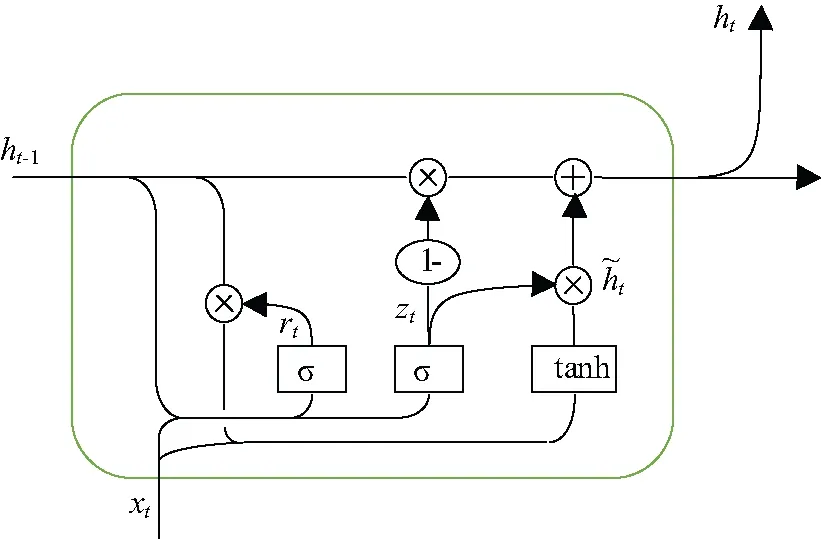
图2 GRU网络隐藏层的结构

更新门确定上一个隐藏层有多少信息传递给当前隐藏层中，重置门确定忘掉过去多少状态信息量的程度[15-16]。门结构工作情况可用数学式表示为：

rt=σ(Wr·[ht-1，xt]+br)

(8)

zt=σ(Wz·[ht-1，xt]+bz)

(9)

式中W和b分别为其对应门的权重矩阵以及偏置项；σ为sigmoid激活函数，它能够将值映射到[0,1]范围内，从而实现门控。

将数据序列带入GRU神经元，计算得到输出值后，通过均方差(Mean Square Error, MSE)公式，计算得到每个神经元的误差，具体计算公式为：

(10)

式中xi和x′i分别为序列的实际值和预测值；n为序列的总数；i为序列的序号。

2.3 基于CEEMD-GRU的预测模型

基于CEEMD-GRU的短期电力负荷预测方法一般步骤是：

Step1：输入历史负荷数据，对负荷数据预处理，包括将异常的数据剔除、均值法补充空缺数据、进行数据归一化等；

Step2：对电力负荷序列进行分解处理，减少非线性、非平稳性对模型构建带来的影响。利用CEEMD方法处理原始序列，得到一组IMF分量和一个残余分量rn；

Step3：对各个序列分量分别构建GRU神经网络预测模型，利用算法对网络超参数进行优化；

Step4：将优化后的超参数带入各自的GRU网络模型中，采用单步预测，输出各自的预测分量，将分量叠加重构后，得到完整的预测结果。

其中，CEEMD-GRU网络预测流程如图3所示。

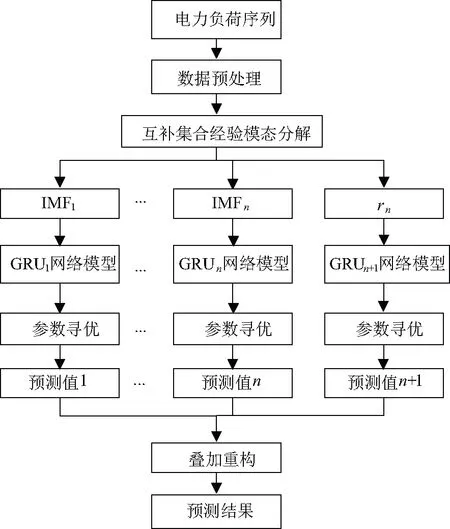
图3 CEEMD-GRU神经网络预测模型结构

3 实例分析及结果展示

3.1 预测模型评价指标

一般的，我们在预测结果时会存在误差值，由于时间序列预测的随机性和不确定性，这些误差都是难以避免的[17]。为了更好了解和评定预测模型，我们有很多评价指标，常用的评价指标有相对误差(yRE)、均方根误差(yRMSE)、平均绝对百分比误差(yMAPE)等[18]：

(11)

(12)

(13)

3.2 数据展示与分析

文章采用的数据来自于某市2018年7月6日～2018年7月25日的电力负荷数据，其采用间隔为15 min，即一共选取1 920条数据，如图4所示，可以发现其周期性和季节性不明显。文中构建时间序列数据进行训练和测试，以一天的采样长度做窗口滑动处理，即以96组数据的时间点为特征，下一个时间点数据为标签。依次带入模型训练，最终预测7月25日的负荷曲线。实验所使用的仿真平台为MATLAB2016b版，电脑配置为i7-7700HQ处理器，8 GB内存，训练环境是GPU。

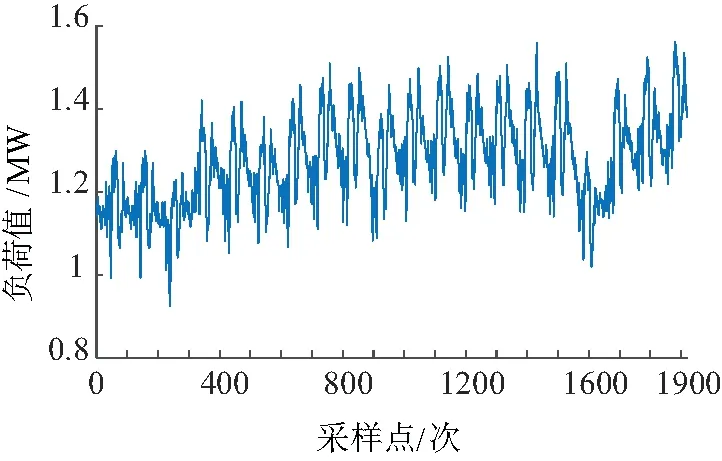
图4 电力负荷原始序列

从图4中可以看出，原始负荷序列存在高频分量、噪声，如果直接输入则会出现预测模型拟合困难等问题，需对原序列进行分解，降低这些影响。分别采用EMD、EEMD、CEEMD方法分解，比较三种方法的优劣性，其中加入白噪声的幅值H为0.1，集成对数N为100，CEEMD分量上限设置为9。图5为三种方法重构后的误差。

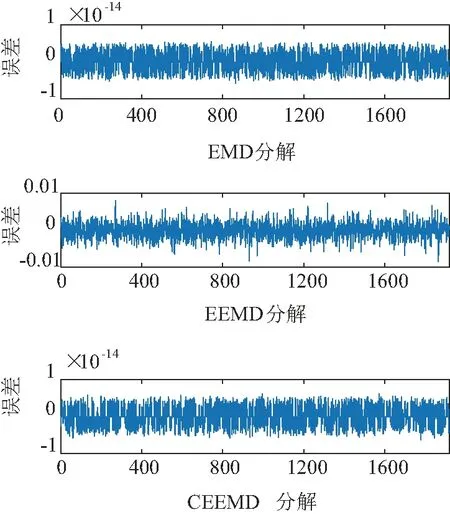
图5 三种分解方法的重构误差

从图5可以看出，EEMD分解使得重构后的误差显著增加，而采用CEEMD分解将白噪音在各次分解中分别带入抵消，故重构后的误差又回到原来的数量级，保证后面的预测结果，验证该方法的有效性。

接下来，采用CEEMD方法分解原序列，结果得到9组IMF分量和1组残余量，如图6所示。

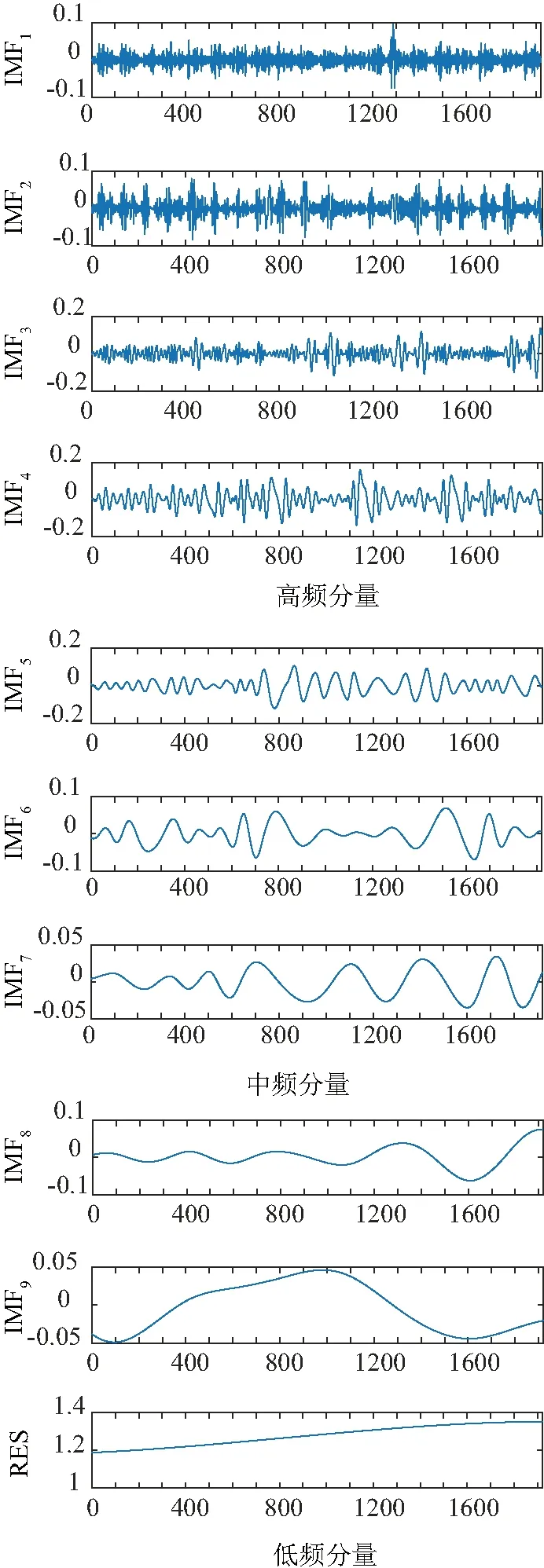
图6 电力负荷数据的CEEMD分解

为衡量分解子序列的有序性，根据香农信息论，利用自信息熵H(Xi)来表征向量X自身随机波动的不确定度，即：

(14)

自信息熵H(Xi)的值越大，表示系统随机波动程度大，系统越混乱；反之，则表示系统随机波动程度小，系统越有序。表1为CEEMD分解的本征模态分量的自信息熵值。

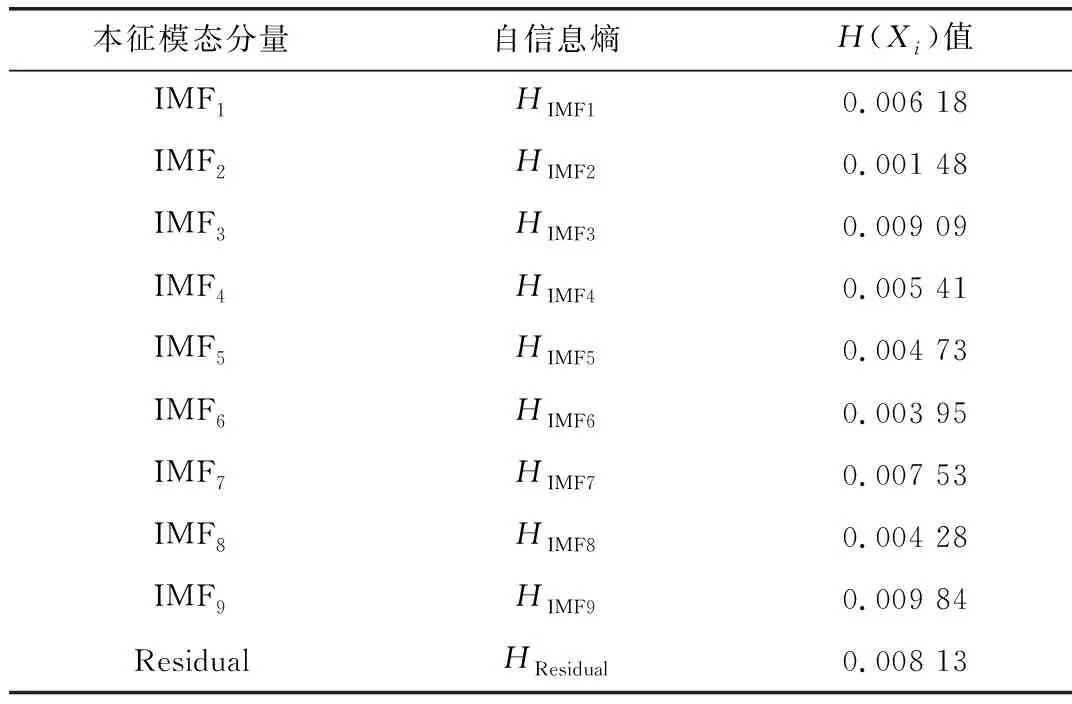
表1 各本征模态分量自信息熵值

观察表1中数据可知，各本征模态分量的自信息熵均低于0.01，属于低自信息熵，即各个本征模态分量均有序，分解效果好。将各个模态分量序列进行归一化，并分割成训练集和测试集，归一化公式为：

(15)

式中xmax、xmin分别为样本数据中的最大值和最小值；yi为采样点i经过归一化后的数据。

3.3 实验结果及其分析

为验证所提出的模型的有效性，分别使用CEEMD-RNN、CEEMD-BP、GRU和CEEMD-GRU模型在同一数据集上进行预测，其中，初始化神经网络模型的学习率lr为0.001，隐藏层层数为1，隐藏层神经元个数m为200，采用Adam算法训练超参数，最大迭代次数取100。实际值与预测值曲线如图7所示。

图7 CEEMD-GRU模型的电力负荷预测及其与GRU、CEEMD-RNN、CEEMD-BP模型的对比

从图7可以看出，各个模型在波动较小的部分预测效果都不错，CEEMD-RNN和CEEMD-GRU模型的预测精度明显高于采用CEEMD-BP模型，对负荷序列预测有着较好的拟合效果。并且，在原始序列的波动阶段，采用CEEMD分解的模型预测误差优于未采用分解方法的模型，见图7中6:00～8:00时刻。图8为CEEMD-GRU模型及其与其他模型的相对误差。

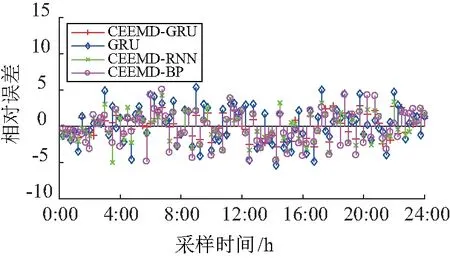
图8 预测模型相对误差对比

从图8中可以看出，采用CEEMD-GRU模型的相对误差主要集中在[-3,3]的区间内，而采用其他预测模型的相对误差范围扩大到[-6,6]区间内，证明了CEEMD-GRU模型相较于其他几种模型有着更好的预测精度。

为进一步研究CEEMD-GRU模型的优势，采用决定系数R2、yMAPE和yRMSE来评估各个模型的预测效果。R2计算公式如下：

(16)

式中xiave为实际值的平均值，评估结果如表2所示。

表2 CEEMD-GRU与其他模型预测结果评估

观察表2中数据可知，在短期负荷预测中，相比于直接采用GRU网络预测，通过采用CEEMD处理原负荷序列的方法，yMAPE值减小0.804，yRMSE值减小0.994，与其他组合方法CEEMD-BP、CEEMD-RNN比较，CEEMD-GRU的yMAPE值分别减小0.741、0.442，yRMSE的值分别减小0.859、0.5。从决定系数R2来看，CEEMD-GRU网络预测模型拟合优度更高，即更加接近于实际情况，预测精度高。图9为CEEMD-GRU模型的预测散点图。

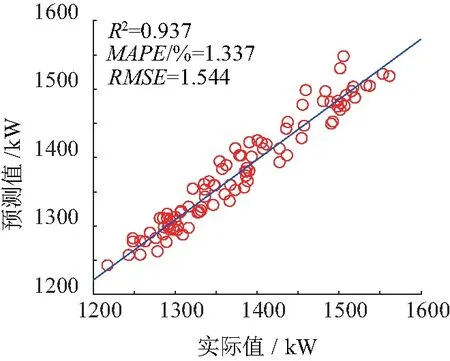
图9 CEEMD-GRU预测散点图

4 结束语

文章围绕电力负荷短期预测提出了基于CEEMD-GRU神经网络的预测方法，得到以下结论：

(1)原始电力负荷数据由于时间跨度长、随机性大，导致其存在非线性、非平稳性等问题，如果直接带入预测模型则会导致训练出来的模型拟合效果不好，预测精度降低。文章采用CEEMD分解，将原序列分解成一组IMF分量和一个残余分量rn，通过平稳化处理，能够大大提高模型的预测性能；

(2)在算法上，相比于EMD分解方法，CEEMD分解方法通过向原序列添加互补的白噪声，一定程度上改善模态混叠现象，同时解决了EEMD分解方法导致的重构误差影响最后预测结果精度的问题，使重构后的误差数量级上保持原有级数，分解性能强；

(3)GRU神经网络具有LSTM的所有优点，即在拟合时间依赖性、非线性的序列保持原有的记忆功能，可以很好地提高模型的预测精度，在算法上大大减小了复杂程度，提高效率，利用Adam算法优化超参数，加快收敛速度和网络性能。通过仿真分析，相比于CEEMD-BP、CEEMD-RNN、GRU预测模型，预测结果更好，后续为电力系统调度提供了预见能力。