基于概率神经网络的直流滤波器电容器开路故障定位方法

李梓玮，许丽娟

(1. 国网四川综合能源服务有限公司， 成都 610072； 2.西南交通大学 电气工程学院， 成都 611756)

0 引 言

在高压直流输电(High Voltage Direct Current，HVDC)系统中，直流滤波器可以滤除换流器在直流侧产生的特征谐波，降低其干扰直流线路附近通信系统、造成直流设备发热和危害系统安全稳定运行等不利影响[1-3]。其中，高压电容器是直流滤波器的重点器件，价格不菲，同时承担着直流侧的大部分电压，容易发生故障[4-5]；低压电容器属于直流滤波器低压调谐区的元件，其故障后将影响滤波性能。当电容器有部分电容元件发生开路故障后，与其并联的正常电容元件流过的电流将增大，进而减少正常电容元件的使用期限，严重时可能会导致雪崩效应，使得更多的电容元件被损害，故应及时对电容器进行检修[6-8]。在HVDC工程中，一般是通过人工逐个测量电容单元的电容值来排查电容器的故障，此种方法的检修效率不高，同时若电容放电不完全，可能会威胁检修人员的安全[9]。因此，有必要研究直流滤波器电容器的开路故障定位方法，提高开路故障检修效率，保证检修人员的安全。

目前，对直流滤波器电容器开路故障定位问题的研究甚少。文献[10]利用不平衡支路电流、直流滤波器首端电流以及两条高压端桥臂支路电流在故障前后的幅值、方向的变化特征，来确定高压电容器的具体故障桥臂。文献[11]提出了一种利用相对电流值来确定电容器组故障位置的方法，采用两条低压端桥臂的支路电流和不平衡支路电流，计算得到两个相对电流值，利用相对电流值的阶跃变化将故障位置定位到高压电容器的具体桥臂。上述方法均较好地实现了高压电容器单个桥臂的开路故障定位，但当高压电容器的2个桥臂同时发生相同的开路故障时，上述方法没有考虑将故障位置定位至2个故障桥臂，同时也均没有考虑低压电容器的开路故障定位。

近年来，深度学习与大数据等新兴技术被广泛应用于故障诊断分类领域。概率神经网络(Probabilistic Neural Network，PNN)是一种融合了密度函数估计和贝叶斯决策理论的智能算法，具有收敛迅速、训练简单、分类准确率高和容错能力强等优点，被广泛应用于模式分类等领域[12-14]。主成分分析法(Principal Component Analysis，PCA)是一种将具有一定相关性的原始变量重新组合成一组新的独立的综合变量的统计方法，其遵循降低数据维度同时数据不失真的宗旨[15-19]。

基于此，文章提出了一种基于概率神经网络的直流滤波器电容器开路故障定位方法。该方法使用归一化和PCA来对样本数据进行缩小量值和降低数据维度处理，在降低问题复杂度的同时，也得到了能有效反映电容器运行状态的特征向量，最后使用PNN对特征向量进行故障分类，从而实现对直流滤波器电容器开路故障的定位。文章利用电容器运行状态样本数据(正常状态、高压电容器4个桥臂分别发生开路故障、高压电容器2个桥臂同时发生相同的开路故障、低压电容器发生开路故障)对所提方法的有效性进行验证，最后考虑电容器的开路故障电容元件数存在差异，以此验证所提方法的适应性。

1 直流滤波器结构和开路故障类型

双调谐直流滤波器具有可以同时滤除2个频率的谐波、占地面积小等优点，被广泛运用于HVDC工程中[20-21]，因此文章对其进行研究。双调谐直流滤波器的结构及开路故障示意图见图1[22]，文中的电容器采用內熔丝结构。其中，H形接线方式的4个电容器组桥臂组成1个高压电容器。高压电容器的等效电容为C1，4个桥臂的等效电容分别为C11、C12、C13、C14，并有C11=C12=C13=C14=C1；低压电容器的等效电容为C2。ih和iw分别为直流滤波器的首端、尾端电流，i1和i2分别为高压电容器C11和C12桥臂的支路电流，iun为不平衡支路电流，ir为电阻器R的支路电流，il2为低压电抗器L2的支路电流。

从图1可知，高压电容器C1的每个桥臂以及低压电容器C2均有64个串联的电容单元，每个电容单元均有60个串并联的电容元件。当有电容元件发生击穿短路故障后，与其并联的正常电容元件将对其进行放电，使得与故障电容元件串联的內熔丝熔断，此时击穿短路故障变化成开路故障[23-25]。图1中F1、F2、F3和F4分别为高压电容器C11、C12、C13和C14桥臂发生开路故障，F5为低压电容器C2发生开路故障。

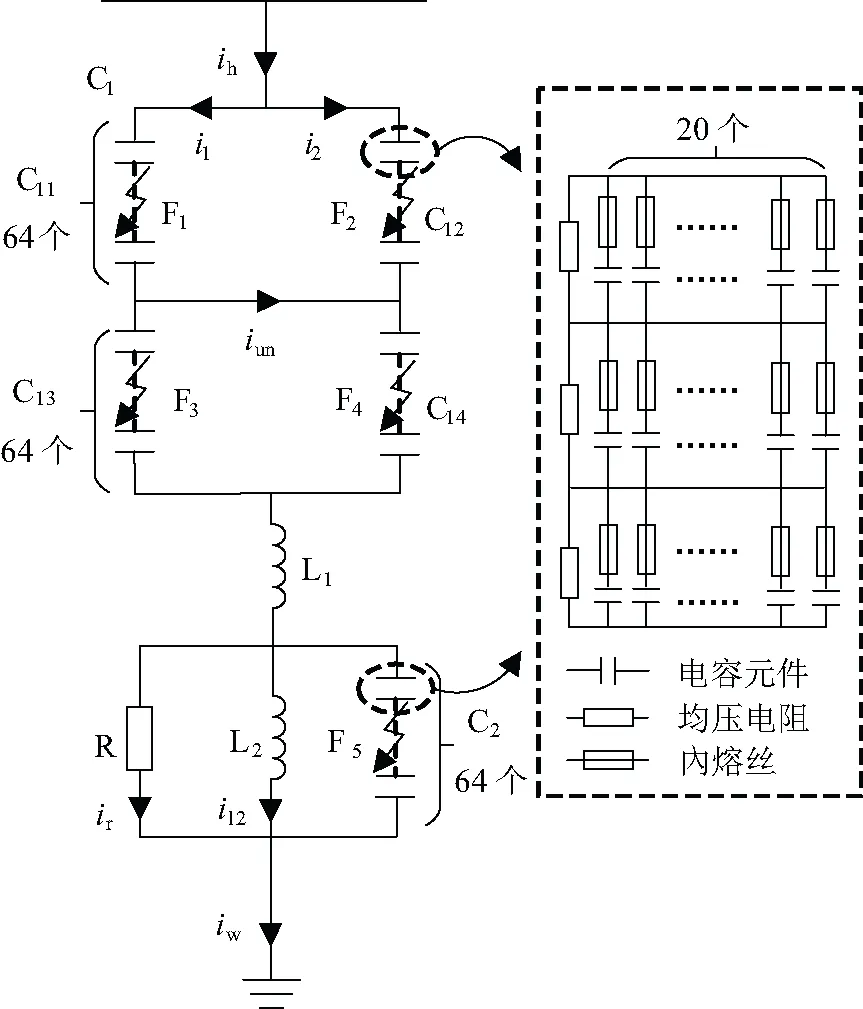
图1 双调谐直流滤波器结构及开路故障示意图

2 直流滤波器电容器开路故障定位方法

2.1 主成分分析法

从多方面研究问题时，会考虑许多与此问题相关的变量，每个变量均在不同程度地体现此问题的信息。在大多数情况下，某些变量是有相关性的，即某些变量反映了一些相同的信息。因此可以使用PCA对变量进行重新组合，然后根据研究问题的需要，选取几个足以反映问题信息的综合变量，从而得到能有效反映直流滤波器电容器运行状态的特征向量，同时也达到了降低数据维度、简化问题复杂性的目的。PCA的计算步骤如下：

假设有n个原始变量A1、A2、…、An，每个原始变量均有m个样本数据，则原始样本数据矩阵A记为：

(1)

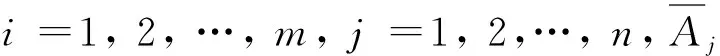
(2)

(3)

(4)

(2)用标准化阵Z求相关系数矩阵M；

(5)

(3)求解特征方程|M-λE|=0，得到n个特征值λj(j=1,2,…n，按从大到小排列)，同时由Mbj=λjbj求解相应的特征向量bj；

(4)求解主成分，Uj为第j主成分；

Uj=Zbj

(6)

(5)求取累计方差贡献率ηΣ(l)，确定主成分个数l。当ηΣ(l)大于95%时，对应的前l个主成分可以反映n个原始变量的大部分信息。

(7)

2.2 概率神经网络

概率神经网络是基于贝叶斯最小风险准则和概率密度函数估计法来进行分类的，是一种由径向基函数发展而来的前向网络，善于进行模式识别。在故障诊断分类方面，其学习方法是前向线性的，分类效率高，训练过程短。概率神经网络一般由四层构成，即输入层、隐含层、求和层和输出层，其基本结构如图2所示。

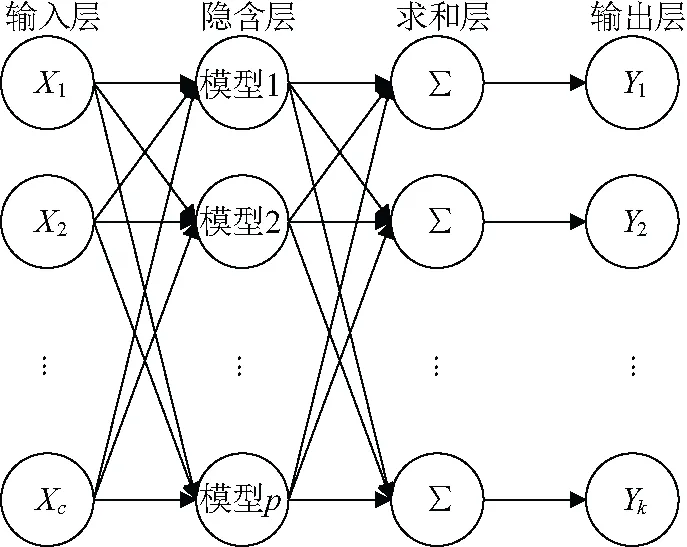
图2 概率神经网络基本结构

在对PNN进行训练时，训练样本的具体处理过程如下所示：

(1)第一层是输入层，负责接收训练样本X，并将其完全不变地传递给隐含层，其中，该层神经元的数量等于输入训练样本X的维数；

(2)第二层隐含层为径向基层，训练样本X的样本个数决定了该层的神经元数量。隐含层中的每个神经元都有一个中心，从输入层接收数据后，计算输入数据到各个中心的距离，每个神经元将输出一个标量，从而计算训练样本X与训练样本中各个分类类别的匹配关系，其输出如式(8)所示：

(8)

式中Wi为输入层和隐含层之间的连接权值，其被设置为各类训练样本;δ为平滑因子；

(3)第三层为求和层，该层的每个神经元代表一个分类类别，神经元数量等于分类类别数量。求和层的每个神经元只与隐含层里同类的径向基神经元建立联系，对同类神经元的概率进行求和，进而得到故障类型概率密度函数估计式，如式(9)所示：

(9)

式中p为训练样本维度;m1为属于分类类别1的训练样本个数;X1i为分类类别1的第i个训练样本。

(4)第四层输出层的每个神经元代表一个分类类别，该层接收求和层的输出，并在其中找到最高概率对应的那个神经元，如式(10)所示，该神经元输出为1，即判断出所测数据属于该神经元对应的分类类别，其余神经元输出为0。最后将输出层的结果乘以向量[1, 2, 3, …,k]′，即乘以每个神经元对应的分类类别数值，进而将输出层的结果转换成分类类别数值。

y=max(f1,f2,…,fk)

(10)

概率神经网络的“训练”是根据输入的训练样本决定网络的神经元数量和连接权值，当PNN中的各参数值确定后训练结束，从而得到训练好的PNN模型。最后将测试样本送入训练好的PNN模型中，实现故障分类。

2.3 基于PNN的电容器开路故障定位方法

基于PNN的直流滤波器电容器开路故障定位流程见图3。

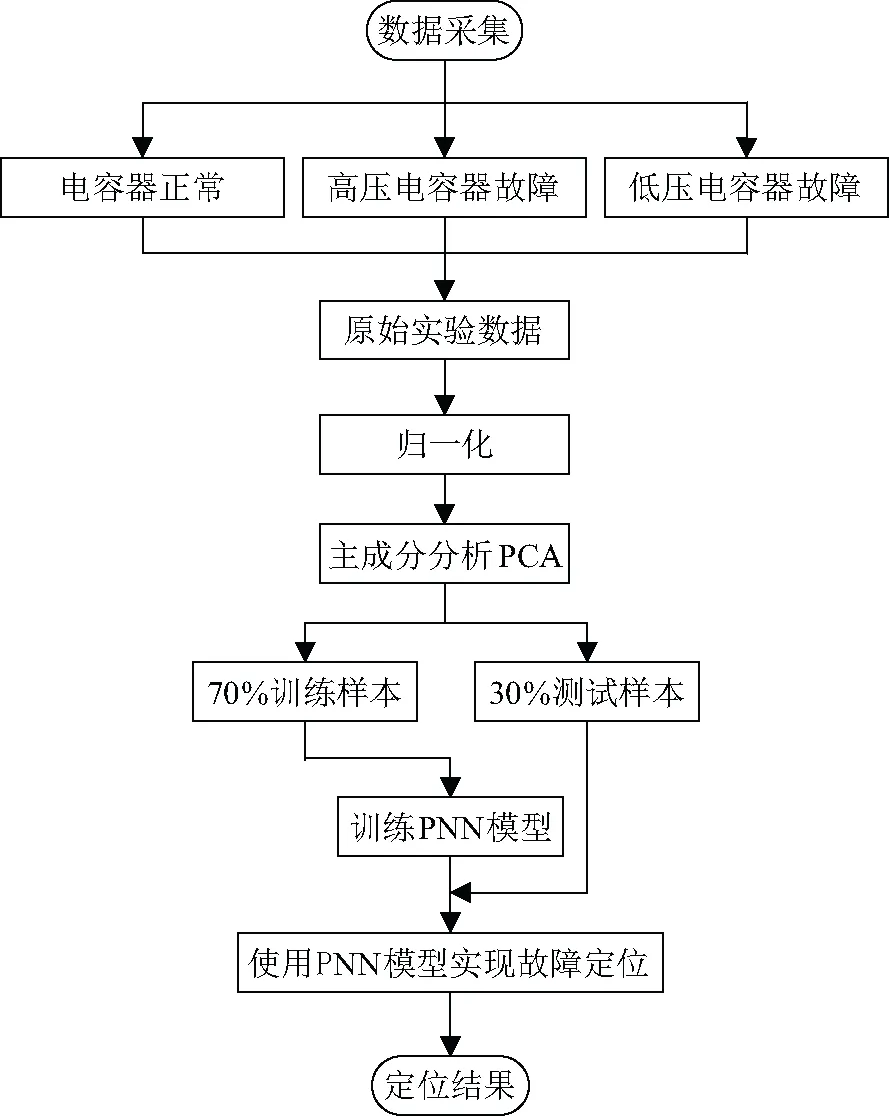
图3 基于PCA-PNN的直流滤波器电容器开路故障定位流程图Fig.3 Flow chart of DC filter capacitor open-circuit fault location based on PCA-PNN

具体步骤如下：

(1)对高压电容器4个桥臂和低压电容器进行开路故障仿真，并借助电流互感器采集电容器处于正常状态和开路故障状态下的原始实验数据；

(2)提取原始实验数据的有效值，再对其进行归一化操作，使数据分布在[0,1]内；

(3)对归一化后的实验数据应用PCA，并选取所需要的主成分，提取关键特征向量；

(4)将经过PCA处理的数据按比例7：3分为训练和测试样本；

(5)将训练样本送入PNN模型，进而得到训练的电容器开路故障定位PNN模型；

(6)将测试样本送入已经训练好的开路故障定位PNN模型中，得到定位结果；

(7)将PNN模型预测的测试样本的定位结果与实际结果作对比，计算定位正确率。

3 实验结果

文章以葛南HVDC工程中的12/24双调谐直流滤波器的结构和参数为例，在PSCAD/EMTDC仿真平台的± 500 kV HVDC系统模型上，对高压电容器的4个桥臂以及低压电容器分别进行开路故障仿真，采集电容器处于正常状态和开路故障状态下的原始实验数据，并用此实验数据验证所提开路故障定位方法的有效性；同时，考虑电容器的开路故障电容元件数存在差异，以此来验证所提开路故障定位方法的适应性。程序在MATLAB R2018b条件下运行，文章所用的双调谐直流滤波器结构如图1所示，参数如表1所示。

表1 双调谐直流滤波器参数

3.1 数据采集

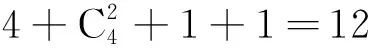
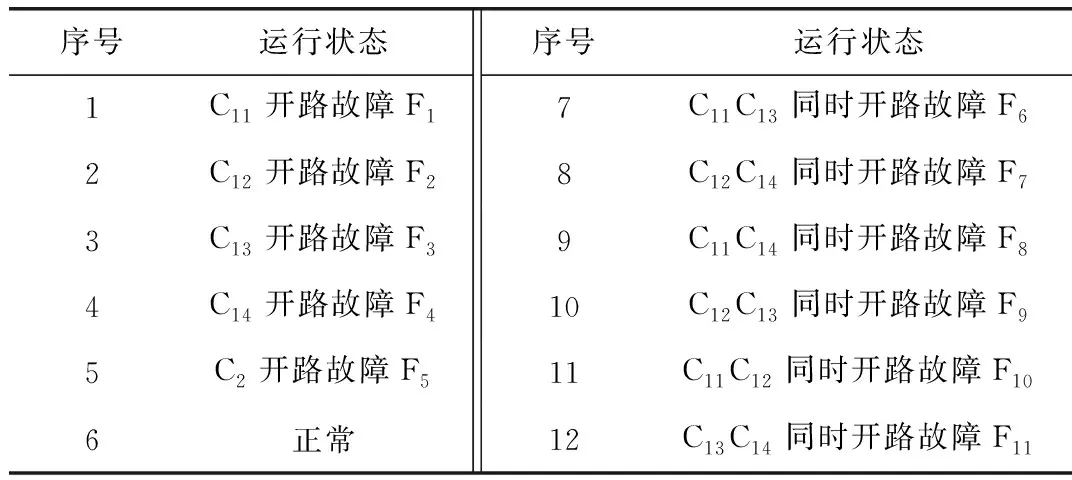
表2 直流滤波器电容器运行状态

3.2 特征提取

监测的直流滤波器变量有：直流滤波器首端电流ih、C11桥臂支路电流i1、C12桥臂支路电流i2、不平衡支路电流iun、直流滤波器尾端电流iw、低压电抗器L2支路电流il2、电阻器R支路电流ir。根据基尔霍夫电流定律，由i1、i2和iun可得到C13桥臂支路电流i3(i3=i1-iun)、C14桥臂支路电流i4(i4=i2+iun)；由iw、il2和ir可得低压电容器C2支路电流ic2(ic2=iw-il2-ir)。因此原始实验数据共有10维，如表3所示。

表3 原始实验数据变量

首先采集原始实验数据的有效值。由于较大的变量值容易覆盖较小的变量值，可能会使信号失真，影响开路故障定位效果，降低开路故障定位准确率，同时为了简化计算、缩小量值，对10维变量作归一化操作，将这10维变量归一化到区间[0,1]。为了删去反映重复的电容器状态数据信息以及不相关的数据信息，使研究问题简单化，对归一化处理后的数据使用PCA。此时样本矩阵有12000×10个数据，首先求取10个变量各自的样本均值和标准差，根据式(2)对样本矩阵作标准化变换，再根据式(5)求取相关系数矩阵，并求取其特征值与特征向量，最后根据式(6)求取各个主成分。文章选取累计方差贡献率大于95%的前几个主成分，PCA降维结果见图4。

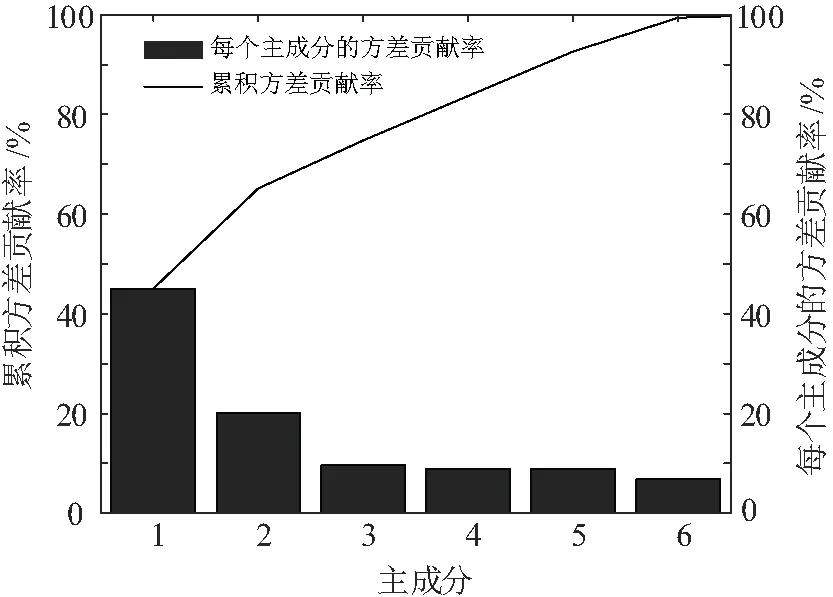
图4 PCA降维结果图

由图4可知，10维变量被降成6维特征向量，即第一、二、三、四、五和六主成分，共有12000×6个数据，且这6个主成分的累积方差贡献率达到了99.390 6%，表明原始10维变量可以用这6个主成分表示。若使用全部的10个主成分，累计方差贡献率达到100%，与前6个主成分的累积方差贡献率仅相差0.609 4 %，故障定位正确率提升不明显，同时还将造成较大的计算量。因此文章采用前6个主成分，其能反映原始变量的绝大部分信息，同时可以降低数据维度、简化计算。这6个主成分中的前3个和后3个主成分的可视化图如图5所示，电容器同一运行状态的数据较为集中，不同运行状态的数据较为分散，若将数据投影到6维的特征空间，不同运行状态数据将变得更加分散，故将其用于接下来的定位过程。

图5 主成分可视化图

3.3 定位结果

通过多次运行程序，在不降低PNN分类正确率的前提下，不断尝试减少训练样本的数量，即减少使用的存储空间和计算时间，最终对直流滤波器电容器的每种故障工况下的每种运行状态均随机选取700组数据作为训练样本，故总训练样本有8 400组数据。将训练样本输入到PNN模型中，设置SPREAD参数值为1.1。此时PNN输入层中有6个神经元，接收6个主成分的数据；隐含层有8 400个神经元，由训练样本的数量决定，该层根据式(8)计算每组训练数据与每个分类类别的匹配程度；求和层有12个神经元，代表电容器运行状态类别数，该层根据式(9)将上一层中属于同一类别的输出进行加权求和；输出层由12个竞争神经元组成，该层接收求和层的输出，并在其中找到最高概率对应的那个神经元，该神经元输出为1，即判断出该组数据属于该神经元对应的电容器运行状态类型，其余神经元输出为0。至此，PNN定位模型训练完成。然后将测试样本送入PNN定位模型中，测试样本的定位结果如图6所示，测试样本的混淆矩阵如表4和表5所示。

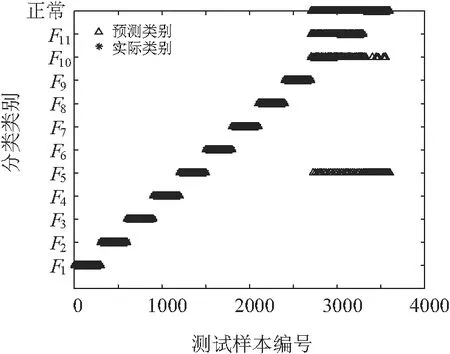
图6 测试样本定位结果

表4 单个支路故障和正常状态测试样本混淆矩阵

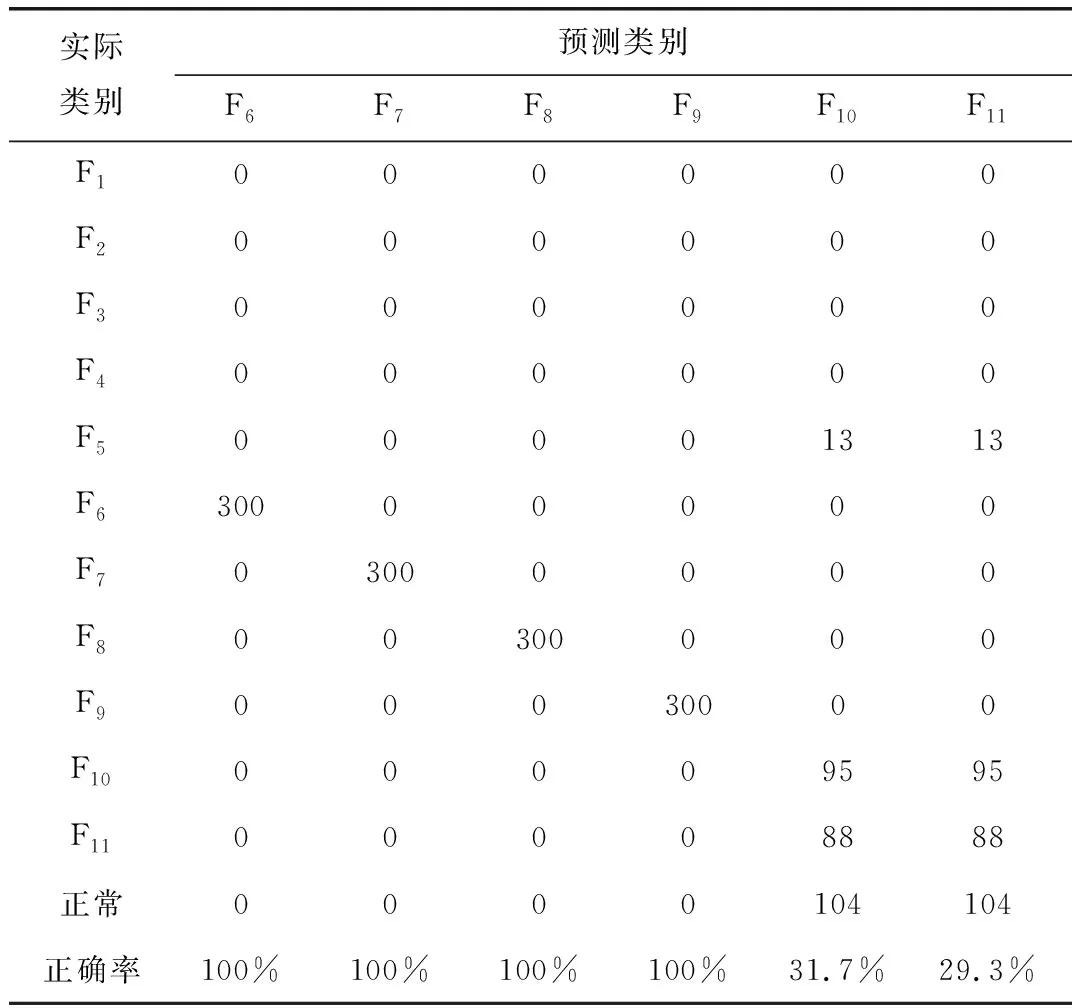
表5 2个桥臂同时故障的测试样本混淆矩阵

由表4、表5和图6可得：(1)对于单个支路发生开路故障，即C11开路故障F1、C12开路故障F2、C13开路故障F3、C14开路故障F4和C2开路故障F5，测试样本定位正确率均为100%；(2)对于电容器处于正常状态，其测试样本定位正确率为88%，其中，分别有8%和4%的测试样本被误判为C2开路故障F5和C11C12同时开路故障F10，其原因为在这3种运行状态中，高压电容器的4个桥臂支路以及不平衡支路的电流特征类似，导致电容器正常状态可能被误判为故障F5、故障F10；(3)对于高压电容器的2个桥臂同时发生相同的开路故障，C11C13同时开路故障F6、C12C14同时开路故障F7、C11C14同时开路故障F8、C12C13同时开路故障F9的测试样本定位正确率均为100%，但C11C12同时开路故障F10、C13C14同时开路故障F11的测试样本定位正确率很低，只有31.7%和29.3%。因此文章所提方法可有效定位除了F10和F11这两种运行状态之外的10种运行状态。

当直流滤波器电容器处于正常状态时，由于C11=C12=C13=C14，4个桥臂的等效阻抗相等，因此流过高压电容器4个桥臂的电流均相等，同时不平衡支路电流为0。当C11和C12桥臂同时发生相同的开路故障时，依然有C11=C12，这2个桥臂的等效阻抗依然相等，故流过C11和C12桥臂的2个电流相等，且此时C13和C14桥臂处于正常状态，有C13=C14，故流过C13和C14桥臂的2个电流相等，且等于流过C11和C12桥臂的2个电流，同时不平衡支路电流为0。同理，当C13和C14桥臂同时发生相同的开路故障时，流过高压电容器4个桥臂的电流均相等，同时不平衡支路电流为0。此外，在上述3种运行状态中，低压电容器C2均无故障，低压调谐区的电流故障特征有相似之处。因此，故障F10、故障F11和正常状态的部分故障特征较相似，故障F10和F11易被错误分类，导致其定位正确率低。故文章所提方法不考虑故障F10和F11这两种运行状态。

3.4 开路故障电容元件数量对定位结果的影响

为验证基于PNN的直流滤波器电容器开路故障定位方法的适应性，考虑电容器的开路故障电容元件数存在差异。以电容器有2个串联和15个并联的电容元件发生开路故障；3个串联和15个并联的电容元件发生开路故障；3个串联和18个并联的电容元件发生开路故障为例，对电容器分别进行开路故障仿真。对上述3种故障工况，按照文章3.1节所述过程分别采集样本数据，按照图3所示流程对数据进行提取有效值、归一化和PCA处理后，对每一种故障工况下的每一种运行状态均随机选取700组数据作为训练样本，训练样本包含了不同故障工况下的不同运行状态的数据；将每一种故障工况下的每一种运行状态的其余300组数据作为测试样本，故总训练样本有21 000组，总测试样本有9 000组。测试样本的定位正确率如表6所示。

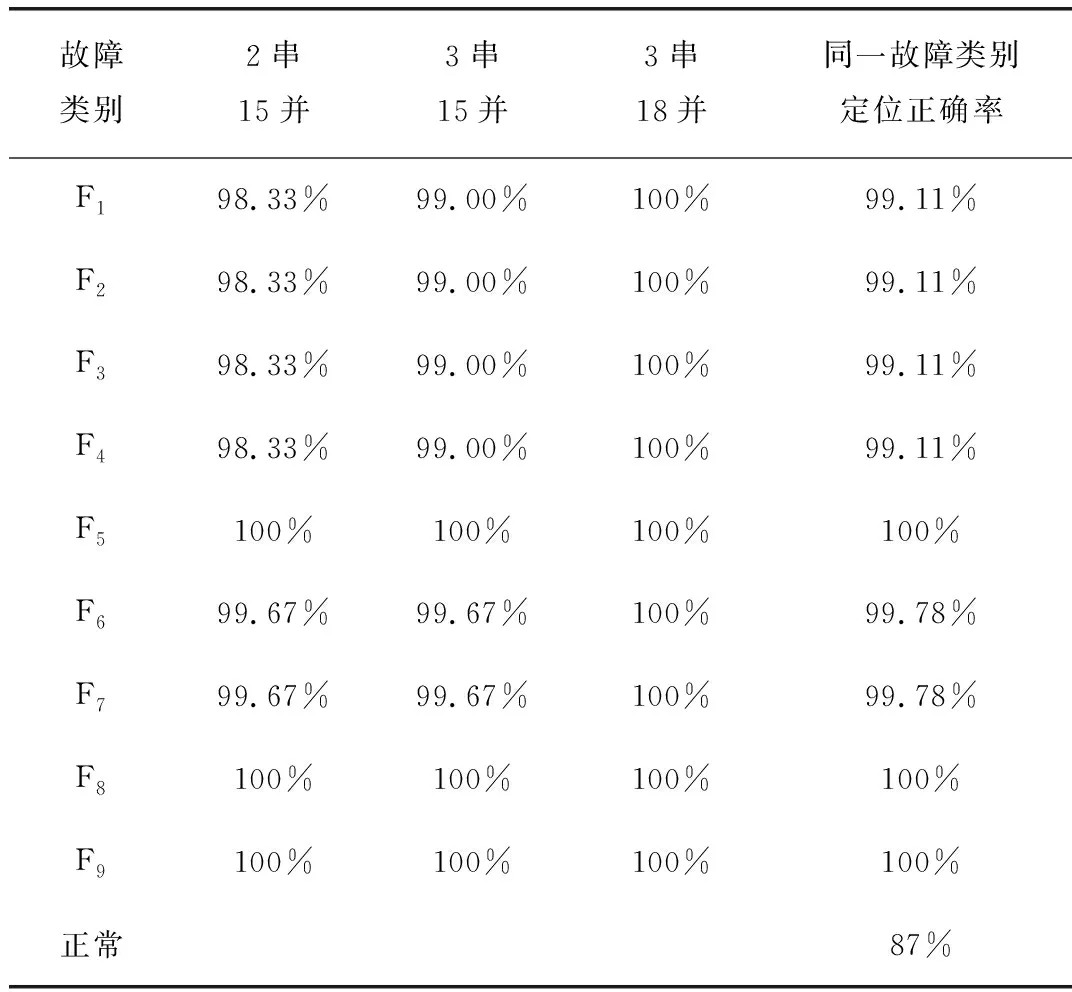
表6 不同数量故障电容元件测试样本定位正确率

由表6可知，直流滤波器电容器发生开路故障的电容元件越多，文章所提方法的故障定位正确率越高。若故障电容元件数较少，可能会导致其故障特征不明显，从而使得故障定位正确率降低，而在实际HVDC工程中，只有当故障电容元件达到了一定数量，才会对其进行检修。因此，当电容器的开路故障电容元件数存在差异时，文章所提方法可以有效定位故障位置。故文章所提基于主成分分析法和概率神经网络的直流滤波器电容器开路故障定位方法具有较高的适应性。

4 结束语

文章对直流滤波器电容器开路故障定位问题进行研究，提出了一种基于主成分分析法和概率神经网络的电容器开路故障定位方法，得到以下结论：

(1)采用主成分分析法对已作归一化处理的样本数据进行降维操作，将原始的10维变量降为6维特征向量，累计方差贡献率达到了99.390 6 %，因此，可用6维特征向量代表原始10维变量；

(2)利用训练样本训练PNN模型，然后利用测试样本预测PNN模型的定位结果。电容器状态样本数据的定位结果表明：所提方法可有效识别高压电容器C11开路故障F1、C12开路故障F2、C13开路故障F3、C14开路故障F4、低压电容器C2开路故障F5、高压电容器C11C13同时开路故障F6、C12C14同时开路故障F7、C11C14同时开路故障F8、C12C13同时开路故障F9和电容器正常状态共10种运行状态；

(3)考虑电容器的开路故障电容元件数存在差异，以2个串联和15个并联等3种不同组合的电容元件发生开路故障为例，验证所提定位方法的适应性，定位结果表明，测试样本中不同运行状态的定位正确率分别为99.11%、 99.11%、 99.11%、 99.11% 、 100%、 99.78%、 99.78%、 100%、100%和87%，定位正确率较高，因此所提方法可有效定位到电容器的故障位置，具有较高的适应性。