基于改进Benders分解的配电网扩展规划机会约束优化方法

2023-01-18闫明文刘惠颖宫游李兴刚文茹馨廖小兵

电测与仪表 2023年1期

闫明文，刘惠颖，宫游，李兴刚，文茹馨，廖小兵

(1. 国网黑龙江省电力有限公司供电服务中心, 哈尔滨 150000; 2.武汉工程大学电气信息学院, 武汉430205)

0 引言

配电网位于电力系统的末端，起着连接电力系统和用户并分配电能的作用，是保障电力可靠供应的关键环节[1]。一方面，随着经济、社会水平的发展导致负荷水平急剧增长;另一方面，基于分布式风电、分布式光伏的分布式电源(Distributed Generation，DG)大量的分散接入，其出力的随机性、波动性导致配电网的运行方式更加复杂多变。在此背景下，配电网为了适应负荷水平的发展，一方面需要进行变电站、配电线路的扩展规划[2]，另一方面在规划过程中需要考虑到分布式电源出力的不确定性[3]。

近年来，为了适应负荷水平增长和DG分散接入，配电网规划研究从早期的网架规划发展到源网荷储的多维协调规划。文献[4]考虑了不同的DG类型和负荷类型，研究了源荷协调规划方法。文献[5]将电池储能和分布式电源同时嵌入到配电网规划模型中，提出了配电网规划-运行联合优化模型。文献[6]在配电网规划中将电动汽车作为充电负荷，可以通过充电负荷转移高峰负荷成本，降低了规划期内的建设成本。文献[7]进一步将基于风光可再生能源的风光储充电站嵌入到配电网规划中，建立了配电网双层规划模型。文献[4-7]是从源网荷储协调规划的角度建立完善的配电网规划模型，但缺乏对DG出力不确定性的考虑。

迄今为止，为了解决DG出力的不确定性，已有研究提出了随机规划方法[8]、鲁棒规划方法[9-10]、机会约束规划方法[11]。配电网随机规划方法根据DG出力的概率密度函数生成大量的离散场景集，接着进行场景削减来获取少量的典型场景集，基于削减场景的随机优化方法虽然维持了确定性规划模型，简单易于实现，但典型场景的代表性和全局性难以获得精确可靠的规划方案[12]。而配电网鲁棒规划为了克服随机规划的弊端，通过在DG出力的区间范围内寻求最恶劣场景下的规划结果，其规划结果往往偏保守。机会约束规划方法是允许规划模型中不等式约束成立的概率不小于某一置信水平，可以避免一些极端恶劣场景下造成配电网规划投资的浪费，这也是机会约束规划方法与随机规划方法、鲁棒规划方法的最大优势。文献[13]建立了综合设备购置成本、安装成本、运行维护成本、系统运行成本以及残值回收的全寿命周期成本模型，考虑了电压和传输容量成立的机会约束，并采用改进人工鱼群算法求解，但智能算法固有的收敛性差难以得到全局最优解。文献[14]考虑了电动汽车大量接入的场景，提出了基于蒙特卡洛模拟的配电网两阶段场景规划方法，但场景数会随着配电网维数增大而急剧增加。文献[15]提出了输电网和配电网一体化的规划思路，为了克服场景法和优化维数的问题，提出了分布式求解思路。文献[16]面向含高比例可再生能源的主动配电网，提出了一种基于典型场景的软开关机会约束规划方法。从文献[14-16]中不难看出，已有的机会约束方法都是基于场景法，其计算效率与场景数之间的矛盾一直制约机会约束优化方法的应用。

为了解决已有配电网机会约束规划方法的不足，提出了基于双线性Benders分解的配电网扩展规划两阶段机会约束优化方法，在第一阶段优化投资成本，在扩建线路、变电站增容和电容器组进行投资优化；在第二阶段优化运行成本，并通过场景数对负荷需求和电价不确定性进行建模，构建了基于场景的配电网随机扩展规划模型，为了进一步提高优化效率，设计了基于双线性Benders分解的机会约束优化方法。三个测试算例验证了所提出方法的优越性。

1 配电网随机扩展规划模型

首先建立配电网扩展规划的两阶段优化模型，其中第一阶段在规划层面决策变电站扩建、输电线扩建和电容器配置；第二阶段考虑扩建后的新系统在运行层面进行决策。由于第二阶段扩建系统的优化运行是根据随机负荷和实时电价进行的，采用随机优化中的场景法来建立配电网扩展规划模型，以一组离散场景和概率来表征不确定性。

1.1 目标函数

配电网扩展规划的目标是使得投资成本Cinv和运行维护成本Copr,s最小，其中投资成本Cinv包括变电站、馈线线路和电容器组投资的固定成本和可变成本；运行维护成本Copr,s包括切负荷惩罚成本、网损成本和馈线运行维护成本。因此，所建立的配电网扩展规划的目标函数用式(1)描述如下：

(1)

其中:

(2)

(3)

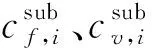
1.2 约束条件

配电网扩展规划模型的约束条件包括系统的功率平衡约束、变电站节点功率约束、馈线电流约束、节点电压约束、支路潮流约束、变电站容量约束、0-1决策变量约束、变电站和电容器组投资约束、辐射状网络约束、扩建馈线电流约束。下面将逐一介绍。

(1)节点功率平衡约束。

(4)

(5)

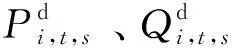
(2) 变电站节点功率约束。

(6)

(7)

(3) 馈线电流约束。

(8)

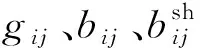
(4)节点电压约束。

(9)

(10)

(11)

(12)

(13)

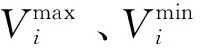
(14)

(15)

(16)

(17)

(18)

式(14)是由辅助变量Rij,t,s和Lij,t,s构成的二阶锥约束，具体定义见式(15)～式(16)。各支路的实际有功功率和无功功率分别由式(17)、式(18)约束。

(6) 变电站容量约束。

(7)变电站和电容器组投资约束。

(20)

(21)

式中M为一个足够大的数。

(8)0-1决策变量约束。

(22)

(23)

(24)

式(22)～式(24)表明，如果对现有馈线进行投资(即kij=1)，考虑到网络拓扑的辐射性要求，旧的馈线必须从网络断开(即yij=0)。

(9)辐射状网络约束。

(25)

(26)

(27)

(10)扩建馈线电流约束。

(28)

(29)

上述建立的基于场景的配电网扩展规划模型是一个大规模的混合整数二阶锥规划模型(Mixed Integer Second Order Cone Programming，MISOCP)。虽然商业求解器能求解，但随着配电网的规模和情景数的增加，优化效率需要进一步的提升。

为了便于推导，本节将建立的基于场景的随机规划模型表示矢量形式，定义：

(30)

(31)

式中x表示第一阶段规划层面的投资决策变量；y表示第二阶段运行层面的操作决策变量。使用下标表示场景s中的相关参数(gs,Es,ds,Bs,ls,Hs,hs)，因此，配电网扩展规划的基于场景的随机优化模型(StoP)可表示为：

(32)

s.t.Fx≤f

(33)

Esys=ds， ∀s

(34)

Ax+Bsys≥ls， ∀s

(35)

(36)

与第1节建立的基于场景的随机规划模型相比，式(33)为投资决策变量约束，式(34)为功率平衡方程约束，式(35)为投资和运行耦合的决策约束，式(36)为二阶锥约束。

2 基于双线性Benders分解的机会约束MISOCP模型求解方法

2.1 基于Big-M的机会约束MISOCP模型求解方法

在第1节建立的随机规划模型StoP可以采用Big-M将其转化为机会约束规划模型(CC-bigM)，如下所示：

mincx+G(y1,ω1,…,y|S|,ω|S|)

(37)

s.t.Fx≤f

(38)

Esys-ds+Mωs≥0, ∀s

(39)

ds-Esys+Mωs≥0, ∀s

(40)

Ax+Bsys+Mωs≥ls, ∀s

(41)

‖Hsys‖-Mωs≤hsys, ∀s

(42)

(43)

ωs∈{0,1}， ∀s∈S

(44)

显然，如果ωs=1，含场景s中的所有约束均不起作用，可以忽略。因此，0-1变量ωs可以用来反映在获得最优解时包含的场景s。根据式(43)，寻求一个性能良好的规划解满足在所有随机场景中成立的概率不低于(1-ε)×100%，因此，这种机会约束规划方法忽略了一些场景，在目标函数式(37)中引入了含场景s和ωs的函数G，以获取第二阶段决策的成本贡献。

2.2 基于双线性Benders分解的机会约束MISOCP模型求解

虽然2.1节介绍的基于Big-M的机会约束MISOCP模型求解方法将配电网扩展规划模型转化为一个混合整数二阶锥规划问题，但由于场景数多导致其计算量仍然很大。由于机会约束优化方法仅关心相关场景中产生的成本，因此，通过推广Benders分解，提出了基于双线性Benders分解的机会约束(CC-BL)MISOCP模型求解方法，比基于Big-M的机会约束MISOCP模型求解方法具有更好的优化性能[19]，具体如下所示：

(45)

s.t.Fx≤f

(46)

ηs=gsys(1-ωs), ∀s

(47)

(Esys-ds)(1-ωs)=0, ∀s

(48)

(Ax+Bsys-ls)(1-ωs)≥0， ∀s

(49)

(‖Hsys‖-hsys)(1-ωs)≤0， ∀s

(50)

(51)

ωs∈{0,1}, ∀s

(52)

注意式(47)中如果ωs=1，即忽略场景s，它不会影响总成本。因此，通过将ωs赋值为1或0，情景s的影响将全部反映在目标函数中。此外，当ε=0，对于所有场景s∈S，则有ωs=0，这将CC-bigM或CC-BL模型简化为相应的StoP模型。因此，StoP模型作为CC-bigM或CC-BL模型的特例。

Benders分解是一种主子问题结构化方法，但目前主要应用于鲁棒优化模型，很少有将这一方法扩展应用到随机MISOCP或者机会约束MISOCP模型。因此，将扩展Benders分解应用于机会约束机MISOCP模型。下面将介绍双线性Benders分解的子主问题和迭代过程[20]。

2.3 子问题和主问题

(53)

s.t.Esλs+Bsθs+Hsσs+μshs=gs

(54)

‖σs‖≤μs

(55)

θs,μs≥0,λs,σs任意

(56)

式中θs、μs、λs、σs为对偶变量。

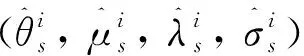
(57)

s.t.Fx≤f

(58)

(59)

(60)

ωs∈{0,1}，s∈S

(61)

可以看出：通过列举SPs的所有极值点，MP-BL就是CC-BL精确的Benders重构模型。因此，MP-BL本质上是在一个极值点处松弛的CC-BL，其最优值为一个下界。此外，式(59)中的双线性项可以使用McCormick线性化，从而将MP-BL转换为混合整数线性规划问题求解。具体算法流程图如图1所示。

3 仿真分析

将通过一个简单的示例和两个复杂的配电系统来验证所提出方法的优点。采用MATLAB 2018b编程实现文中的算法，其中误差容许度e为0.1%，并在默认设置下采用商业求解器Mosek[21]求解MISOCP模型。

为了便于说明，先将所提出的方法应用于图1所示的简单示例中。这个配电系统将在第五年进行扩建，负荷数据如表1所示。假设变电站的固定和可变投资成本分别为20万$和5万$/MW。假设馈线投资和维护成本分别为15万$/km和450 $。电容器组固定和可变投资成本分别为3000 $、 450 $/kvar。年化成本使用r(1+r)y/[(1+r)y-1]计算，其中r为利率，y为年数，这里以15年的投资回报期以10%的利率考虑。假设网损成本是表1给出的价格的10倍。设置7条馈线作为候选线路包括替换现有的线路和新的候选线路5-4和3-5。

图1 双线性Benders分解法求解流程图

表1 负荷数据及其电价

(1)不采用机会约束案例分析：本节设置了三种案例，一种是确定性案例(记为案例0)，另一种是两种随机性案例(记为案例1和案例2)，考虑负荷需求和电价的不确定性，采用均匀分布得到10个等可能性的场景，其中负荷需求和电价根据表2中的数据进行缩放，比例因子是从[0.5, 3]区间独立生成的随机数，优化得到的配电网扩建结果如图2所示。案例0不需要投资，仅通过移除馈线3-4实现辐射状拓扑。案例1的结果表明，将现有的2个支路1-2和2-5支路替换为容量更大的支路，变电站增容了0.116 p.u.。案例1也不需要投资，删除现有分支2-4以增加辐射性。

图2 原网络和扩建网络示意图

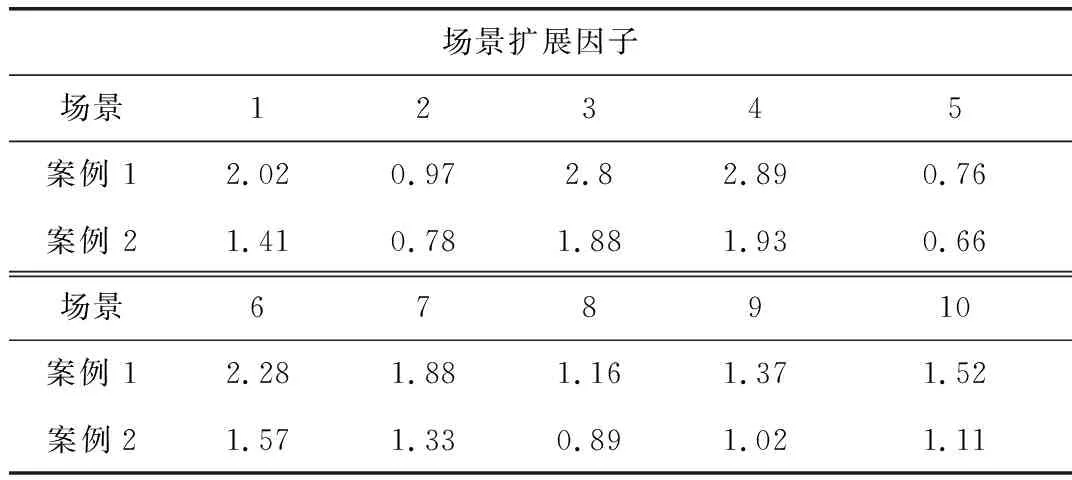
表2 随机场景数据

(2)机会约束案例分析：对表2中案例1所描述的情景采用机会约束模型进行求解，得到机会约束水平分别为100%、90%、80%、65%的规划结果如表3所示。对于这个小系统，得到的规划结果与图1中案例1基本上相似。观察最昂贵成本的场景，即4、3、6(见表2)，随着机会约束水平的降低而下降。因此，通过调整机会约束水平，决策者可以在扩建成本和期望的安全风险之间进行权衡。

表3 不同机会约束水平规划结果对比

(3)优化性能分析：表4比较了三种不同优化方法的优化性能。如果由于程序运行时间超过1 h不能得到最优解，结果被标记为“T”。三种优化方法依次是基于商业求解器Mosek求解(直接求解Stop模型)、基于Big-M的随机规划方法(CC-bigM)、基于双线性Benders分解的机会约束规划方法(CC-BL)。

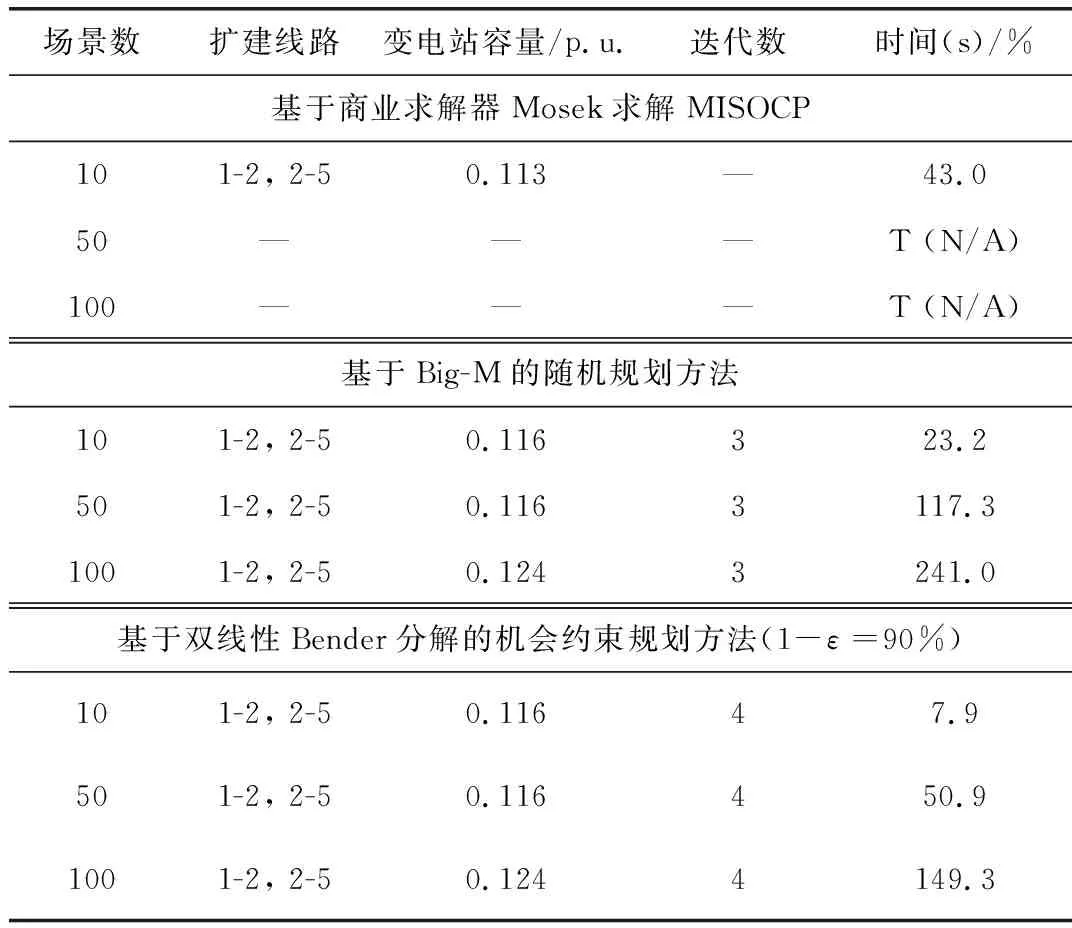
表4 不同优化方法规划结果对比

从表4中可以看出：即使是商业求解器Mosek也不能在1 h内求解5节点系统。反观，基于Big-M的随机规划方法和基于双线性Benders分解的机会约束规划方法的优化效率大大提高，将优化时间减少了几个数量级。具体而言，基于双线性Benders分解的机会约束规划方法虽然比基于Big-M的随机规划方法多迭代了1次，但由于在迭代子问题中的优化维数更低，因而优化时间更快。

第二个测试系统是在18节点配电系统[22]的基础上进行了一些修改，如图3所示，该系统有18个节点、2个变电站、24条支路。现有和候选线路如表5所示。电价和负荷需求的场景同样采用均匀分布得到20个等可能性场景，比例因子均匀分布在[0.6,1.8]区间，其他设置与5节点系统相同。

设置3种情况：(1)负荷水平为150%的确定性情况；(2)两种随机情况，机会约束水平分别为100%和80%。18节点配电系统扩展规划结果如表5和图3所示。由表5可以看出：随机情况下需要投资9条新馈线扩建电网，变电站扩建2.84 MV·A，而在确定性情况下不增加变电站容量。很显然，不同的辐射状拓扑结构对应着不同的成本，而最高的扩建成本一定是在100%的机会约束水平下得到的，这是由于其要求所有场景下安全性约束都要满足。

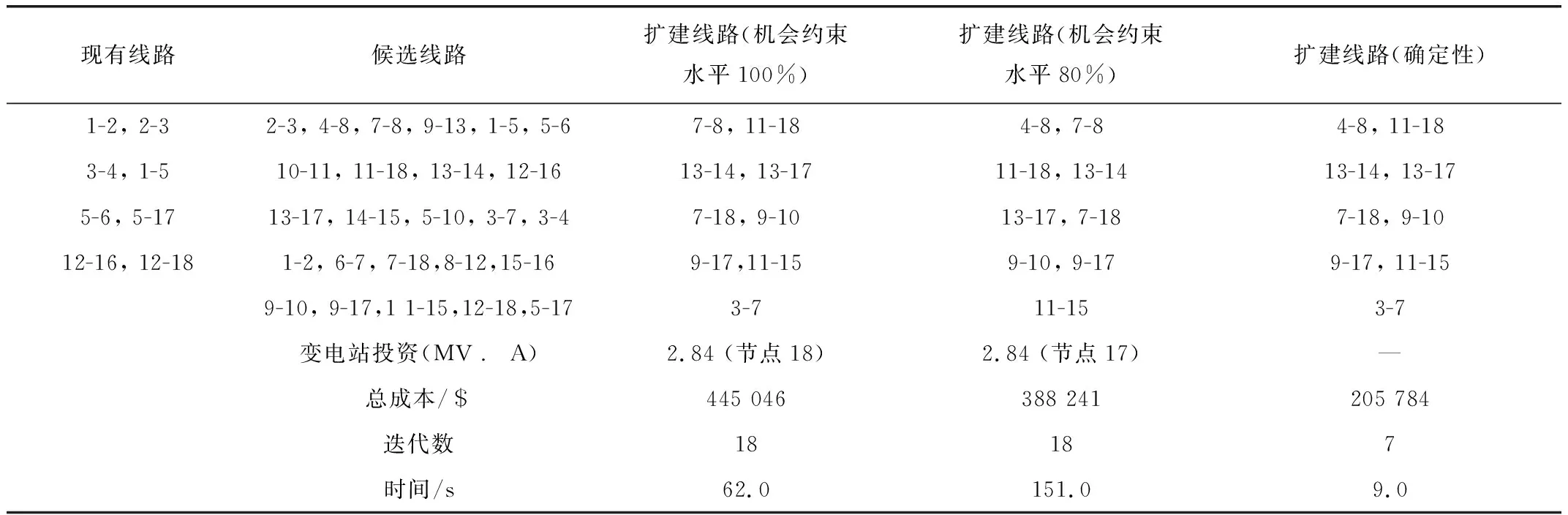
表5 18节点配电系统扩展规划结果

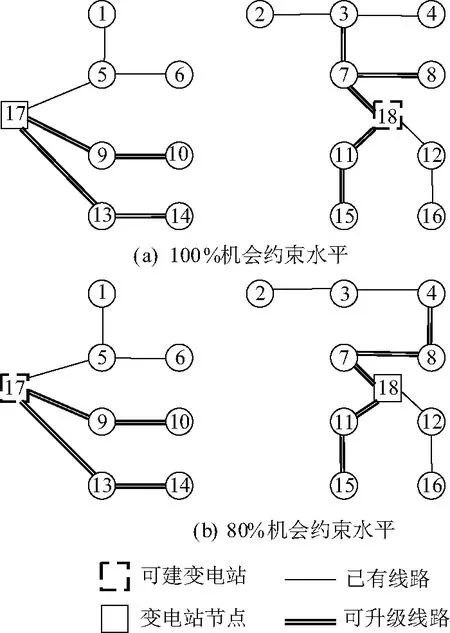
图3 配电网扩展规划结果

第二个测试系统是在138节点配电系统的基础上进行了一些修改，该系统由138个节点、3个变电站和151条线路组成。负荷的无功功率是在功率因数固定为0.96的情况下计算得到的。设置49条候选馈线，电价和负荷需求的场景同样采用均匀分布得到50个等可能性场景，比例因子均匀分布在[0.85, 1.5]区间，其他设置与18节点系统相同。

所提出的方法能在在5小时内获得优化结果，如表6所示。表6中给出中场景数为1的结果是确定性场景，这是为了对比所提出的方法。显然，由于138节点系统规模较18节点系统更大，优化时间比18节点系统要长得多。然而，对比表5和表6的结果可以看出：所需的迭代数并没有明显的增加，这表明所提出的基于双线性Benders分解的机会约束规划方法具有很强的鲁棒性，收敛性较好。