凝灰岩碎石回弹模量影响规律

2023-01-18孙甲乾赵小春卫奥忠余祥晶王旭昊

土木工程与管理学报 2022年6期

李程，孙甲乾，王曈，赵小春，卫奥忠，余祥晶，王旭昊

(1. 长安大学公路学院，陕西西安 710064; 2. 西藏天路股份有限公司, 西藏拉萨 850000;3. 交通运输部科学研究院, 北京 100029； 4. 交科院公路工程科技(北京)有限公司, 北京 100088；5. 镇江市交通运输局综合交通事业发展中心, 江苏镇江 212004)

路面基层材料的回弹模量最初由Seed等[1]于1962年提出，定义为瞬时脉冲荷载峰值与回弹应变之比，用来表征路面结构层的刚度特性，并被沥青混凝土路面力学-经验法(MEPDG)[2]定为粒料基层路面结构设计的唯一力学输入参数。粒料回弹模量不仅受材料自身性质影响(母岩强度、材料级配、颗粒形态等)，试验条件(应力水平、加载时长、加载次数等)也会对材料的测试结果产生影响[3～14]。

王随原[11]发现碎石粒料回弹模量与围压呈正相关的变化趋势；且围压能明显制约轴向偏应力对于粒料类材料回弹模量的影响，低围压情况下轴向偏应力对于模量的影响比高围压情况下大[10]。有研究表明粒料在低围压的情况下(<30 kPa)，试件的粗颗粒会在轴向偏应力作用下发生显著破碎，导致级配和颗粒形态发生改变，回弹模量显著降低[13]。Lackenby等[14]发现了循环偏应力对应围压的最佳范围(230 kPa偏应力对应15～65 kPa的最佳围压，750 kPa偏应力对应50～140 kPa的最佳围压)，保证应力水平在最佳范围内能够有效降低粒料在试验过程中产生的颗粒破碎。

与此同时，粒料类材料的级配对于路面基层的回弹模量和永久应变有着更为严重的影响。Mishra和Tutumluer[8]发现当公称粒径在0～0.075 mm之间的颗粒含量从4%上涨到16%时，模量值下降了20%～25%。Barksdale[4]选用了3种不同的粒料进行回弹模量试验，结果显示随着细颗粒含量的增加，回弹模量降低了60%左右。美国陆军工程科的科研人员早在20世纪60年代就观察到路用碎石材料在施工压实后产生了严重的颗粒破碎和级配退化，造成所铺筑的基层回弹模量减半，永久变形增加1～3倍之多，极大地缩短了沥青路面使用寿命[12]。

目前，确定路面基层材料回弹模量的方法一般有3种：现场原位试验反算、室内重复加载三轴压缩试验、回弹模量预测模型。相比于工作量大、成本高的现场试验和操作复杂、设备昂贵的室内试验，预测模型因其便捷性被广泛应用。国内外研究人员[15～26]提出了一些考虑应力水平及湿度的粒料回弹模量Mr预测模型，表1汇总了现有回弹模量预测模型。我国发布的JTG D50—2017

表1 现有常用回弹模量预测模型

《沥青路面设计规范》采用了美国国家公路合作研究项目“沥青路面设计中的回弹模量试验确定方法(NCHRP 1-28A)”提出的三参数本构模型表征材料模量的应力依赖特点。

国内外学者[15,21]通过对修正的k-θ模型、修正UZAN模型以及NCHRP 1-28A模型对比发现，修正k-θ模型只设置了体应力作为应力变量，不能独立反映轴向偏应力和围压对于回弹模量的影响，且忽略了试验过程中产生的剪切应力。修正UZAN模型在修正k-θ模型的基础上加入了轴向偏应力作为第2个应力变量，但在模量计算过程中出现了不定值问题，且仍未考虑剪应力的影响。NCHRP 1-28A模型在修正UZAN模型基础上使用八面体剪应力来替代轴向偏应力作为第2个应力变量，从而使得该类预测模型能够同时反映体应力、偏应力以及剪切强度的影响，更好的表征粒料基层刚度和抗变形能力，为路面结构组合设计、层厚计算提供更为准确的设计参数。NI模型在修正UZAN模型和NCHRP 1-28A模型的基础上，使用轴向偏应力和围压应力作为应力变量，虽然不能反映剪切作用，但能够更加独立地反映基层单元的三相受力状态，且消除了模量不定值问题[16]。另有学者[22,23]引入基质吸力到现有预测模型中，来反映湿度和应力水平对于回弹模量的综合影响。总结现有国内外粒料类基层材料回弹模量预测模型发现，现有预测模型仅考虑了应力水平或湿度，尚未考虑粒料级配这一重要影响因素。

因此，本文选取一种凝灰岩碎石粒料，采用AASHTO T-307粒料回弹模量试验方法开展室内试验，探究了集料级配和应力水平对粒料回弹模量的影响规律，并基于试验数据对3种典型回弹模量预测模型进行拟合分析，使用预测效果最佳的NCHRP 1-28A模型建立级配指数n与回归参数k1，k2，k3的关系式，定量评估集料级配对于回弹模量的影响。

1 级配设计与压实特性

1.1 原材料基本物理性能

本文选取甘肃临洮地区的一种凝灰岩碎石集料进行试验。表2为该材料6种不同粒径范围的物理参数及压碎值。该凝灰岩碎石表观密度ρa在2.753～2.816 g/cm3之间，内部闭口空隙小。

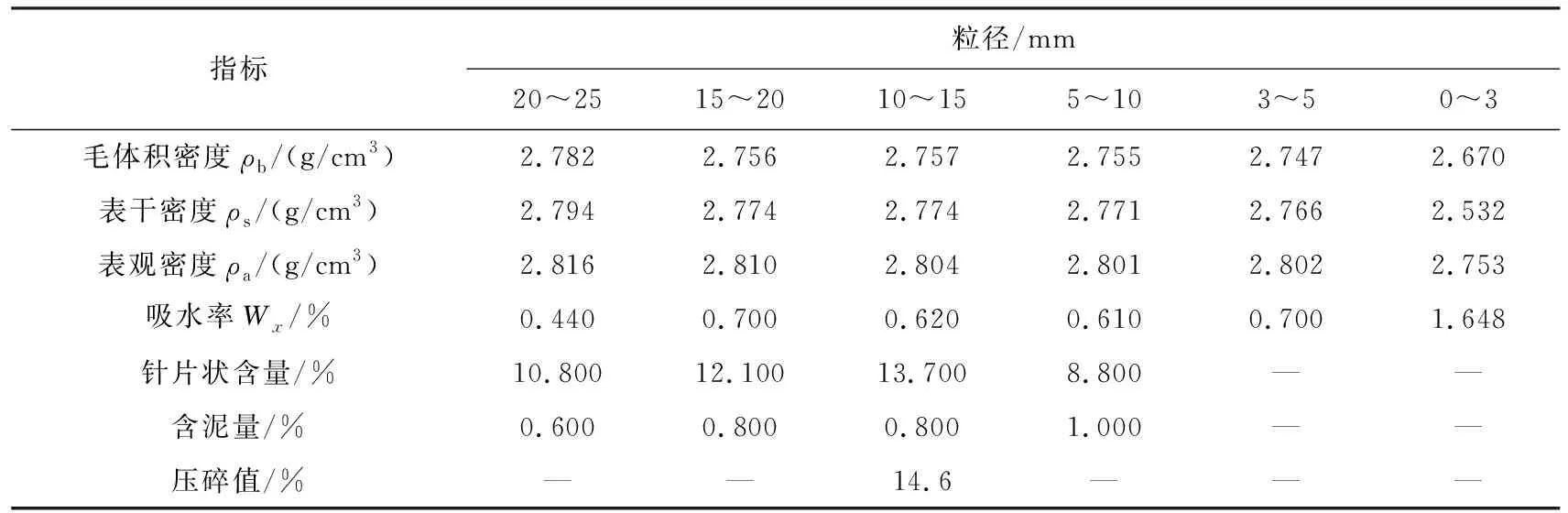
表2 6种不同粒径范围的集料样本物理参数及压碎值

1.2 目标级配设计

本文将集料样本按照《公路工程集料试验规程》筛分成9档，采用泰波公式[28]设计目标级配，最大粒径为19 mm，使用级配指数n对试件级配作定量化设计(式(1))，并用于级配影响规律的统计分析。共设计7组目标级配(n取0.3，0.35，0.4，0.45，0.5，0.55，0.6)。

(1)

式中：p为某一等级粒径通过率(%)；d为粒料颗粒粒径(mm)；D为级配碎石最大粒径(mm)。

图1汇总了泰波公式计算的7组目标级配曲线，0.075 mm以下颗粒占比在3.6%～19.0%之间。

图1 本文所设计的7种目标级配曲线

1.3 最大干密度与最佳含水率

按照JTG E51—2009《公路工程无机结合料稳定材料试验规程》中规定的振动压实试验确定7个目标级配碎石最大干密度和最佳含水率。选定0，2%，4%，6%，8%共计5个含水率进行试验。

图2展示了7组不同目标级配混合料的干密度随含水率变化情况。当含水率在0～2%时，干密度出现最小值，且随着含水率的增加而呈现先减小后增大的趋势。产生此现象的原因是材料在较干燥情况下，颗粒滑移会受到空隙内少量水分的虹吸力影响[10]。因此，本文建议选用此种材料在铺筑柔性基层时，材料的含水率应大于2%。

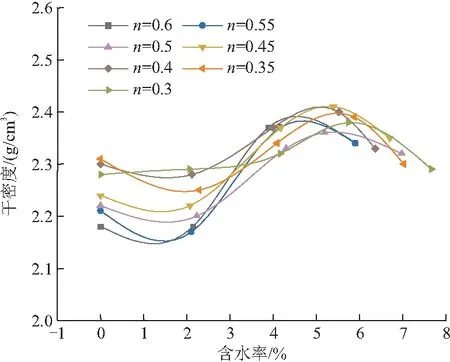
图2 7种目标级配碎石干密度随含水率变化曲线

图3展示了7组目标级配试件最佳含水率和最大干密度随级配指数n变化的曲线。当n取0.45时(0.075 mm以下颗粒含量占比8.3%)，最大干密度达到峰值(2.399 g/cm3)，能得到较好密实度的连续级配碎石。最优含水率随级配变化较小，在4.5%～5.5%之间。

图3 7种目标级配试件最佳含水率和最大干密度随级配指数n变化曲线

2 AASHTO T-307试验方法及设备

AASHTO T-307[29]试验规程规定室内回弹模量试验应采用高度为200 mm，直径为100 mm的圆柱体试件。本文所使用材料属于规范中规定的I类材料，需要使用手动振动压实方法进行试件制样。在使用手动振动压实试验进行试件制样时，为了保证试件各处均匀，本文对试件分8层进行压实，并对每层压实高度进行严格控制。图4展示了手动击实制样流程、三轴腔室及外置LVDT位置。

图4 手动击实制样及腔室组装

制样完成后，将试件移入万能试验机DTS-30三轴腔室内进行组装。在三轴腔室顶部传力杆圆盘处固定两个外置LVDT，通过记录传力杆圆盘位移来计算试件在试验过程中产生的回弹变形和永久应变。

AASHTO T-307试验规程为了解决加压腔室安装过程中试样和试样顶盖与底座的接触问题，设置了500～1000次循环的预加载(即序列0)。当预加载阶段试件的轴向永久变形超过原始高度的5%，试验失败，需重新制样。施加的恒定围压σ3为103.4 kPa，施加的循环偏应力σcyclic为93.1 kPa。本文试验预加载采用500次荷载作用次数。

AASHTO T-307试验规程采用加载时长为0.1 s，间歇时长为0.9 s的半正弦脉冲荷载波对试件进行15次加载序列，如表3所示。试件加载序列可分为5组，每组围压相同，轴向应力依次增大。5组围压依次为20.7，34.5，68.9，103.4，137.9 kPa，轴向应力从20.7 kPa增加至275.8 kPa，涵盖了低应力-低围压、低应力-高围压、高应力-低围压、高应力-高围压四种不同的应力组合。每个加载序列设置100个加载循环。

表3 AASHTO T-307粒料类基层/底基层材料室内回弹模量试验加载序列

对于传感器采样频率，AASHTO T-307规定为200 Hz，但是为了能够更加准确的捕捉试验过程中实际施加的脉冲荷载波形并及时修正，保证试验结果的准确性，本文采用500 Hz的传感器采样率。

在计算材料回弹模量时，本文考虑了围压对于传力杆的反作用力Pr，AASHTO T-307对此并未说明。因此，实际施加在试件顶面的最大轴向荷载Pmax应按式(2)计算:

Pmax=Pf-Pr

(2)

式中：Pf为传力杆竖向荷载(kN)。

3 回弹模量影响因素分析

3.1 应力水平对回弹模量的影响

AASHTO T-307试验规程通过5组围压σ3和不同最大轴向应力σmax的组合模拟路面基层材料的应力状态。图5展示了7个目标级配碎石回弹模量Mr平均值随围压σ3和最大轴向应力σmax变化规律。实验结果表明该种材料的回弹模量与最大轴向应力、围压呈现正相关，回弹模量具有明显的应力依赖特性。按照相同的围压将15个加载序列分为5组，虽然每组的最大轴向应力逐渐增加，但增幅低于回弹模量随围压增大的变化幅度。因此说明此种材料的回弹模量受围压的影响明显大于所施加的最大轴向应力。

图5 7组目标级配试件回弹模量与围压和最大轴向应力变化情况

为了更加清晰地分析应力水平对于回弹模量的影响，本文采用体应力θ来综合考虑围压σ3和最大轴向应力σmax，如式(6)所示：

θ=3σ3+σmax

(3)

图6展示了体应力对7组目标级配粒料回弹模量的影响规律。由图6可知，总体上来说较高的体应力呈现出较高的回弹模量值；但回弹模量值并不总是与体应力正相关。如图6绿框所示，级配指数n为0.3，0.35，0.4的凝灰岩碎石试件在同一组围压相同的3次加载序列中，最大轴向应力增大时，回弹模量值反而降低了，但不会持续减小，这与Morgan[30]和Li[31]等人的试验结果一致。然而，n为0.45，0.5，0.55，0.6的凝灰岩碎石试件在该组加载序列中，却又表现出了回弹模量随体应力增大而增大的现象，这与Sweere[32]，Kolisoja[33]以及Wolfe[34]的研究结果一致。说明材料级配对其回弹模量有一定影响，尤其在体应力水平较低的情况下，材料中细集料含量较多时会出现回弹模量随体应力增加而降低的情况。

图6 7组目标级配试件回弹模量随体应力变化

由图6红框所示，当体应力相等时，回弹模量值有显著差异。为此，本文挑选了AASHTO T-307应力加载序列中体应力相等的序列9，11以及序列12，13对最大轴向应力和围压的影响进行进一步的分析。如图7所示围压相同(序列11，12)，轴向应力增大一倍时，7组不同级配的碎石试件回弹模量增大4.0%～14.5%。当轴向应力相等，围压增大33%时(序列11，13)，回弹模量增大10.8～19.6%。而从序列9到序列11，围压增大50%，轴向应力减小100%，7组不同级配的试件回弹模量增长3.1%～13.7%。序列12到序列13，围压增大33%，轴向应力减小100%，7组目标级配碎石试件回弹模量增长0.3%～7.9%。因此可以看出围压应力对于该种粒料回弹模量影响比最大轴向应力更大。

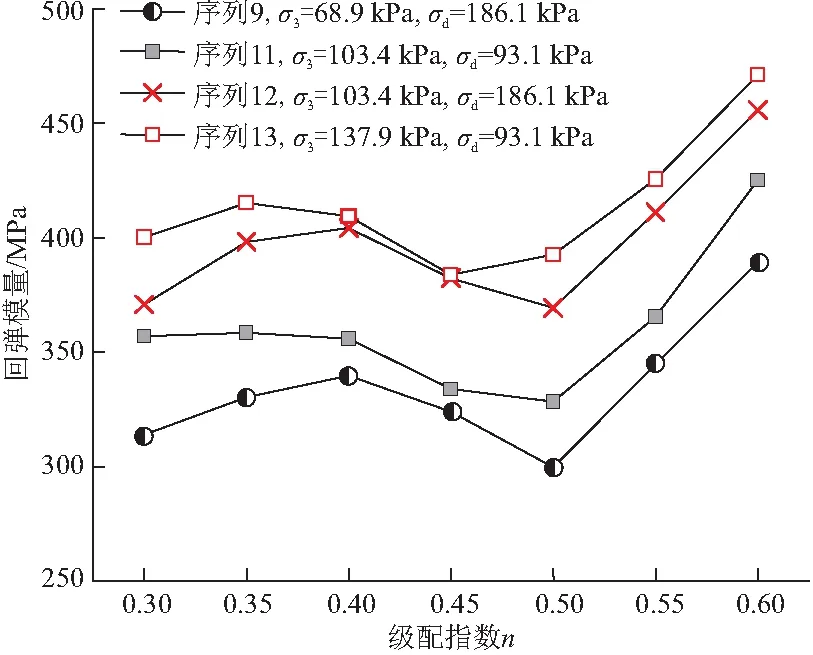
图7 体应力相等的两组序列的回弹模量值对比

3.2 材料级配对回弹模量的影响

图8展示了3次重复试验下级配碎石回弹模量随级配变化情况。3次重复试验情况下该种凝灰岩碎石粒料回弹模量均值随级配的变化趋势相似。单一应力水平下，回弹模量随级配指数n的增大大体上呈现出先增大后减少再增大的非线性趋势，在n=0.5时最小，在n=0.6时最大。由图1展示的级配曲线可知，相较于n=0.6的试件，n=0.5的试件细料含量更多，内部结构更加致密，这就可能导致两个试件含水率在相差不到1%的情况下，水分饱和度有显著差异。粒料的承载机制主要取决于排水条件下骨料之间足够的接触应力和颗粒间摩擦力。额外的水分渗透可能破坏骨料骨架中的粘结，从而导致重复交通荷载下粒料基层的强度和刚度损失。密级配基层/底基层材料表现出较高的干密度，这与低孔隙率导致的渗透性缺陷和排水条件差相吻合。当水分在相对非排水条件下填满所有孔隙时，骨料孔隙中的累计超孔隙水压力，会一定程度上中和颗粒间的接触压力，造成材料模量降低，尤其是在重载交通作用下[35]。

图8 7组目标级配3次重复试验结果

3.3 回弹模量预测模型分析

本文使用7个目标级配凝灰岩碎石材料室内回弹模量试验结果对3种典型回弹模量预测模型(修正k-θ模型、NI模型以及NCHRP 1-28模型)进行拟合回归分析，确定了3种预测模型中的回归系数k1，k2，k3。图9展示了3个预测模型拟合系数R2随级配指数n的变化规律。对于7组目标级配的试件，NCHRP 1-28A模型拟合效果最好，修正k-θ模型次之，NI模型相差较大。NCHRP1-28A和修正k-θ模型的拟合度随试件级配指数n的增大而增加，说明这两种模型更适用于粗集料含量较多的碎石材料的回弹模量预测。

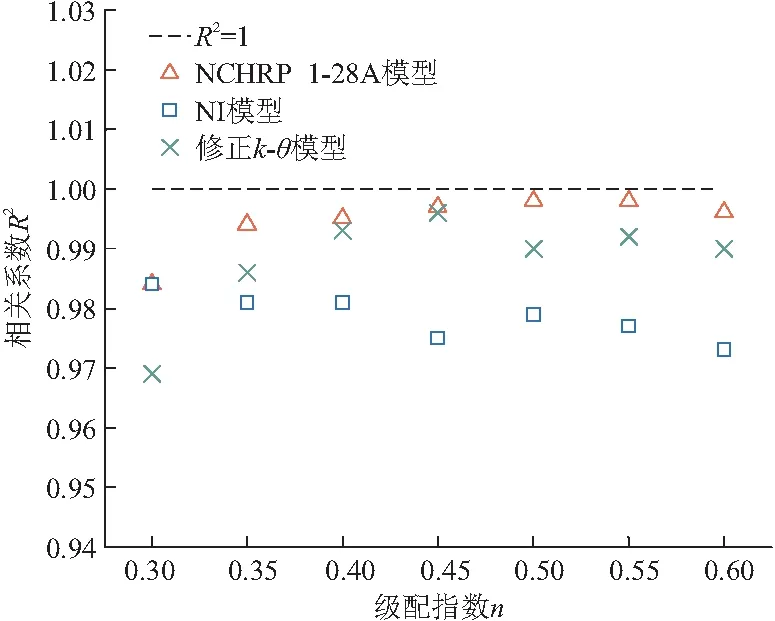
图9 3种预测模型拟合系数随试件级配变化情况

本文将NCHRP 1-28A预测模型回归系数k1，k2，k3与级配指数n进行了相关性分析。图10展示了NCHRP 1-28A预测模型回归系数k1，k2，k3与级配指数n拟合回归图。k1，k2，k3与级配指数n的拟合系数R2分别为0.5236，0.1342以及0.5054，可以看出此凝灰岩碎石材料级配的变化与回弹模量预测模型回归参数相关性较低。