铁路网车流拥堵预判及疏解优化研究
2023-01-18柳佳音何世伟李光晔
柳佳音,何世伟,李光晔
(北京交通大学综合交通运输大数据应用技术交通运输行业重点实验室,北京 100044)
随着我国铁路网的不断建设和发展,运能供给不足问题已得到一定程度的缓解,但由于铁路市场化改革的持续推进,铁路车流时空分布不均衡的特点愈发凸显,故使得全路部分车站、线路仍存在运能紧张的情况.在市场波动下,铁路路网存在阶段性的车流拥堵情况,需要调度部门对运输生产进行统筹考虑,综合安排.目前,我国铁路对车流拥堵的研判与调控完成了一定程度上的信息化改革,但仍主要依赖人工经验.因此研究铁路路网车流拥堵预判及疏解技术,对更好地适应运输市场变化,提升生产管理水平和运输效益,具有重要的理论和实用价值.
就预判方法而言,在道路交通方面,有关学者主要通过模拟实际交通流情况[1-3],从宏观[4-5]、微观[3,6]层面对拥堵形成机理进行研究,预测道路交通流量[7-8],从而预判交通拥堵情况,主要仿真模型包括交 通 流 模 型[1]、智 能 驾 驶 模 型[2]、元 胞 自 动 机 模型[9-10]等.在轨道交通方面,多采用仿真技术[3,6]、指标计算[3,5,11]的方法,基于实际客流数据,计算能力利用率来判别车流拥堵.殷勇等[3]结合熵权法建立换乘站换乘服务水平综合评价模型,通过Anylogic仿真动态模拟乘客在车站的换乘行为,分析车站的瓶颈设备.薛峰等[11]基于铁路列车到发数据,结合城市交通的疏散能力指标计算,对铁路枢纽一日内的车流拥堵情况进行分析.陈卓等[5]基于客流实时数据,计算线路各区间的服务水平综合指标,进行动态网络演变,识别车流拥堵瓶颈.在铁路车流拥堵动态瓶颈研究方面,主要基于车流分配、车流推算的思想展开研究,瞿子涵[12]基于车流分配的思想,构建动态车流组织优化模型获得车流在时空网络上的分配结果,进行车站存车能力比较,从而识别车流拥堵瓶颈节点.王龙等[13]通过车流推算技术,预估目标日期瓶颈区段的动态车流量.综上所述,车流组织优化理论可适用于铁路车流拥堵预判方法的研究.
国内外在车流组织优化方面已有相关研究,主要体现在铁路网车流径路优化问题中,大都采用数学优化模型对问题进行描述.在模型构建方面,主要有点-弧[14-15]、弧-路[16]两种车流径路优化模型,在传统车流径路优化模型中,一般以广义费用最小、综合成本最低[15-16]为优化目标,模型约束条件主要考虑流量守恒约束、路网能力约束、运输时限约束等[14-17].在优化模型求解方面,对于小规模路网数据一 般 采 用CPLEX、Gurobi、Lingo等 求 解 器 求解[14,16-17];对于大规模路网下的车流径路优化问题,主要通过设计启发式算法[18-22]进行求解,常见算法有遗传算法、蚁群算法、邻域搜索算法、粒子群算法等,近年来,列生成、拉格朗日松弛等精确式算法[16,23-24]也被广泛应用于求解大规模路网车流径路优化问题,极大地提高了模型的求解精度.具体而言,毕明凯[16]研究了考虑运输时间和改编作业费用最少的路网车流分配优化问题,并设计了改进的拉格朗日分解算法进行求解.Khaled等[18]提出了异常条件下列车编组和径路协同优化模型,并提出了一种迭代启发式算法解决计算负担.Murali等[19]针对铁路车流径路选择问题建立整数规划模型,并设计遗传算法对模型求解.Samà等[23]针对实时列车运输计划和径路选择优化问题的求解效率提高展开了研究,提出上下界算法提高模型的求解效率.
现有对于车流组织优化的研究缺乏对时间因素的考虑,难以准确描述铁路车流拥堵的产生过程.本文基于给定的铁路网络物理结构,设计离散时空网络描述铁路车流运输过程,从而对车流拥堵预判及疏解问题展开研究.基于车流历史实际走行径路,推算路网车流在规划周期内的流量变化情况,预判车流拥堵的产生;基于车流组织优化理论,构建以总运输里程最小化、运输计划完成率最大化为目标的混合整数规划模型,实现铁路车流拥堵的有效疏解.
1 铁路车流拥堵机理分析
铁路车流拥堵是指加载车流条件下,铁路实时车流量超出运输能力限制,造成车站或区段出现运能紧张的情况,铁路车流拥堵产生过程示意见图1.图1中设定了5个车站,3支车流,车流1与车流2走行径路为A-B-D-E,车流3走行径路为A-B-C-E,随着3支车流的聚集和动态变化,A、B、D站的实时存车数在某个时段超过车站的存车能力,线路A-B、B-D、D-E的车流量在某个时段超过区段的运输能力,形成车流拥堵.若不及时采取措施疏解,会造成车流拥堵现象的进一步传播,严重影响铁路网的运输能力,因此,及时预判铁路网车流拥堵的产生具有重要意义.

图1 车流拥堵产生过程Fig.1 Generation process of railway flow congestion
本文基于车流组织优化,考虑路网运输能力限制,通过数学模型将OD车流合理分配到路网中的车站、区段,从而疏解车流拥堵.
2 车流拥堵预判思路
2.1 基于离散时空网络的问题描述
2.1.1 离散时空网络的构建
给定某一区域的铁路物理网络G=(N,A),N为物理网络中的车站集合,n∈N;A为网络中有向弧段集合,a∈A,oa和da分别为弧段a的起点和终点;定义D为路网中的区段集合,d∈D,对于路网中每个区段d包含两个反向弧段d1∈A及d2∈A,且d1和d2的里程相同,即为路网区段的运输里程.
在给定G的基础上,构建离散时空网络G′=(V,E),如图2所示.以周期Tmax为规划时长,以τ为单位时长对规划时段进行离散化,T为所有时间点的索引集合,T={0,1,2,…,(Tmax-τ)/τ},第t个索引表示时间点t·τ.

图2 离散时空网络示意图Fig.2 Schematic diagram of discrete time-space network
对物理网络中每一个车站节点n进行离散时间拓展,形成时空节点集合V,i、j为时空网络中的节点,V={(ni,ti)|ni∈N,ti∈T};E为 时 空 网 络 中 的有向弧集合,e∈E.假设每个弧段a的运行时间固定且为τa个时间段,为描述列车路网中的运行过程,对于任意a和t,在时空节点i=(oa,t)和时空节点j=(da,t+τa)之间构建运行弧lij,表示该时段弧段a有列车运行,所有的列车运行弧记为El,La为运行径路为弧段a的所有运行弧集合.为描述列车在车站的作业过程,对于任意的n和t,在时空节点i=(n,t)和时空节点j=(n,t+τ)之间构建车站作业弧bij,表示该时段有列车在车站n进行车站作业,所有的车站作业弧记为Eb,Bn为编组站n的所有作业弧集合.E=El∪Eb,mij为弧eij的能力,当弧eij为运行弧lij时,即为列车最大编组数mB,当弧eij为车站作业弧bij时,为车站实时存车能力mC.
2.1.2 车流径路的时空网络描述
F为在规划周期Tmax内存在的车流运输需求集合,(s,t)∈F,qst为车流(s,t)的计划运输流量,μst为车流(s,t)的产生时间,υst为车流(s,t)的运到时间.假设车流能按规定期限运输,根据时空网络中节点车站与时间的对应关系,定义Sst为车流(s,t)产生的时空节点,Est为车流(s,t)消失的时空节点.考虑车流在途中编组站的改编作业时间,要求每支车流运输过程中至少改编λst次,且在改编站停留时间应满足编组作业时间标准τn.假设Tmax=12 h,τ=1 h,规划周期初始时刻为6时,车流运输过程在离散时空网络中的具体表现形式如图3所示,车流①6∶00时在车站1产生,7∶00时从车站1出发,经过区段1-2、2-3,在车站3进行改编作业,再依次经过区段3-4、4-5,18时到达车站5;车流②8∶00时在车站1产生,在车站4进行改编作业,18∶00时到达车站5;车流③6∶00时在车站5产生,在车站4进行改编作业,18∶00时到达车站1.车流在路网中的运输过程即表现为在时空网络中的弧段选择行为.

图3 车流径路示意图Fig.3 Schematic diagram of railway flow paths
2.2 车流拥堵预判方法
受多种实际因素限制,在日常运输组织作业中,货物列车通常按照既定的车流径路运行,并在规定的车站进行改编作业.基于上述思路,将OD车流历史实际径路与时空网络融合,形成实际径路弧段备选集,通过模型求解获得OD车流分配情况.判定实时能力利用率大于95%且持续时间大于3 h的车站、线路形成拥堵,从而根据车流拥堵判定标准,进行铁路车流拥堵预判.铁路车流拥堵预判方法分为4个步骤.
步骤1:基于路网车站线路数据,构建离散时空网络;根据每支OD车流的历史实际径路数据,形成OD车流在离散时空网络中的实际径路备选弧段集合.
步骤2:对于每支OD车流,在车流实际径路备选弧集合中选择一条可行径路,并在相应弧段中进行车流分配,进而获得车流在时空网络中分配方案.
步骤3:统计路网车站线路的实时车流量数据,计算能力利用率.
步骤4:根据车流拥堵判别标准,分析路网车流拥堵形成时刻及区域.
3 车流拥堵疏解模型构建
建立考虑车辆改编和路网运输能力的车流拥堵疏解模型,通过调整车流径路和运输计划,合理分配车流,实现车流拥堵的有效疏解.
3.1 优化目标
车流拥堵疏解模型的优化目标包括总运输里程最小化、运输计划完成率最大化.
1)总运输里程最小化.
考虑运输成本,将车流总运输里程最小为优化目标,表示为

式中:ωij为弧段(i,j)的运输里程;为整数决策变量,表示车流(s,t)在弧(i,j)上分配的车流量.
2)运输计划完成率最大化.
车流拥堵疏解方案应尽可能满足全部车流的装车需求,以运输计划完成率最大化为优化目标,可转化成最小化车流未分配的流量,表现为
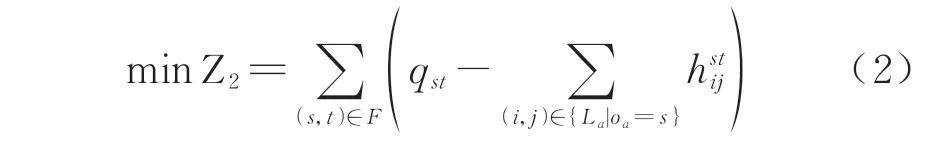
3.2 约束条件
车流拥堵疏解模型的约束条件主要包括节点平衡约束、车流径路调整约束、运输计划调整约束、车流平衡约束、列车最大编组能力约束、车站实时存车能力约束、列车改编作业次数约束、车站作业时间约束.
1)节点平衡约束.
对于任意车流(s,t),由始发节点发出的车流为1,由终到节点流入的车流为1;对于时空网络中非始发、终到的其他节点,输入输出车流相互平衡,从而确保车流运输路径的连续,表示为

2)车流径路调整约束.
对于任意车流(s,t),在同一区段内最多只能走行一次,即在任意弧段a所包含的弧段集合La中,最多只能1条弧段被选择,表示为

对于任意车流(s,t),在同一车站最多只能走行一次.即在以车流始发站s为起、终点的弧段a所包含的弧段集合La中,有且只有1条弧段被选择,在以车流终到站t为起、终点的弧段a所包含的弧段集合La中,有且只有1条弧段被选择,表示为

对于非车流始发、终到站,在以车站n为起、始点的线路a所包含的弧段集合La中,最多只有2条弧段被选择,表示为

计算结果表明,式(5)~式(7)约束车流(s,t)选择一条可行车流径路,且能够避免出现回流.
3)运输计划调整约束.
对于任意车流(s,t),在调整后的车流径路上所分配的流量不能超过车流(s,t)的计划运输流量qst,表示为

4)车流平衡约束.
对于任意车流(s,t),在时空网络中非始发、终到的其他节点,输入输出车流数相互平衡,表示为

5)列车最大编组能力约束.
任意列车运行弧(i,j),分配的车流量不能超过区段列车最大编组能力,表示为

6)车站实时存车能力约束.
任意车站作业弧(i,j),分配的车流量不能超过车站实时存车能力,表示为

7)车流改编作业次数约束.
对于任意车流(s,t),在非始发、终到站的其他车站的改编次数应满足
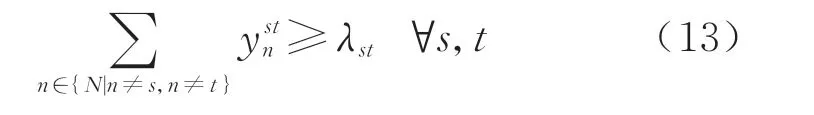

8)车站作业时间约束.
对于任意车流(s,t),在编组站的改编作业时间和始发、终到站的作业时间应满足最低作业时间标准.
车流在改编站的作业时间应满足

考虑车站现存车,车流在始发车站的停留时间应满足

式中:τst为现存车流(s,t)在始发站的车站作业时间;当车流(s,t)为规划周期开始时刻的现存车流时,αst为1,其他情况为0.
车流在终到车站的停留时间应满足

9)决策变量取值约束.
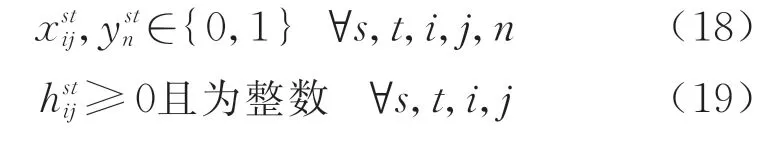
4 算例分析
4.1 基础数据
选取简化后的某铁路局铁路运输网络作为算例,如图4所示,包含19个节点、22个区段.假设所有线路上、下行列车最大编组数相同,旅行速度相同,车站和线路的相关信息见表1、表2.部分车流信息见表3.车流推算周期为24 h,即Tmax=24 h;离散网络单位时长为1 h,即τ=1 h;列车区段运输速度取40 km/h.
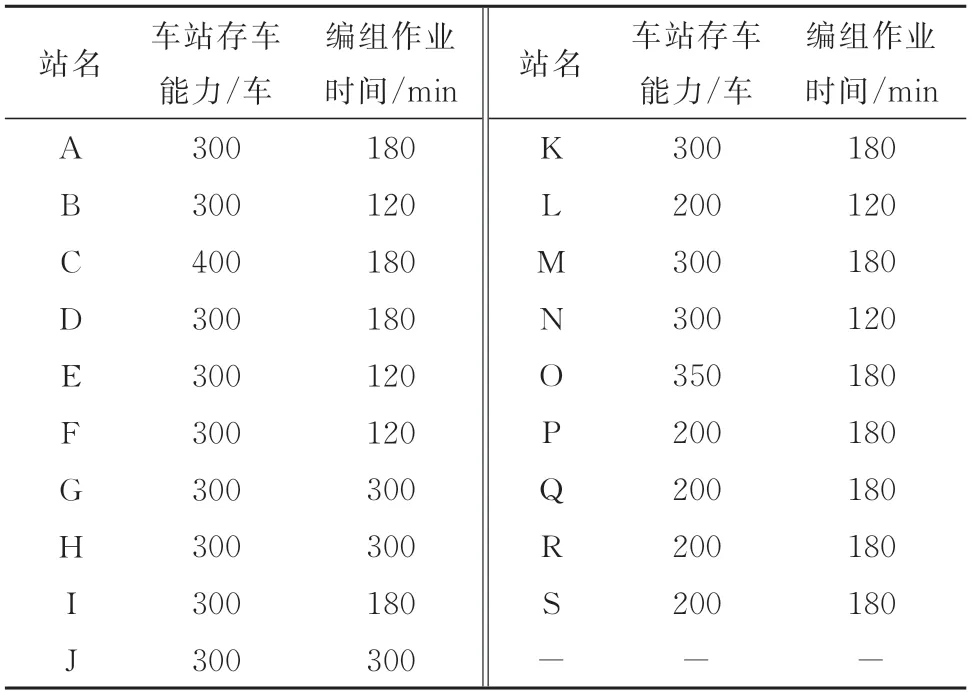
表1 路网车站信息Tab.1 Information of the railway network stations

图4 算例路网示意图Fig.4 Railway network of the numerical experiment

表2 路网区段信息Tab.2 Information of the railway network sections

表3 部分车流信息Tab.3 Information of the railway flow
4.2 模型求解
基于算例路网车站、线路数据,在PyCharm Community Edition 2021.1.1平台上用Python编程构建离散时空网络,生成475个节点、962条列车运行弧、456条车站作业弧;调用GUROBI 9.1.2的API接口,基于分层序列法求解多目标优化模型.
设定目标函数(1)重要程度为1,设定目标函数(2)重要程度为2,首先对目标函数(1)求最优,获得所有最优解的集合R1;进而在解空间R1范围内对目标函数(2)求最优,最终获得模型的最优解及最优值.测试计算机为一台配置Inte(lR)Core(TM)i5-11300H@3.10GHz和16GB内存的笔记本电脑.
4.3 结果分析
设计4个不同规模OD车流数据的案例,从案例1到案例4,车流规模递增,车流拥堵疏解模型的求解结果见表4.根据表4,所有的案例都能在1 h内求得最优解.随着车流规模的增加,受区段列车编组能力、车站实时存车能力约束的影响,在分层序列法下,为满足式(1)取得最优值,会产生部分车流未被分配的情况.

表4 案例求解时间和目标函数值Tab.4 Solving time and objective function values of the cases
求解模型将每支车流加载到时空弧上,获得离散时空网络中的车流分配情况.以1 h为统计周期,统计每小时内路网各车站、线路的实时车流量数据,并计算其实时能力利用率数据.
对案例4车流拥堵预判及疏解结果展开分析,判定实时能力利用率大于95%且持续时间大于3 h的车站、线路产生车流拥堵,统计车流拥堵产生时刻见表5.

表5 车流拥堵产生时刻Tab.5 Time of the railway flow congestion
选取20支车流运行径路求解结果,统计车流拥堵疏解后,OD车流在车流推算周期内的运行径路如表6所示.选取15∶00时路网能力利用率计算结果,绘制车流拥堵疏解前后路网下行方向能力利用分布对比情况如图5所示.由图5可知,当车流按照历史实际走行径路运输时,15∶00时车站L、线路F-G能力利用率超过95%;经调整车流径路和运输计划,15∶00时路网线路能力利用率有效降至80%以下.
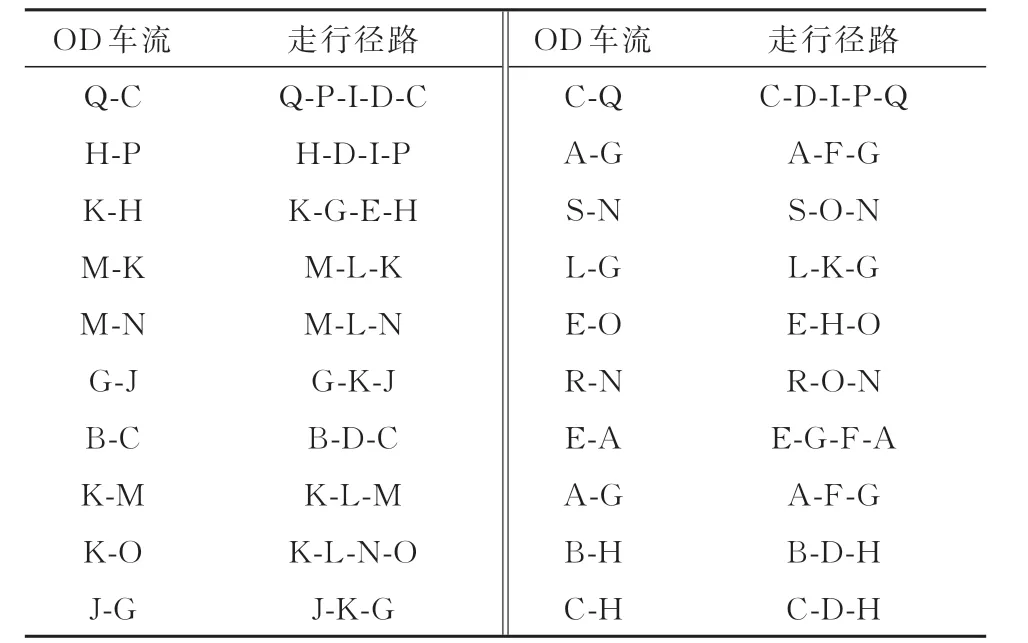
表6 车流走行径路及编组车站Tab.6 Railway flow path and marshalling station

图5 路网能力利用率对比(15∶00)Fig.5 Comparison of railway network capacity utilization(15∶00)
绘制疏解后车站L、车站O的存车能力负荷率变化情况如图6所示,线路A-F、线路L-N的线路能力利用率变化情况如图7所示.由图6可知,在车流推算周期内,车站L、车站O未形成车流拥堵,车站L在8∶00实时存车量达到峰值,存车能力负荷率为100%,持续时间未超过3 h;车站O在次日6∶00时实时存车量达到峰值,存车能力负荷率为92.29%.由图7可知,在车流推算周期内,线路A-F、线路LN的实时存车负荷率均在95%以下,未形成车流拥堵,线路A-F在17∶00时线路能力利用率达到峰值,为94.55%,线路L-N在12∶00时线路能力利用率达到峰值,为69.09%.
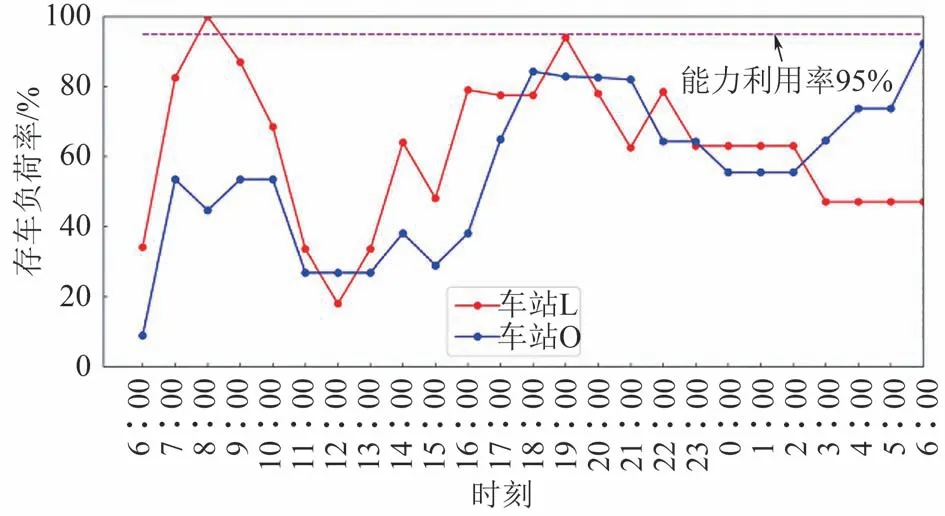
图6 车站存车负荷率变化图Fig.6 Variation diagram of station storage capacity utilization
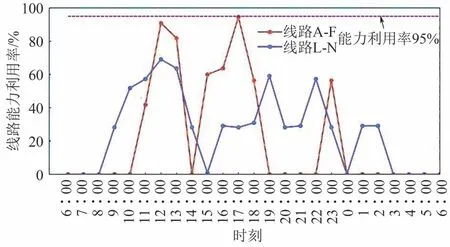
图7 线路能力利用率变化图Fig.7 Variation diagram of line capacity utilization
基于图4算例路网数据,采用传统配流模型[14-15]求解路网车流分配情况,求解时间为0.95 s,对比案例4车流拥堵疏解结果,绘制车站L、车站O、线路A-F、线路L-N平均能力利用对比情况如图8所示.由图8可知,两种模型下的线路平均能力利用情况较为接近,但车站能力利用情况产生一定差距,这是由于案例4中考虑了列车在站停留时间对车站能力占用的影响,造成车站能力利用率偏高,故基于离散时空网络的车流优化模型可准确掌握路网实时拥堵情况,实现车流拥堵的精细化预判与疏解.

图8 经典配流模型与案例4对比Fig.8 Comparison of the results between classic flow assignment model and case 4
以案例4为例分析τ在不同取值时对模型求解效率的影响.根据表7,随着离散时间间隔的逐渐减小,即τ值越小,所构建的离散时空网络中的节点数目和可行弧数目呈倍数增加,货流可选择的可行路径也逐渐递增,模型求解时间越来越长.当τ=0.5 h时,模型在1 h内无法找到可行解,同时,τ值越大意味着列车运行时间及车站作业时间更粗略,求解结果的精细度较差,可见,选取τ=1 h开展研究是较为合理的.
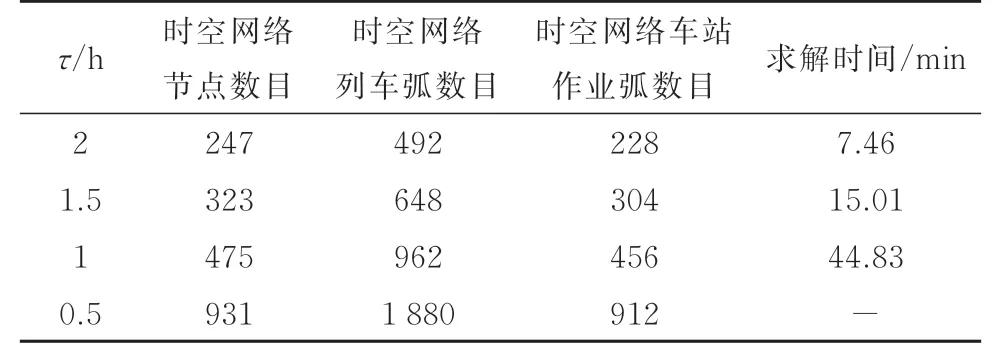
表7 案例4在τ不同取值时的求解结果Tab.7 Results of case 4 with different values ofτ
5 结论
1)基于历史实际车流径路进行路网车流分配,推算规划周期内路网车流变化情况,通过比较实时车流量与路网运能的相对大小,预判路网车流拥堵的产生.
2)研究基于车流组织优化的铁路车流拥堵疏解方法,设计了离散时空网络描述铁路车流径路选择过程,考虑列车改编作业过程、车站存车能力、列车最大编组能力等约束,构建以最小化总运输里程、最大化运输计划完成率为目标的车流拥堵疏解模型.
3)设计实际路网算例,验证了车流拥堵预判及疏解方法的正确性和有效性,通过数学模型求解能实现路网车流拥堵的有效疏解.本文研究对铁路实际运输组织和车流推算工作具有一定的实际参考意义.
