基于经验模态分解与K近邻的轨道交通站点客流预测方法

朱从坤 谢鑫鑫

(苏州科技大学土木工程学院 苏州 215009)

0 引 言

目前城市轨道交通站点客流预测方法可分为单一算法和组合算法.单一算法有时间序列模型、卡尔曼滤波模型、神经网络算法、支持向量机等[1-4].对于组合预测算法则存在更多的尝试可能，包磊[5]建立灰色模型与马尔科夫链的组合模型预测下一时段客流量，但时间粒度为一天，未达到较小粒度客流预测的要求.翁湦元等[6]从时频特性角度分析客流特征，将经验模态分解法的时频分析优势与遗传算法优化的神经网络强拟合能力相结合，探究组合预测算法在高速铁路站点客流预测中的预测效果.黄海超等[7]将变经验模态分解与长短时记忆神经网络组合，对轨道交通客流进行预测，预测效果较好.单一算法的改进和研究较为深入，组合算法的研究则更具灵活性.

经验模态分解(empirical mode decomposition, EMD)能将非平稳、非线性复杂序列分解为较平稳且规律性强的若干本征模函数和残差序列，各子序列能反应原始信号或者序列的内在特征，广泛应用于地球物理信号、机电系统故障、语音信号以及金融类和客流量等较为宏观的非线性时间序列的处理.罗述群等[8]利用EMD对景区人流量时间序列进行分解、预测，预测精度较好.赵阳阳等[9]将经验模态分解与神经网络结合预测短时地铁客流，模型有效降低样本噪声对客流预测的干扰，提高了预测精度和时效性.陆利军[10]利用EMD对游客量数据与网络搜索数据进行降噪处理，将ARIMA模型与BP神经网络进行组合预测客流量，预测效果较好.

K近邻(k-nearest neighbor，KNN)作为非参数回归方法的一种，不对数据做任何严格处理，仅依赖现有数据序列决定预测值的输出，无需任何先验知识且参数少.郭晗等[11]在轨道交通客流预测中研究了K近邻算法中状态向量的选择，结果表明以预测时段前m个时段的历史数据作为状态向量具有较好的预测效果，而相邻站点历史客流数据由于其相对独立，不宜作为状态向量.刘美琪等[12]对比不同预测算法在轨道交通进站客流预测上的效果，发现K近邻的总体预测精度最高，贝叶斯组合预测算法次之，基于偏差修正系数的卡尔曼滤波模型在早晚高峰时的适用性较差.

综上所述，经验模态分解能将非平稳、非线性序列平稳化分解，K近邻算法无复杂参数，且有较强的数据挖掘能力，为此本文拟探讨经验模态分解与K近邻的组合算法(EMD-KNN)在轨道交通站点进站客流时间序列预测中的应用效果.

1 研究方法

1.1 经验模态分解(EMD)方法

经验模态分解步骤为

步骤1找出序列x(t)所有的极大值和极小值点.

步骤2用三次样条曲线拟合出上下极值点的包络线emax(t)和emin(t)，并求上下包络线均值m1(t)，在x(t)中减去m1(t)，得到新的序列h1(t).

h1(t)=x(t)-m1(t)

(1)

若h1(t)不满足本征模函数的确认要求，则将h1(t)作为新的原始序列x1(t)，重复步骤1～2，直至得到的某个hk(t)满足本征模函数预设要求.本征模函数需满足两个条件：①该函数hk(t)的过零点数和极值点数最多差1；②局部极大值点和极小值点形成的两条包络线的平均值趋近于零.

步骤3令得到的第一个满足本征模函数要求的hk(t)记为IMF1，将IMF1从原始序列x(t)扣除得到序列r1(t)，作为新的原始序列，重复步骤1～2，直至得到的某个rn(t)为单调函数或简单趋势函数，将其作为残差序列.

原始序列被分解为若干个IMF分量和残差序列R，即

(2)

1.2 K近邻非参数回归(KNN)

1.2.1KNN原理

考虑到轨道交通站点预测时段客流量与相邻时段客流量具有相关性，可选取预测时段前q个时段的客流量作为状态向量(即认为该q个时段的客流量与预测时段客流量密切相关)，利用状态向量在历史数据中进行匹配，得到与预测时段客流量最为接近的K组历史数据，对这K组预测时段历史数据进行处理得到预测结果.其中，K值可由样本测试法确定；q值由日时间序列q阶自相关系数确定，通过计算众多历史序列不同阶自相关系数ρx,q，统计各阶ρx,q≥0.3的序列个数占总历史序列数的占比情况，取占比较大的阶数为q.序列q阶自相关系数为

(3)

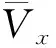
1.2.2K近邻预测方法

传统K近邻预测算法是将K个近邻的客流数据算术平均值作为预测值，然而匹配到的近邻对象与预测对象距离不尽相同，其对预测对象值的贡献也是不同的，因此有必要基于近邻对象与预测对象距离越小权重越大的原则，对K个近邻对象设置权重，通过加权平均得到预测值.

若客流量预测日为O，预测时段为t，由状态向量匹配到的K个近邻对象的日期分别为D1,D2,…,Dk，则预测算法为

(4)

(5)

式中：PO,t为预测日O在时段t的小时进站客流量预测值；αk为近邻Dk的预测权重值，各权重值之和为1；dk为预测日O的状态向量与近邻日Dk的状态向量之间的欧式距离；Hk,t为近邻日Dk在时段t的历史客流量值.

1.3 EMD-KNN组合算法

EMD-KNN组合算法流程见图1.

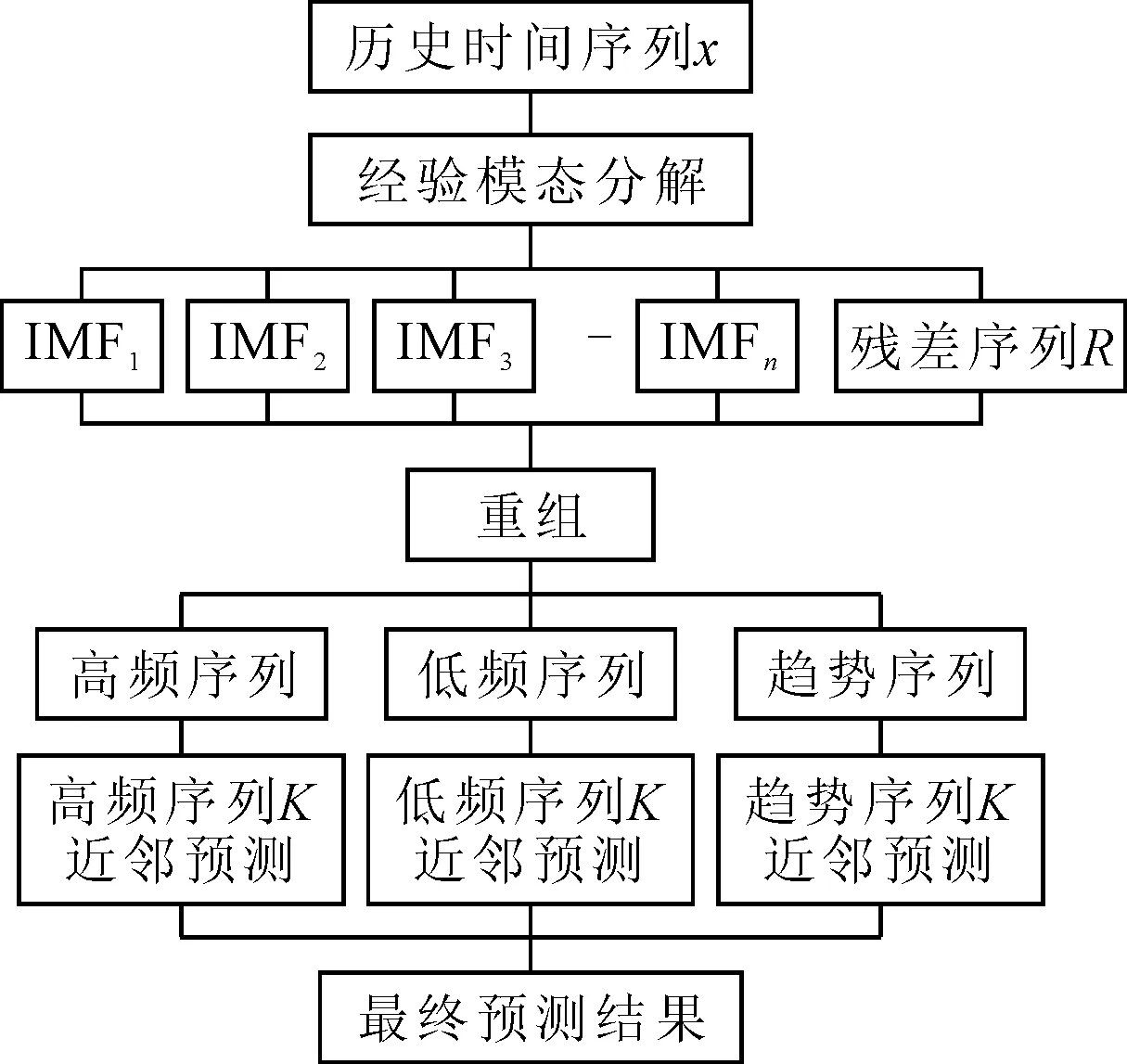
图1 EMD-KNN组合算法流程图

2 实例站点客流特征分析

2.1 站点客流时序变化特征

选取苏州轨道交通1号线换乘站点广济南路站进站客流为分析实例，客流历史数据统计自2020年1月1日—6月22日，时间粒度为1 h，7时的客流量定义为06:00—07:00的小时客流量，以此类推，每日共17个时段.图2为小时进站客流量时序图.

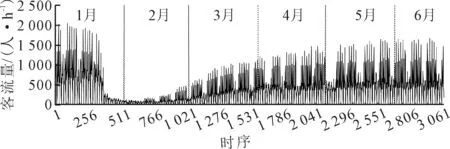
图2 2020年1月1日—6月22日广济南路站小时进站客流时序图

由图2可知：客流量在1月上旬较为正常，但受到新冠肺炎疫情相关交通管制措施的影响，1月中下旬出现断崖式减少，低位客流量持续一个多月；受复工复产影响，2月中下旬至5月，客流量缓慢爬升；6月客流量逐渐恢复，但较疫情前依然略低.宏观上，客流量时序呈非线性变化趋势；中观层面，以周为单位，客流量呈现明显的周期性，各工作日客流量普遍高于非工作日.

疫情前后日小时变化曲线有明显差异，见图3.疫情前，1月3日为工作日，客流时间序列呈现明显早晚高峰特征；1月11日非工作日，无明显早晚高峰.2月为疫情严防期，其中2月21日工作日出现不明显的早晚高峰，2月22日非工作日无早晚高峰.由于疫情得到有效控制，5月5日非工作日客流量较2月有较大提高，且随着复工复产，5月8日工作日客流量小时变化特征接近疫情前.总体上，站点进站客流量小时序列呈非线性、非平稳，同时具有周期性变化的特征.

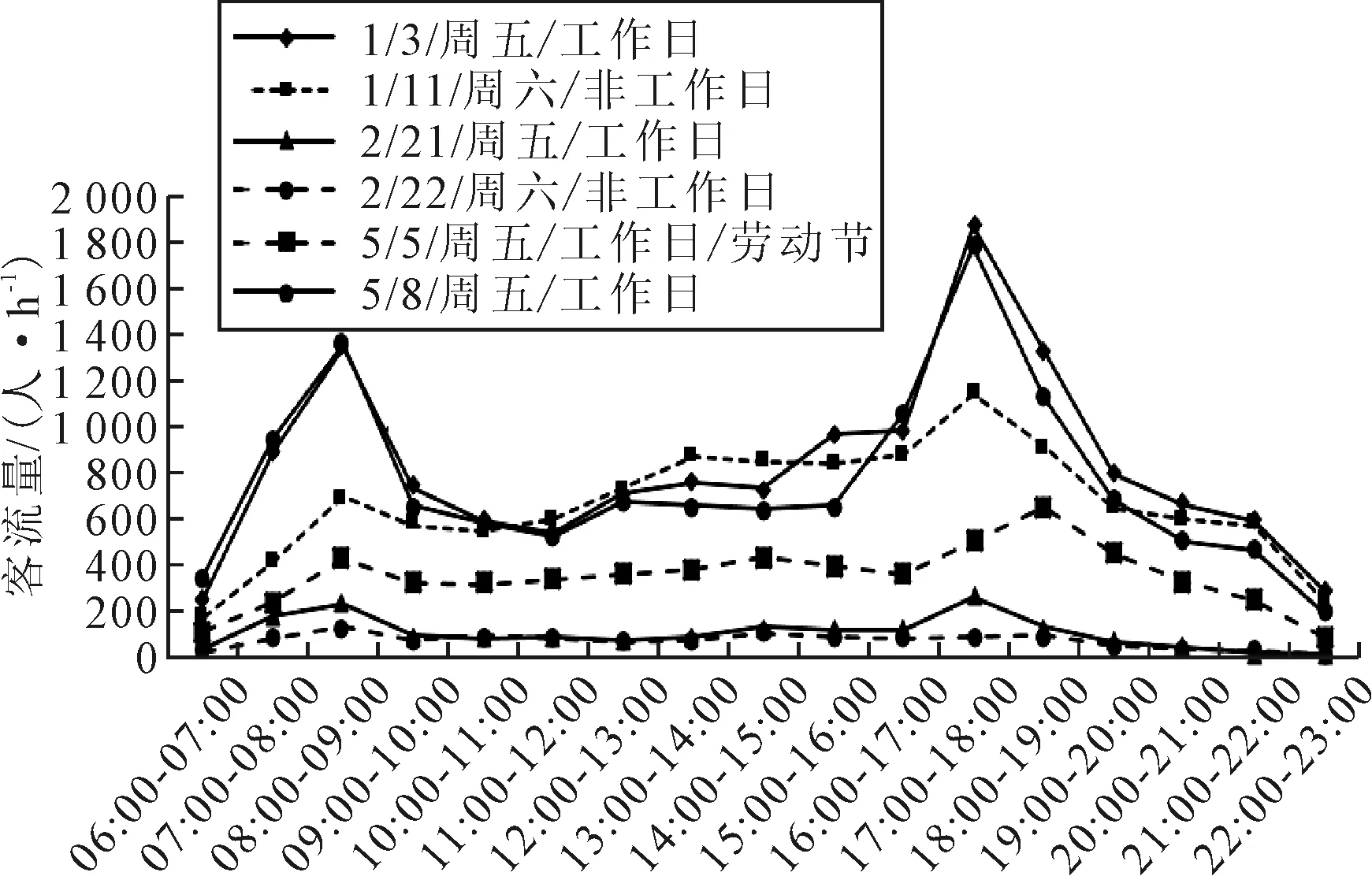
图3 广济南路站疫情前后小时客流变化对比

2.2 时间序列结构断点识别

利用计量经济统计软件Eviews，对2020年1月1日—6月22日的站点小时进站客流序列进行BP结构性多断点检验，检验结果见表1.

由表1可知：在0.05显著性水平下，断点检验“0vs1”、“1vs2”、“2vs3”的F值大于临界值，拒绝了1、2、3三个断点差异显著为0的假设；断点检验“3vs4”的F值小于临界值，无法拒绝原假设.由此判断3个结构断点位置大致为1月23日、3月11日和5月2日，各断点时间基本与地方政府采取疫情交通管制措施和复工复产时间相一致.三个结构断点将时间序列分为T1、T2、T3和T4四个子序列段，见图4.

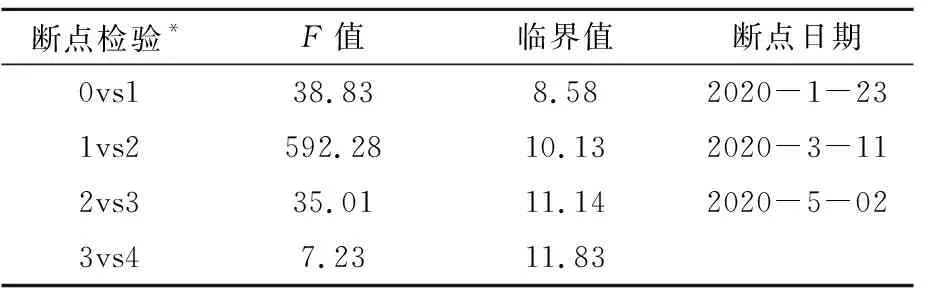
表1 BP结构断点检测结果

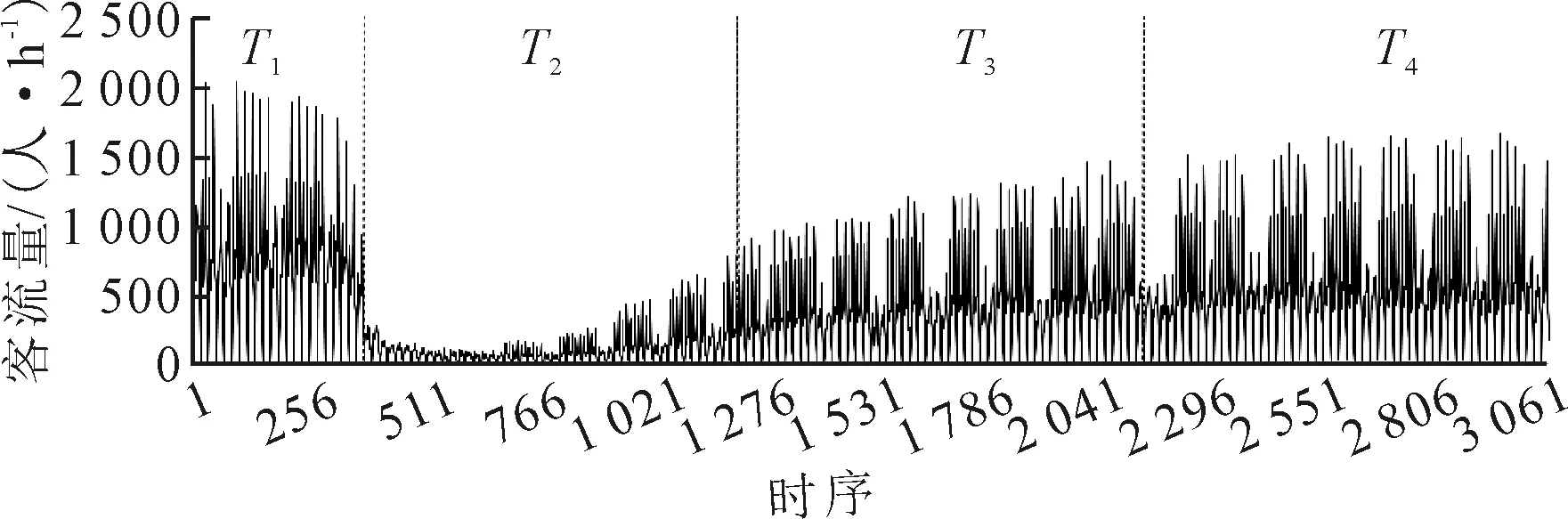
图4 2020年1月1日—6月22日客流时间序列结构断点分段图

3 基于EMD-KNN的站点客流预测

以2020年6月19 —22日4 d的小时进站客流量为预测对象，选取客流变化趋势与预测日最为接近的T4序列作为历史数据序列.

3.1 时间序列EMD分解

基于Matlab平台编写经验模态分解运算程序，对历史数据序列进行经验模态分解，得到8个本征模函数IMF1-IMF8，以及一个残差序列R，见图5.

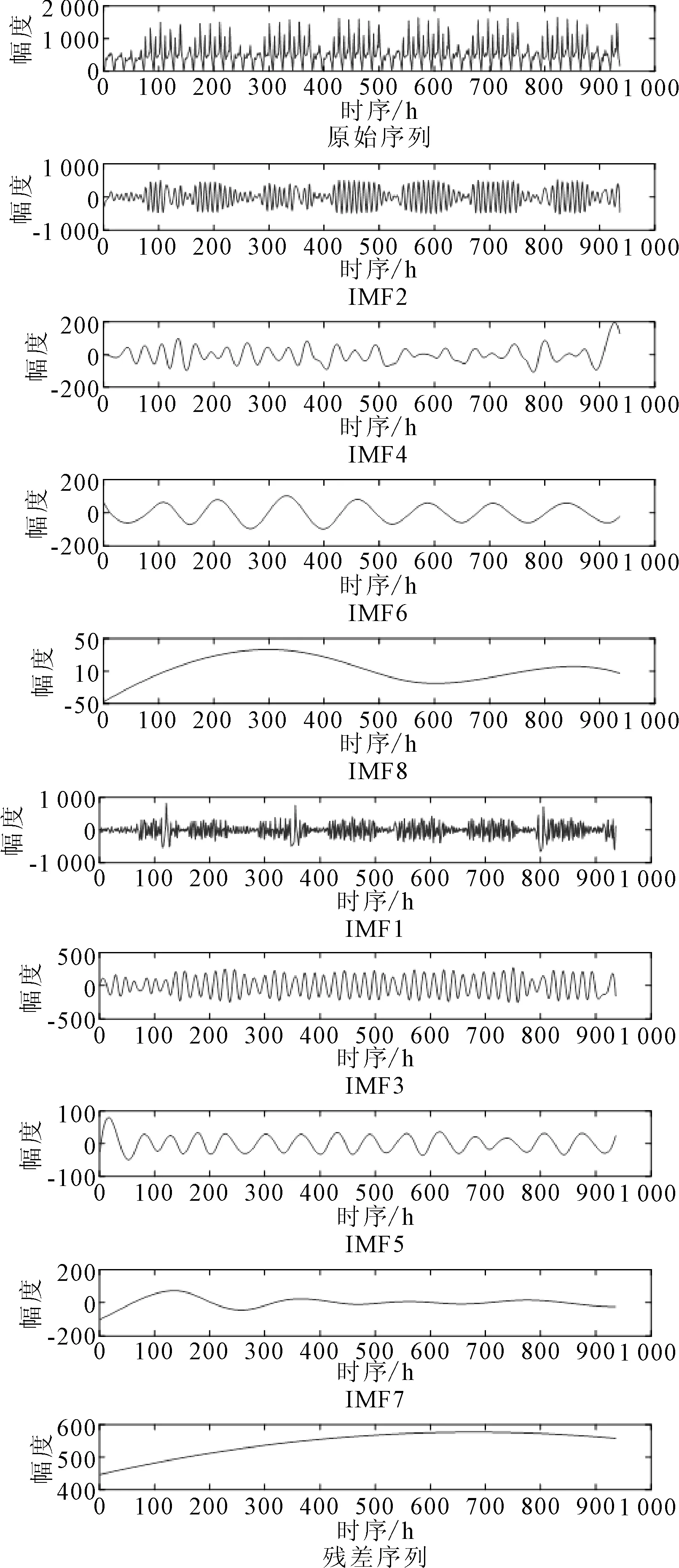
图5 2020年5月2日—6月18日客流时序经验模态分解结果

由图5可知：本征模函数IMF1-IMF8波动频率依次降低，波动周期逐渐增大，最终的残差序列波动频率最低，是原始序列的总体发展趋势.

3.2 本征模函数IMF分组

计算各IMF和残差序列与原始序列的相关性系数、方差占比、样本熵、周期等统计指标，结果见表2.

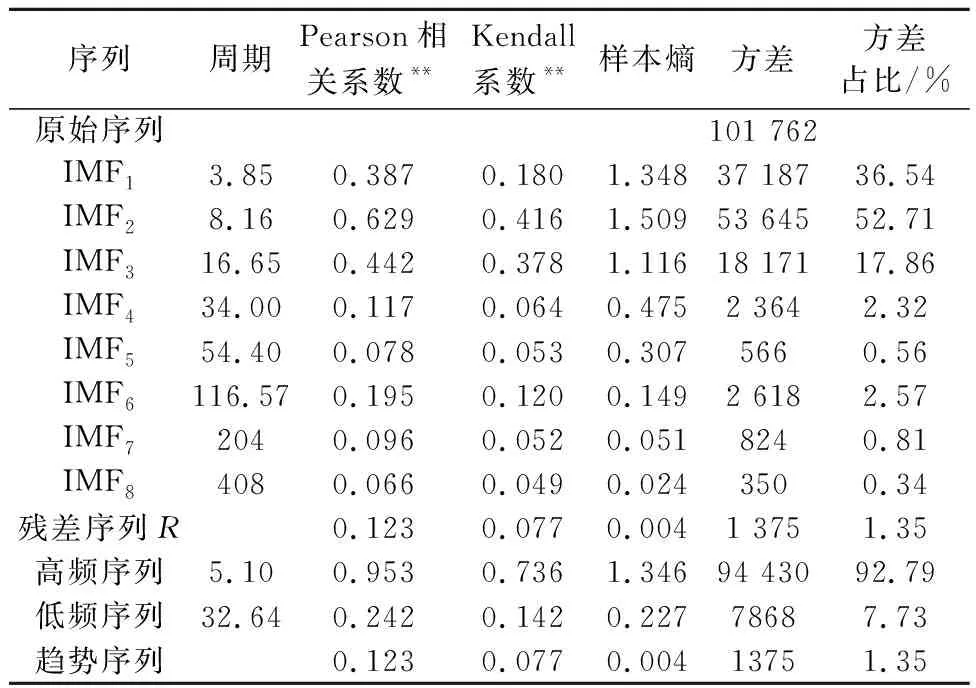
表2 各分量统计指标

由表2可知：IMF1～IMF8的平均周期逐渐增大，IMF3平均周期为16.65，表达每日统计的17个时段的周期尺度， IMF2为半日的周期尺度，IMF6为一周的周期尺度.IMF分量的周期尺度能明显反应原始序列部分尺度特征.

Pearson相关系数和Kendall系数衡量两序列之间的相关性.IMF1～IMF3与原始序列的Pearson相关系数及Kendall系数均显著大于其它分量，IMF1～IIMF3包含了原始序列的较多特征.样本熵表征序列的复杂程度，IMF1～IIMF3的样本熵远大于后续IMF分量，表明IMF1～IIMF3分量序列本身也具有较高复杂性.

IMF1～IIMF3的方差占比远大于后续分量，表明这三个分量反应了大部分原始序列波动情况；残差序列方差占比仅为1.35%，表明原始序列总体走向趋势较稳定.

由于经验模态分解本身会存在分解误差，为避免分解序列过多导致的误差累积，综合考虑IMF1～IIMF3组合为高频序列，IMF4～IIMF8组合成低频序列，残差序列单独为趋势序列.组合后的高、低频序列和趋势序列见图6，相关统计指标见表2.由表2可知：高、低频序列各相关系数明显增大，表明原始序列大部分的波动特征可以被高、低频序列表达.

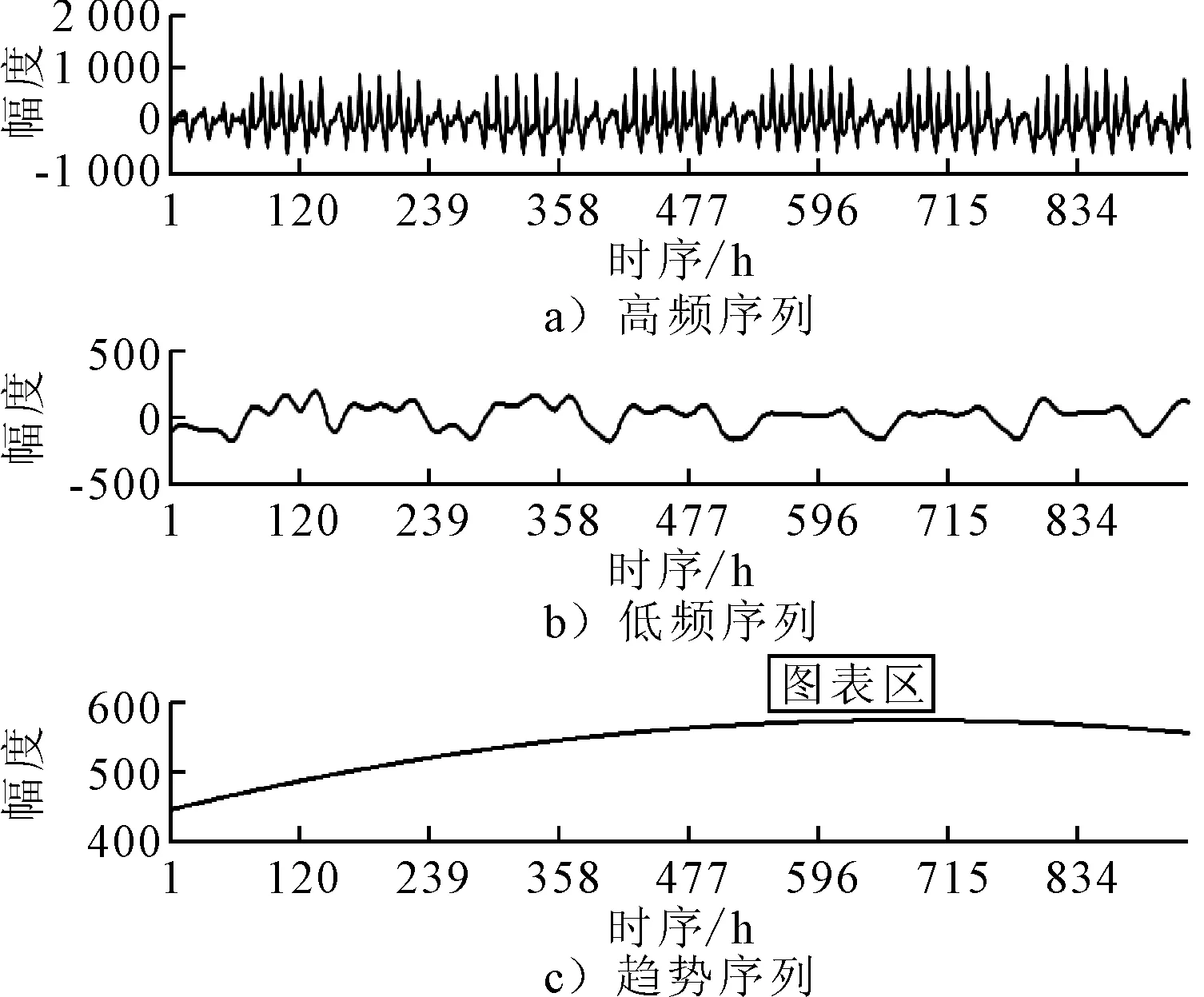
图6 高、低频及趋势序列分组结果

3.3 KNN参数确定

统计2020年5月2日—6月18日期间，站点每日时间序列1～4阶自相关系数ρ≥0.3的日序列占比情况，结果发现日时间序列滞后2个时段的统计占比为94.83%，滞后3个时段的统计占比仅为1.72%，可认为预测时段前2个时段的进站客流量与预测时段具有良好的相关性，以预测时段前的2个时段客流量作为状态向量.

以2020年6月15—16日小时进站客流量作为确定K值的测试样本，以2020年5月2日—6月14日的客流量作为历史数据序列，取预测时段前两个时段客流量作为状态向量，状态向量的匹配距离采用欧氏距离，计算不同K值下测试样本的平均绝对百分比误差，结果见图7.

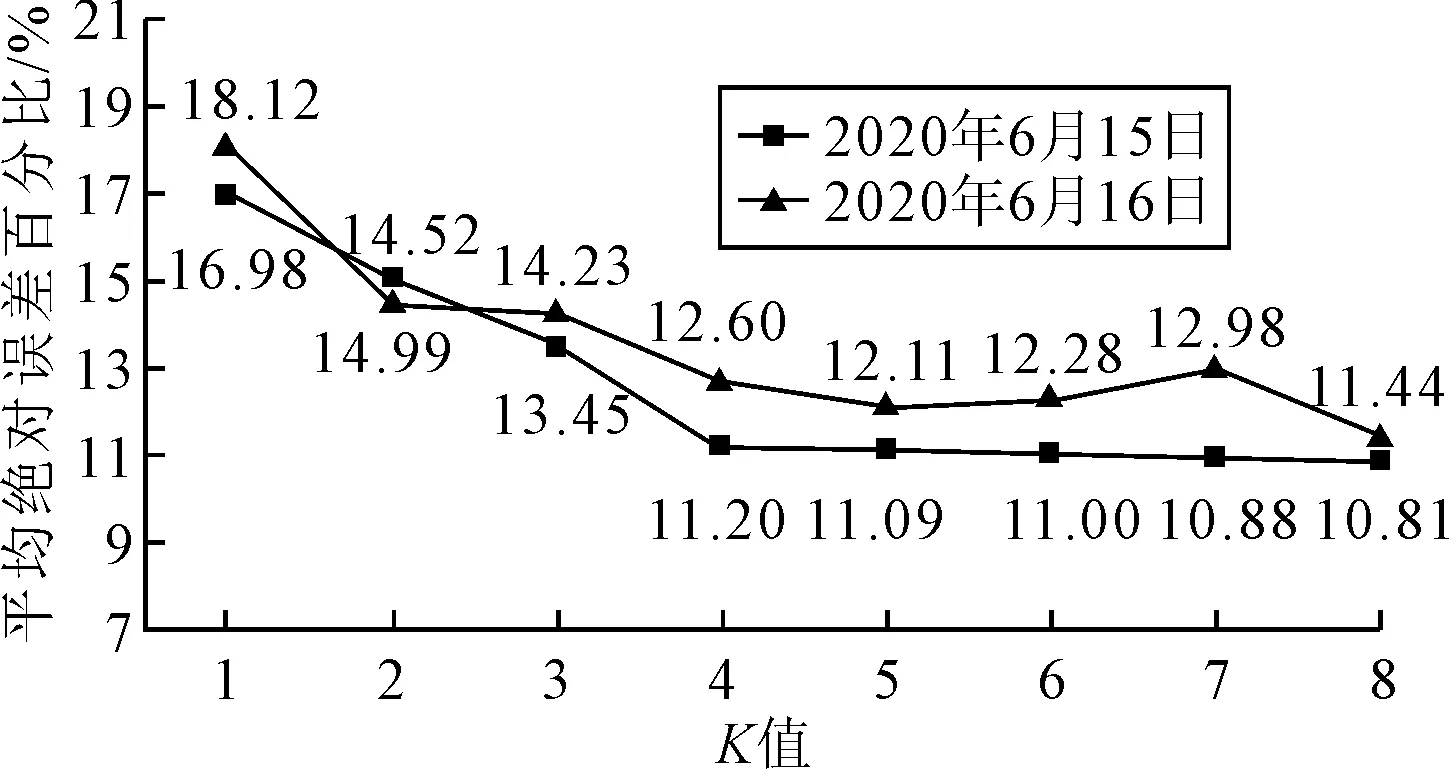
图7 不同K值下测试样本误差统计

由图7可知：对于6月15日测试样本，K值取1～4时，平均绝对百分比误差从16.98%降至11.20%，K值取4～8时，平均绝对百分比误差仅降低0.39%；对于6月16日测试样本，K值取4～8时，平均绝对百分比误差仅降低0.84%.说明较大的K值对于提高预测精度并无明显作用，因此取K值为4，既能保证较好的预测精度，又可提高计算效率.

3.4 客流预测结果

分别采用EMD-KNN组合算法、单一KNN算法和ARIMA模型对6月19—22日的广济南路站小时进站客流进行预测，其中19日、22日为工作日，20、21日为非工作日，预测结果见图8.

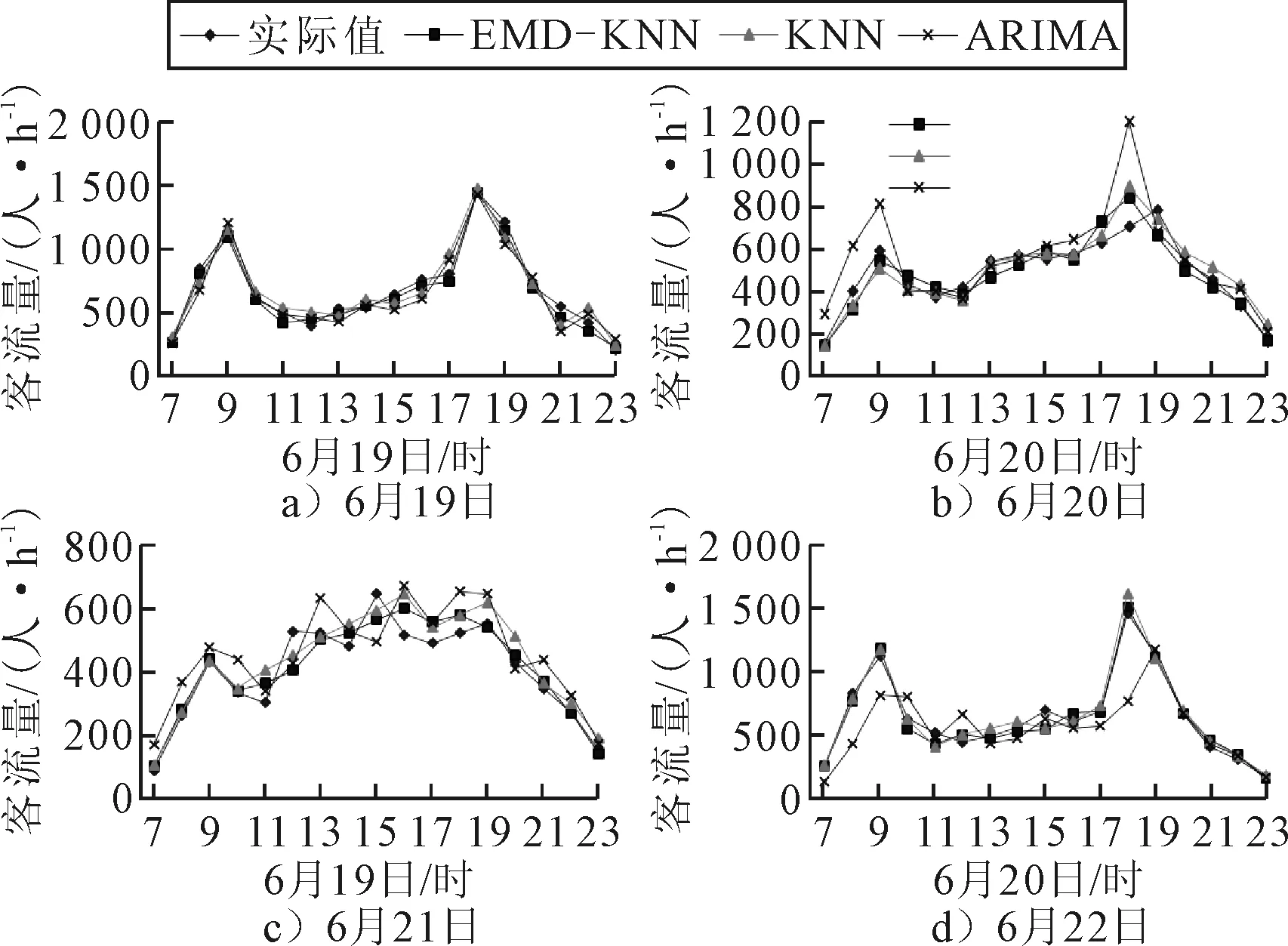
图8 EMD-KNN/KNN/ARIMA预测结果

由图8可知：EMD-KNN组合算法与单一KNN算法在预测结果的变化趋势上与真实值高度一致，而ARIMA模型仅在19日预测趋势与实际值相似，其余3 d的预测趋势相差甚远.20日为非工作日，ARIMA预测结果却出现早晚高峰，21和22日预测结果与实际值存在较大偏差，这是因为ARIMA模型周期性参数设定较为固定，导致难以区分工作日与非工作日的变化规律，尤其当出现节假日调休时，预测误差会更大.

3.5 预测精度对比分析

利用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)三个指标反映预测精度，各指标汇总见表3.

表3 三种算法预测精度汇总表

由表3可知：EMD-KNN、KNN和ARIMA在四天预测日的平均绝对百分比误差均值分别为8.74%、12.03%、20.74%，与KNN算法、ARIMA模型相比，EMD-KNN组合算法精度更高，更加适合不区分工作日和非工作日的小时客流时间序列预测，全日预测趋势与真实值趋势高度匹配.

4 结 论

1) EMD-KNN组合算法与KNN算法均能有效捕捉全日客流变化趋势，在预测时间粒度为1h以及不区分工作日和非工作日情况下，EMD-KNN组合算法预测精度优于KNN算法，精度能保持在90%左右，后续可进一步讨论不同时间粒度下的预测效果.

2) 由于研究站点本身为通勤类换乘站点，其工作日客流特征较非工作日更明显，因此存在工作日预测效果相对优于非工作日，后续可进一步研究EMD-KNN组合算法在不同类型站点的适用性.

3) 本时间序列预测中，ARIMA模型预测精度不高，这是由于该模型周期性参数设定较为固定，较难区分工作日与非工作日的变化规律，以及调休等因素带来的影响.