山地城市立交基本段通行能力研究

龚华凤 杨 进 周约珥

(林同棪国际工程咨询(中国)有限公司1) 重庆 401121) (重庆市山地城市可持续交通工程技术研究中心2) 重庆 401121)

0 引 言

道路通行能力是道路规划设计与运营管理过程中的重要参数之一.自上个世纪30年代起，国外学者便开始了对通行能力的研究，并积累了大量成果.美国的Highway Capacity Manual(HCM)[1]最早提供了具有本地特征属性的通行能力建议值及其影响因素的量化指标，成为了其他国家制定通行能力标准的范本.为了制定符合本国特征的通行能力标准，德国[2]、西班牙[3]等国学者在借鉴其方法的同时，均进行了本地化与再创新.我国对通行能力的研究则起步较晚，始于上世纪80年代初[4].然而，国内本地化研究的基础数据多采集于地形平坦的平原城市，关于山地城市的研究较少，尤其在山地城市道路纵坡大、路幅狭窄、异型立交多等特定条件下，其通行能力与平原城市相比有明显差异.考虑到互通立交一般由基本段、合流段、分流段，以及交织段组成，各部分的交通流特性、通行能力评价方法均存在较大的差异，其中基本段又是立交各部分通行能力研究工作的基础，因而本研究首先对基本段开展了相关研究工作.

传统的道路通行能力计算模型主要包括速度-密度关系模型、车头时距模型等，这些模型侧重于描述交通流特性与通行能力之间的关系，无法反映道路几何线型、交通组成等因素对通行能力的影响.针对平纵几何线型，刘江等[5]通过分析山区公路的曲线半径和纵坡对通行能力的影响，发现当半径大于400 m或道路纵坡小于3%时，道路平纵对通行能力几乎没影响.针对车道宽度因素，Khanorkar等[6]研究发现车辆类型决定了车道宽度对通行能力影响的强弱.而Cao等[7]认为车道的有效宽度才是影响通行能力的关键，如车辆变道、路边停车等均会降低车道有效宽度.针对影响通行能力的路侧因素，Munawar[8]提出了路侧阻力的概念，并以此建立了考虑多因素的通行能力预测模型，研究结果认为路侧停车是影响交通流运行速度、通行能力的主要因素.但该模型的应用范围有限，尤其当路侧阻力较大时，模型的结果误差偏大.孟祥海等[9]针对施工区路段的通行能力开展了实证工作，并结合换道率曲线、速度分布曲线等提出了相关优化建议.

上述学者基于不同的侧重点，讨论了道路几何线型、车道宽度、路侧条件等因素对通行能力的影响，建立了对应的量化关系.然而，多数研究考虑的影响因素较单一，相应的研究成果难以直接应用于道路环境更加复杂的山地城市.因此，本研究采集了重庆市各区不同立交基本段的交通流与道路几何线型等数据，筛选并确定了多个通行能力影响因素，建立了基于Panel Data的主线基本段通行能力预测模型(后文简称主线模型)、匝道基本段通行能力预测模型(后文简称匝道模型)，讨论了本研究模型计算结果与国内外通行能力标准的差异，并给出了不同类型、不同速度下对应的山地城市立交基本段通行能力建议值.

1 数据采集与处理

通过固定检测器与录像的方式，采集了重庆7个主城内14座立交基本段的交通流数据，共计99.485万条.利用车辆行驶过程中产生的GPS定位数据，通过Civil 3D软件平台拟合得到道路几何线型数据.其他数据均通过实际调查获得，如设计速度、限速、大车比例(城市中的大车以公交为主)等.

针对由速度、流量、密度组成的多元交通流数据，基于马氏距离的KNN算法[10]，对缺失数据进行了挖掘补全.基于数据挖掘的结果与GB/T4883—2008《数据的统计处理和解释正态样本离群值的判断和处理》的建议，运用马氏距离对特定置信度下的离群值进行了清洗.其中，小于1%置信度筛选得到的离群值为统计离群值，予以删除；介于1%与5%置信度筛选得到的离群值为歧离值，采用时间序列方法进行清洗.

经过数据挖掘与数据清洗，共剔除了3.330万条异常数据，占总采集数据的3.350%，得到的有效数据共计96.155万条.

2 立交基本段通行能力预测模型

2.1 建模方法

采用Panel Data进行建模，该类模型有助于降低横截面数据的异方差性和时间序列中的多重线性干扰，可较好地应用于多因素分析，其基本表达式为

y(i,t)=β0+β1x(i,t)+…+βjx(i,t)+μ(i,t)

(1)

式中：y为模型因变量；i为样本编号；t为时间序列；β0为个体效应；β1～βj为模型截距；μ为剩余变量；x为模型自变量.

2.2 通行能力影响因素

针对道路平面线型，考虑圆曲线的半径Rh与长度Lh、平曲线的转角a与长度Lshs等对通行能力的影响[11].

针对道路纵向线型，目前研究得出的结论各异，尚未形成统一的认识.Morrall等[12]的研究发现交通流中的旅游车(常为大型车辆)决定了纵坡对通行能力的影响，Zegeer等[13]则基于敏感度分析认为纵坡是通行能力的中低影响因素，文献[5]则认为只有当纵坡大于3%时才会影响道路通行能力.考虑到山地城市特殊的地形地势，本研究考虑了多种道路纵向线型因素，将竖曲线的半径Rv与长度Lv、竖曲线前坡ii与后坡io，以及前后坡差iiod等因素统一加入模型分析.

针对道路的横向线型，文献[13]已经分别证明了车道宽度和路肩宽度等对通行能力的影响较弱，为非主要影响因素，故在本研究中不再考虑.针对其它因素，本研究考虑了普遍认可的通行能力影响因素，如道路的限速vp、设计速度vd、大车比例phv、运行速度vo等.

对不同因素与通行能力之间的相关性进行了Pearson检验，并以此作为筛选最优模型的主要依据之一，检验结果见表1.

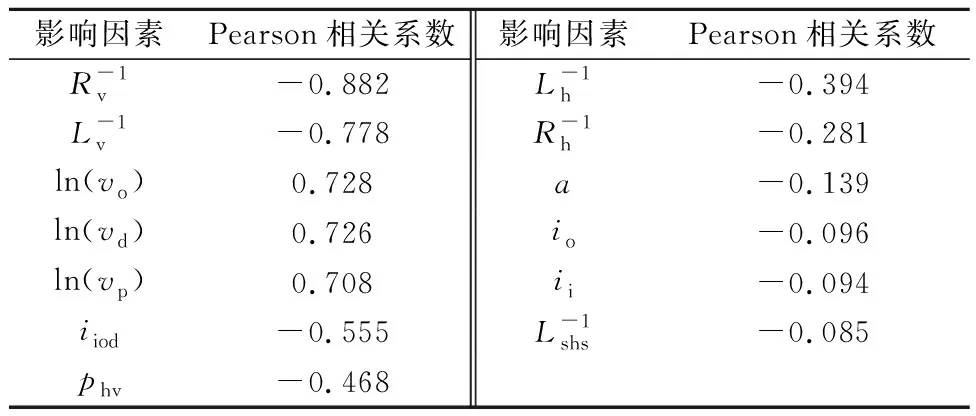
表1 Pearson检验结果

2.3 建模概述

针对特征差异较大的立交主线与匝道分别建模，数据集均按7:3随机分为建模组和验证组.随后通过不同因素的组合，基于STATA软件平台实现Panel Data建模(5%置信度).最终模型则通过显著性检验P值、R2等建模指标与结合前述的Pearson检验结果确定.

2.4 主线模型

基于主线建模组数据得到的主线模型，见式(2)和表 2.

(2)

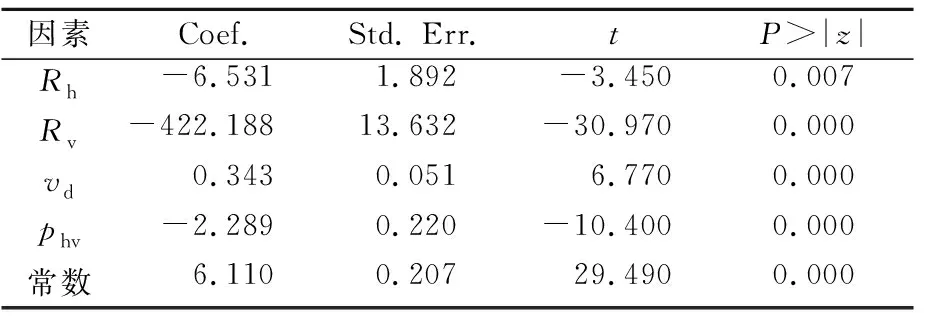
表2 主线模型建模结果

由表2可知：模型的整体拟合效果良好(R2≈0.989)，各主要因素的相关性与Pearson检验一致.同时，为保证主线建模结果的合理性，本研究依次对模型的多重共线性、残差等进行了检验.检验结果显示，主线模型的方差膨胀系数为1.940(<10)，表明主线模型各参数之间不存在因参数之间的高度相关导致模型结果出现偏差的问题；主线模型残差的K-S检验P值为0.484(>0.05)，表明主线模型的残差符合正态分布.

基于建模结果与验证组数据，研究通过预测误差对模型的泛化性进行了验证，见图1.由图1可知：其误差在[-7.556%,6.847%]区间内.此外，相应的相对误差平均值(2.740%)、中位数(2.166%),以及标准差(2.240%)均处于较低水平.上述指标均表明，主线模型误差相对较低，泛化性良好.

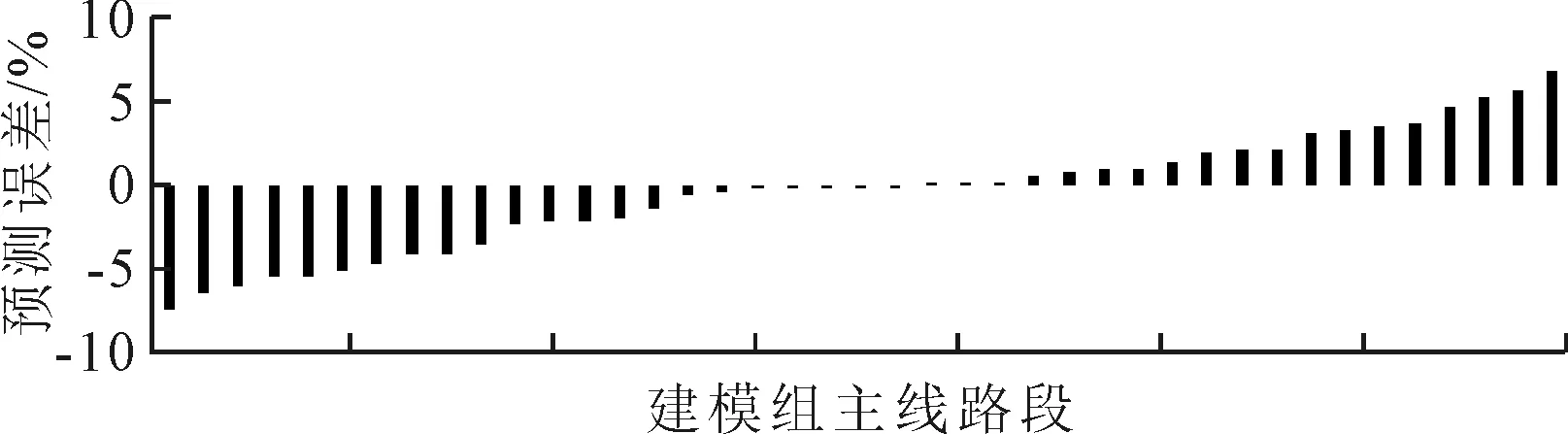
图1 主线模型预测误差

2.5 匝道模型

基于匝道建模组数据得到的匝道模型，见式(3)和表3.

In(C)=7.417-0.067a-

(3)

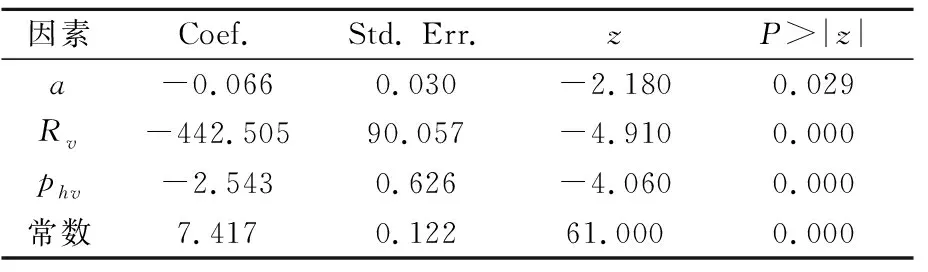
表3 匝道模型建模结果

建模结果表明:模型的整体拟合效果良好(R2≈0.957)，各参数的相关性与Pearson检验一致.与主线模型相比，匝道模型不包含设计速度因素.导致该结果的原因主要表现在两方面：①重庆市立交匝道普遍采用30 km·h-1或40 km·h-1的设计速度；②在这两种设计速度条件下的通行能力差异较小.国内现行标准与美国的HCM均表明两者的差异一般不大于100 pcu·h-1·ln-1.同时，该模型各参数的显著性检验、t统计量均表现良好，满足5%置信度要求.同主线模型，本研究依次通过方差膨胀系数、K-S检验等对最终的匝道模型进行了检验.结果表明，匝道模型的方差膨胀系数为1.030(<10)且K-S检验P值为0.084(>0.05)，表明模型的拟合结果良好.

基于匝道验证组数据，计算匝道模型的通行能力预测误差，见图2.模型的误差在[-8.417%,8.203%]的区间内.对应的相对误差平均值(4.445%)、中位数(3.467%)、以及标准差(2.676%)，表明匝道模型的预测误差相对较低，泛化性良好但略低于主线模型.

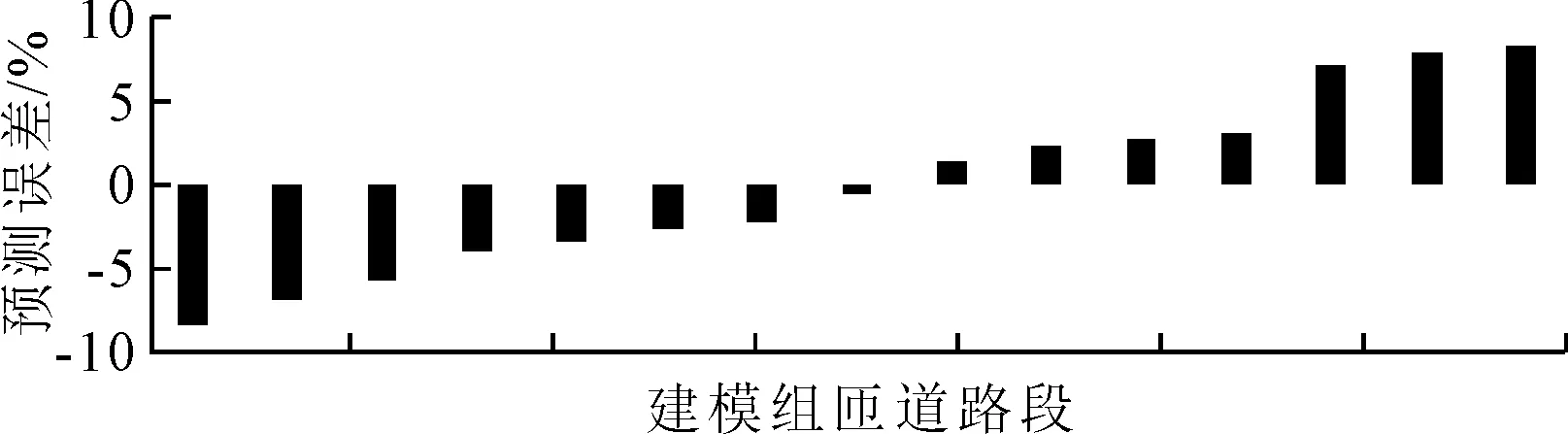
图2 匝道模型预测误差

3 结果分析

3.1 对比美国HCM

HCM中通行能力一般指在无平曲线、无竖曲线、坡度小于2%、且无大车等条件下的基本通行能力.

关于连续流状态的基本段，HCM将其分为两类：①完全控制出入且完全不受交通控制干扰的基本段，相应的设计速度区间为55～75 mi·h-1(1 mi·h-1≈1.609 km·h-1)；②部分控制出入，基本不受交通控制干扰，相应的设计速度区间为45～60 mi·h-1.在本研究中，低等级立交普遍存在于重庆市主城各区，导致重庆立交主线的连续流特征明显，如重庆市渝中区的主干路——菜袁路(设计速度为50 km·h-1，约为31.068 mi·h-1)，全长约4.2 km，共设有4座立交，无平面交叉口，其主线通行能力基本不受交通控制等因素的影响.将HCM中设计速度在45～50 mi·h-1内的第二类基本段通行能力作为补充，进行了同条件对比，见图 3.

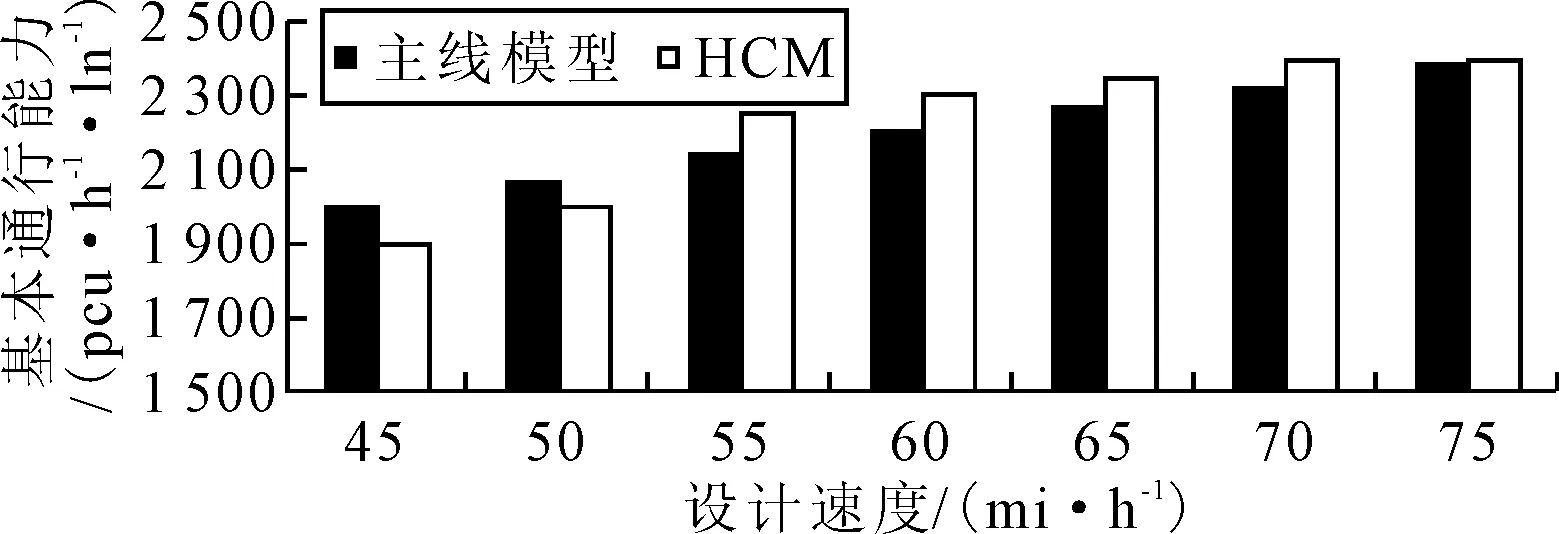
图3 主线模型与HCM对比

当设计速度不小于55 mi·h-1时，模型结果整体上略小于HCM建议值，但差距较小，且二者的差异随设计速度增大而减小.通常，设计速度与道路几何线型标准成正相关.在较低的设计速度下，山地城市的道路设计往往依山就势，受地形条件制约，设计者常采用较小的曲线半径、较大的纵坡等线型元素，使得山地城市与平原城市的道路线型存在明显差异.而在较高设计速度下，山地城市道路常采取修建桥梁、隧道等方式来满足较高等级道路的线型要求，因而与平原城市的道路线型差异较小，通行能力的差异也随之减小.如当设计速度为75 mi·h-1时，模型结果与HCM建议值之间仅存在19 pcu·h-1·ln-1的差距，仅占HCM建议值(2 400 pcu·h-1·ln-1)的0.792%，基本可忽略不计.

当设计速度小于55 mi·h-1时，HCM仅提供了部分控制出入的连续流通行能力建议值，其特点在于考虑了部分交通控制等因素对通行能力的微弱影响.因此，在该设计速度下，本研究模型计算结果略高于HCM建议值，如当设计速度为在45 mi·h-1时，模型结果是HCM的104.737%.

关于匝道通行能力，考虑到重庆市区立交匝道的设计规格相对单一，本研究仅对比了匝道模型结果与HCM的匝道通行能力建议值(设计速度区间为20～30 mi·h-1)的差异.结果表明，同等设计速度下山地城市的匝道基本段通行能力为1 664 pcu·h-1·ln-1，显著小于HCM建议的1 900 pcu·h-1·ln-1.该结果表明，山地城市特征因素对匝道通行能力的影响较为显著.

3.2 对比国内CJJ37

与HCM类似，CJJ37中的通行能力是指无平曲线、无竖曲线、坡度较小、且大车比例为0等条件下的基本通行能力.

在同等条件下，本研究模型结果与CJJ37建议值的对比见图 4.由图4可知：随着设计速度增大，主线模型与标准建议值的差值在逐渐减小.当设计速度为100 km·h-1时，主线模型计算结果与CJJ37建议值(2 200 pcu·h-1·ln-1)仅存在14 pcu·h-1·ln-1的差值，约占CJJ37建议值的0.636%，基本可忽略不计.上述对比结果类似于主线模型与HCM的对比结果.

当设计速度小于40 km·h-1时，山地城市特征因素对通行能力的影响较为明显，表现为设计速度越小，主线模型计算结果越低于CJJ37的建议值.当设计速度为30 km·h-1时，主线模型计算结果与CJJ37建议值的差值为154 pcu·h-1·ln-1，约占CJJ37建议值的9.625%.该结果表明，在较小设计速度条件下，山地城市与平原城市的道路线型差异明显，相应的通行能力差异显著.

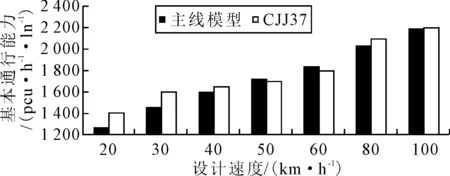
图4 主线模型与CJJ37对比

关于匝道通行能力，考虑到重庆市立交匝道的建设现状，对比了匝道模型计算结果与CJJ37中30或40 km·h-1设计速度下匝道通行能力值.其中，30 km·h-1设计速度对应的通行能力为1 600 pcu·h-1·ln-1，40 km·h-1设计速度对应的通行能力为1 650 pcu·h-1·ln-1.而在同等条件下，本研究匝道模型计算的通行能力为1 664 pcu·h-1·ln-1，略高于40 km·h-1设计速度下的通行能力建议值，两者的差值仅为14 pcu·h-1·ln-1，占CJJ37建议值的0.848%，基本可忽略不计.

3.3 对比重庆地标

重庆地标是基于国内CJJ37制定的，两者在不同设计速度下的通行能力建议值基本一致，仅当设计速度为80 km·h-1时，重庆地标的通行能力低于国标CJJ37，为2 000 pcu·h-1·ln-1，见图5.同等条件下，主线模型计算结果与重庆地标通行能力建议值对比结果所反映的趋势与前述对比国内外标准的结果基本一致.在80 km·h-1的设计速度条件下，模型计算结果与重庆地标建议值仅存在25 pcu·h-1·ln-1的差值，约占1.250%.

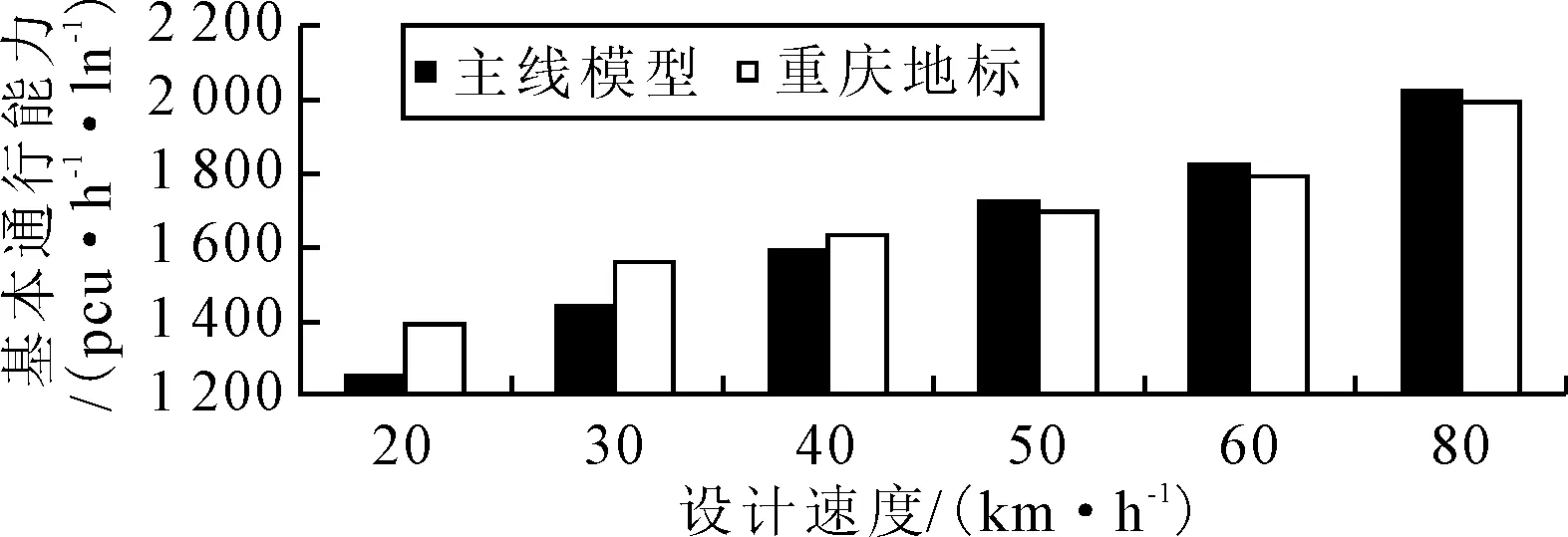
图5 主线模型与重庆地标对比

由于重庆地标采用了与CJJ37同样的标准，关于匝道通行能力的对比可参考本研究模型与CJJ37的比较结果.

4 山地城市立交基本段通行能力

通过对比国内外的通用通行能力标准可知，本研究建立的模型可较好的反映典型山地特征因素作用下的立交基本段通行能力与国内外通用通行能力建议值的差异.为方便设计人员使用，量化山地城市立交基本段通行能力，在无竖曲线、无平曲线、大车比例为0的条件下，给出了基于模型计算的通行能力建议值见表4.

表4 山地城市立交基本段通行能力建议值

5 结 论

1) 针对交通流数据的多元特征，通过马氏距离、KNN等算法等对采集得到的交通数据进行了数据挖掘、清洗等预处理，提出了异常数据的干扰，提高了统计分析模型的拟合精度，降低了模型的预测误差.主线模型的整体拟合精度及其平均相对误差分别为0.989、2.740%；主线模型的拟合精度及其平均相对误差分别为0.957、4.445%.

2) 主线立交的通行能力影响因素主要为圆曲线半径、竖曲线半径、设计速度、大车比例.而匝道立交的通行能力影响因素则主要为平曲线转角、竖曲线半径、大车比例.该结果出现的原因是山地城市立交匝道设计速度单一、匝道普遍具有小半径和大偏角的几何特征.

3) 与既有的国内外标准相比，本研究发现设计速度越大，山地城市立交基本段通行能力与标准建议值的差距越小.反之，山地特征对通行能力的影响越大，两者的差异越大.如同等条件下主线模型与CJJ37建议值的比较结果所示，设计速度为100 km·h-1时，模型结果与标准建议值基本一致，仅存在0.636%的差异，基本可忽略.而当设计速度为30 km·h-1时，上述两者之间则存在9.625%的差异.

4) 基于主线模型、匝道模型计算结果提出了适用于山地城市立交基本段的通行能力建议值.