双点式高速冲压机械振动控制研究
2023-01-18邱聪,高媛,钱峰
邱 聪,高 媛,钱 峰
(大连理工大学机械工程学院,辽宁 大连 116024)
0 引言
高速冲压机械广泛应用于航空航天、电子通讯、汽车制造等现代工程领域。适应提高产品质量及生产效率企业目标需求,冲压机械设计呈现精密性及高速化研究发展趋势。随着冲压行程次数的提高,导致高速冲压机械在冲压工作时不可避免地产生振动及噪声,严重影响滑块下死点动态性能,从而降低加工精度。因此进行高速冲压机械振动控制研究,对提高机械产品动力学性能进而提高产品质量具有重要意义。
文献[1]建立了单自由度冲压机械振动分析模型,针对高速压力机振动冲击进行隔振技术研究。文献[2]以曲柄滑块压力机为研究对象,建立双自由度有阻尼振动分析模型,仅考虑由惯性力载荷对隔振器参数进行优化设计。文献[3]以机身为研究对象,建立水平、垂直、扭转三自由度振动模型,并提出了综合平衡优化设计方案。文献[4]仅考虑冲压载荷作用,提出了三自由度集中参数动力学模型,分析机械振动机理。
本文以双点式高速压力机为研究对象,在高速冲压载荷作用下,压力机属于刚柔耦合多体系统。考虑惯性力与冲压载荷,基于集中参数法建立整机系统三自由度动力学模型,揭示振动机理,实现压力机动态特性定量分析。利用ADAMS进行近似对称机构平衡方案优化设计,实现控制振动提升机械动力学性能研究目标。分析框架如图1所示。

图1 振动控制分析框架
1 压力机动力学建模
图2为双点式高速压力机系统组成示意图。原动件曲轴1以角速度ω回转,构件2与2′为双连杆,构件3为冲压滑块。
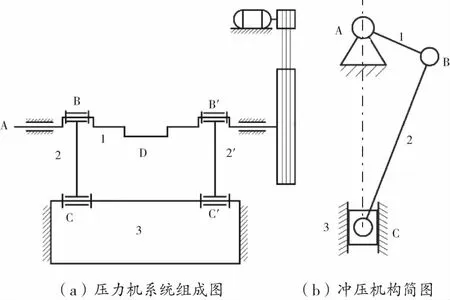
图2 高速压力机系统组成示意图
1.1 建立三自由度振动模型
采用集中参数法,建立更加符合实际工况的高速压力机动力学模型。在实际冲压加工时,滑块与连杆相连,滑块部件(M2)在短时间内受到巨大激振力F(t),使连杆产生瞬时大变形,因此将连杆视为弹性体(K2)。产生的激振力通过传动机构传递给曲轴,曲轴与上横梁部件(M1)连接,使机身产生弹性变形,因此将机身视为另一弹性体(K1)。压力机底座(M3)通过隔振器(K3)与大地连接,将多余的弹性势能传递给基础。依据以下假设:
(1)仅考虑压力机系统竖直方向振动;
(2)将系统滑块、曲轴、底座视为刚性质量块;
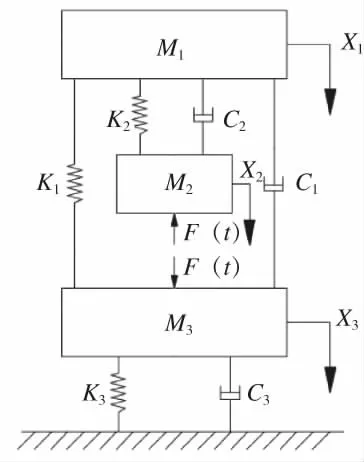
图3 三自由度振动模型
(3)各运动副均为无间隙刚性连接。
建立上横梁X1、传动机构X2、底座X3三自由度振动模型,如图3所示。
取压力机竖直向下为正方向,根据牛顿-欧拉矢量力学法,将各个质量块从机器系统中独立出来,各集中质量块的受力分析图如图4所示。
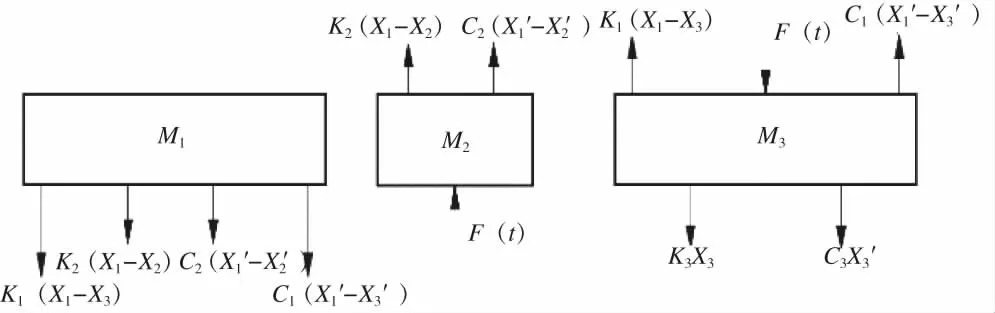
图4 各集中质量块受力图
1.2 求解振动微分方程
根据各集中质量块受力分析图,采用式(1)将压力机动力学模型描述为振动运动微分方程,定量分析系统振动特性。其中弹簧以变形能储存能量,而阻尼以机械能削减能量。

(1)
压力机在工作时受到的激振力主要由冲压力F(t)和周期性惯性力组成,冲压力表达式如下:

(2)
其中惯性力由运动部件产生,通过质量代换法将连杆质量等效转移到曲柄和滑块上。曲柄作回转运动产生离心惯性力,滑块作直线运动产生往复惯性力,合惯性力在竖直方向分量为meω2sinωt。由此可得压力机三自由振动运动微分方程为:
(3)

利用高精度的龙格库塔法求解压力机系统的振动运动微分方程,首先将微分方程从高阶转换为低阶,然后利用MATLAB仿真得到系统的振动响应规律。
设初始条件为:
(4)
假定状态变量为:
(5)
将式(3)改写为如下一阶微分方程组的形式:
(6)
利用SolidWorks测算压力机关键零部件质量参数;利用ANSYS求解机身、连杆的刚度值,根据阻尼比求得相应阻尼;选取隔振器的刚度和阻尼值。由此得到振动模型各参数值,如表1所示。

表1 振动模型各参数
1.3 振动分析结果
取主轴转速300 r/min,求解得压力机各部分振幅,如图5所示。
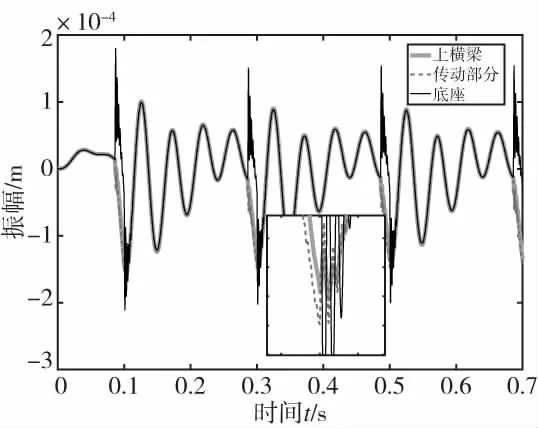
图5 冲压时各部分振幅
根据图5可知,在冲压时,底座振幅较大,上横梁振幅较小。并且压力机在冲压前仅受惯性力的影响,振幅较小,当受到冲压力时,压力机的振幅发生瞬间突变。
1.4 振动影响因素定量分析
1.4.1 传动机构周期惯性力
由于惯性力与主轴转速的平方成正比,现分别选取不同的主轴转速,利用MATLAB进行数值仿真,求解压力机在空载时仅受不平衡惯性力的作用下,各集中质量块的振幅仿真结果如图6所示。
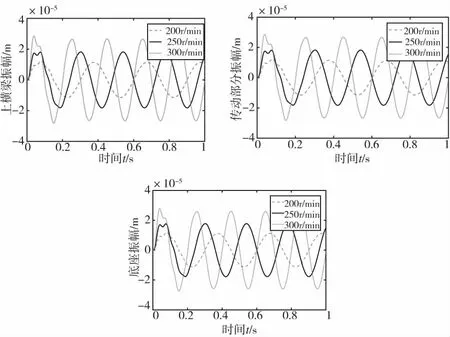
图6 不同惯性力下各部分振动波形图
1.4.2 瞬时冲压力
除去不平衡惯性力会引起压力机振动外,冲压力也是引起压力机振动的主要原因之一。现分别取不同的冲压力F(t),利用MATLAB进行数值仿真,求解得压力机在冲压时受到激振力的作用下,各集中质量块的振幅仿真结果如图7所示。

图7 不同冲压力下各部分振动波形图
根据图6和图7可得以下结论:
(1)机构惯性力导致传动部分振幅较大,底座振幅较小。随着主轴转速的提高,惯性力的不断增大对压力机振动的影响十分显著。
(2)高速压力机惯性力和冲压力合成的激振力促使底座产生较大振幅,机器各部分振幅随着冲压力提高也相应的增加。
(3)机构惯性力和冲压力都是导致高速压力机振动的关键因素。冲压载荷取决于冲压工艺及板料性能。本文基于机械结构优化设计,重点研究降低高速机构惯性力,提高机构动力学性能。
2 机构平衡优化设计
机构平衡设计可采用附加质量和附加平衡机构以完全或部分平衡机构周期变化惯性力,提高机械动力学性能[5]。高速压力机应用近似对称布置附加机构方法,平衡机构如图8所示。
2.1 优化设计目标函数
通过优化平衡机构的特征参数,减小高速压力机在工作时所产生的不平衡惯性力,从而降低压力机的振幅[6]。以运动部件对主轴竖直方向Fy和水平方向Fz惯性力变动量加权和最小为优化目标函数,其表达式如下:
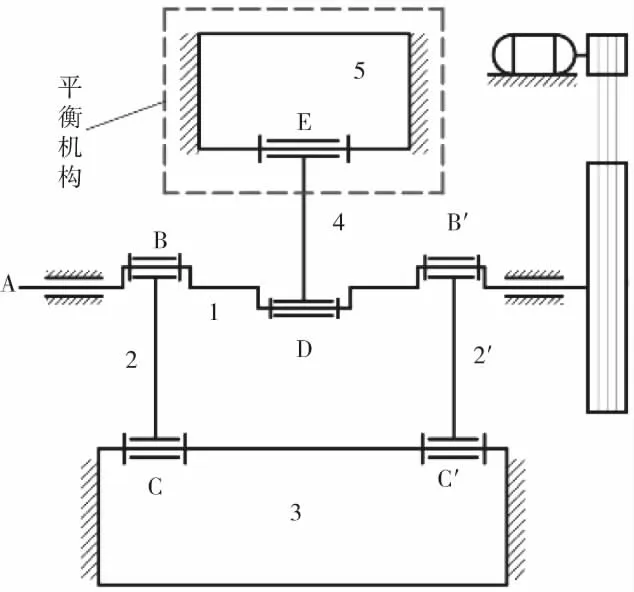
图8 机构平衡设计示意图

(7)
其中主要考虑竖直方向的振动,取加权系数为μ1=0.7,μ2=0.3。
2.2 优化变量及约束条件
以附加平衡机构连杆4及滑块5质量为优化变量。综合附加平衡机构的紧凑性与合理性,其优化设计约束条件如下:
(8)
2.3 建立ADAMS仿真模型
建立ADAMS高速压力机参数化仿真模型,如图9所示。传动系统各构件间通过正确的约束连接,并且去除冗余约束,在主轴上施加驱动载荷,设定目标函数及优化变量,对高速压力机模型进行仿真试验,机构平衡仿真优化设计流程见图10。

图9 压力机参数化仿真模型
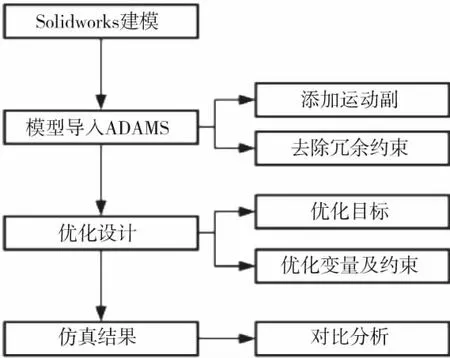
图10 机构平衡仿真优化设计流程图
2.4 优化结果分析
在ADAMS中,重复进行仿真试验。根据ADAMS生成的优化设计报告,提取目标函数最小时所对应的优化变量值,即为最优结果,取m3=36.506 kg,m4=2.5436 kg。
将高速压力机优化后的参数代入仿真模型中,对比优化前后的动力学特性。分别取主轴转速为200 r/min、250 r/min、300 r/min,利用ADAMS后处理模块,测得运动部件对主轴惯性力优化前后的对比如表2所示。
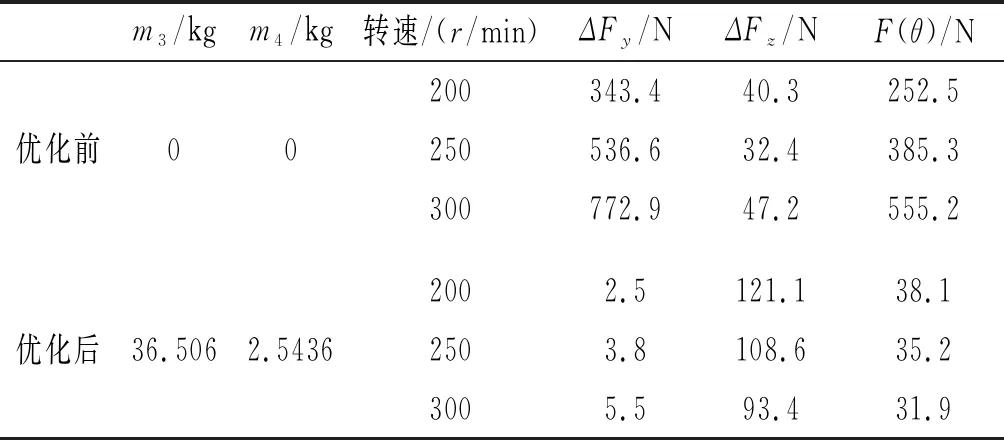
表2 优化前后惯性力性能对比
根据表2优化前后惯性力对比可知,随着主轴转速的提高,Y方向惯性力增大十分明显。但添加平衡机构后,竖直方向的惯性力比优化前降低1%左右,可忽略不计。表明近似对称布置法对高速压力机惯性力的平衡效果非常显著。
将优化后的平衡机构参数代入振动方程中,在空载条件下,以上横梁振动为例,对比分析平衡前后振幅值,如图11所示。
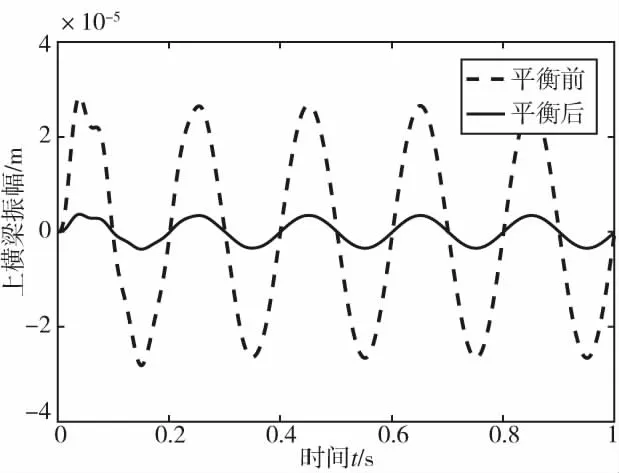
图11 上横梁振动波形图
平衡前,上横梁的振动峰值为2.815×10-2mm;在进行惯性力平衡后,上横梁的振动峰值降低为3.702×10-3mm,降低幅度为86.8%。因此,此附加平衡机构的方案,可以有效降低高速压力机的惯性力,从而实现减振效果。
3 结论
1)应用集中参数法建立高速压力机刚柔耦合多体系统三自由度动力学模型,定量分析振动影响因素揭示振动机理,为高速压力机振动控制提供理论指导。
2)针对机械系统振动主要因素机构不平衡惯性力,进行机构平衡优化设计以降低振动。以附加平衡机构滑块及连杆质量为优化变量,以运动部件对主轴竖直方向Fy和水平方向Fz惯性力变动量加权和最小为优化目标函数,利用ADAMS仿真求解最优方案。分析结果表明,机构平衡优化设计可改善机械动力学性能,达到控制压力机振动响应的目的。
