运用代理模型的超低温阀优化设计*
2023-01-18方宇豪王守真王林涛
方宇豪,王守真,王 帅,王林涛
(1.大连理工大学机械工程学院,辽宁 大连 116024;2.大连船用阀门有限公司,辽宁 大连 116024)
0 引言
近些年,我国的航天等产业发展迅速,伴随着这些产业的发展,对于各种特殊介质的储存、运输等也有着越来越高的要求,LNG作为其中一种重要的能源,也需要相应的流体控制设备,超低温阀在其中扮演着相当重要的角色,而对于超低温阀的设计制造等也提出了越来越高的要求[1]。
超低温阀(如图1)是由阀体、阀盘、阀盘压套、阀盖、阀杆、填料垫、填料、填料压套、支架和管道组成。由于超低温阀的工作环境较为恶劣,流通介质特殊等特点,会产生密封不严、流阻过大等问题,故而对超低温阀门的设计制造等提出了较高的要求。因此,有必要在满足强度、密封性条件下对超低温阀进行结构优化设计。
我国对超低温阀的研究开始于20世纪90年代,鹿彪等探讨了超低温阀门的一些结构,分析了超低温阀门的材料和实验[2]。丁强伟对LNG用超低温截止阀做了热固耦合分析,分析了超低温阀门的应力场[3]。杨刚等研究了超低温球阀的主密封副性能,提出了改善主密封副性能的方法[4]。王宇峰针对闸阀的工作条件进行分析,针对分析结果对闸阀的密封性能提出了一定的改进意见[5]。在这些研究中,不乏针对超低温阀门进行结构优化的,但是使用的方法较为简单。
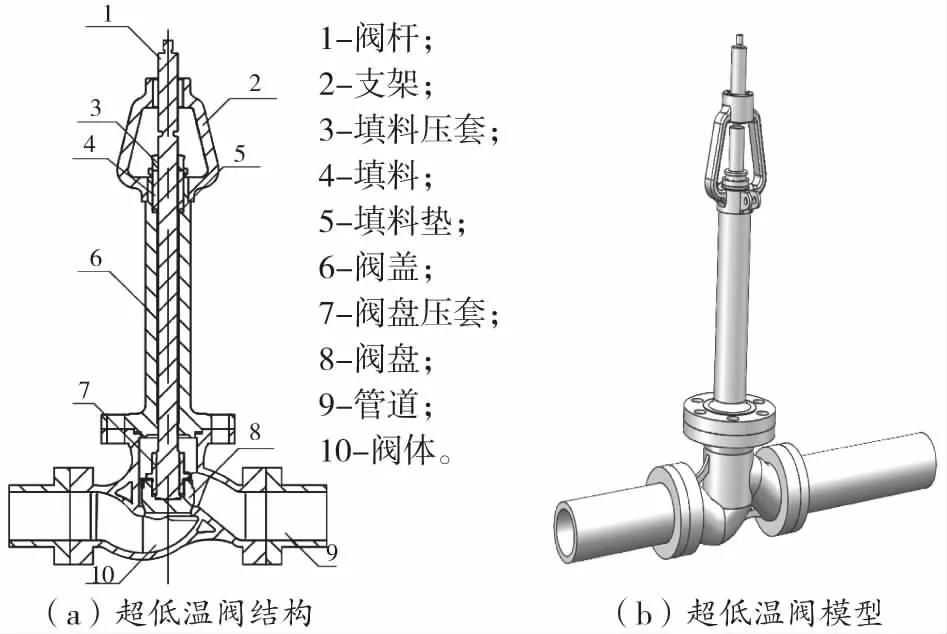
图1 超低温阀
以往的优化设计往往是通过有限元方法进行的,但是有限元方法耗费的时间一般比较长,为了解决这个问题,现在的研究中会使用代理模型方法来代替有限元模型来提高计算效率[6]。其中,Kriging模型在解决高维非线性问题时性能较好,使得Kriging模型在工程问题中的应用越来越广泛[7]。本文通过构建高精度的代理模型,来探究对阀门结构的减阻优化。
1 参数化建模与有限元分析
1.1 参数化建模
通过SolidWorks分别建立阀门各个零件的参数化模型,如图2所示。选用的为DN50的超低温截止阀,额定工作压力2 MPa,进口流速5 m/s,额定工作温度-162 ℃。为了消除管道长度对流体特性的影响,经过测试,在开启工况时采用入口处管道长度为4倍通径,出口处管道长度为8倍通径。在不改变装配尺寸的前提下共对该装配体设置102个参数。其中,有76组参数之间互相关联,最终作为独立变量的参数共有26个,将这些作为独立变量的参数标注在对应的模型上,进行参数化建模,如图2所示。各个设计变量的参数以及范围见表1。
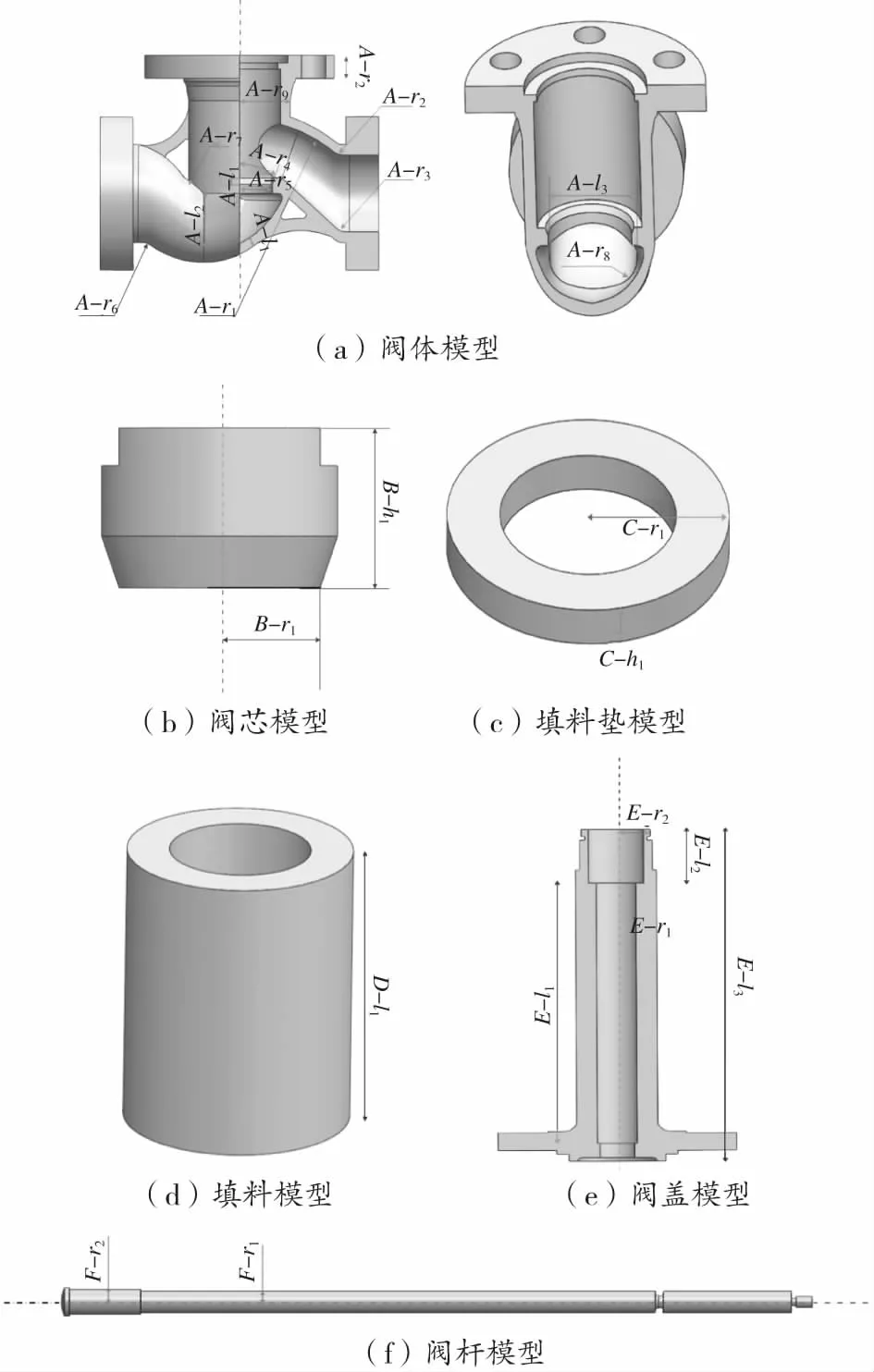
图2 阀门零件参数化模型
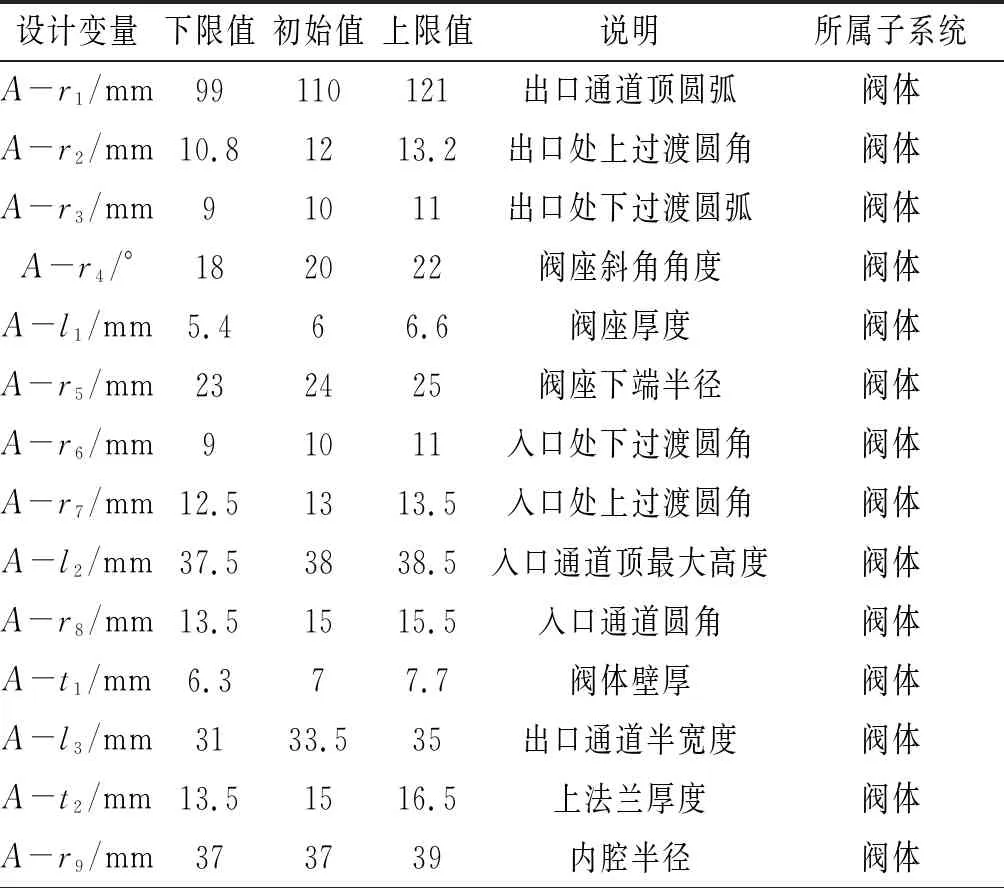
表1 设计变量

续表1
1.2 有限元仿真
1.2.1 载荷分析
超低温阀门在开启和关闭的瞬间受到的载荷影响最大,因此要对关闭瞬间的阀门工况进行分析。超低温阀门关闭时受到的载荷主要有以下三个方面:阀门零件间相互的结构应力、介质压力、温度场产生的热应力。
Ⅰ.填料与阀杆间的摩擦力
QF=πdFhZ1.2PfsinαL
(1)
其中,h是单圈填料的高度,Z为填料的圈数,f为填料与阀杆间的摩擦系数(约为0.05),αL为阀杆螺纹的螺旋角,填料与阀杆间的摩擦力为381.2 N。
Ⅱ.介质作用力
介质从阀盘下方流入时,阀门密封面总共受到了介质静压力和介质密封力:
QMZ=QMJ+QMF
(2)
其中,QMJ为密封面上的介质静压力。
(3)
其中,DMN为密封面内径,bM为阀座密封面宽度,P为计算压力。计算得QMJ为4085.6 N。
而QMF是介质密封力,对于锥面密封而言
(4)
其中,DMW为密封面外径,α为锥面半角,fM为密封面摩擦系数(取0.2),qMF为密封比压。
(5)
查表得约为6 MPa。计算得QMF为2385.3 N。因此总介质作用力为:
QMZ=4085.6 N+2085.3 N=6470.9 N
(6)
Ⅲ.热应力
根据设计规范,工作温度下密封面上产生的平均热应力为10 MPa,定义热应力的作用方向总是与阀门密封力方向相反。即:
(7)
考虑极限情况下填料与阀杆摩擦力、介质作用力、热应力均与密封方向相反,因此预紧力计算公式:
F=QF+QMZ+QT=9993.7 N
(8)
为留有一定余裕且方便计算,将其取为10000 N。
1.2.2 有限元仿真
建立好的参数化模型导入到ANSYS Workbench分别进行热固耦合分析与流体分析,阀门材料主要采用奥氏体不锈钢,流体部分采用液氮,材料信息见表2。

表2 材料属性
对于热固耦合分析而言,首先生成网格,总体采用5 mm四面体网格,密封面处精度要求较高,采用1 mm网格细化处理,并且采用边界层,共生成单元数557764,节点数883141。阀盘与阀体的密封面设为摩擦接触,摩擦系数0.2。将阀杆与阀盖、阀杆与填料间设为不分离。阀体部分设为-162 ℃,上阀盖部与空气接触,室温29 ℃,对流换热系数为15 W/(m2·℃)。阀体上法兰与进出口采用位移约束,阀体内部工作压力为2 MPa。对于流体分析而言,首先生成网格,总体采用10 mm四面体网格,在结构变化不平缓处采用1 mm网格细化处理,并且采用边界层,共生成单元数315210,节点数108150。流体部分采用速度入口5 m/s,压力出口2 MPa。设置见图3。

图3 参数设置
2 仿真结果分析
2.1 应力仿真结果
阀门应力仿真的结果见图4,收到了温度场和介质作用力的共同影响,阀门的热应力主要在阀体内腔,其中在接近上法兰位置达到最大值,而在其他结构处的应力较小。从图4可以看出,在阀体内腔处的应力值大约在50 MPa到70 MPa之间,而低温阀门所用的材料CF3M的屈服强度是243 MPa,远远小于材料的屈服强度。同时,阀门的最大应力出现在靠近上法兰的流道处,达到了105 MPa,此处不止有在约束边界处的应力奇异,还包括结构的不连续而产生的局部应力集中,属于正常现象,在可接受的范围内。为了避免密封结构失效,应保证密封比压在一定的范围内,最大密封比压为23.5 MPa小于许用密封比压40 MPa。但是平均密封比压为3.08 MPa,低于达到密封效果的最低密封比压,因此可能会发生密封失效。

图4 应力仿真结果
2.2 流体仿真结果
阀门流体仿真的结果如图5。阀门的流阻系数主要取决于进出口的压力降与流体的平均流速,而在该超低温截止阀的工作状态下,阀门内腔的一些流通截面变化较大处与壁面的影响会对平均流速的影响较大。此次结果平均流速达到了5.19 m/s,且在一些细小截面处最大流速达到了18.8 m/s。因此对于往后要做的设计中应当充分考虑结构对于介质平均流速的影响。

图5 流体仿真结果
3 Kriging模型
有限元方法分析虽然结果较为精确,但是耗费的时间过长,不利于一些参数较多的非线性问题,因此,可以利用代理模型方法。通过构建超低温阀门的Kriging模型来代替有限元仿真去进行优化设计。
首先进行试验设计来构建设计变量空间(S,ys),S=[x(1),x(2),…,x(n)]代表n行设计变量,ys=[y(x(1)),y(x(2)),…,y(x(n))]T代表n组输出值,并且S与ys之间是一一对应的关系。而Kriging模型[7-8]可以看作是一种特殊的径向基模型,因此可以用径向基函数来表示:
(9)
对于该基函数的权值,可以利用高斯随机分布来计算,即将其视为一个高斯随机过程:
Y(x)=β0+Z(x)
(10)
其中,β0表示为Y(x)的均值;Z(x)可以看作方差为σ2,均值是0高斯分布。设计空间中每组变量之间可以用基函数来表示关联性:
Cov[Z(x),Z(x′)]=σ2R(x,x′)
(11)
在此,可以通过使y(x)值均方差最小的方法来得到式(9)中的权值ω,即:
(12)
最小,并且Kriging模型应使响应值满足无偏估计:
(13)
在此基础上,利用拉格朗日乘数法求得模型的预测值和均方差:
(14)
(15)
其中,F是一个n×1阶的单位列向量,
β0=(FTR-1F)-1FTR-1ys,
r=[R(x(1),x),…,R(x(n),x)]T。之后求取极大似然函数,从而得到式(11)所需的θ值:
(16)
为了使构建完成的Kriging模型更加符合原有限元模型,应当保证其有足够的精度,因此在设计抽样方案时应使样本尽量具有代表性[9]。通过最优拉丁超立方抽样法完成抽样,分别得到800个训练样本和200个测试样本。选择相关系数r2作为代理模型精度衡量标准,要求其不小于0.9。最终,构建出阀门最大应力、最大变形量、密封比压、填料底部最低温度和流阻系数的Kriging模型,代理模型验证结果如图6所示。从图6可以看到,平均密封比压模型精度略低,但是相关系数r2仍然在0.9之上,满足要求。

图6 代理模型验证结果
4 优化结果
4.1 建立优化数学表达式
根据设计规范与使用要求建立优化数学表达式。阀门的材料选用奥氏体不锈钢,屈服强度为243 MPa,要求阀门正常工作时的最大应力不超过屈服强度。根据工作规范,阀门正常工作时,最大变形量应小于1 mm。为保证密封面的密封效果,应使密封比压保持在许用密封比压之内,根据工作规范,许用密封比压的范围为6 MPa≤[σ]≤40 MPa,填料底部的温度应该在0 ℃之上。综上所述,以阀门的流阻系数为优化目标,优化数学表达式为:
findx=[x1,x2,x3,…,x26]T
minK(x)
g1=T-t1≤0
g2=σN-[σ]≤0
s.tg3=D-Dmax≤0
g4=[f1-fmin][f1-fmax]≤0
xD≤x≤XU
(17)
其中,设计变量x的取值范围应该为[xD,xU]。
4.2 求解
建立完优化数学表达式之后,下一步应该寻找最优解。为了避免局部收敛或者求解精度低,找到全局搜索与局部发掘的平衡点,最终选择一种由MIGA(多岛遗传算法)与NLPQL(非线性二次规划)相结合的组合算法[10]。该组合算法是结合了两种算法的长处,首先通过MIGA确定最优解所在的设计空间,然后通过NLPQL在这个区域内寻优,以此得到全局最优解。
使用组合算法的优化过程如图7所示。从图7可以看出,优化目标收敛于4.882,g1收敛于0.54 ℃,g2收敛于101.19 MPa,g3收敛于0.955 mm,g4收敛于6.15 MPa。函数初始值和最优解如表3所示。

图7 迭代过程
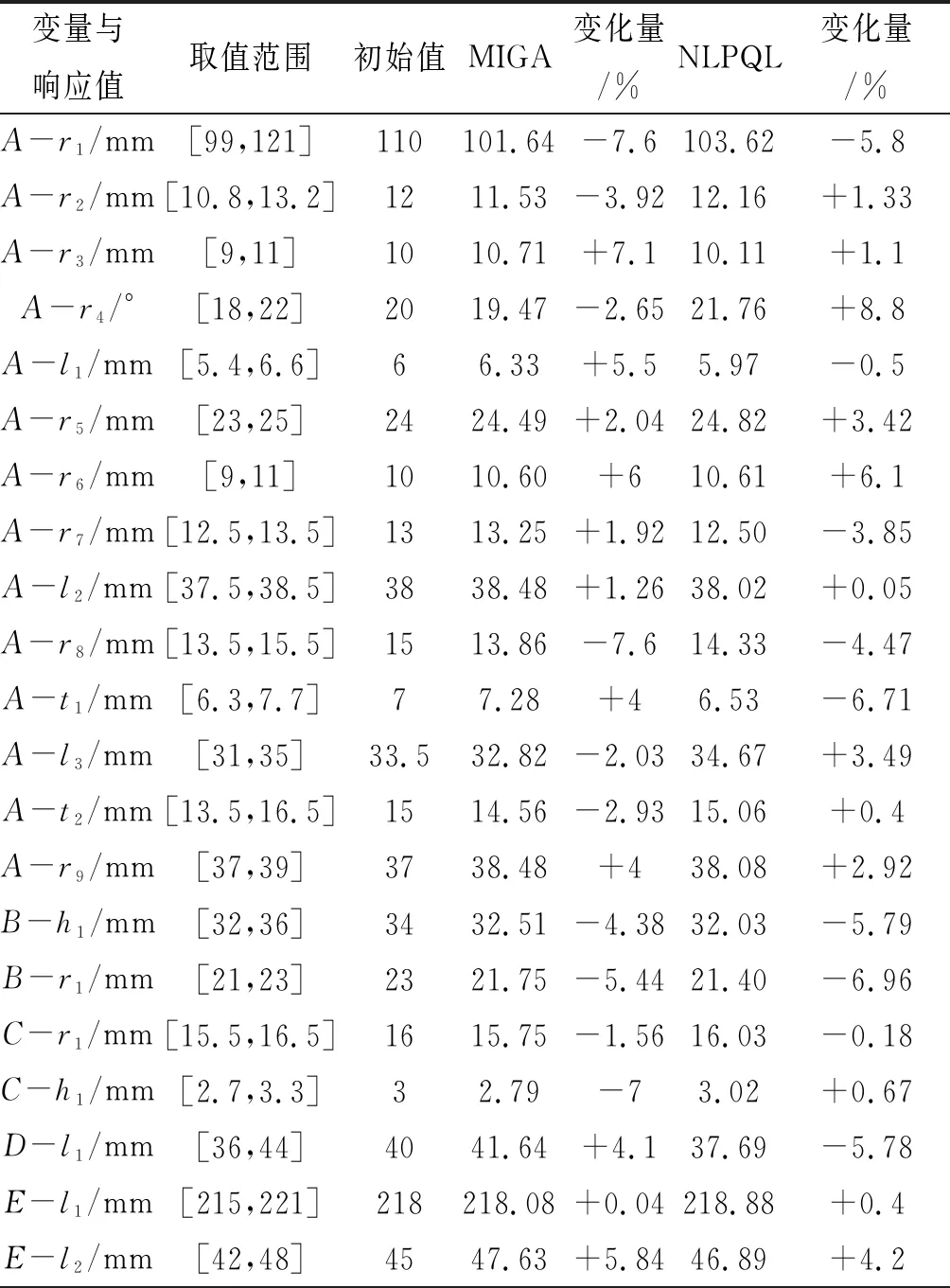
表3 初始值和最优解对比
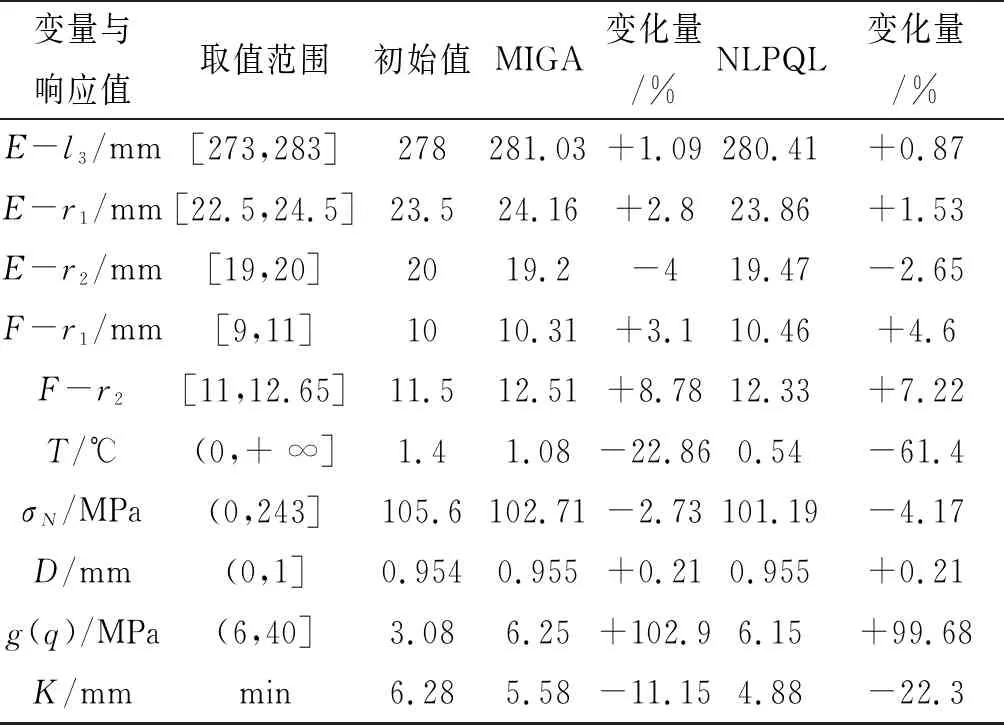
续表3
可以看到,在MIGA全局搜索之后,相较于初始值最大应力减少了2.73%,填料底部最低温度减少了22.86%,最大变形量增加了0.21%,密封面平均密封比压增加了102.9%,阀门流阻系数减少了11.15%。利用NLPQL进行局部寻优之后,相较于初始值最大应力减小了4.17%,填料底部最低温度减少了61.4%,最大变形量增加了0.21%,密封面平均密封比压增加了99.68%,阀门流阻系数减少了22.3%,从6.28变为4.88,减小了1.4。
分别将迭代后得到的设计变量与响应值代入到原有限元模型中,对比优化目标值与仿真输出值之间的差距,并且得到它们之间的相对误差,从而验证优化结果是否准确,见表4。从表4可得,相比于仿真结果,最终优化结果的相对误差分别为1.37%,2.77%,-0.21%,0.33%和0.21%。虽然最大应力的相对误差略高,但是约束g2还远远未到约束边界,2.77%的误差不会发生失效。因此,Kriging模型的准确度较好,最终优化结果可信。
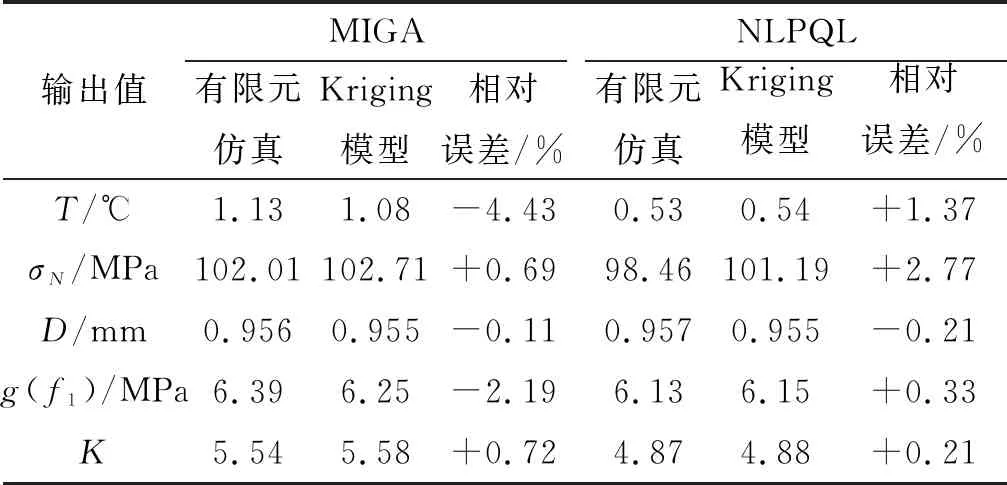
表4 结果对比
5 结束语
通过确定性优化减轻了超低温阀门的流阻系数,并且确定了其设计变量的设计值,得出了以下结论:
1)超低温阀门共有26个设计变量,并且经过分析后确定了其可能出现的失效形式。首先对超低温阀门的各个零件进行参数化建模,最终确定了26个参数作为设计变量开展下一步工作。分别运用有限元进行了热固耦合仿真与流体仿真,结果表明其密封比压在工作时易达到下临界点从而发生失效,因此需要在设计中充分考虑。
2)构建了高精度代理模型。传统的优化方法对其进行结构优化效率过低,因此构建了Kriging模型作为代替有限元模型来提高优化效率,并且通过拉丁超立方选取实验点,验证了代理模型的精度均在0.9以上,符合精度要求。
3)进行优化设计,使超低温阀的流阻系数降低了22.3%。根据优化目标以及约束条件构建优化方程,通过将MIGA与NLPQL结合的组合算法来进行全局寻优。最终的优化结果表明,流阻系数减小了22.3%,Kriging模型与有限元仿真结果的最大相对误差为2.77%,说明代理模型的优化结果准确度较高。
