单目机器视觉误差概率建模与分析
2023-01-17周金宇程锦翔
尹 鑫,周金宇,程锦翔
(1.江苏理工学院 机械工程学院,江苏 常州 213001;2金陵科技学院 机电工程学院,江苏 南京 211169)
近年来,机器视觉凭借其测量精度高、适应能力强、效率高等优势得到了广泛的应用,许多学者对此进行了研究。其中,大量的研究集中在相机的标定[1-4]、像素级边缘检测算法、亚像素边缘检测算法[5-7]和角点检测算法等方面;但是,对机器视觉测量误差的定量研究较少。
影响机器视觉测量误差的因素有光照、随机噪声、测量距离、观测角度、相机畸变和边缘检测算法等。外界光照的变化会导致到达每一个像素的光子数的变化,最终引起像素灰度值的改变,从而产生测量误差。噪声会影响图像边缘检测的质量,图像的噪声类型比较多,常见的噪声[8]主要有高斯噪声、泊松噪声和椒盐噪声。采用滤波的方式可以降低噪声对图像的影响;但是,噪声和边缘都属于图像中的高频部分,所以滤波同时也会导致边缘出现模糊。如何在降低噪声影响的同时保留高质量的边缘是一个难点。测量距离的变化会导致像素当量的改变,进而改变最终的测量结果。观测角度的波动也会导致测量结果的改变。相机畸变[9-10]分为径向畸变、偏心畸变和薄透镜畸变,和切向畸变相比,薄透镜畸变与径向畸变相对较小,可以不予考虑。目前,主要通过相机标定与畸变校正来减小畸变对图像的影响;但是,畸变校正后仍存在误差[11]。边缘检测算法主要分为传统边缘检测算子、新型边缘检测算子以及亚像素边缘检测算子。传统边缘检测算子有Roberts算子、Sobel算子、Kirsch算子、Laplacian算子、LOG[12]算子与Canny[13]算子等。新型边缘检测算子有小波变换方法、基于数学形态学的边缘检测方法等。亚像素边缘检测算子主要分为基于拟合的亚像素边缘检测算法、基于矩的亚像素边缘检测算法和基于插值的亚像素边缘检测算法。
本文综合考虑正常工作时间内外界光照变化、随机噪声和观测角度变化等因素,并针对现有典型的单目机器视觉测量技术,建立机器视觉测量误差概率模型。
1 坐标变换
在采用机器视觉测量技术进行高精度测量之前,首先要进行相机标定,得到相机的内参和外参。摄像机在成像变换过程中涉及到世界坐标系(Xw,Yw,Zw)、相机坐标系(Xc,Yc,Zc)、成像坐标系(x,y)以及像素坐标系(u,v)。为了确定相机在空间的位置,通过旋转矩阵R和平移矩阵T将坐标位置由世界坐标系转化成相机坐标系,两坐标系之间的变换式为:

式中:R为3×3正交单位矩阵;T为3×1平移矩阵。
成像变换过程中涉及到四个坐标系,物体实际点与成像点之间的投影关系如图1所示。
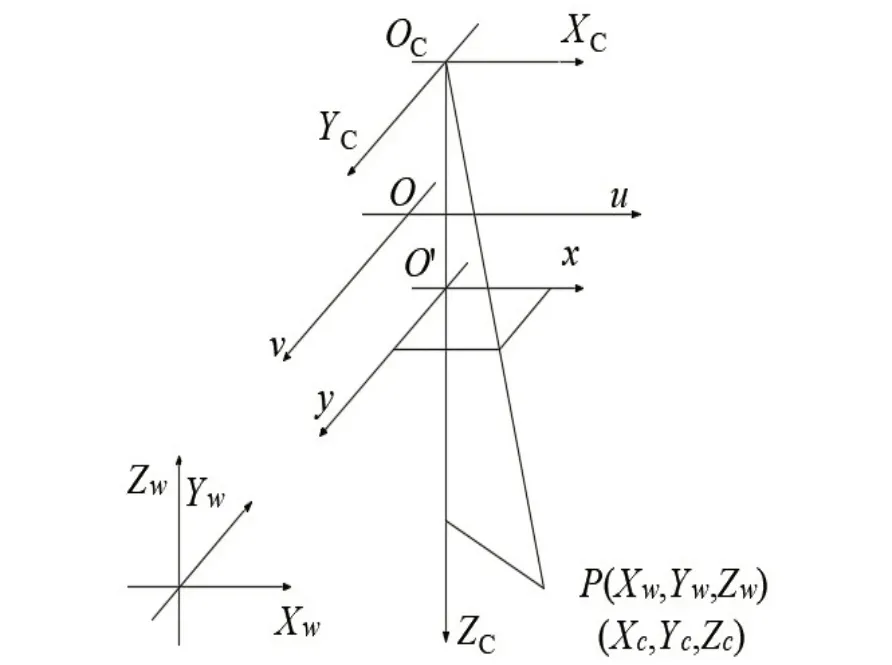
图1 成像线性模型
图像物理坐标系下图像坐标的单位为mm,图像像素坐标系下图像坐标的单位为pixel。图像物理坐标系和图像像素坐标系在同一平面中,两个坐标系之间的关系如图2所示。

图2 图像像素坐标系
若空间中一点P在世界坐标系中的齐次坐标为(Xw,Yw,Zw,1),在摄像机坐标系中的齐次坐标为(Xc,Yc,Zc,1),根据图像像素坐标系、成像坐标系、相机坐标系和世界坐标系之间的转换关系[14-15],像素坐标系和世界坐标系之间的变换式为:
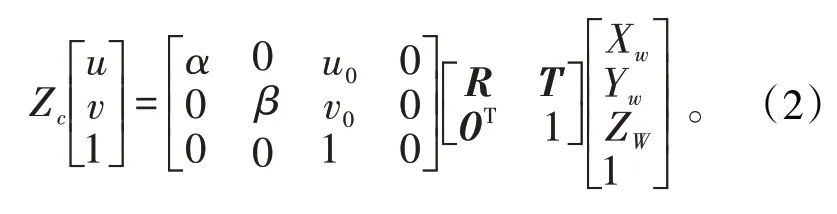
式中:α=f/dx,β=f/dy代表等效焦距;f为焦距;dx和dy分别为每个像素在成像坐标系x轴和y轴方向上的物理尺寸;(u0,v0)为光学中心坐标;O为3×1零矩阵。
大多数光学系统的成像是不完善的,导致拍摄的图片存在畸变,当考虑图像的径向畸变和离心畸变时,现实坐标和理想坐标之间的关系可以表示为:

式中:
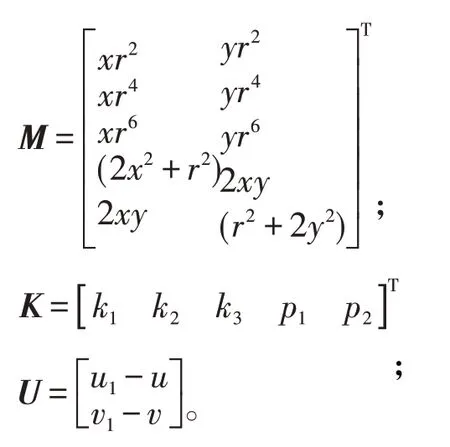
其中:r2=x2+y2表示图像中任一点到畸变中心点距离的平方;x=u-u0;y=v-v0;(u,v)为理想图像位置;(u1,v1)为实际图像位置;k1、k2、k3为径向畸变系数;p1、p2为切向畸变系数。
2 单目机器视觉尺寸测量建模
在采用单目机器视觉技术测量待测零件尺寸时,噪声是不可避免的:首先,在将光子转化为电荷的过程中,光子被光电二极管收集时会产生噪声,发热和半导体制造工艺的缺陷会产生暗电流噪声;其次,在将电荷转化为电压的过程中,真实传感器中电荷到电压转换的不完美会造成源跟踪噪声、传感节点复位噪声和偏移固定模式噪声;此外,在将电压转化为数字信号的过程中,模数转换器将电压转换成离散编码时也会带来非线性噪声。采用滤波的方式可以降低噪声对图像的影响,常用的滤波方式是高斯函数低通滤波,其表达式为:
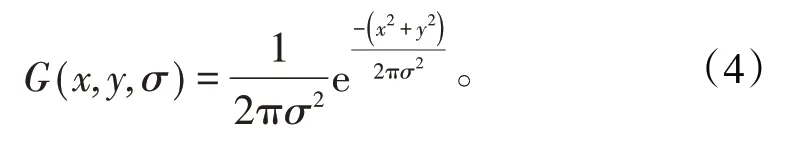
式中:σ为高斯空间系数;x2+y2表示高斯滤波的滤波核中任一元素到滤波核中心元素距离的平方。
图像的边缘展现了其基本信息,沿着边缘方向像素的灰度值变化缓慢,而垂直于边缘方向像素的灰度值变化剧烈。采用LOG(高斯拉普拉斯)算子对图像进行处理,边缘点位置为卷积图像二阶导数产生过零点的位置。由于图像沿梯度方向的二阶导数是非线性的,计算量较大,Marr提出用拉普拉斯算子替代,采用高斯滤波处理后的平滑图像g(x,y)的二阶方向导数图像

的过零点作为图像的边缘点。LOG算子的表达式为:

边缘检测后得到所有满足LOG算子的边缘像素点。对边缘上的像素点分别采用最小二乘法拟合,以边缘上每一个像素到边缘直线的误差平方和最小为目标,得到最佳边缘。已知边缘上的n个像素点(x1,y1),(x2,y2),…,(xn,yn),采用最小二乘法拟合出边缘直线。
考虑边缘厚度和边缘连续的因素,将超出厚度范围的像素点和与边缘不连续的像素点去除,从已知的n个像素点中剔除异常点,得到m个剩余像素点。将剩余的m个像素点(x1,y1),(x2,y2),…,(xm,ym)再次采用最小二乘法拟合,得到最终的边缘。
像素当量表示为:

式中:L1为待测零件某位置的像素长度;l1为采用三坐标测量仪检测相应位置所得到的长度,单位为mm。
测量误差函数定义为:

式中:L2为机械零件待测位置的像素长度;l2为采用三坐标测量仪检测相应位置所得到的长度,单位为mm。
3 蒙特卡洛模拟
影响单目机器视觉测量误差的因素有很多,如:外界光照变化、随机噪声、观测角度变化、测量距离变化、相机畸变、边缘检测算法,等等。一般在采用机器视觉技术测量机械零件尺寸时,测量距离保持不变,并且测量的精度较高。目前,对相机标定和畸变校正的研究较多,本文不再阐述。LOG算子属于优秀的边缘检测算子,其检测精度较高,引入的误差较小。本文主要研究光照变化、随机噪声和观测角度变化这三个因素对测量误差的影响,并且这三个因素会造成测量结果的分散性。
采用泊松噪声[16]模拟外界光照变化对图像产生的扰动,泊松分布的概率函数为:
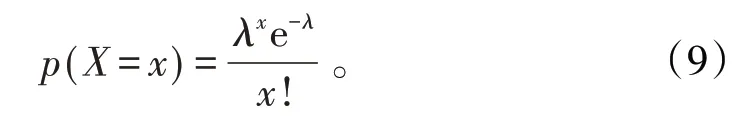
采用高斯噪声[16]模拟图像中的随机噪声,高斯噪声服从正态分布,正态分布的概率密度分布函数为:
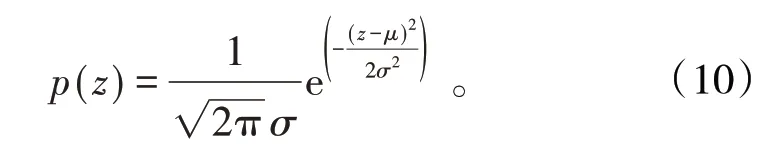
假设观测角度服从均匀分布,均匀分布的概率密度函数为:

假设这三个随机变量相互独立,采用蒙特卡洛法[17]计算单目机器视觉尺寸测量误差分布,具体步骤如下:
(1)根据式(3)并结合相机标定得到的内参和畸变参数,在理想图像中加入畸变;
(2)根据式(9)对畸变图像加入泊松噪声,根据式(10)对畸变图像加入高斯噪声,令观测角度服从区间(0°,1°)上的均匀分布;
(3)根据式(4)对图像进行高斯低通滤波,并输出滤波后的平滑图像;
阳性一方接受HAART且病毒载量达到持续抑制是HIV单阳家庭备孕的关键,另外,为了提高受孕成功率,准确计算排卵期非常重要,可以寻求妇产科医生的帮助。
(4)根据式(6)对平滑图像进行边缘检测;
(5)采用最小二乘法拟合边缘,将超出厚度范围的像素点和与边缘不连续的像素点去除后,再次采用最小二乘法拟合;
(6)根据式(7)和式(8)计算出测量误差;
(7)判断运算次数是否达到M次,若达到,执行下一步,否则,执行步骤2至7;
(8)运算结束后,根据所得数据计算误差的均值、标准差和变异系数。
采用蒙特卡洛法模拟计算单目机器视觉尺寸测量误差,其整体流程如图3所示。
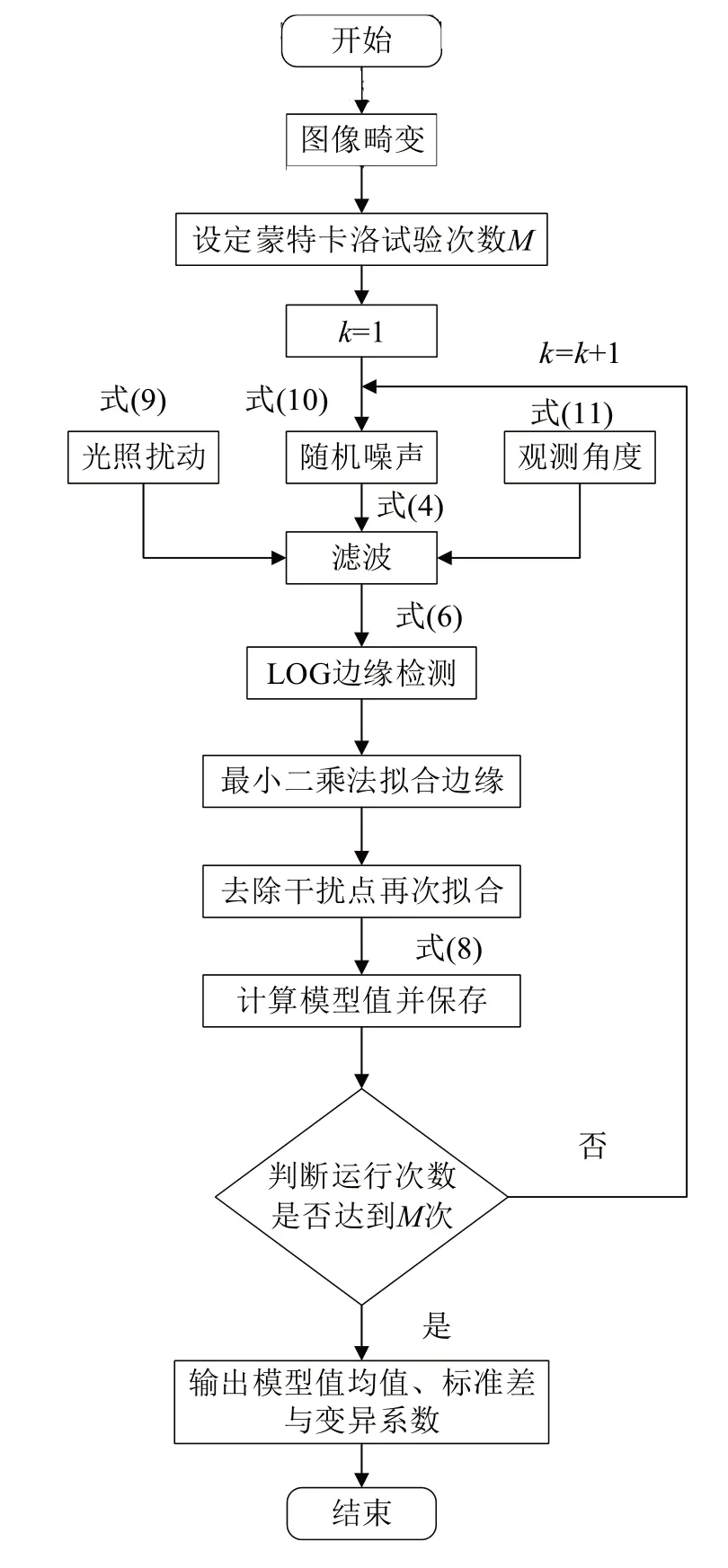
图3 蒙特卡洛模拟流程
4 案例分析
如图4所示,取20.00 mm×34.92 mm的矩形块为检测对象,采用三坐标测量仪检测尺寸。

图4 三坐标测量仪检测过程
采用OSR500-20GM相机并结合实验平台进行实验,相机的分辨率为2 592×1 944,像素深度为8 bit,镜头焦距为16 mm。
为了在理想图像中体现畸变,拍摄标定板的图片并采用Matlab工具箱对相机进行标定。所采用的标定板中每一个正方形的边长都为3 mm,标定板右下角的标记是为了确保拍摄得到的标定板图片原点保持一致。最终选取12张标定板图片进行处理,并且这12张标定板图片的重投影误差都在0.3 pixel以下。处理后得到相机的内参矩阵、外参矩阵和畸变参数。如图5所示,为采用的标定板。

图5 标定板
在不同光照条件和不同观测角度下拍摄390组矩形块照片,采用高斯滤波和LOG边缘检测算子处理图像,两次采用最小二乘法拟合边缘并计算测量误差。390组测量误差数据的均值为20.10 μm,标准差为0.703 2 μm。如图6所示,为测量误差的概率分布。

图6 实验误差分布
在对实验图像处理的过程中,可以得到图像中矩形块长与宽的像素长度,根据标定得到的相机内参、径向畸变参数和切向畸变参数,在理想图像中加入畸变,并加入高斯噪声和泊松噪声,依据图3所示的流程并采用蒙特卡洛法计算出测量误差。
由于外界光照变化、随机噪声以及待测物体与观测台所夹角度变化在实际中较为复杂;因此,这三个不确定性因素的分布形式也是不确定的。根据参考文献和实验角度的调节,简化采用正态分布、泊松分布和均匀分布表示。在蒙特卡洛模拟的图像中加入泊松噪声的值与该像素的灰度值相关。图像中加入的高斯噪声均值为0,方差为0.01。观测角度服从区间(0°,1°)上的均匀分布。泊松分布、高斯分布和均匀分布所选择的参数是最常见的,并且测量结果达到预期要求。参数选取只是作为范例,如果采用其他参数也具有相似的可行性。分布函数的假设值会对误差分析产生影响,目前选取的参数其测量结果较为合理,如果噪声参数过大会导致算法不稳定,过小则无法体现噪声对测量的影响。
蒙特卡洛法的抽样次数M设置为10 000次,抽样得到的平均测量误差为20.32 μm,标准差为3.495 μm。如图7所示,为采用蒙特卡洛法抽样得到的测量误差概率分布图。

图7 数值模拟误差分布
取待测物体与观测台所夹角度为0.5°,当仅考虑高斯噪声时,测量误差均值为20.39 μm,标准差为1.886 μm,变异系数为0.092 50;当仅考虑泊松噪声时,测量误差均值为19.02 μm,标准差为0.414 1 μm,变异系数为0.021 77;当仅考虑待测物体与观测台所夹角度变化时,测量误差均值为14.46 μm,标准差为6.359 μm,变异系数为0.439 8。
5 结论
本文提出了一种单目机器视觉测量误差概率建模与分析方法,该模型能够综合考虑相机畸变和边缘检测算法固定的情况下,外界光照扰动、随机噪声和观测角度变化对测量误差的影响,进而采用蒙特卡洛法模拟计算并结合实验进行验证。
(1)随机噪声对测量结果的均值影响最大,外界光照扰动次之,观测角度的变化对测量结果的均值影响最小。
(2)观测角度的变化引起试验数据的分散性最大,随机噪声次之,外界光照扰动引起测量结果的分散性最小。
(3)外界光照扰动、随机噪声和观测角度的变化在经过一系列图像处理算法运算后,最终所得到的测量误差分布服从偏态分布。针对偏态分布的概率分析问题,将有待于后续的研究。
