原状黄土静止侧压力系数K0特性研究
2023-01-17金娟
金 娟
(陕西铁路工程职业技术学院,陕西 渭南 714000)
0 前 言
静止侧压力系数K0为无侧向变形条件下侧向应力与竖向应力的比值。对于天然土体,K0是岩土工程中一个十分重要的土性参数,随着深基坑工程、地下工程的大量兴建,该参数在岩土工程设计中越来越重要。国内外学者已经开展了大量的室内[1-12]和现场试验[13-15],提出了一些确定K0的理论和经验公式[16-17]。研究结果表面,K0不仅与土的种类[1]有关,即使对于同一种土类,K0还与应力历史[1-4,13]、应力水平[4-7,10-12,18]、结构性[8,11]、固结时间[9]、湿度[10,19]、密度[20]等因素有关。
在已有的计算K0的经验公式中,用土体的有效内摩擦角φ′来估算静止土压力系数,即Jaky公式[16]:
K0=1-sinφ′
(1)
但土的性质对K0有实质性的影响,有效内摩擦角φ′不是确定K0值的唯一土性参数[1]。
因此,本次K0特性研究主要依据K0固结仪量测试样的侧向应力与施加的竖向应力的值来计算分析,静止侧压力系数是K0侧限条件下侧向应力比竖向固结应力的值。计算公式如式(2):
K0=δσh/σv
(2)
1 试验基本情况
1.1 试验土样及制备
试验所用土样均取自西安北郊某工程基坑的原状黄土,属于Q3黄土。试验采用环刀取样,面积30 cm2、高4 cm。为了使试样可以与陶土板紧密接触,以便更准确地量测基质吸力,因此在削样过程中一定要使试样的表面足够平整。为了减小含水量及干密度的差异对原状试样的影响,要控制试样的干密度差值小于0.02 g/cm3,含水量差值小于1%。经测定,其物理特性指标见表1。

表1 原状黄土的物理性质
1.2 试验方法及仪器
为了研究原状黄土的K0特性及含水量与竖向应力对静止侧压力系数K0的影响,对不同含水量原状试样进行K0固结试验,将天然含水率(w0=15.18%)试样增减湿到含水率分别为13.5%、16.55%、21.75%、24.75%、42.47%,试样的含水量皆为通过增湿或减湿的方法把天然含水量的试样改变为不同的含水量。
对于非饱和试样,当试验含水量大于天然含水量时,可采用“水膜转移法”来达到预期的试验含水量,当试验含水量小于天然含水量时,可采用“自然风干法”来控制的试验含水量。试验所用饱和试样均采用抽气饱和法进行饱和,通过此方法饱和的式样,其饱和度可达到95%以上。
为了研究卸荷对K0特性的影响,对16.55%与21.75% 2个含水量原状黄土进行先加荷再卸荷试验。
试验分级施加竖向应力,测量孔隙水压力及竖向变形。施加每级荷载的同时开始记录侧向应力与竖向变形值,待两者均稳定后再施加下一级,直至施加最后一级压力试验结束。对含水量为16.55%及21.75%的2个试样在荷载达到1 600 kPa时进行逐级卸荷,每级卸荷的量与加载相同,回弹稳定标准为竖向变形每小时不超过0.005 mm。
静止侧压力系数K0固结试验所用仪器为GJY型K0固结仪(见图1),对该仪器经过改进后,可以用计算机采集加荷及卸荷过程中试样的竖向变形和孔隙水压力。孔隙水压力即为侧向压力比竖向应力的值为静止侧压力系数K0,表达式为:

图1 K0固结仪
K0=σh/σv
(3)
为了使试验结果更加的准确,在使用K0固结仪进行压缩试验时,操作中应注意的问题详见苏铁志[21]的相关研究。
2 试验结论及分析
2.1 净竖向应力对静止侧压力系数K0的影响
在加载过程中,原状黄土的侧向应力σh与竖向应力σv的关系曲线,如图2所示。
由图2可以看出:不同含水量的原状黄土K0侧限压缩试验的σh-σv关系呈现为先微上凹后微下凹

图2 原状黄土不同含水率σh-σv关系曲线
的曲线,即侧向应力随着竖向应力的增大先缓慢上升,紧接着快速上升(上凹段),紧接着缓慢上升(下凹段)。饱和试样的曲线上凹段与下凹段不明显,近似一条直线。σh-σv关系曲线随着试验含水量的增大而上移,且上凹段与下凹段分界点左移,即分界点的应力随试验含水量的增大而减小,试验含水量越大,分界点越不明显。
由σh-σv关系曲线可以计算出K0侧压力系数,绘制出K0与σv的关系曲线,如图3所示。
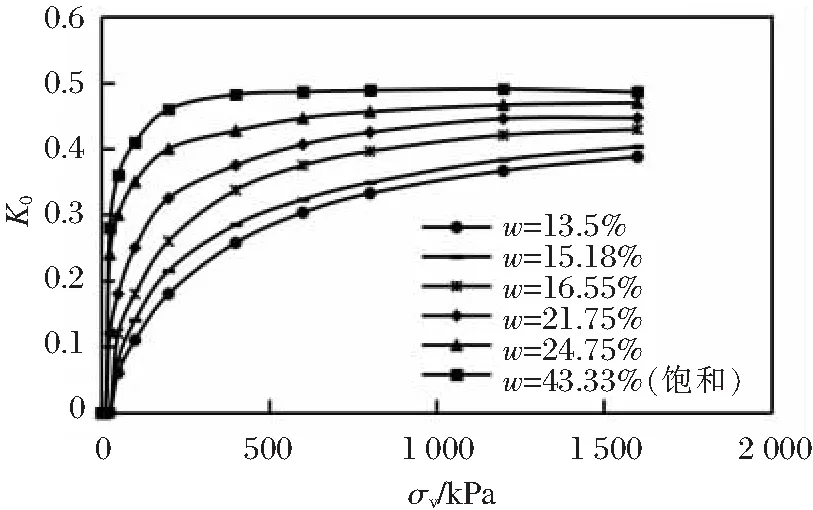
图3 原状黄土不同含水量K0-σv关系曲线
由图3可以看出:原状黄土的K0-σv关系曲线呈现单调上升,分为快速上升和缓慢上升2个阶段,加载刚开始竖向应力较小,K0系数随着竖向应力的增加快速增加,当竖向应力增加到一定值时,K0系数变为缓慢增加且逐渐趋于稳定。含水量对K0-σv曲线影响很大,随着含水量的增大,曲线上移,快速增加段与缓慢增加段的分界点左移,即含水量大的试样分界点所对应的应力小,说明竖向应力对K0有较大的影响。
对试样进行加载的过程中,竖向变形逐渐增大,孔隙比逐渐减小,依据孔隙比与竖向应力的关系,绘制出e-σv关系曲线,如图4所示。
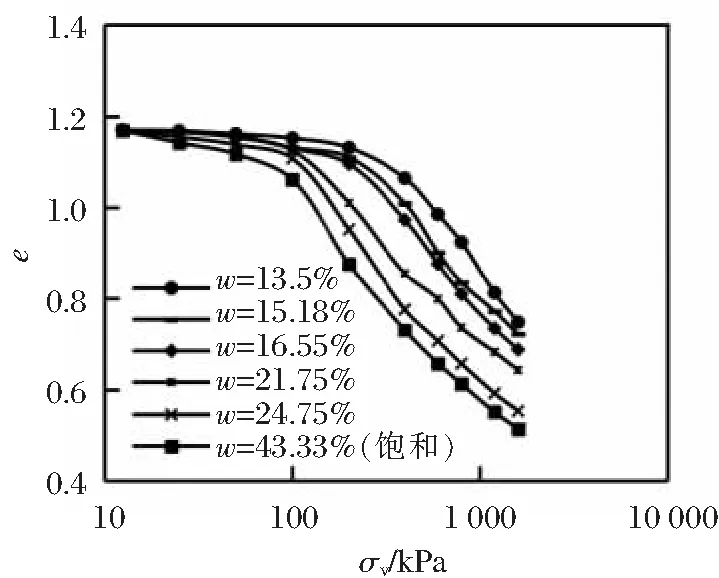
图4 原状黄土不同含水量e-σv关系曲线
由图4可以看出,原状黄土的K0侧限压缩e-σv关系曲线由平缓下降段与快速下降段组成,分界点处所对应的竖向应力为屈服应力Pc,随着含水量的增大曲线下移且屈服应力左移,即试样的含水量越大,其越早达到屈服,在屈服前试样发生弹性变形,随着变形的增大,试样屈服开始发生塑性变形。从e-σv关系曲线得知,试验含水量13.5%、15.18%、16.55%、21.75%、24.75%、43.33%对应的屈服应力分别为400,300,200,150,100,80 kPa。发现屈服应力与K0-σv曲线的转折点的竖向应力值大致一致,说明竖向应力与土样的结构性是影响K0的主要因素,结构性越强对应的K0越小。
由图3与图4可以得到静止侧压力系数K0与孔隙比e的关系曲线,如图5所示。
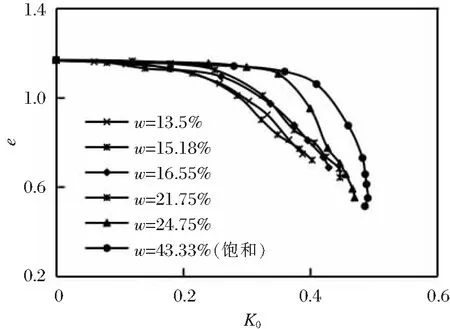
图5 原状黄土不同含水量e-K0关系曲线
由图5可以看出:①原状黄土不同含水量的静止侧压力系数K0随着孔隙比的减小而非线性增大,曲线由快速增加及平缓增加2个阶段组成,且随着试验含水量的增加,曲线快速增加段变短,平缓增加段变长;②当试样含水量较大时,对其加荷载,孔隙比变化不明显时,初期孔隙水压力变化较大,相应地导致静止侧压力系数K0快速增加;随着竖向应力的增大,孔隙比变化较大,在这个较大范围内,孔隙水压力增加相对较小,相应地导致侧压力系数K0缓慢增大;③小含水量对e-K0关系曲线影响不大,曲线分布在一个很小的带中,说明小含水量的原状黄土的结构性强度较大,在承受竖向应力的时候孔隙比与孔隙水压力变化不大。
2.2 加荷条件下含水量对静止侧压力系数K0的影响
通过K0条件下不同试验含水量的原状黄土加载K0-σv关系曲线可以得到不同竖向应力的K0-w的关系曲线,如图6所示。
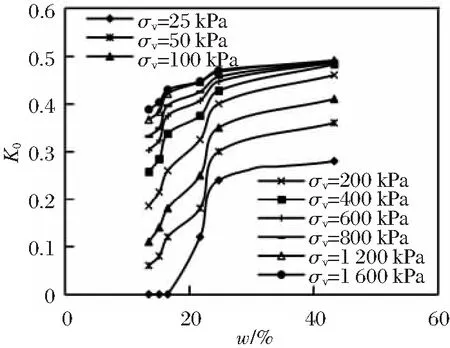
图6 原状黄土不同竖向应力下K0-w关系曲线
由图6可以看出,①原状黄土的K0侧限压缩不同的竖向应力的K0-w曲线均呈现为非线性增加,且曲线随着竖向应力的增大而上移,这是因为含水量相同时,竖向应力越大,对应的孔隙水压力也就越大,相应的K0就越大。这与杨和平等[22]的相关研究的结论相同,即有应力增湿时,相同竖向应力条件下的K0随着增湿的进行而逐渐增大。②随着含水量的增大,K0的增大程度与竖向应力有关,K0-w关系曲线变化规律分为3种情况:第一种,竖向应力较小时,曲线先平缓上升,再快速上升,最后缓慢上升趋于稳定;第二种,随着竖向应力的增大,曲线缓慢增加段逐渐消失,快速增加段变长,最后表现为缓慢上升;第三种,竖向应力很大时,曲线呈现为缓慢上升直至逐渐稳定。这是因为竖向应力较小时,开始土样没有破坏,外荷载由结构强度来承担,K0随着含水量的增大缓慢增大;而当竖向应力逐渐增大时,土样本身强度减弱,增湿与应力的共同作用使土样的结构性逐渐破坏,K0随着含水量的增大快速增大;最后,竖向应力作用达到1 000 kPa以上,土样的结构性已经破坏,增湿与应力的作用对试样来说已不能承受,K0表现为快速增加至稳定。
3 加荷条件下K0系数的数学描述
从图2可知,在不同试验含水量的条件下,原状黄土的无侧限压缩试验的系数不是常数;从图3和图6可以看出其与竖向应力及含水量两者相关。所以Jaky公式中的K0计算公式在这里并不适用,从本试验看出K0系数的表达式需要由竖向应力与含水量共同决定。由陈存礼等[23]的相关研究可知:K0-σv关系曲线近似地可以看成是双曲线的形式,用双曲线来描述的表达式为:
K0=σv/(a+bσv)
(4)
式(4)中a、b为土性参数,为了更好地理解a、b的含义,式(4)可写为:
σv/K0=a+bσv
(5)
将图3中的K0纵坐标变为σv/K0,横坐标不变为σv,因此将图3中的双曲线转变为图7的直线形式,由此可以发现参数a、b的值就是图7所示直线的截距和斜率。由式(5)得知,当竖向应力趋近于0时,a值便为σv/K0;当竖向应力趋近于无穷大时,b值则为1/K0。

图7 原状黄土不同含水量(σv/K0)-σv关系
K0-σv关系曲线初始切线斜率的倒数和K0渐近线的倒数是参数a与b的物理意义,分别用Gi、Koult来表示K0-σv关系曲线的初始切线的斜率的倒数与K0渐近线的值,则a=Gi,b=1/Koult,则式(4)可改为:
K0=σv/(Gi+σv/Koult)
(6)
由图7计算出原状黄土不同试验含水量下的σv/(K0-σv)关系的各直线的截距与斜率值,即为a、b的值,将之与Koutl列于表2中。
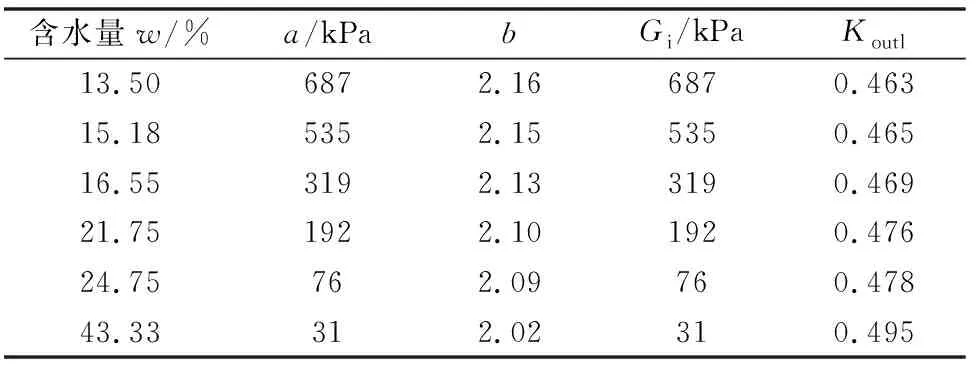
表2 原状黄土不同含水量下的K0系数参数值
从表2中可以看出,原状黄土无侧向变形压缩试验中K0系数表达式的土性参数a与b均随着试验含水量的增加而减小,Koutl随着含水量的增大而增大。Gi、Koutl与含水量w的关系曲线见图8。
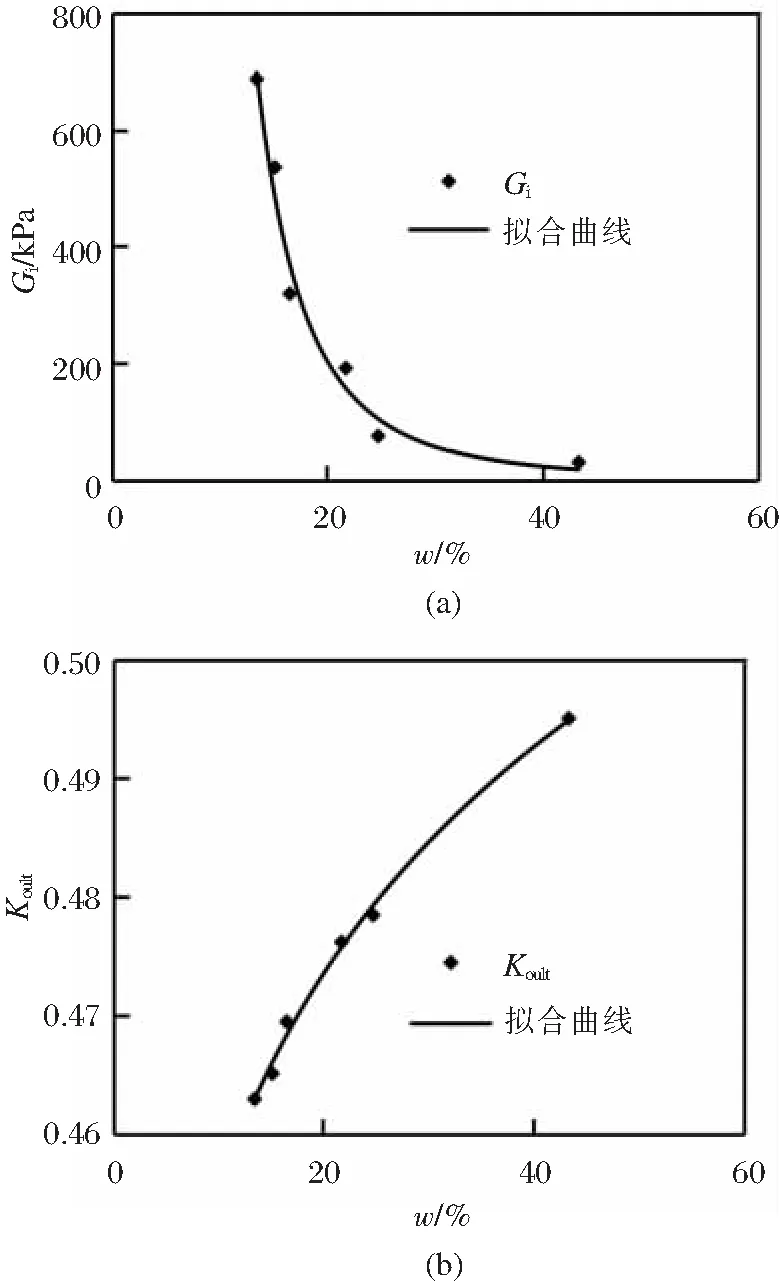
图8 原状黄土含水量w与Gi(a)、Koult(b)关系
从图8可以看出,Gi、Koutl与含水量w的关系曲线均可以用幂函数来描述,其表达式分别为:
Gi=cw-d
(7)
Koult=ewf
(8)
式(7)~(8)中c、d、e、f均为土性参数。基于本次试验所用的原状黄土计算出的c、d、e、f值分别为:1.05,3.26,0.40,0.05。将式(7)与(8)代入式(6),得到原状黄土在无侧向变形压缩试验中,加荷条件下不同试验含水量的原状黄土在不同竖向应力条件下的K0系数值,表达式如下:
K0=σv/(cw-d+σv/ewf)
(9)
由式(9)可以预测:①竖向应力为常数,在无侧向变形压缩试验时,原状试样的增湿K0值;②加荷时,原状黄土任意含水量或竖向应力下的K0系数值。
现用式(9)分别对试验含水量分别为13.5%、15.18%、16.55%、21.75%、24.75%、43.33%的原状试样在加荷条件下进行K0系数的拟合,拟合曲线如图9所示。

图9 原状黄土不同含水量K0-σv关系曲线拟合
从图9可以看出,原状黄土无侧限变形压缩试验中的K0系数通过含水量与竖向应力2个变量进行数值拟合,发现拟合效果较好,即试验数据点与用含水量和竖向应力描述的表达式计算出来的值吻合效果较好。反映了,含水量与竖向应力共同影响原状黄土无侧限变形压缩的静止土压力系数K0,且可以用双曲线来描述。
4 结 论
对不同试验含水量的原状黄土进行了加荷无侧向变形压缩试验,意在通过竖向变形与含水量这2个变量来表示静止侧压力系数。通过试验可以得出以下结论。
(1)同一含水量的原状黄土的无侧向变形压缩中的静止侧压力系数并不是常数,侧向应力与竖向应力的比值并非常数,这对不同含水量也同样适用,这样就不能用我们之前认识的Jaky公式来计算静止侧压力系数。
(2)通过含水量与竖向应力2个变量,对c、d、e、f4个土性参数提出了描述原状黄土的静止侧压力系数的表达式为:K0=σv/(cw-d+σv/ewf)。用这个表达式可以很好地预测:加荷条件下对不同试验含水量的原状黄土施加不同竖向应力,静止侧压力系数K0的值;竖向应力一定时,原状黄土增湿后的K0值。
(3)在加荷条件下,试验含水量相同的情况下,K0系数随着竖向应力的增大而不断增大并逐渐稳定,曲线形式近似于双曲线,大含水量的K0-σv曲线较小含水量的上移,K0系数最大不超过0.5。
