基于模糊神经网络的钻速预测方法

杨 莉, 鹿卓慧, 任伟建, 刘添翼

(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)

0 引 言

准确预测钻井效率(即钻速)是钻井及相关工程中最重要的环节之一[1], 其对评价经济效益、 规划设计地下作业起到至关重要的作用。然而由于钻井过程中存在许多不确定性因素, 使一般模型在钻井工程中很难建立, 又因各个环节存在较为复杂的耦合关系, 从而导致模型预测结果与实际钻速值相差较大。目前研究方式从对单个参数的研究发展为对多目标、 多参数的优化, 并且对参数优化的方法已经从数学模型转为人工智能算法。作为传统机器学习的代表, 支持向量机回归[2-3]在考虑高度非线性的特点时表现出良好的性能, 在实验中对比其他机器学习方法(如k近邻、 线性回归、 多项式回归和决策树)时, 拟合效果更好。然而, 在处理大数据样本时, 由于需要解决二次规划问题, 支持向量机很难实现, 该过程将占用大量的计算时间。随着研究的进展, 目前BP(Back Propagation)神经网络是用于预测钻井速度的主流机器学习算法[4-7], 通过建立影响因素与钻进速度的回归模型得到较高的预测效果, 但其拟合程度需要改进和优化[8-9]。赵颖等[10]提出了极限学习机的方法计算输入层和隐藏层的参数, 不需要调整参数即可完成BP神经网络模型的建立。李琪等[11]利用粒子群优化BP神经网络的权值和阈值, 其预测精度高于BP神经网络等其他模型, 证明了优化后的神经网络在钻井速度预测中具有更高的效率和可靠性。Mohammad等[12]评估了该模型在实际工程应用中的适用性。

目前优化算法研究的重点在于提高钻井效率, 虽然忽视了复杂工况对控制决策和系统稳定性的影响, 但对过于复杂的信息还是需要有经验的工程师解决。为满足各参数之间存在的相互联系和制约的辩证关系, 提出模糊控制模型, 其控制核心模糊规则表可以很好地反映这种客观规律。由于模糊控制和神经网络的互补性, 模糊神经网络已经应用于许多领域的研究[13-15]。笔者将模糊神经网络应用于钻井钻速预测方面, 利用人类思维解决复杂问题, 通过模糊控制和神经网络相结合的方式构建基础优化模型架构。

1 模糊神经网络模型

1.1 模糊控制概述

人脑和计算机有着本质区别, 人脑具有善于处理和判断模糊现象的能力。模糊性普遍存在于人类思维和语言交流中, 是一种不确定性的表现。人类在描述自然现象时, 大脑中会产生一种模糊的概念, 在不断的学习和了解经验后, 会对一般的客观规律进行模糊地划分, 决策出较为理想的结果。通常专家系统建立在专家经验上。模糊控制就是建立在人类思维的基础上, 采取适当策略控制的复杂过程。

1.2 模糊神经网络基本原理

模糊神经网络的每层都对应着Mamdani型模糊控制系统的步骤, 如图1所示。

图1 模糊神经网络模型Fig.1 Fuzzy neural network model

第1层为输入层, 输入向量的每个分量分别对应第1层各自节点, 将输入值x=[x1,x,…,x]输送到下一层。

(1)

其中i=1,2,…,n;j=1,2,…,mi。n为输入量的维度,mi为xi的模糊分割数。

第3层的每个节点分别代表一条模糊规则, 用于匹配模糊规则的前件, 并计算规则的适用度, 即

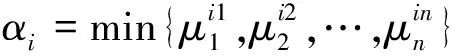
(2)

第4层为清晰化层, 将模糊值转化为清晰值并输出, 即

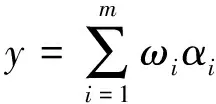
(3)

1.3k均值算法

模糊神经网络要训练的参数有3个, 分别为隶属度函数的中心值、 宽度, 以及最后一层的权重。为获得更好的训练效果, 将输入进行处理, 改进随机初始化或等间距划分隶属度函数的传统方式。通过聚类将相似度高的数据划分为一类, 更好地表示初始语言值变量, 进而使模型获得更好的训练效果, 这种划分也称为硬聚类[16]。采用k-means均值聚类将数据集划分为k个部分, 找到k个聚类点作为隶属度函数的中心值, 同时也作为初始化隶属度函数的参数输入网络中。

给定样本集D=x1,x2,…,xm,k均值(k-means)算法针对聚类所得簇划分C={C1,C2,…,Ck}, 最小化平方误差为

(4)

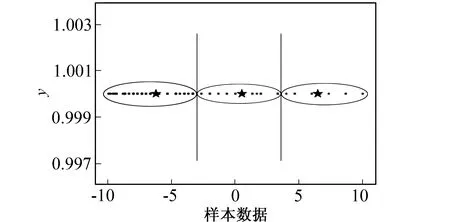
图2 k-means均值聚类Fig.2 k-means clustering

将每个维度的数据进行聚类, 并且每个维度采用5个隶属度函数, 其中首尾两个隶属度函数中心值为取值上下界,k均值聚类结果如图2所示。

图2给出了归一化后数据聚类的结果, 其中3个类别分别用两条直线区分, 星号表示每个类别的聚类中心点, 同时也是模糊语言值的隶属中心点并且分别表示不同的类别, 即模糊语言值。模糊语言值的隶属度函数宽度σi初始化取值为

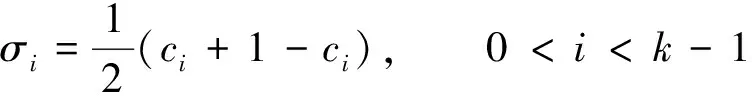
(5)

初始化隶属度函数如图3所示。图3a为聚类后初始化进入神经网络训练的隶属度函数结果, 其中横坐标表示数据在模糊论域的模糊值, 纵坐标表示数据的模糊值所对应的隶属度, 每个隶属度函数表示一个模糊语言值, 如图3a所示可以将全部信息保留, 训练时只需微调神经网络参数即可得到满意效果。图3b为随机初始化高斯函数中心值和宽度后的效果图, 可明显看出随机初始化后会导致很多信息丢失, 这将严重影响模型精确度。

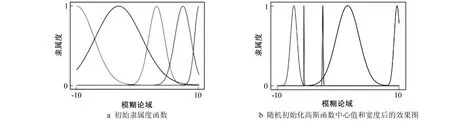
图3 初始化隶属度函数Fig.3 Initializing membership function without restriction

1.4 模型训练

损失函数用于度量预测错误的程度, 由于样本训练集个数有限, 因此选择计算方便的平方损失函数, 即

(6)

其中Y和F(X)是期望输出和实际输出。

平方差损失在计算时放大了预测值与真实值的距离, 因此对误差较大的输出给予较大的惩罚, 有利于误差梯度的计算。利用误差反向传播更新参数, 参数调整的学习算法为

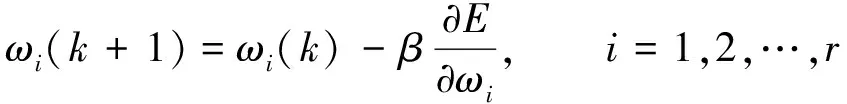
(7)

(8)

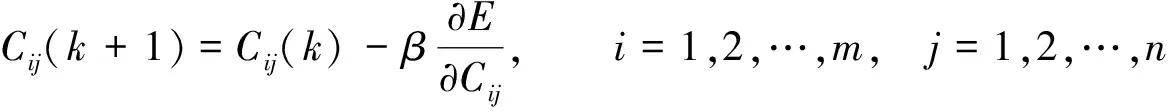
(9)

其中ω是网络最后一层权重, 其物理意义是ωi相当于输出y隶属函数的中心值,Cij和σij分别是隶属度函数的中心值和宽度,β是学习率。

1.5 改进训练流程

训练隶属度函数过程中会出现隶属度中心值和宽度始终增加或减少的情况(见图4), 这是由于训练过程中梯度下降的方向没有改变。

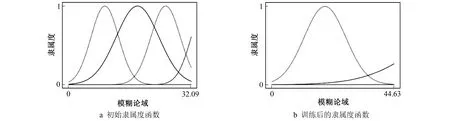
图4 未加限制条件的隶属度函数更新结果Fig.4 Updating result of membership function without restriction

因此要对该网络进行改进, 在每个高斯隶属度函数中加入一个限制区间, 5个隶属度函数的中心值限定范围分别为[-11,-9],[-7,-3],[-2,2],[3,7],[9,11], 即

(10)

其中L、H分别是对应限制区间的上下限。隶属度函数宽度限定范围为[1,4], 即

(11)

规范范围的隶属度函数会最大限度地保留每个语言值的信息, 不会因训练不当造成信息丢失, 训练时超过该限制区间时会保留上一次的值, 以确保模型能清晰地表达每个模糊语言值所代表的含义。

2 实例分析

为验证模型的可行性, 选择某油田钻井数据进行实例分析。经了解, 该油田受断层运动影响, 井底温度高, 可控参数在下井过程中不断的变化。为寻求参数之间的最优组合, 采用Tosun[17]提出的灰色关联分析方法, 选取比较容易获取的6个性能指标钻压、 转速、 排量、 立管压力、 钻进时间以及钻头直径为输入量, 机械钻速为输出量, 通过训练隶属度函数的参数以及最后一层的权重拟合数据。隶属度的数量设置遵循合理性, 过多或过少都会对模型产生不良影响。如果模糊语言值的个数较少, 则会降低对数据的灵敏性, 而个数较多则会增加模型的复杂度。具体讲, 当输入量较大时, 模糊规则的数量将呈指数增长。笔者选取模糊语言值的数量为5个, 以平衡两个方面的影响, 每个输入分为5个部分, 用“小”, “较小”, “中”, “较大”, “大”表示, 构建出模糊神经网络基本模型。

2.1 数据预处理及模型训练

采用某油田钻井数据作为训练样本, 选取对钻速影响较大的6个参数作为训练样本集, 以验证用模糊神经网络建立参数优化模型的可行性。部分测试井训练集样本如表1所示。

获取后的样本需要进行处理, 将实际连续域转换为有限整数离散域, 并将变量按一定比例进行放大和缩小, 以便与相邻模块更好地匹配。

输入物理论域为X=[emin,emax], 模糊论域设置为Y=[-10,10], 则连续论域的一般公式为

(12)

其中emin和emax分别是物理论域的最小值和最大值,x0是当前数据的实际值。物理论域映射到模糊论域的量化因子为

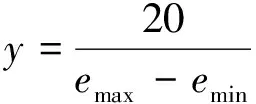
如图5所示, 假设输入的物理论域为[20,560], 则量化因子为1/54, 再计算每个物理论域上的值对应到模糊论域, 作为系统输入。

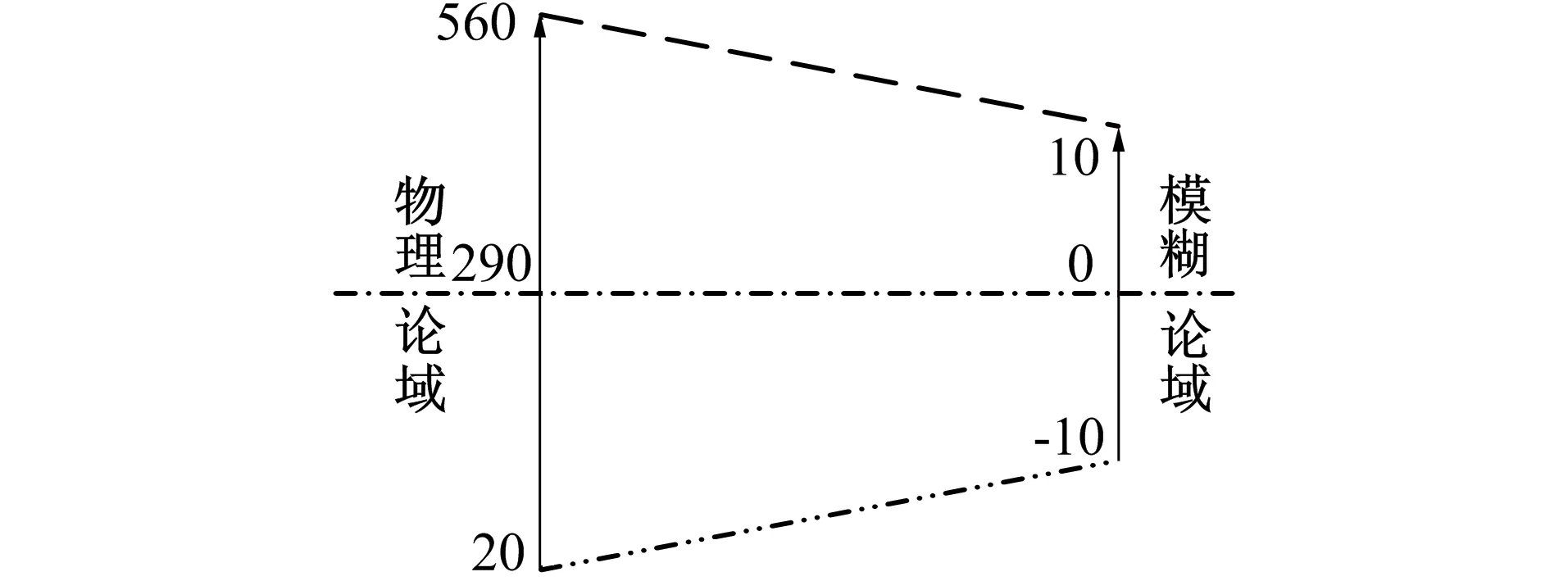
图5 清晰值模糊化示意图Fig.5 Diagram of blurring clear value

2.2 交叉验证

将数据集平均分成10个部分, 其中9个作为训练集, 1个作为测试集。然后将每个训练集依次作为新的测试集, 并将原始测试集放入训练集, 共进行10次交叉实验。取平均绝对误差(MAE: Mean Absolute Error)最小的模型作为最终模型, 根据所有结果对模型进行评价。

该模型是在Anaconda开发环境中使用Python语言构建。实验中, 数据被sklearn库中的model_selection模块划分。通过交叉验证, 评价模糊神经网络对训练数据集的泛化能力。训练模型采用小批量梯度法。初始学习率设置为0.2。在不同优化器的作用下, 对影响模型训练和输出的网络参数进行更新和计算, 以逼近或达到最优值。10次实验的决定系数R2值以及平均绝对误差如表2所示。

表2 模糊神经网络模型在不同优化器作用下的10次实验结果

在不同优化器的作用下不同学习速率下的10次实验得到的平均R2如表3所示。实验结果表明, Adam优化器的大多数精度略高于SGDM(Stochastic Gradient Descent with Momentum)优化器, 因此, 本实验选择Adam优化器用以更新模型。在同区块的数据中, 模型的拟合效果较优, 10次实验结果的R2值均大于0.93且平均绝对误差都控制在0.5以内, 证明了模型训练结果的可行性, 为进一步证明模型的适用性, 还分析了该油气田其他地区的预测结果。

表3 不同优化器作用下不同学习速率的10次实验得到模糊神经网络的平均R2

2.3 结果分析

选择某油田6口测试井在志留系、 石炭系、 泥盆系和奥陶系地层共计144组数据作为测试集数据测试模型的泛化能力, 各地层的预测结果如图6所示。

图6 不同地层预测值与实际值Fig.6 Predicted and actual values of different formations

模型在大部分预测结果中预测值与实际值很接近, 表现出优异的性能, 证明模型对该地区不同区块的预测是可行的。表4给出了某口测试井的模糊规则表。模糊规则表是模糊控制的核心思想。通过训练自动获取的模糊规则表代替依靠经验提取的模糊关系, 从而寻找到参数之间的相互影响对输出量钻速的关系。训练集交叉验证的结果以及测试集的预测结果均说明提取出的模糊规则表具有一定的可信度。

表4 FNN获取的部分模糊规则

模糊神经网络与BP神经网络、 支持向量机在各地层的测试结果如表4所示。模型在多次调参后选择最优参数组合, 其中支持向量机回归采用高斯核函数, 惩罚参数C为1.25, 松弛变量ε为0.05, 停止条件为训练误差小于10-3。设置BP神经网络的层数为3层, 输入层的神经元数为6, 输出层的神经元数为1, 激活函数采用Sigmoid函数。用平均绝对误差MAE与决定系数R2作为模型的评价标准, 可以看到模糊神经网络在大部分地区的效果要优于其他模型, 预测精度有一定的提升。

表5给出了3种模型在不同地层的性能对比, 在评价模型方法上选用平均绝对误差(MAE)以及决定系数(R2)对3种模型进行评价, 结果表明, 模糊神经网络对比其他模型具有一定的优越性。

表5 模型性能对比

图7 误差对比Fig.7 Error comparison

图7比较了3种方法的预测误差, 从图7中可以看出, 模糊神经网络的绝大部分数据预测在3种方法中误差均是最小, 无论从直观还是从精度对比, 模糊神经网络优于其他方法, 证明了模型的优越性。

3 结 论

笔者考虑了在钻井钻进过程中参数之间存在耦合性联系的问题, 建立了模糊神经网络模型。优选了钻压、 转速等6个参数, 通过匹配每个规则总前提的可信度, 进行取小运算得到每条规则的总输出。研究结果表明：

1) 模糊神经网络利用模糊控制的思想处理高耦合问题具有良好的可解释性, 对比不同模型实验的结果可以看到其优势;

2) 在模糊神经网络的模糊层处理过程中, 利用k-means初始化隶属度的中心值, 对模糊神经网络模型进行优化, 方便模型训练;

3) 从仿真结果看, 本方法对该地区施工过程中钻速有较好的预测效果, 模型可以为钻井自动化方面提供技术参考。