非对称半指数势对三角受限势量子阱中极化子性质的影响

白瑞锋，肖景林

（内蒙古民族大学 凝聚态物理研究所，内蒙古 通辽 028043）

0 引言

笔者采用Huybrechts首次提出的关于两次简单幺正变换和线性组合算符这一理论方法，分析非对称半指数势（ASEP）对三角受限势量子阱（TCPQW）中极化子（电子-声子耦合相互作用）性质的影响。将非对称半指数势作为强受限势，三角受限势作为非强受限势，进而研究极化子性质。希望对纳米材料的研究起到重要。在电子与声子相互作用系统的相关科学研究工作中，国内外众多专业研究人员根据多种方法科学研究了低维量子阱中极化子性质。张建芳等［1］研究极化子通过运用由Huybrechts所提出的仅有第二次Lee-Low-Pines简单幺正变换和线性组合算符这一理论方法，并探讨了振动频率和基态能量；MIAO等［2］研究各向异性抛物受限势对RbCl非对称半指数量子阱强电子-声子耦合极化子基态和声子平均数的作用，将其结果归因于量子尺寸限制效应；郑永红等［3］运用两次简单幺正变换并结合线性组合算符方式方法，求出在弱电子-声子耦合极限下，极化子随着x轴方向，y轴方向的受限势的势垒高度、范围和受限强度的变化关联；还有关于这种方式Pekar-type的变分法，SUN等［4］理论上研究了电场对非对称高斯Gaussian受限势RbCl量子阱中单个量子比特的相干时间的影响，结果表明，相干时间随非对称高斯Gaussian受限势量子阱的势垒高度、极化子半径和电场而变化；KHORDAD等［5］结合幺正变换方法，研究温度对非对称高斯量子阱中最低激发态能量、第一激发态能量和束缚极化子寿命的影响，并讨论了和库仑束缚参数和电子-声子耦合强度相关性，讨论强电子-声子耦合极限下的情况可以利用Pekar变分法的方式方法；LIANG等［6］计算了非对称高斯势量子阱中强电子-声子耦合极限下，极化子最低激发态能量和振动频率随温度的变化关系，并且联系有关量子统计相关理论，推导出基态能量和振动频率对温度和电子-声子耦合强度具有一定的依赖性；还有其他变分法［7］，研究了非对称半指数量子阱中浅施主杂质的结合能，研究结构参数导致杂质结合能的显著变化；XIAO等［8］用线性组合算符方式方法，研究了非对称半指数量子阱（ASEPQW）中弱电子与声子耦合极限的相干时间，发现振动频率和激发态能量是势垒高度的增函数，但它们是非对称半指数势（ASEP）范围减函数，相干时间具有全部相反的性质。有关极化子（电子与声子之间的耦合相互作用）在前期科学研究工作中，量子阱生长实验中满足实验要求，z方向受限势受限强度更强［9］。然而，关于强受限的问题却涉及非常少。近年发现2种强受限势：半指数势（SEP）［10］以及高斯势［11］。近年来，笔者从理论上采用相关方法研究了这2种强约束势的性质［12-13］。对于量子阱，z方向有强受限势，x-y方向有非强受限势，如抛物线势。自从HUYBRECHTS［14］首次明确提出一种简单算法，关于采用两次简单幺正变换以及线性组合算符方式方法，在不同电子-声子耦合值下，充分探讨对于光学极化子的不同激发态研究，至此以后，线性组合算符方法就在专业学者们的理论研究中得到了普遍运用，因为它不但可以用于科学研究弱电子-声子耦合极限下极化子［15］的特性，还能够科学研究强电子-声子耦合极限下极化子［16］的特性，更为突出的是，这种方法是目前可以理论计算极化子振动频率［17］的好方法。

笔者采用HUYBRECHTS首次提出的关于两次简单幺正变换和线性组合算符这一理论方法，分析非对称半指数势（ASEP）对三角受限势量子阱（TCPQW）中极化子（电子-声子耦合相互作用）性质的影响。将非对称半指数势作为强受限势，三角受限势作为非强受限势，进而研究极化子性质。希望对纳米材料的研究起到重要作用。

1 理论模型和计算

量子阱中电子被限制在极性晶体中运动，并和体LO声子相互作用。电子-声子耦合极限下，哈密顿量Hamiltonian为［10-12］

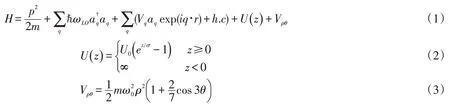
公式中相关物理意义同文献［10］一致，z表示量子阱的生长方向，由性质决定的参数：σ为受势范围，而U0为势垒高度。式（3）中表示三角受限势，其中，ω0是受限强度，ρ是系统的极坐标，θ表示极坐标系统的极角。方程（1）中的Vq和α表示为

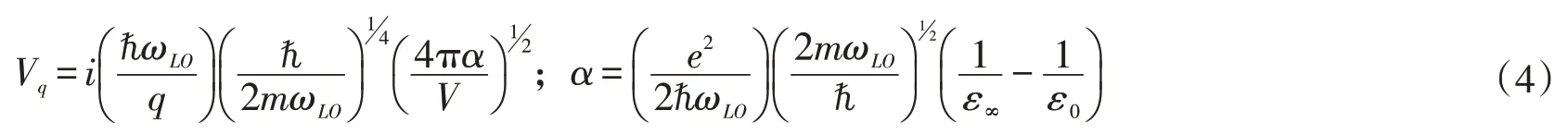
其中，α是耦合常数。V为极性晶体的体积，ωLO为体LO声子频率。对式（1）引进线性组合算符

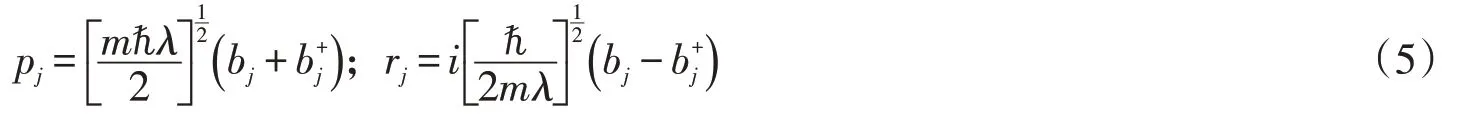
其中，λ表示变分参量，再作幺正变换

确定基态波函数为

经过简单计算，可获得三角势量子阱中弱电子-声子耦合极限极化子基态能量

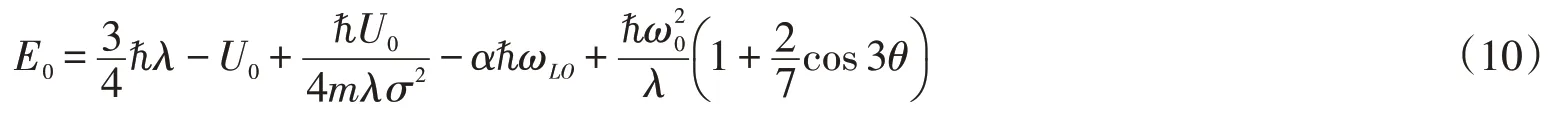
振动频率为

2 数值结果与讨论

理论上探讨弱耦合情况新受限势和极化子基态能量的性质。以半导体晶体材料GaAs为例进行计算，其中，实验参量是 ℏωLO=36.72 meV，m=0.065 7 m0和α=0.068［7］。

三角受限势的受限强度ω0=5.0×1013Hz和极坐标系统的极角θ=0 rad时，基态能量E0随势垒高度U0和受限范围σ的变化关系，见图1。可以清楚地观察到在弱电子-声子耦合极限下，三角受限势量子阱（TCPQW）中极化子的基态能量E0是势垒高度U0的增函数，但是受限范围σ的减函数。导致这一奇特物理现象的原因是，由于势垒高度U0增加，受限势更大，基态能量增加。另一个参数σ的增加将导致一个完全不同的结果，原因是非对称半指数势（ASEP）受限范围σ变大，受限势减小，基态能量降低。

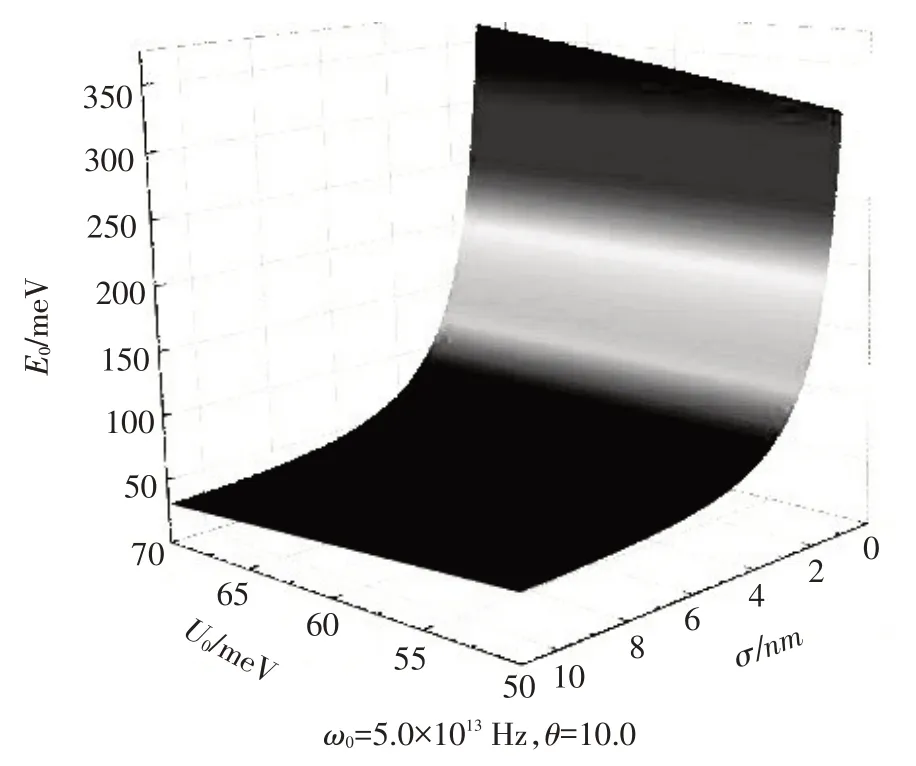
图1 基态能量E0随势垒高度U0和受限范围σ的变化关系Fig.1 The variation of ground state energy E0 with barrier height U0 and confined range σ

当U0=10.0 meV和σ=1.0 nm时，弱电子-声子耦合相互作用极限下三角受限势量子阱（TCPQW）中极化子的基态能量E0随三角受限势（TCP）、受限强度ω0和极坐标系统的极角θ的依赖关系，见图2。可以发现，在弱电子-声子耦合相互作用极限下，三角受限势量子阱（TCPQW）中，极化子（电子与声子相互作用）的基态能量E0伴随着三角受限势（TCP）、受限强度ω0的增加而迅速增加，由此导致这一物理性质规律的因素是，三角受限势（TCP）受限宽度伴随着三角受限势（TCP）受限强度ω0的增加而减小，并且由于粒子运动范围的减小，其基态能量E0快速增加，这归因于奇特的量子尺寸限制效应。还可以看到三角受限势量子阱（TCPQW）中弱电子-声子耦合极限下，极化子的基态能量E0随着三角受限势（TCP）中极坐标系统的极角θ的变化特点，三角受限势的表达式是，它包括2部分内容，一是受限强度ω0部分，另一个部分是极坐标系统的极角θ。受限强度ω0的内容前面已经进行了讨论。而三角受限势（TCP）极坐标系统的极角θ的变化特点由其表达式可以看出，它的示意图形状是三角形状，这也是三角受限势（TCP）的来源，也正因为此称其为三角受限势（triangular constrained potential）。由图2可以看到三角受限势量子阱（TCPQW）中弱电子-声子耦合极限下极化子的基态能量随着三角受限势（TCP）极坐标系统的极角θ发生周期性变化，它还表明极坐标系统的极角θ对基态能量E0的影响随着受限强度ω0的减少变得更弱。原因是随着受限强度ω0的降低，导致三角受限势（TCP）受限长度迅速增加，这导致了随着基态能量的降低，极坐标系统的极角θ的作用效果变弱。

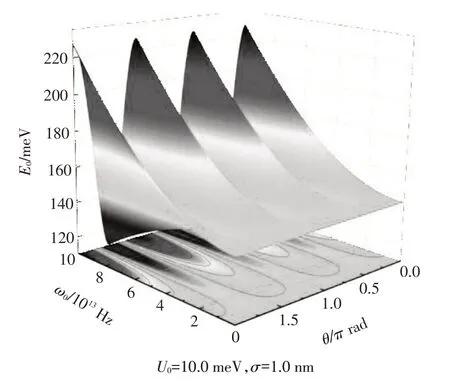
图2 三角受限势量子阱（TCPQW）中弱电子-声子耦合极限极化子的基态能量E0随三角受限势的受限强度ω0和极坐标系统的极角θ的变化关系Fig.2 The ground state energy E0 of the weak electronphonon coupling limit polaron in the triangular constrained potential quantum well（TCPQW）varies with the constrained strength ω0 of the triangular constrained potential and the polar angle θ of the polar coordinate system

3 结论

采用两次简单幺正变换，以及线性组合算符的这一算法的方式方法，深刻研究了极性晶体GaAs半导体晶体材料中极化子的基态能量的特性。弱电子-声子耦合极限下极化子的基态能量随着非对称半指数势（ASEP）的势垒高度U0和半指数势的范围σ以及三角受限势（TCP）的受限强度ω0和极坐标系统的极角θ的变化依赖关系。研究结果表明，弱耦合极化子的基态能量是势垒高度增函数而是受限范围的减函数。基态能量随着受限强度ω0的增加而增大，是极坐标系统的极角θ的周期函数。