类梯形加减速算法在服务机器人中的应用研究

杜正聪，黎安庆 ，李建雄，牟圆圆 ，罗佳源

（西昌学院 a.信息技术学院； b.机械与电气工程学院，四川 西昌 615000）

0 引言

电机在运行过程中，如果速度出现突变，则会产生冲击、震荡等现象。柔性加减速算法可使速度曲线趋于平滑［1-2］。常见的柔性加减速算法有梯形加减速算法、s形加减速算法和指数加减速算法［3-5］。后二者由于参数多，计算量大，在需要快速响应的机器人应用场合不适用。梯形加减速算法存在加速、匀速、减速3个阶段，该算法参数少、运算快，有大量学者对此进行了研究和应用。Chen等［6］提出了一种基于3参数Lame曲线的梯形轨迹优化规划方法，可优化工业机器人的运动轨迹平滑度；吴鹏飞等［7］提出了一种改进型变权重梯形速度优化算法，可减小接触时的碰撞；Yoon等［8］提出一种根据物体固有频率调整梯形加减速参数来减小机构震动的方法；Heo等［9］提出了一种新的梯形速度剖面生成方法，并用位置指令实现了上述算法；Kim等［10］在分拣系统中应用梯形算法使分拣效能提高了40%。但上述梯形算法仅仅在机床、液压等可提前将所有运动规划完的设备中应用。

服务类机器人在异物留存、生物体闯入运动范围、目标运动规律变化等情况时，需中断当前运动规划，但重新进行运动规划时初速度不为零，现有梯形加减速算法不能解决上述问题。本文在梯形加减速算法的基础上提出了类梯形加减速算法，并进行了理论推导。为验证该算法，设计了伺服转台，并编写了伺服控制软件，最后通过实验验证了该算法。

1 梯形加减速算法

梯形加减速算法其速度时间曲线如图1所示。加减速阶段的加速度恒为amax，匀速阶段速度为vmax，t1为加速段结束时刻，t2为匀速段结束时刻，t3为减速段结束时刻，目标位置为Sa。3个阶段运行起止时刻的公式［11-13］如式（1）～（3）所示。

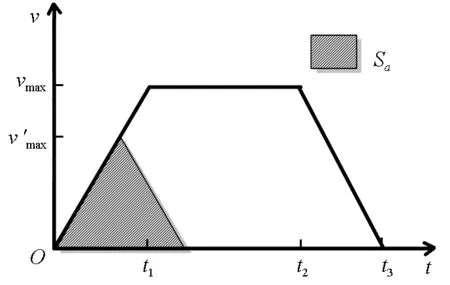
图1 梯形加减速和三角形加减速运动图

若Sa减小，首先应缩短匀速段运行时间，直至为零；若Sa进一步减小，则应同时缩短加、减速阶段运行时间。此时加速段尚未结束，运动直接进入减速段，原来3阶段的梯形加减速变为2阶段的“三角形”加减速运动。判定该情况是否出现的条件如式（4）所示，运动规划如式（5）～（7）所示。

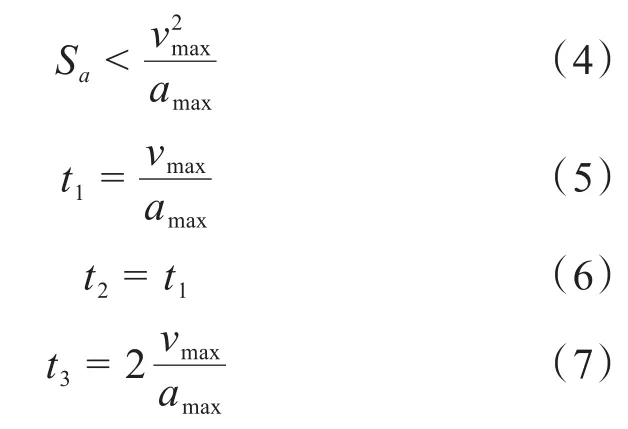
以上是初末速度均为零的梯形加减速算法，该算法适用于机床、液压设备、绘图仪等无须中断运动规划的设备［14-15］。

2 类梯形加减速算法

对于服务类机器人，当运动出现中断时，假设位置为S0，速度为V0，其余参数amax、vmax、t1、t2、t3的含义均与上文的一致，新的目标位置为Sb。设S′b=Sb-S0为下一步运动规划需要运动距离，对S′b不同，有不同运动策略。

当S′b满足条件时，运动规划为加速、匀速、减速3段，各段的起始时刻分别如式（8）～（10）所示，其运动曲线如图2a所示。

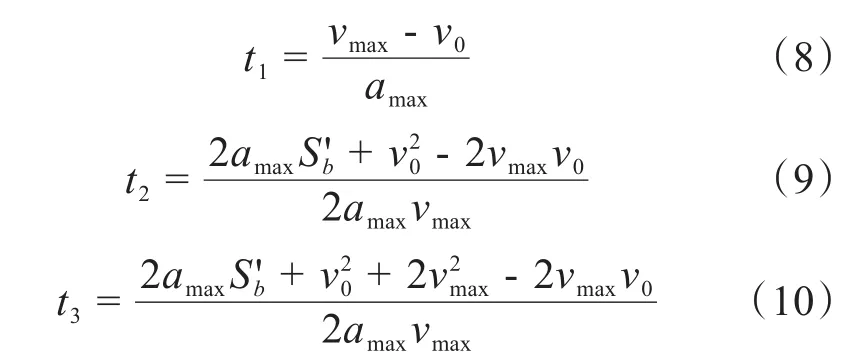
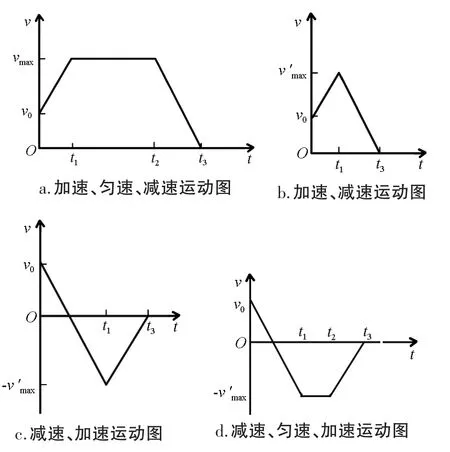
图2 类梯形加减速算法速度-时间曲线图

当S′b减小时，缩减匀速段时间。当S′b满足条件时，匀速段运行时间缩减为0，S′b再减小则应缩减加、减速段运行的时间，最大速度为v'max（v'max＜vmax）。加、减速段的截止时刻表示如式（11）～（13）所示，其运动曲线如图2b所示。

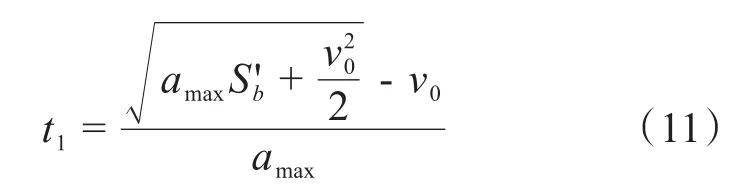
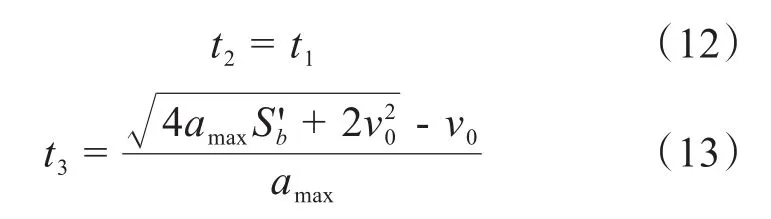
S'b继续减小，当满足条件-S2=时，运动规划为开始就匀减速，速度减为零后反向加速运动，速度达到-v'max（-v'max＜-vmax），再匀减速至停止。减、加速段的时刻计算分别如式（14）～（16）所示，其运动曲线如图2c所示。

S'b进一步减小，当满足条件时。开始即匀减速，速度减为零后反向加速运动，直到反向运动速度达到-vmax，并保持匀速运动后才匀减速至停止。减速、匀速、加速段的时刻计算分别如式（17）～（19）所示，其运动曲线如图2d所示。

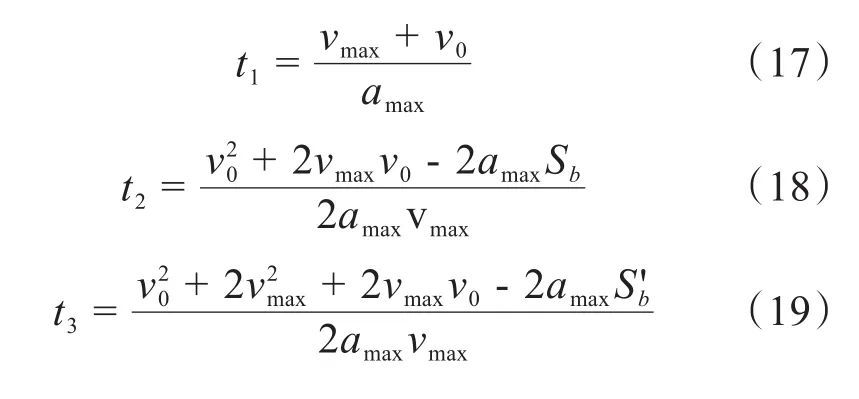
3 伺服试验台硬件设计

为验证上述算法，本文设计了伺服试验台。该试验台如图3所示，主体框架呈立方体结构，使用20 mm规格方钢管切割焊接，其余部件安装在框架上。框架顶部安装回转轴承以及承台，在承台上可固定用于目视粗略直接测量角度的360°标记板；框架左侧安装一根指示转台位置的指示杆。承台与电机之间使用同步轮系传动，同步轮系减速比为5∶1，由17齿小轮85齿大轮及同步带组成。

图3 伺服转台结构图

控制电路（图4）由STM32F103单片机作为运算控制模块，该单片机可提供32位、72 Mhz的算力。经验证，在3闭环结构下该模块可实现500 Hz以上的控制频率，满足本设计要求。驱动单元主芯片为BTN7971，最大提供45 V、50 A负载，具备电流测量功能。根据电机参数，将其工作电压设置为24 V，最大通过5 A电流。电机选用80∶1减速比的直流行星减速电机，该电机尾部装配了AS5048磁编码器作为位置反馈传感器，其分辨率达到0.02°。整机供电使用开关电源模块，将220 V转换为24 V。DC-DC转换器将24 V转换为5 V后提为控制系统供电。系统运行时，单片机通过驱动单元驱动电机运行，电机角度通过磁编码器反馈到单片机当中形成闭环控制。电机运动通过行星减速器和同步轮系传递到承台上。在调试时，电机还可通过串口与上位机通信，显示速度、位置等信息。

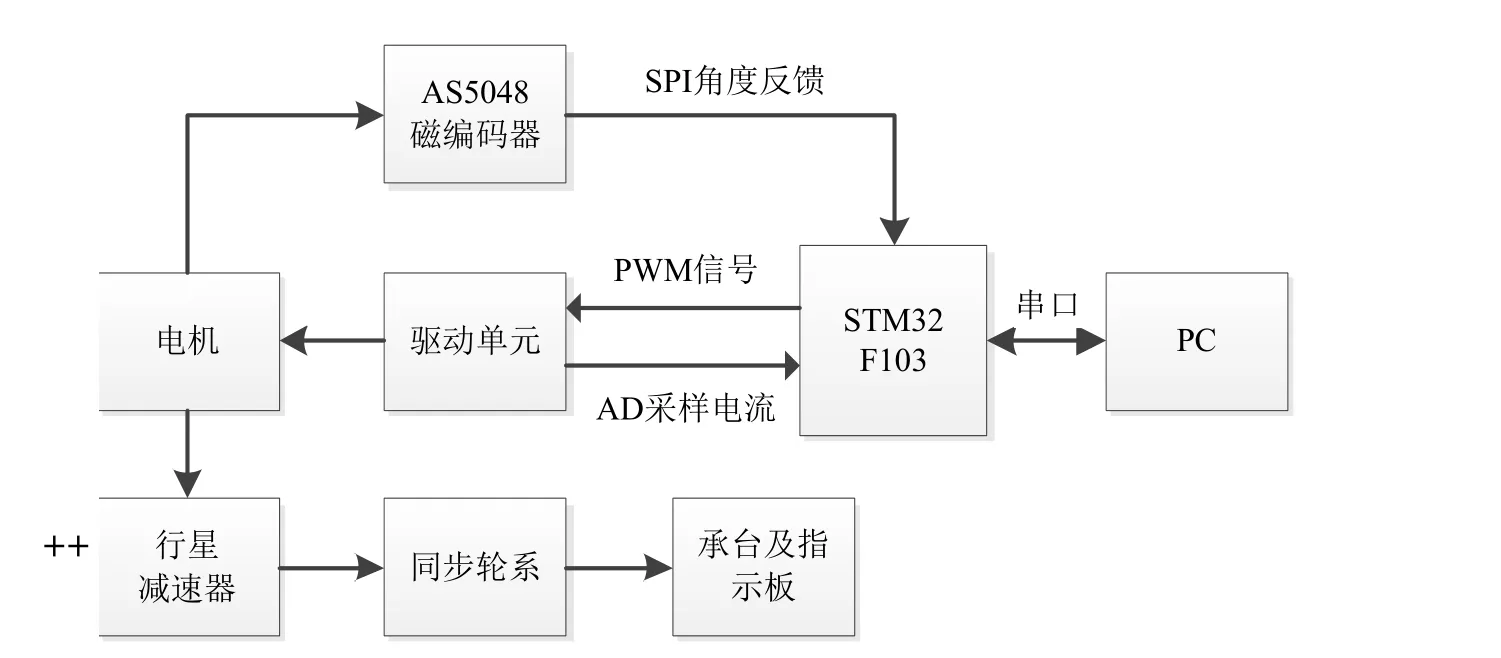
图4 控制系统结构框图

4 伺服试验台软件设计

本文针对硬件平台进行了软件设计，选择在MDK上使用C语言开发程序。程序流程图如图5所示，程序起始后首先接收运动参数：Sb、S0、v0、amax、vmax。计算得出各段运动的起止时刻，之后进入运动控制循环。循环第1步根据当前运行时间计算下一步运行的位置Snext，将该位置指令送入伺服程序运算得到PWM信号，最后经驱动单元放大功率，驱动电机。如果运动控制循环运行过程中出现运动中断指令，则程序记录当前位置为S0、速度为v0，并根据上述数据重新进行运动规划。

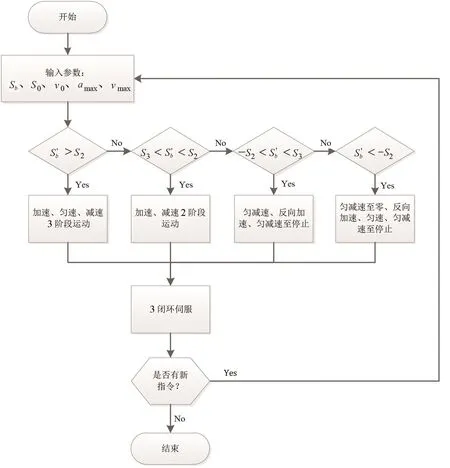
图5 运动规划及伺服环路软件流程

5 实验与验证

在每次伺服环路运行过程中，程序将当前测试数据通过串口发送给PC机。PC机对接收到的数据进行处理并显示。

首先验证运动规划的作用。设置初始位置为0（°），当给定位置指令S= 3×106（°）后，伺服转台在没有运动规划的情况下，以机电系统提供的最大加速度向目标运动，并且在目标点附近停止。电机运行速度在0和3.5 s时均出现阶跃性突变，在3.5 s时甚至出现较大过冲，产生机械冲击（图6）。

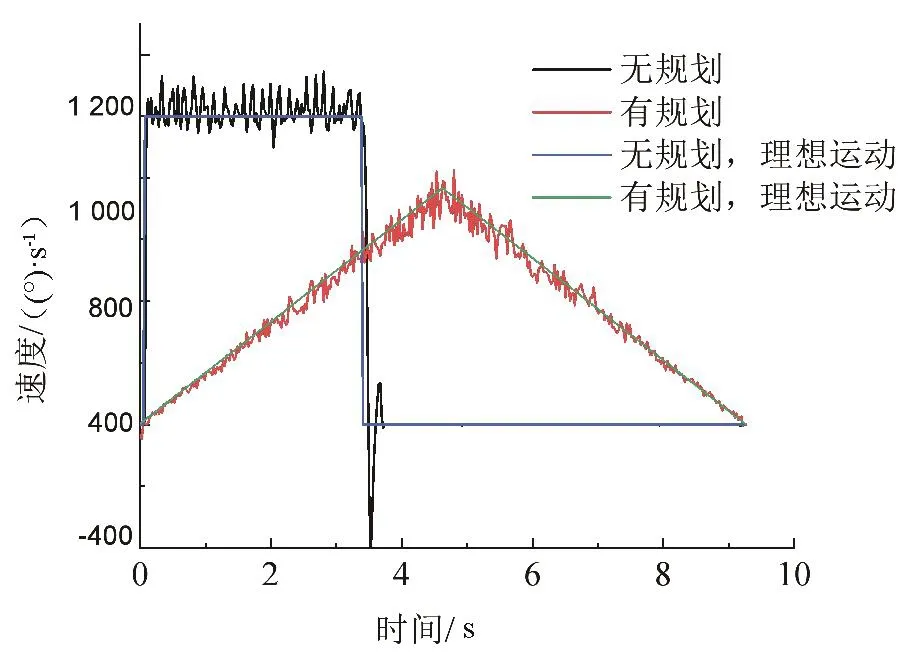
图6 有无使用运动规划的速度测试曲线

同样的测试条件，在使用梯形加减速算法情况下，速度指令以及速度响应均缓慢变化，加速度相比较之前小，机械冲击更小。

为验证不同目标位置下算法能否满足设计要求，设定目标位置值逐步减小。具体值根据上述类梯形加减速算法的4种位置而设置：S1= 1×107（°），S2=3×106（°），S3= -3×106（°），S2= -8×106（°）。设置初始位置为0 （°），初始速度为400 （°）/s。

伺服转台的测试曲线及理想曲线如图7所示。所有曲线均从400起始，表明算法具备非零初速度规划能力。所有曲线的速度均未出现突变，加速度没有出现陡增现象。由于目标位置为正，S1、S2的曲线全部都在正向，而S3、S4由于目标位置为负，曲线的大部分为反向速度。S2、S3曲线由于运动目标位置距离初始位置较近，所以没有出现匀速段运动。

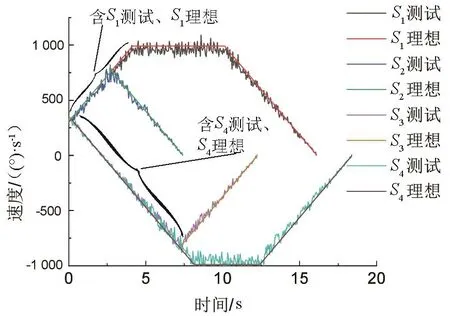
图7 不同运动目标的速度测试曲线

为验证类梯形算法在上一次运动规划未完成，有残余末速度的情况下，多次重新规划目标的能力，设计了4段运动。后3段运动均在上一段运动未执行完毕的情况下，重新做运动规划。表1记录了每次运动规划的目标位置，以及重规划时的运动状态。该实验的理想曲线和实测曲线如图8所示。曲线中S2、S3、S4处分别进行了速度重规划，3处初速度均不为零，但理想速度和实测速度曲线均连续，表明算法实现了任意运动阶段中断现有运动规划，且重规划运动时运动速度没有突变。

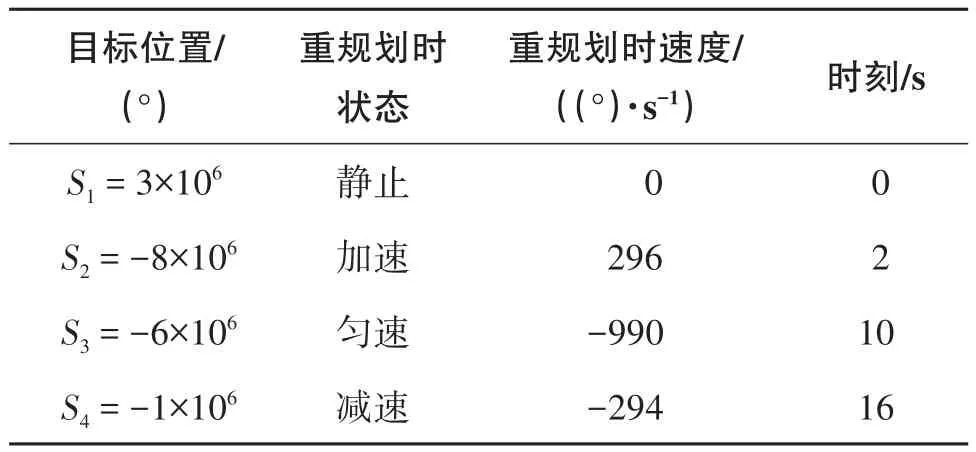
表1 多次重规划运动的目标位置及状态

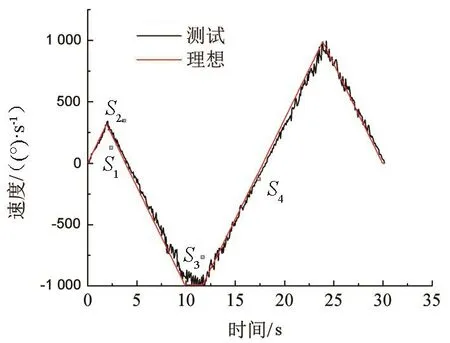
图8 中断运动规划后重规划运动图

6 结论

本文针对服务类机器人运动规划需要被中断的实际要求，在梯形加减速算法的基础上提出了类梯形算法。并从机械、电气、控制方面进行设计，搭建了伺服转台。通过实验表明，该算法可根据目标点位置不同而采取最佳运动策略，达到速度不突变的要求。该算法可以根据当前运动状态和目标位置随时重规划运动，以满足服务机器人运动规划中初速度不为零的要求。