基于超声传感和高斯过程回归的锂离子电池SOC估计研究

牛 牧, 陈则王, 张淞源, 王友仁

(南京航空航天大学 自动化学院, 江苏 南京 211106)

0 引 言

锂离子电池荷电状态(State of Charge,SOC)是描述电池运行状态的重要参数,其通常表示为电池剩余电量与容量的比值[1-2], 电池满充时SOC为100%, 电池满放时SOC为0。 国内外文献给出了多种SOC估计方法[3-4],可分为计算法和估计法两类,计算法直接由定义公式计算获得SOC,估计法通过构建电池监测信号与SOC之间的关系模型来估计SOC[5]。根据关系模型构建的具体方法,估计法又可分为参数估计法和拟合法。

锂离子电池SOC估计方法中, 计算法需要确定SOC初始值及精确测量电流值; 参数估计法能够实时跟踪电池电压和电流的变化以更新SOC估计值, 但其实现过程相对复杂、 计算要求高; 拟合法简单易行, 但需要离线训练数据。 现有方法应用于SOC在线估计时均存在一定不足, 难以在线、 精确估计复杂动态工况下的电池SOC。

近年来,Ladpli等[6-7]研究了充放电周期内超声信号随SOC及电池健康度(SOH)的变化趋势。Gold等[8]和Chang等[9]分析了超声特征和SOC之间的关系, 并构建了超声特征与SOC的线性模型。Davies等[10]基于支持向量回归模型及超声特征实现了恒流充放电状态下电池SOC和SOH 估计。 邓哲等[11]总结概述了现有超声检测技术在电池表征领域的应用, 包括内部气体检测、 电解液浸润测试、 电池析锂检测、 电池荷电状态测量、 电池寿命预测等, 对其发展前景进行了展望。 周世杰等[12]基于超声测量和神经网络提出了一种动力电池SOC估算方法。 基于超声传感的技术研究为锂离子电池状态评估开辟了一条新思路[13-15], 但目前仍处于初步探索阶段。

本文针对现有超声SOC 估计中存在样本量小、 实验工况单一、 模型建立不完善等问题, 提出了一种基于交叉验证高斯过程回归的锂电池SOC估计方法; 为探究在复杂工况下该方法的有效性,在已有蓄电池充放电实验平台的基础上, 增加超声模块, 选用《USABC电动汽车电池试验手册》中的动态应力测试工况(Dynamic Stress Test,DST)以及自定义动态工况(Custom Dynamic Test,CDT)CDT1,CDT2对锂离子电池分别进行3种温度(25℃,35℃,45℃)下的动态工况试验。 图1为3种工况的电流-时间曲线图。 考虑采样数据有限的问题, 采用交叉验证法, 基于对锂离子电池进行超声检测得到的透射波数据(幅值与飞行时间), 建立高斯过程回归模型, 并考虑温度因素, 探究不同条件下该模型进行SOC估计的有效性。

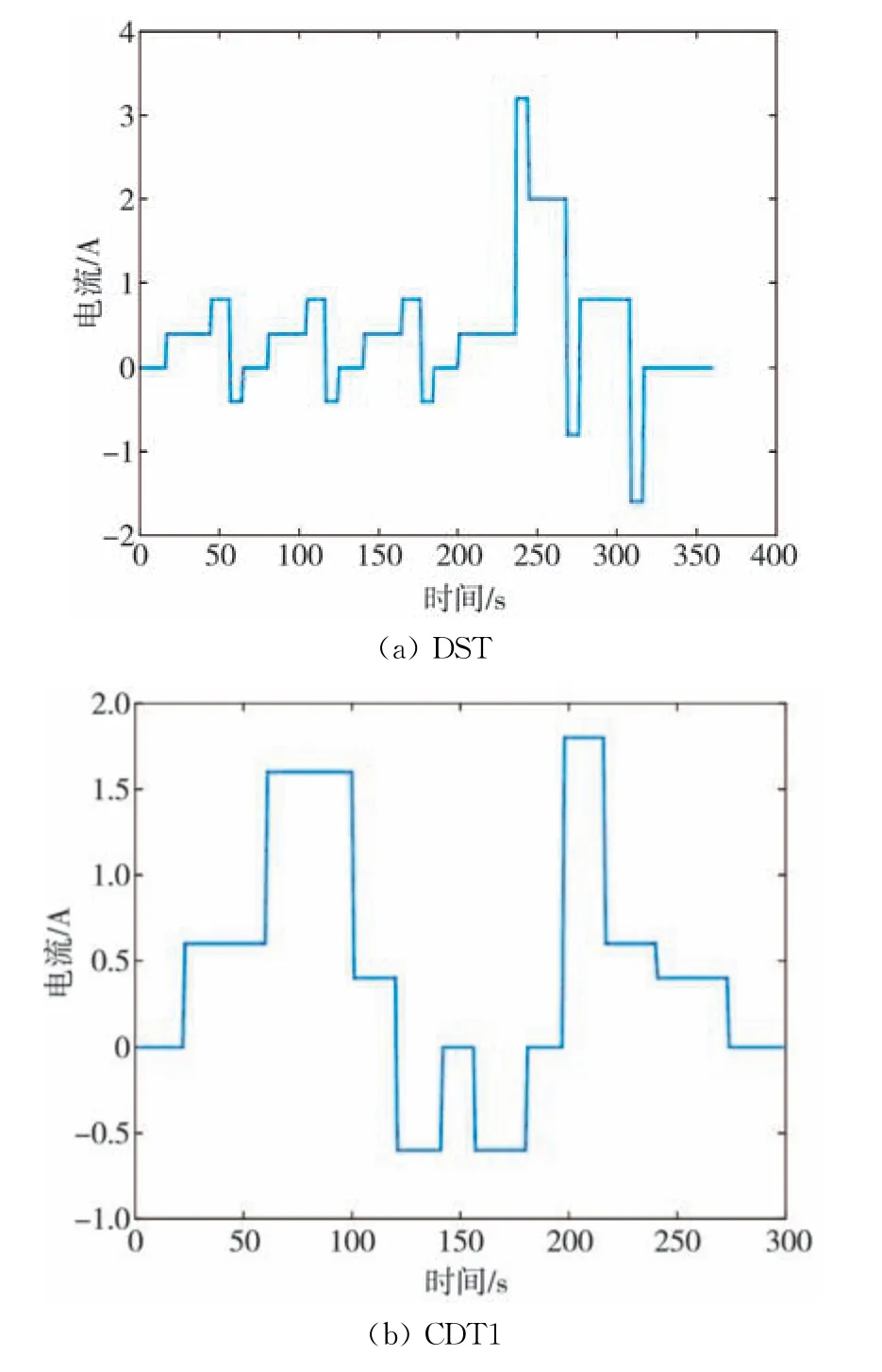
图1 动态工况测试电流-时间曲线Fig.1 Test current-time curve under dynamic conditions

1 超声检测的基本原理与模型建立

1.1 锂离子电池状态变化对超声信号影响的理论分析

超声检测技术作为常用无损检测方法, 始于1930年, 其具有检测对象范围广、 缺陷定位准确、灵敏度高、 便于现场使用等特点, 已广泛应用于结构健康监测和材料内部缺陷检测中。 超声波的本质是一种声波, 当在压电材料上(换能器)施加电压时, 压电材料将发生伸缩振动, 将这种振动施加到锂离子电池上, 电池表面也会产生振动,从而产生超声波, 通过接收与电池内部材料层作用后的超声信号测定其特征信息, 从而获取材料中弹性模量、 硬度、 厚度等物理参数的变化。

锂离子电池状态变化的本质是电池内部材料及结构的变化, 这会导致正负极材料的密度和模量发生变化, 根据Newton-Laplace方程, 超声波在电池每个电极层的传播速度和阻抗取决于材料模量及密度, 而超声传播速度和超声阻抗又反映为超声飞行时间(TOF)和超声信号幅值(PA)等特征的变化, 也就是说, 锂电池状态的改变会引起材料模量和密度的改变, 进而造成超声TOF 和PA的变化, 因此, 可以通过观测TOF和PA 的变化建立模型来估计电池状态的变化。

1.2 高斯过程回归

常用的数据驱动方法包括神经网络、 支持向量机及高斯过程回归(GPR)等。GPR是一种基于统计学理论发展而来的学习机, 其以概率分布来表示函数输出的先验知识, 并在泛函空间建立模型, 基于数据间的相关性构造协方差函数, 通过推理进行计算。 它对处理高维数、 非线性的分类、回归问题具有很好的适应性, 较传统非线性建模技术而言, 具有可调整参数少、 可解释性强等优点。 鉴于此, 本文采用GPR构建锂离子电池SOC估计模型进行电池SOC估计。

如果一个函数符合高斯过程(GP)分布, 那么它的性质就完全取决于均值函数和协方差函数, 即

式中: 预测均值向量ˉf*即为GPR 模型的输出,也即f*的预测值。

在GPR 模型定义的泛函空间中, 协方差函数在GPR 模型中起到关键作用, 它表达了一种相似性或接近性, 对所要学习的函数提供了假设信息。常见的协方差函数包括: 平方指数协方差函数(Squared Exponential,SE), 有理二次协方差函数(Rational Quadeatic,RQ),Matern协方差函数等。

1.3 交叉验证回归模型

交叉验证(Cross Validation,CV)是在机器学习建立模型和验证模型参数时常用的办法, 一般用于评估一个机器学习模型的表现。 交叉验证的基本思想是在某种意义下将原始数据进行分组,一部分做为训练集, 另一部分做为验证集, 首先用训练集对分类器进行训练, 再利用验证集来测试训练得到的模型, 以此来做为评价分类器的性能指标。

交叉验证回归模型(Regression Partitioned Model)是一组在交叉验证折叠上训练的回归模型, 通过使用一个或多个K 折方法交叉验证估计回归的质量。

2 锂电池超声传感平台的搭建和实验

2.1 实验平台

在实验室已有蓄电池充放电实验平台的基础上(见图2), 采取透射模式(见图3), 增加超声模块(见图4), 完成锂离子电池超声实验平台的搭建。

例如，于干燥、低温或者风沙较大的环境下，没牛羊患疥癣类寄生虫病的可能性会大幅度提升，这时由于此类气候环境有利于疥癣病原体的生长和传播，牛羊在感染此类寄生虫以后，会出现全身奇痒、皮肤变厚且逐渐粗糙化、机体消瘦及脱毛情况严重等症状。同时，此类寄生虫会长时间的存在于牛羊的体外表层，吸取牛羊机体的营养，致使患病机体日益虚弱化，最终因免疫力极具降低而死亡。想要提升牛羊寄生虫病的预防及控制质量，我们需要注重对影响各种牛羊寄生虫的生长及繁殖条件的因素及其与寄主间存在的关系加以充分的了解和分析，同时，也需要对寄生虫的生长及传播条件等进行有效掌握和科学控制。

图2 蓄电池实验测试平台实物图Fig.2 Physical image of the battery experimental test platform

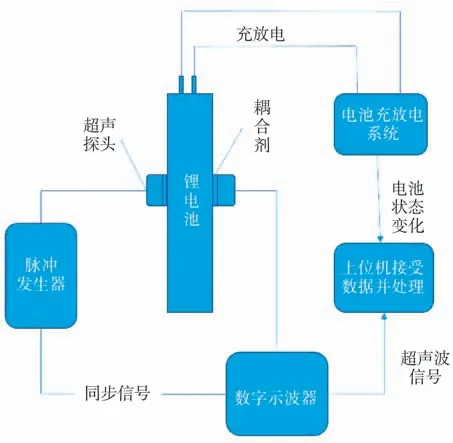
图3 透射模式超声实验图Fig.3 Transmission mode ultrasound experiment diagram

图4 超声实验平台Fig.4 Ultrasound experimental platform

在锂离子电池进行不同工况下的充放电时,对其进行超声测量, 并对得到的数据进行记录,包括温度、 电池实时电流电压以及得到的超声透射波的幅值与飞行时间。

2.2 实验条件与数据分析

以钴酸锂袋装电池(1.5 Ah额定容量)为研究对象, 对锂电池在3 种温度下(25℃,35℃,45℃)进行3种工况(DST,CDT1,CDT2)的充放电实验, 并对电池进行超声信号测量, 得到的数据如图5、 图6所示。 图7为采用安时积分法得到的不同工况下电池SOC变化曲线。

图5 不同工况下超声幅值变化曲线Fig.5 Variation curve of ultrasonic amplitude under different working conditions

图6 不同工况下超声飞行时间变化曲线Fig.6 Variation curve of ultrasonic transit time under different working conditions

将图5～图7对比可以看出, 超声信号幅值和飞行时间与电池SOC的变化基本呈线性相关,幅值与SOC呈线性负相关, 飞行时间与SOC呈线性正相关。 且相比于幅值, 飞行时间的变化呈现出明显的分层, 相同温度下的TOF具有相似的上升趋势, 不同温度下的TOF则有明显的差异,表明TOF展现出与温度因素极高的相关性, 幅值则没有观察到这种特性。

图7 不同工况下电池SOC变化Fig.7 Battery SOC changes under different working conditions

3 试验结果分析

3.1 单一温度下,SOC估计结果分析

以25℃环境温度为例, 分别选取不同的协方差函数、 输入参数、 折叠次数, 构建不同的交叉验证高斯过程回归模型(RPGPR)对锂离子电池SOC进行估计, 并对比分析SOC估计结果。

(1) 协方差函数对SOC估计结果影响分析

以DST,CDT1,CDT2 3种工况下的数据作为测试训练数据集, 选取幅值作为输入, 构建PRPGPR模型, 分别选取不同的协方差函数(SE、RQ、Matern32协方差函数)进行SOC估计, 折叠次数默认为10次。

图8为基于不同协方差函数的锂电池SOC估计曲线, 表1给出了SOC估计性能评价指标, 由图表分析可知, 当采用SE函数时,SOC估计的均方误差(RMSE)最小, 得到的预测曲线较贴合原始曲线, 所以, 在后续实验分析中选定SE为协方差函数。

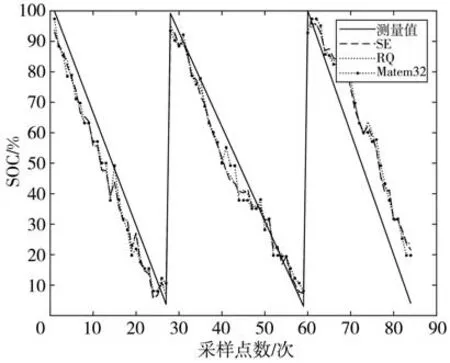
图8 不同协方差函数下锂离子电池SOC估计结果Fig.8 SOC estimation results of lithium-ion batteries under different covariance functions

表1 不同协方差函数下锂离子电池SOC估计性能评价指标Tab.1 Under different covariance functions,lithium-ion battery SOC estimation performance evaluation index evaluation index

(2) 输入参数对SOC估计结果影响分析

图9为基于3种模型的锂电池SOC估计曲线, 由图可知, 采用PA-TOF作为模型的输入参数时, 得到的预测曲线相比于只采用PA 或只采用TOF时得到的预测曲线更加符合原始数据变化曲线。 同时由表2可以看出, 采用TOF-PA 作为输入参数进行的SOC估计误差最小,RMSE仅为3.27%, 估计性能最优, 因此, 选定TOF-PA作为输入参数进行后续SOC估计。

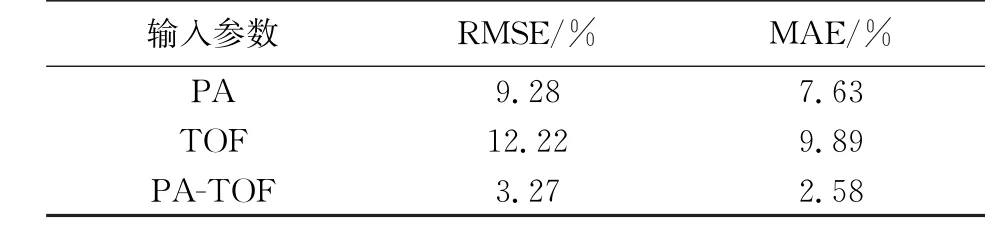
表2 不同输入参数下锂离子电池SOC估计性能评价指标Tab.2 Under different input parameters,lithium-ion battery SOC estimation performance evaluation index

图9 不同输入参数下锂离子电池SOC估计结果Fig.9 SOC estimation results of lithium-ion batteries under different input parameters

(3) 折叠次数对SOC估计结果影响分析

以DST,CDT1,CDT2 3种工况下的数据作为测试训练数据集, 分别选取折叠次数为5,10,15,20, 构建PT-RPGPR 模型, 进行SOC估计。图10为基于4种不同折叠次数的SOC估计结果,4种折叠次数对应的SOC估计性能评价指标如表3所示。 由表3可知, 当折叠次数≥10次之后,估计误差的变化幅度很小, 考虑到计算时间及运行内存,在后续实验中都选择折叠次数为10次。

图10不同折叠次数下锂离子电池SOC估计结果Fig.10 SOC estimation results of lithium-ion batteries under different folding times

表3 不同折叠次数下, 锂离子电池SOC估计性能评价指标Tab.3 SOC estimation performance evaluation index of lithium-ion battery under different folding times

3.2 不同温度下,SOC估计结果分析

上节实验在25℃环境温度下, 分析了RPGPR模型各种设计方法对SOC估计性能的影响。但在锂电池的实际应用工作环境中, 环境温度可能会有很大差异, 为了验证该方法在不同环境温度下的适用性, 本节对不同环境温度下的SOC估计模型性能进行进一步验证和评估。

基于3种不同的温度(25℃,35℃,45℃),在原有输入参数中加入温度参数, 构建T-PTRPGPR模型进行SOC估计。 图11为3种不同温度下, 增加温度参数的T-PT-RPGPR模型与PTRPGPR 模型分别进行SOC 估计的对比曲线,图12绘制了3种温度条件下, 基于两种RPGPR模型进行SOC估计的MAE对比图, 表4给出了更为详细的基于不同RPGPR 模型的锂离子电池SOC估计性能评价指标。

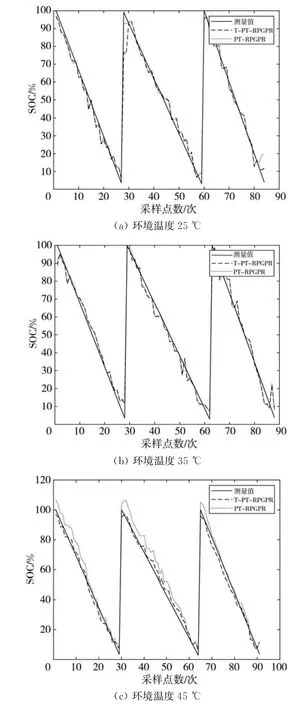
图11 不同环境温度下的不同模型SOC估计曲线Fig.11 SOC estimation curves of different models under different ambient temperatures

图12 3种温度条件下, 基于两种RPGPR模型进行SOC估计MAE结果Fig.12 SOC estimation MAE results based on two RPGPR models under three temperature conditions

表4 不同环境温度下, 是否加入温度参数对SOC估计性能评价指标Tab.4 At different ambient temperatures,whether to add temperature parameters to evaluate the performance evaluation index of SOC

综合分析可知, 采用交叉验证高斯过程回归模型, 在不同环境温度、 不同工况下都能一定程度上得反应锂电池SOC估计结果。 对比无温度信息的PT-RPGPR 模型, 增加温度信息的T-PTRPGPR模型在25℃与35℃的温度下,SOC估计结果的RMSE与MAE变化不大, 但在45℃温度下, 模型中加入温度参数后,RMSE由8.43%减小为3.91%,MAE 由7.91%减小为3.38%,这表明增加温度因素可有效拓展训练样本, 增加SOC估计精度。

4 结 论

本文研究了基于超声传感和交叉验证高斯过程回归的锂离子电池SOC估计方法, 首先将锂电池在不同温度、 不同工况下进行充放电超声测量实验得到的数据进行分析, 发现超声TOF,PA与电池SOC的变化基本呈线性相关, 且TOF的变化相比PA的变化, 展现出与温度因素更高的相关性; 其次, 进一步对单一温度下的数据进行分析, 发现采用TOF-PA作为输入参数进行的SOC估计误差最小, 均方误差仅为3.27%, 估计性能最优; 最后, 对于在不同温度下进行试验测得的数据, 构建了增加温度参数的T-PT-RPGPR 模型, 对比无温度信息的估计模型,T-PT-RPGPR模型在45℃温度下进行SOC 估计,RMSE 与MAE明显减小, 这表明增加温度因素可有效拓展训练样本, 增加SOC估计精度。