基于金枪鱼算法的最大似然信号方位与频率联合估计

何伟嘉, 黄嘉俊, 张靖奇, 王 鹏, 白艳萍

(中北大学 数学学院, 山西 太原 030051)

0 引 言

阵列信号处理是雷达、 水声、 通信等领域中的研究热点。 在实际处理中, 如果能得到信号的空间谱, 就可以按照信号各自的能量分布, 得到信号的波达方向 (Direction-of-Arrival,DOA)。随着窄带信号方位估计模型日益完善[1], 能同时测量声压和振速的矢量水听器逐步替代了传统的标量水听器, 因此, 基于矢量水听器的信号处理方法也相继出现, 其中, 具有代表性的DOA 算法有加权子空间拟合(Weighted Subspace Fitting,WSF)[2-3]算法,多维MUSIC(Multi-dimensional MUSIC,MU-MUSIC)[4]算法和最大似然(Maximum Likelihood,ML)[5-6]算法等。1988年,Ziskind L和Max M 首次将已经提出的最大似然参数估计法在波达方向估计上应用, 但由于多维搜索最优解的庞大运算量和复杂度, 该算法很难在高要求的场合中应用。 为了适当减少运算量和计算的复杂度,Fleury等[7]提出了信号频率和方位联合估计的期望最大化方法, 而该方法由于需要通过多个一维的迭代来对信号进行搜索, 尽管估计性能优越[8], 但在多次迭代过程中, 依旧存在计算量庞大的问题。 本文所应用的角度频率联合估计模型在只对角度进行搜索的传统模型基础上增加了对频率的搜索, 因此, 在计算量和计算速度上面临更大的挑战。

随着遗传算法(Genetic Algorithm,GA)[9]的发展, 基于不同物种社会行为的群智能算法也相继提出, 分别模拟了鸟类的聚集行为和蚁群的觅食行为的粒子群优化(Particle Swarm Optimization,PSO)[10-11]算法和蚁群优化(Ant Colony Optimization,ACO)[12]算法。由于群智能算法具有寻优时间短、 算法精度高等优点, 大量学者将群智能算法在ML-DOA 模型中加以应用来解决模型中存在的不足,其中有松鼠搜索算法(Squirrel Search Algorithm,SSA)[13],正余弦算法(Sine Cosine Algorithm,SCA)[14],原子搜索优化(Atom Search Optimization,ASO)[15-16]算法,人工蜂群(Artificial Bee Colony,ABC)[17]算法等。 经过这些算法优化后的模型可以有效减少迭代时的计算量, 并使其具有良好的性能, 尽管一些算法对于性能的提高有所帮助, 但是依旧存在算法中固有的过早收敛和速度不够快等问题。 在以往的研究中, 优化算法大多应用在DOA角度估计优化中, 而在频率估计优化中应用较少。 其中具有代表性的研究有单泽彪等[18]提出的将序列二次规划应用于最大似然函数的联合谱估计算法, 张志成等[19]将人工蜂群算法优化似然函数, 实现了DOA和频率的联合估计。 因此, 本文针对频率估计应用较少的问题, 提出了用金枪鱼优化(Tuna Swarm Optimization,TSO)[20]算法对模型进行角度频率联合估计。

TSO是一种通过金枪鱼的两种群体觅食行为提出的群智能算法。 金枪鱼为了找到它们的猎物,通过两种觅食途径来进行捕猎, 即螺旋方法进食和把食物做为参考点形成抛物线进行合作觅食。TSO算法是通过在搜索空间中随机生成总体, 随后在迭代个体中随机选择两种觅食方式中的一种来进行觅食的智能算法。

本文将TSO 应用到频率方位联合估计的ML-DOA中, 提出基于金枪鱼算法的最大似然信号方位频率联合估计, 并通过仿真发现该算法与其他智能算法相比具有收敛精度高、 收敛速度快、陷入局部最优可能性小以及搜索时间成本少等优势。

1 方位频率联合估计的阵列信号模型和最大似然估计

1.1 频率方位联合估计的阵列信号模型

假设不同方向的D个远场窄带信号源以角度(θ1,θ2,…,θD}入射到由M个矢量水听器组成的均匀线性阵列上, 其中M＞D, 则阵列接收到的矢量信号可以由下式表示

1.2 最大似然估计

在等间距阵列中进行K次均匀采样, 采样数据的频率角度联合概率密度函数可以表示为

2 基于TSO算法的信号方位与频率联合估计

2.1 金枪鱼算法

金枪鱼作为海洋中的捕食能手, 使用“群体觅食”的方法来选择不同的觅食策略进行捕食。 第一种策略是螺旋式觅食: 金枪鱼群通过形成一个紧密的螺旋形结构来追逐猎物, 同时附近的鱼会接连调整方向, 最优个体甚至能够在猎物追寻中与金枪鱼群互相交换信息, 最终聚集为一个有相同进攻目标的金枪鱼群体, 开始捕猎。 第二种策略是抛物线型的合作觅食: 其中之一是金枪鱼以食物为参考点, 形成抛物线进行进食; 另外一种是金枪鱼通过在自己周围寻找食物进行觅食, 并假设在概率均为50%的情况下两种方式同时执行[17]。

金枪鱼通过上述两种觅食方法对所有个体进行不断更新和计算, 直到满足最终条件返回最优个体和相应的适应度值, 结束觅食。

2.2 基于TSO算法的信号方位频率联合估计

本节中, 基于最大似然估计原理, 将TSO 算法应用在信号方位与频率的联合估计中, 令X=(θ,f), 具体步骤如下:

1) 参数初始化

模型中信号方位θ的寻优范围是[0°,180°],信号频率f的寻优范围是[1 k Hz,2 k Hz], 算法中种群分配自由参数α=0.7,z=0.05, 算法维度为信号源个数。

2) 种群初始化

金枪鱼的初始位置Xiint=rand·(ub-lb)+lb,i=1,2,…,NP, 代表第i个信号的初始角度和频率,ub和lb分别为搜索空间的上界和下界,NP为金枪鱼种群的数量,rand为从0到1的均匀分布的随机向量。

3) 计算个体适应度

通过计算金枪鱼的适应度值并更新α1,α2,p, 随后将随机值和参数z进行比较, 如果方位角和频率的随机值小于参数值z, 对此方位角和频率依据步骤2)中的初始化公式进行位置更新。

4) 位置更新

在金枪鱼的两种随机觅食策略的位置更新中,当rand＜0.5时, 通过使用螺旋式策略来更新位置。 再继续判断t/tmax是否小于随机值, 若小于随机值, 则进行全局搜索位置更新。 随着迭代次数的增加, 一旦t/tmax大于等于其设定的随机值, 则采用局部搜索位置更新。

螺旋式位置更新如下

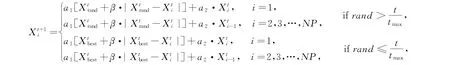
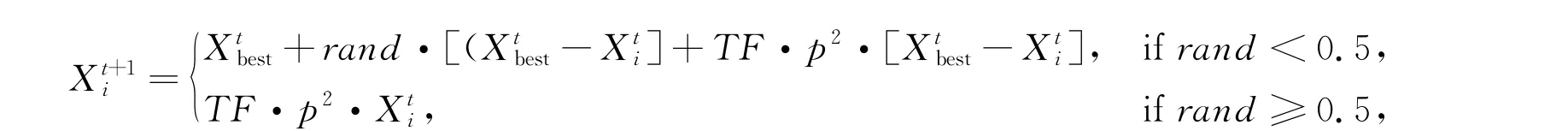
5) 终止条件判断

如果迭代次数超过最大迭代次数, 则终止,输出方位角所对应的最优适应度值和其位置(估计的方位角和频率)。 反之, 则返回到计算适应度值进行新一轮判断。

按照以上步骤可得出待估计的方位角和频率。

3 实验与仿真

在本次实验中, 假设由8个矢量水听器组成均匀线阵, 信噪比为20 dB, 快拍数为300, 种群规模为20, 最大迭代次数为100, 分别记录100次蒙特卡罗实验的结果。

3.1 适应度分析

在实验条件不变的情况下, 分别利用TSO,ASO,SSA,SCA,ABC算法优化L(^θ,^f), 对信号方位和频率进行估计。 表1为4种优化算法的其他参数设置, 其中S为种群个数,C为最大迭代次数,a1为常数,z为选择哪种觅食方式的概率,a1为深度权重,β为乘数权重,pd为移动策略的出现概率,dg为比例因子,GC为滑动系数。

表1 不同优化算法的参数设置Tab.1 Parameter settings of different optimization algorithms

当信号源分别为1个([30°,1 k Hz])和2个([30°,1 k Hz], [60°,1.3 k Hz])时, 利用SSA,SCA,ASO,ABC和TSO算法优化L^(θ,^f), 记录100次蒙特卡罗实验得到的平均值、 最小值和标准差, 并列表对3种衡量标准进行比较, 如表2所示。由于适应度函数是目标函数的直观体现, 即平均值、 最小值和标准差适应度值均越接近于零, 说明估计得到的角度和频率越接近真实值, 因此, 由表2可以看出,5种不同优化算法在1个和2个信号源时所得到的平均值、 最小值和标准差均是TSO算法的值最接近零。 因此,TSO算法在模型中有着较高的稳定性和准确的频率角度估计值。

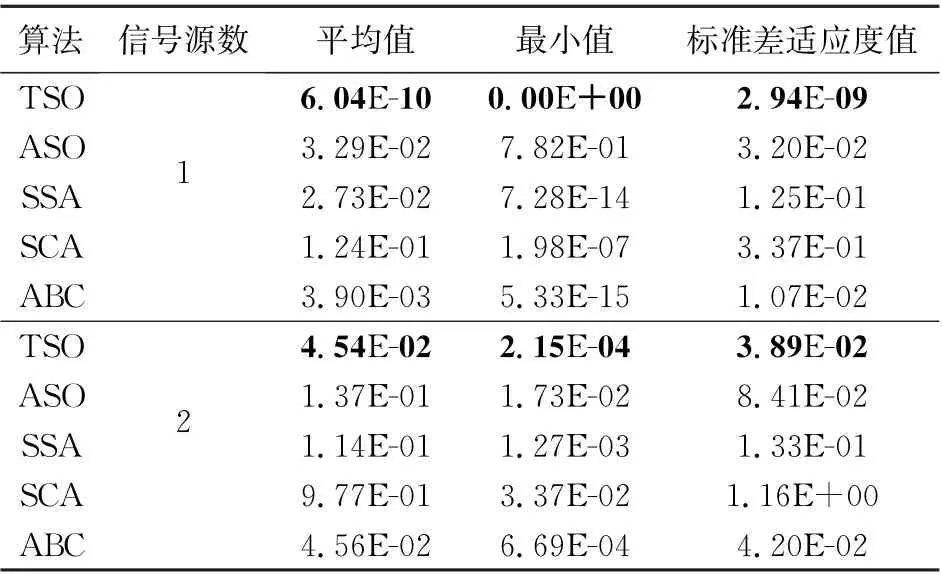
表2 TSO算法与其他算法性能比较Tab.2 Performance comparison of TSO algorithm with other algorithms

3.2 方位频率估计

通过计算方位、 频率的估计值和真实值的相对误差来反应不同算法对角度频率估计的准确,即定义方位和频率的评价标准为

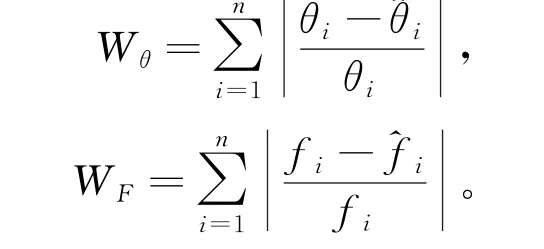
通过评价Wθ和WF来判断估计精度, 即Wθ和WF值越小, 说明由该算法估计的方位和频率越接近真实的角度和频率值, 优化效果越好。 在实验条件保持不变时, 设置在单个声源的情况下计算不同算法所得的Wθ和WF值, 结果如表3所示。 通过与其他算法对比, 发现TSO 算法在估计中有着更小的Wθ和WF值。 因此, 该算法对方位和频率的估计有着较高的精度。

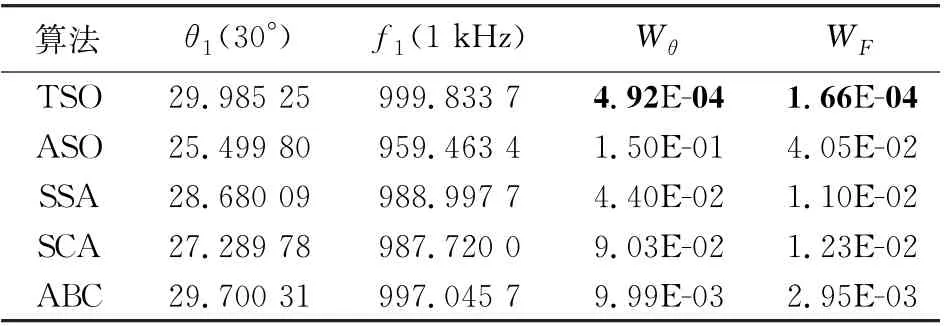
表3 声源个数为1时不同算法下的误差值Tab.3 Error value under different algorithms when the number of sound sources is 1

3.3 收敛性能

收敛速度和收敛精度也是衡量算法的重要指标。 图1绘制了当信号源个数分别为1和2时所得出的5种智能算法的收敛曲线。 从图1中看出,当声源个数为1时,TSO 算法在整个迭代过程中均有着最低的适应度值, 最快的收敛速度和最高的收敛精度。 当声源个数为2时, 虽然TSO 算法在迭代初期的迭代速度略慢, 但随着迭代次数的增加,TSO算法的收敛速度逐渐超过其他算法的收敛速度。

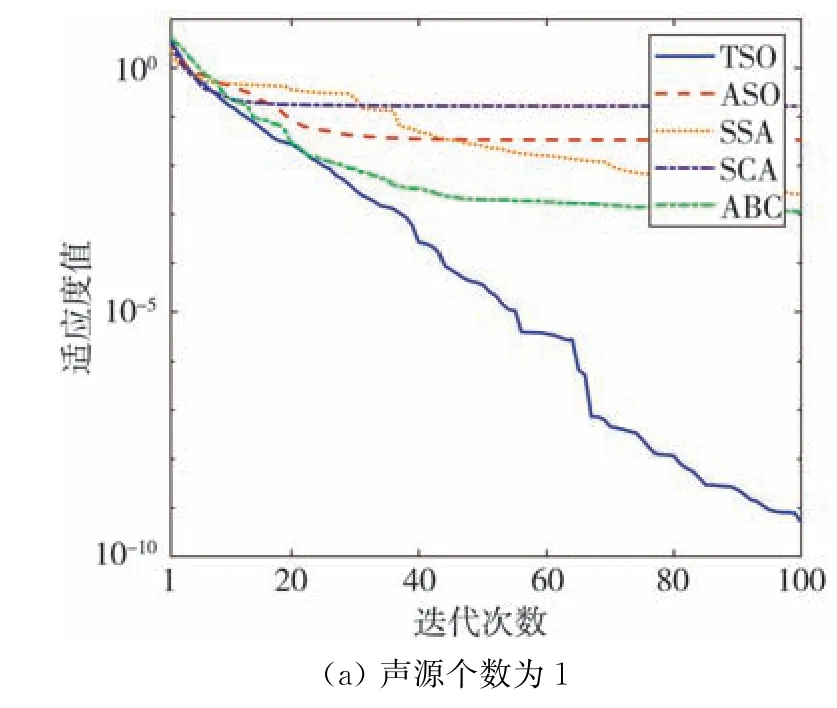
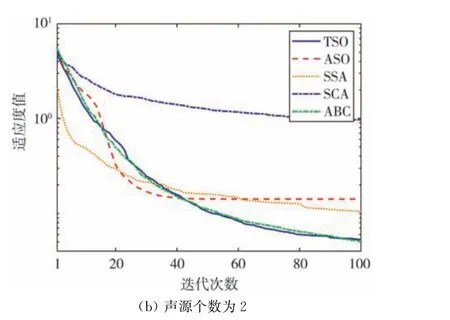
图1 不同声源个数时TSO算法和其他优化算法收敛性能的比较Fig.1 Comparison of the convergence performance of theTSO algorithm and other optimized algorithms withdifferent numbers of sound sources

由图可知,TSO 算法与ABC算法迭代速度相当, 迭代中的收敛精度相近, 但在误差实验中,TSO算法有着更小的误差。TSO算法与其他4个算法相比,TSO算法有着快的收敛速度和低的收敛精度。

3.4 统计性能

为比较声源个数不同的情况下5种算法对角度频率联合估计的统计性能, 分别在1个声源和2个声源的情况下改变信噪比, 并用均方根相对误差(Root Mean Square Relative Error)作为衡量尺度来对比算法的估计性能, 公式如下

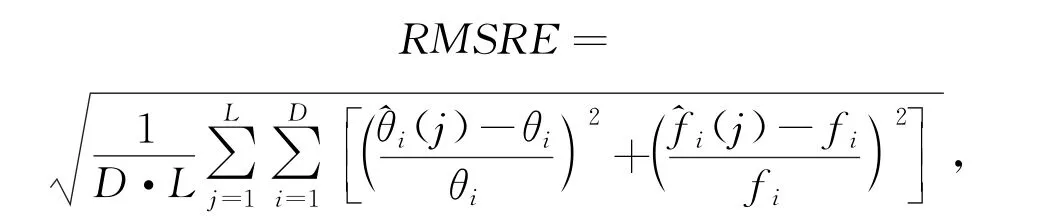
式中:L和D分别为试验次数和信号数。5种算法的初始种群数均为20, 对比不同声源个数下的RMSRE值, 结果如图2所示。

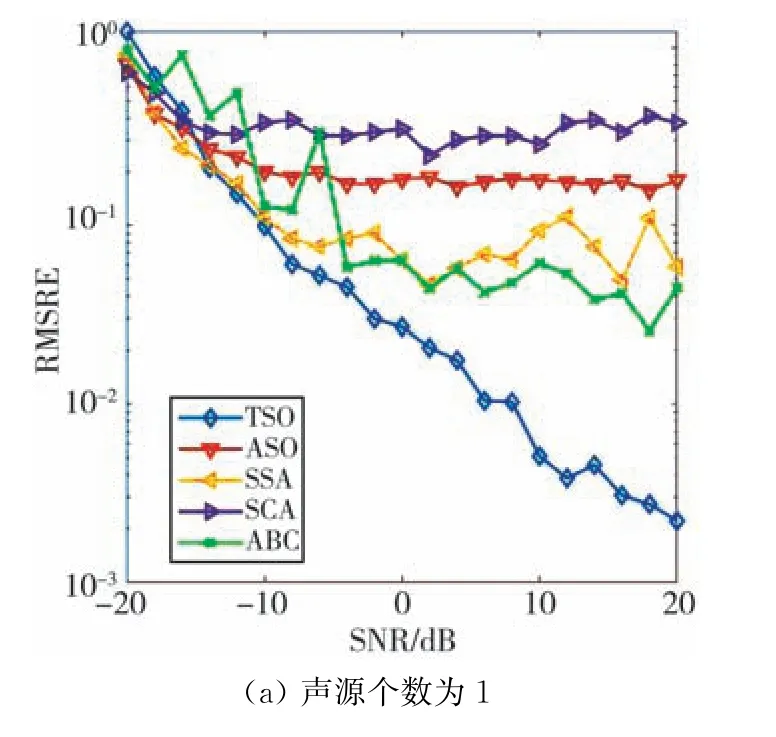
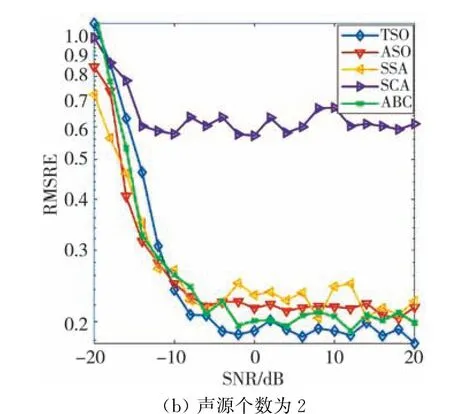
图2 不同声源个数情况下的DOA估计的均方根相对误差随信噪比(dB)的变化曲线Fig.2 The variation curve of the relative error of the root mean square of the DOA estimation with the number of sound sources and the signal-to-noise ratio(dB)

从图2可以看出, 在信号源个数为1 时,TSO算法在信噪比为-20 dB～-15 dB时误差稍大, 随着信噪比的增加,TSO 算法能稳定保证高的估计精度和低的RMSRE。 在信号源个数为2时,5种优化算法整体的RMSRE有所上移, 虽然TSO算法在低信噪比时不如其他算法的误差稳定, 但可以看出TSO算法随着信噪比增加可以迅速达到低的RMSRE。

4 结 论

本文通过将金枪鱼算法与最大似然角度频率估计相结合, 降低了计算复杂度, 减少了计算量,保证了该算法的有效性。 通过与ASO,SSA,SCA,ABC 4种算法的比较, 发现在不同信噪比和迭代次数情况下,TSO 算法有着更小的适应度值、 更快的收敛速度和更低的RMSRE, 更接近入射信号的角度和频率。 因此,TSO 算法在信号方位和频率估计中有着良好的估计性能, 能满足在实际中的精度要求, 具有一定的工程实用性。