一类广义不稳定时空分数阶薛定谔方程的近似解
2023-01-16洪宝剑
洪宝剑
(南京工程学院 数理学院,江苏 南京 211167)
众所周知,许多自然科学和工程问题都可以归结为非线性方程的求解,尤其是分数阶方程几乎应用于社会生活的每一个领域.因此,研究非线性方程的解就成了国内外学者需要关注的首要问题.迄今为止,人们提出了寻求非线性方程精确解及近似解的各种方法,如贝克隆变换法、约束方程法、同伦分析法、Adomian展开法、变分迭代法等[1-7].近年来,Laplace变换法被广泛应用于各类非线性系统的求解[8-10].论文将借助Adomian多项式和同伦摄动的理论,将Laplace变换法应用于一类广义分数阶薛定谔方程,得到较好的结果.
考虑下列广义不稳定时空分数阶薛定谔方程
(1)
其中:u=u(x,t),a,γ为非零常数,v(x)为实函数.
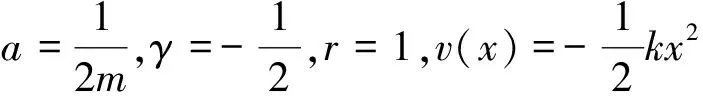
1 几个定义
为了方便后面计算,关于分数阶导数和Laplace变换,给出几个定义[7,23].
定义1一个实函数f(t),当μ∈,t>0时,若存在实数p>μ,使得f(t)=tpf1(t),其中:f1(t)∈C[0,∞),则称f(t)∈Cμ,若f(n)(t)∈Cμ,n∈,则称
定义2函数u(x,t)关于t的Caputo分数阶导数定义为[13,18,23]
(2)
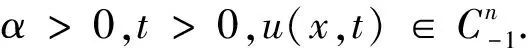
Caputo分数阶导数具有下列性质
DαC=0,C为常数,
Dαf[u(x)]=fuu(α)(x).

(3)
2 近似解的推导
关于Laplace变换迭代法的具体步骤可参阅文献[8-10,24-27],对(1)进行简单变换得
(4)
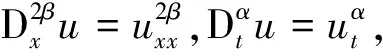
(5)
(6)
对(6)两边作Laplace逆变换
(7)
构造同伦方程
(8)
显然当p:0→1时,u:u0→u,若令
(9)
则(1)的精确解为
(10)
比较p的同次幂,构造迭代式
(11)
其中:An是(8)中非线性项N(u)=|u2r|u通过Adomian多项式线性化后的第n项[4,13,21].
(12)

(13)
当r≠1时,若u为实函数,则按牛顿二项公式展开,若为复函数,则按三角形式展开,均可得到An.再由(10),(11)式就可以得到方程(1)的各级近似解或精确解,下面讨论(1).
情形1当r=1,v(x)=-cos2x,u0=sinx时,有
(14)
由(11),(13)式,有
u0=sinx.
(15)
(16)
[a2sin(x+2πβ)+4a(2γ+1)sin2xsin(x+πβ)-2asin(x+πβ)+
(17)
…
(18)
方程(14)的一个n级近似解为
(19)

(20)

情形2当v(x)=2λ,u0=eix时,有
(21)
构造迭代式
(22)
有
u0=eix.
(23)
(24)
(25)
(26)
…
(27)
方程(21)的一个n级近似解为
(28)
所以方程(21)的一个精确解为
(29)
注2当γ=a,r=1,λ=0时,u1,u2,u3与文献[23]中的结果一致.当γ=1,λ=0时,Un表达式比文献[13]中的结果(3.18)标准.当γ=a=0.5,r=1,λ=0时,(29)式转化为文献[28]中的(49)式.
情形3当v(x)=k(1-x2),u0=x2时,有
(30)
接下来尝试对迭代式的构成方式进行修正.考虑到u(x,t)=φ(x,t)eiψ(x,t),|u(x,t)|=|φ(x,t)|,利用文献[23]中的修正思想,构造迭代式
(31)
有
u0=x2.
(32)
(33)
k2x2-2k2x4+k2x6],
(34)
4γk2x4r+2+8γk(γ-k)x4r+4-4γk(2γ-k)x4r+6+4γ2kx8r+2+
4γ2(2γ-k)x8r+4+k2(2γ-k)x8-k2(4γ-3k)x6+k2(2γ-3k)x4+k3x2].
(35)
…
方程(30)的近似解为
Un=u0+u1+u2+u3+….
3 数值分析
借助Mathematica软件,表1,2和图1,2分别对方程(1)的n级近似解(28)式和精确解(29)式进行对比和数值模拟,分别讨论当α=1,β=1,γ=1,a=1,r=1,v(x)=0时的整数阶方程情形和当α=0.5,β=0.8,γ=1,a=1,r=1,v(x)=0时的分数阶方程情形.图3,4对方程(30)当a=k=r=1,γ=0.5时,在α,β不同参数取值的近似解的实部和虚部进行了模拟.

表1 当α=1,β=1,γ=1,a=1,r=1,v(x)=0时,(28)和(29)虚部的数值结果
注3Absolute Error精确位数取为小数点后20位,迭代到50次后误差几乎消失了.
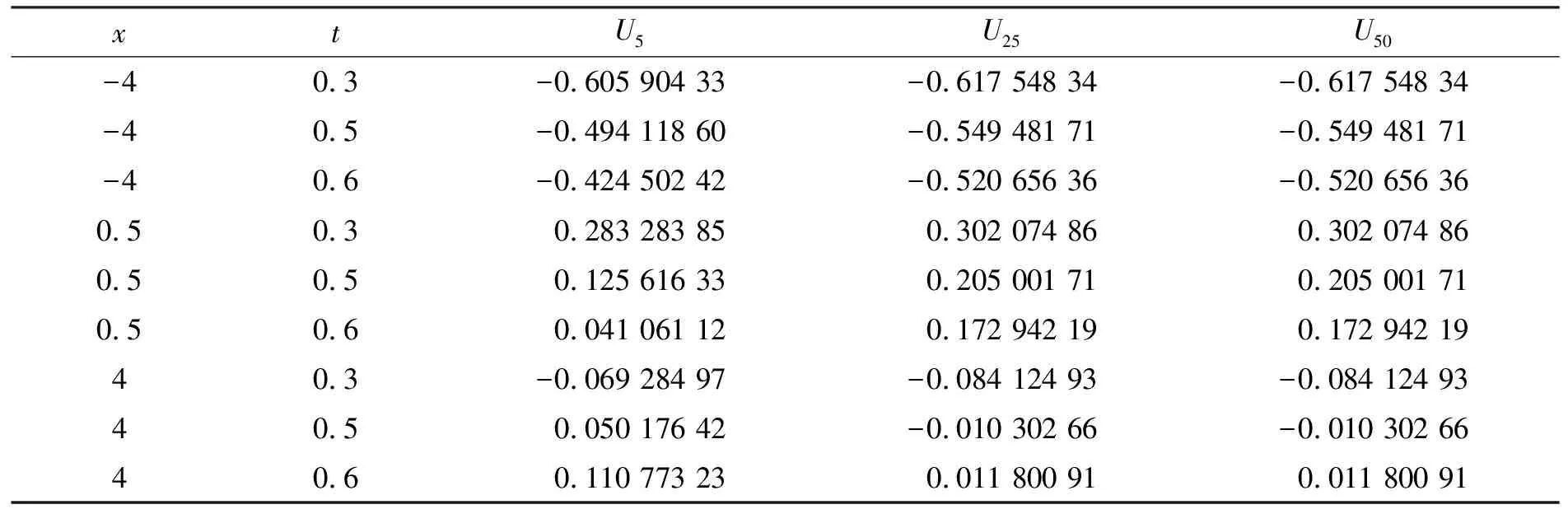
表2 当α=0.5,β=0.8,γ=1,a=1,r=1,v(x)=0时,(28)和(29)实部的数值结果
部分数值模拟结果如图1~4所示.
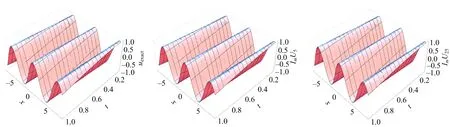
图1 当α=1,β=1,γ=1,a=1,r=1,v(x)=0时,精确解与近似解迭代5,25次虚部图
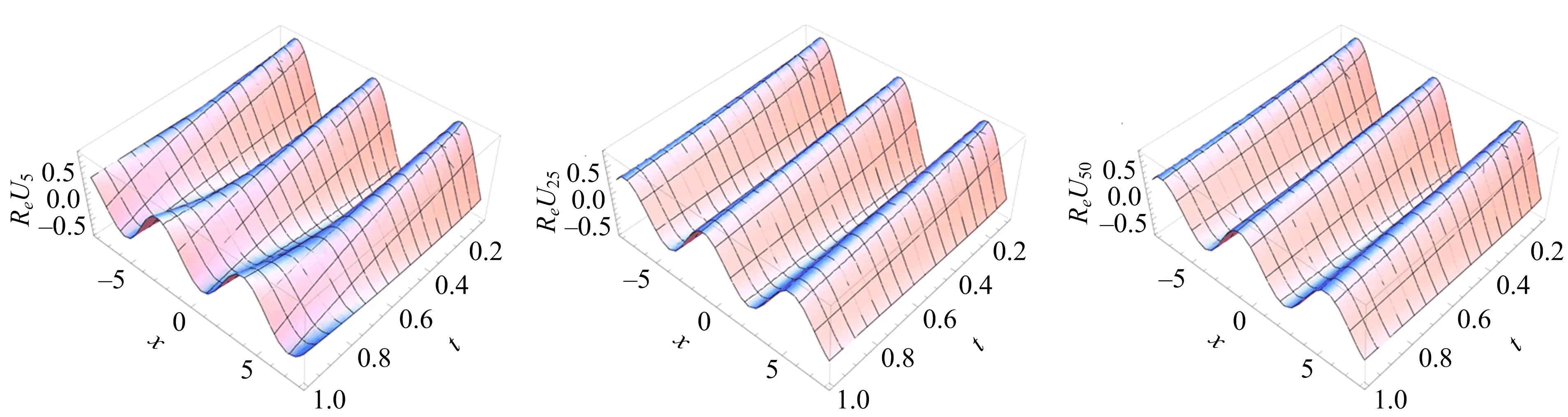
图2 当α=0.5,β=0.8,γ=1,a=1,r=1,v(x)=0时,近似解迭代5,25,50次实部图
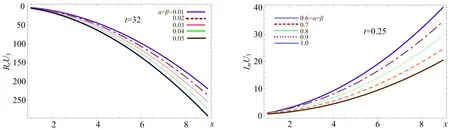
图3 不同参数下各级近似解实部变化 图4 不同参数下各级近似解虚部变化
图1,2的数值结果表明,U25,U50已经和精确解靠得很近.在图3,4中随着α,β的增大,实部和虚部函数稳定地向α=β=0.05及α=β=1靠拢,因而该迭代算法有效.
4 结束语
论文通过将Laplace变换和同伦摄动法相结合,求解一种不稳定时空分数阶薛定谔方程,得到了方程的各级近似解,并进行了误差分析和数值模拟.研究结果表明,这一方法对于薛定谔类复偏微分方程近似解的处理规范有效.
