基于位移梯度法的深基坑桩锚支护结构动态稳定性分析
2023-01-16赵元基王正振熊泤哲
周 勇, 赵元基, 王正振, 熊泤哲
(1. 兰州理工大学 甘肃省土木工程防灾减灾重点实验室, 甘肃 兰州 730050; 2. 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心, 甘肃 兰州 730050; 3. 兰州理工大学 土木工程学院, 甘肃 兰州 730050;4. 澳门大学 科学技术学院, 澳门 999078)
基坑的动态稳定性分析为评价支护结构的安全性以及经济性提供了重要的依据,而滑裂面的搜索模型以及安全系数的计算理论是基坑动态稳定性分析中的两大重要内容.
滑裂面的搜索方法主要分为三大类:第一类方法是建立在传统的极限平衡理论上[1],通过搜索算法找出安全系数最低的滑裂面.朱彦鹏等[2]在极限平衡理论的基础上提出了圆弧滑裂面的搜索方法.其计算方法是假设滑裂面经过墙趾且滑裂面是圆弧形,将滑动矩和抗滑力矩的比值作为安全系数.周勇等[3]在圆弧滑裂面的基础上研究了考虑附加应力作用的桩锚支护结构稳定性与位移的关系,将圆弧滑裂面搜索方法的应用范围进一步扩大.第二类方法是建立在有限元的计算结果上,通过位移场或应力场搜索滑裂面.袁维等[4]基于位移场分析临界滑动面,通过找到直线上位移变化率最大的位置点作为滑裂面的位置.李忠等[5]基于应力场并通过多种群遗传算法搜索滑裂面的位置,通过多种群遗传算法为安全系数的计算提供滑裂面,并将安全系数作为影响适应度函数的变量,搜索出安全系数最低的滑裂面.第三类方法是在强度折减法的基础上提出的滑裂面的搜索方法.该方法通过对土体强度参数不断折减,将最终形成的贯通的塑性区作为滑裂面.王伟等[6]认为在进行边坡稳定性计算时不能忽略张拉破坏,并提出了张拉-剪切渐进式破坏的强度折减法.戴自航等[7]在土坡稳定性数值分析中通过二次开发加入张拉-剪切复合破坏材料模型并以剪切破坏区与张拉破坏区贯通的区域作为滑裂面.传统的极限平衡法很难反映基坑开挖的时空效应对滑裂面的影响.强度折减法虽然可以考虑时空效应,但是计算结果可能会出现很大的塑性区,导致滑裂面不能准确得到.
安全系数的计算理论主要分为两种:一种是极限平衡理论,即将抗滑力和下滑力的比值作为基坑的安全系数.这种方法在经典的边坡稳定性理论中被提出和应用,如Bishop法[8]、圆弧法[9]等.随着有限元的不断推广和应用,这种计算理论又与有限元相结合.曾亚武等[10]提出将边坡稳定性分析的有限元法和极限平衡法相结合,利用有限元计算的应力场求出条分底部的应力,并根据极限平衡法的概念得出边坡稳定性安全系数.另一种方法是对土体参数进行不断折减,当达到临界状态时,将折减系数作为基坑的安全系数.这种方法在1975年由Zienkiewicz等[11]首次提出.随着有限元软件的发展和推广,强度折减法也得到了发展.唐晓松等[12]通过双强度折减法分析了加筋土边坡的稳定性.但是,强度折减理论在基坑边坡临界状态的评判标准上存在争议,所以在实际应用中需要设计人员根据经验选取临界状态的评判标准.
本文在以上研究成果的基础上,提出了基于切向位移梯度法和位移场的滑裂面的搜索模型.同时结合传统的极限平衡理论,采用抗滑力和下滑力的比值计算安全系数,并在计算安全系数的过程中考虑了滑裂面浅层部位的土体由于张拉破坏对抗滑力产生的不利影响.
1 基于切向位移梯度法的滑裂面搜索模型
1.1 模型建立
根据现场施工经验,支护结构在发生整体失稳破坏时,桩后土体内会形成一条滑裂面.滑裂面上方的土体为滑动体,下方的土体为非滑动体.在临界情况下,滑动体和非滑动体之间发生相互错动.这种错动形式在数学上表现为滑动体与非滑动体之间形成的剪切带附近的土体的切向位移梯度在某一方向上存在极大值.
根据基坑整体失稳破坏的形式,本文建立了一种基于切向位移梯度法的滑裂面搜索模型(如图1所示).本模型假设滑裂面经过支护结构的墙趾[2,13],并假设滑裂面起始点处的切线方向与水平方向45°+φ/2夹角.在搜索滑裂面时首先沿着起始点的切线方向延伸一小段距离,获得滑裂面上的第二节点.从第二个节点开始,采用切向位移梯度法搜索节点位置处切向位移梯度最大的方向,并顺着此方向延伸至滑裂面的第三个节点.反复执行最后两步,直至延伸到基坑顶面.
1.2 切向位移梯度函数的构建
切向位移梯度的计算简图如图1所示.Pn表示

图1 滑裂面切线方向计算简图Fig.1 Schematic diagram of tangential direction of slip surface

(5)
Δτ=u′tcosθ+v′tsinθ-u′bcosθ-v′bsinθ
(6)
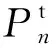
1.3 滑裂面上离散点坐标的确定
在搜索出了切向位移梯度最大的方向θn之后,将搜索出的方向作为滑裂面上Pn点的切线方向,并沿着Pn点的切线方向从Pn点延伸Δs长度至Pn+1点.将上述步骤反复进行,直至计算到基坑顶面,即可求解出整个滑裂面.计算公式如下
式中:Δs为滑裂面上相邻点之间的距离;由于墙趾位置在进行位移梯度计算时偏移点可能会位于土体以外,造成较大的计算误差,因此θn初始值θ1取45°+φ/2.
2 安全系数的计算模型
首先,本文在计算安全系数时考虑了张拉破坏对安全系数造成的不利影响,因此需要确定张拉破坏和剪切破坏的判定条件.其次,本文确定的滑裂面是非规则形状,因此需要建立取矩中心的搜索模型.最后,在确定了滑裂面、张拉破坏区和剪切破坏区以及取矩中心后才能计算安全系数.
2.1 张拉破坏与剪切破坏的判定条件
在基坑的开挖过程中,浅层土体由于自重应力产生的围压较小.同时,在基坑的开挖过程中浅层土体又要承担一定的剪切荷载,导致浅层土体的应力比η很大(其中,η=q/p,p为对应位置土体的围压,q为对应位置土体的广义剪应力).过大的应力比使浅层土体发生张拉破坏.传统的计算理论中考虑这一部分土体的抗剪贡献,但事实上这部分土体不能提供抗剪贡献.为了划分张拉破坏区和剪切破坏区,本文采用修正剑桥模型理论[14],将应力比作为张拉破坏与剪切破坏的判定条件.根据修正剑桥模型理论,在正常固结土条件下,土体的应力比达到M时土体将发生破坏;在超固结土条件下,当η介于M和Mf之间时,土单元体发生剪胀,当η达到Mf时土体破坏[15](如图2所示).剪胀关系的公式如下
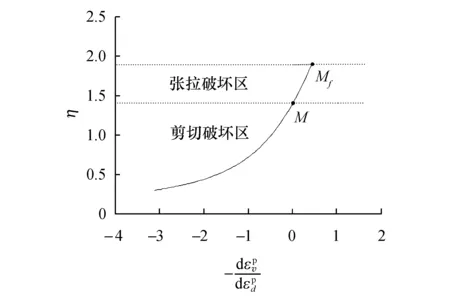
图2 固结土剪胀关系Fig.2 Dilation curve of consolidated soil
(9)


(10)
式中:φ为对应土层的摩擦角.
2.2 抗滑力矩及下滑力矩的取矩中心的搜索模型
取矩中心的空间位置直接影响到下滑力矩和抗滑力矩的计算结果,并最终影响到安全系数的计算结果,对基坑动态稳定性的评估造成影响.因此需要建立与滑裂面形状相适应的取矩中心的搜索模型.
由于基坑在发生整体失稳时,滑裂面上方的滑动体可以近似地认为是一个整体,因此可采用理论力学[17]中求解刚体瞬心的方法搜索取矩中心.假设滑裂面上有n个节点坐标(即式(7)和式(8)求解出的滑裂面上离散点的坐标),则理论上可以获得n个节点的切线方向.将这些节点两两组合,计算出n×(n-1)个瞬心.通过统计这些瞬心的分布可以发现大多数瞬心集中在很小的范围内,因此可以取瞬心最集中的位置作为取矩中心.计算公式如下
将两条法向的直线方程联立得
(11)
化简得

2.3 安全系数计算模型
根据《支挡结构设计》[18]以及《深基坑支护技术指南》[19],并结合本文提出的滑裂面搜索模型,稳定性系数Ks可以按下式进行计算
(14)
式中:MR为抗滑力矩总和;MT为下滑力矩总和;MR1为土体抗剪提供的抗滑力矩;MR2为锚索提供的抗滑力矩;MR3为支护结构底部的水平推力设计值产生的抗滑力矩;MT1为土体自重引起的滑动力矩;MT2为附加荷载引起的滑动力矩.
MT1的计算采用瑞典条分法,将计算出来的滑动体沿着x方向条分,将每条土体的自重对取矩中心求矩并累加,计算出滑动体由于自重所产生的下滑力矩.计算模型如图3所示,计算公式如下
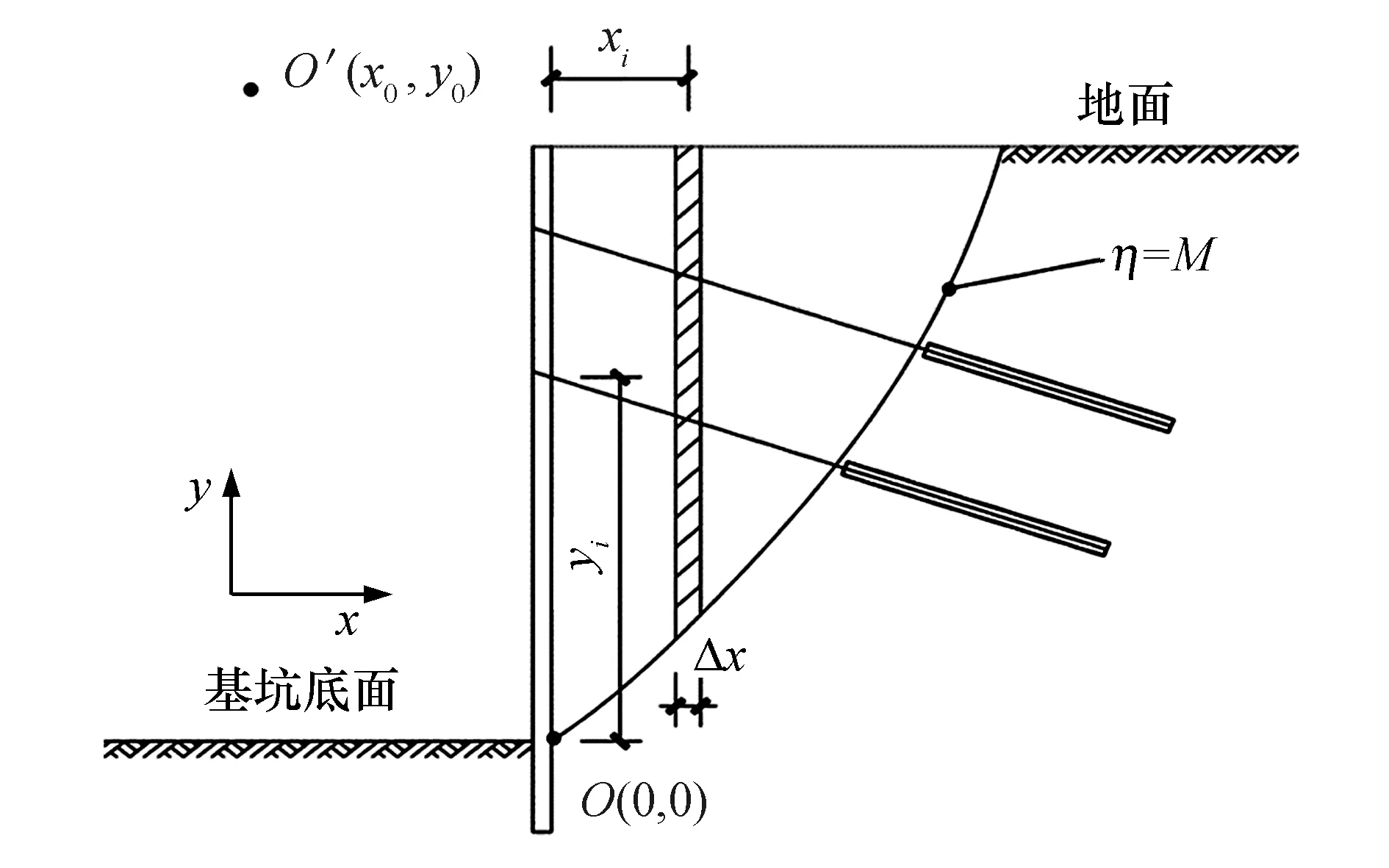
图3 下滑力矩MT1计算图示Fig.3 Calculation diagram of sliding moment MT1
(15)
其中:ye为基坑边坡顶面坐标;Δx为土条划分的单
位长度(又可表示为Δs·cosθi);x0、y0分别为取矩中心的横纵坐标;xi、yi分别为第i根土条底面的中心点坐标;γ(y)为对应深度处土体的重度;O′为取矩中心.
MT2的计算模型如图4所示,计算公式如下
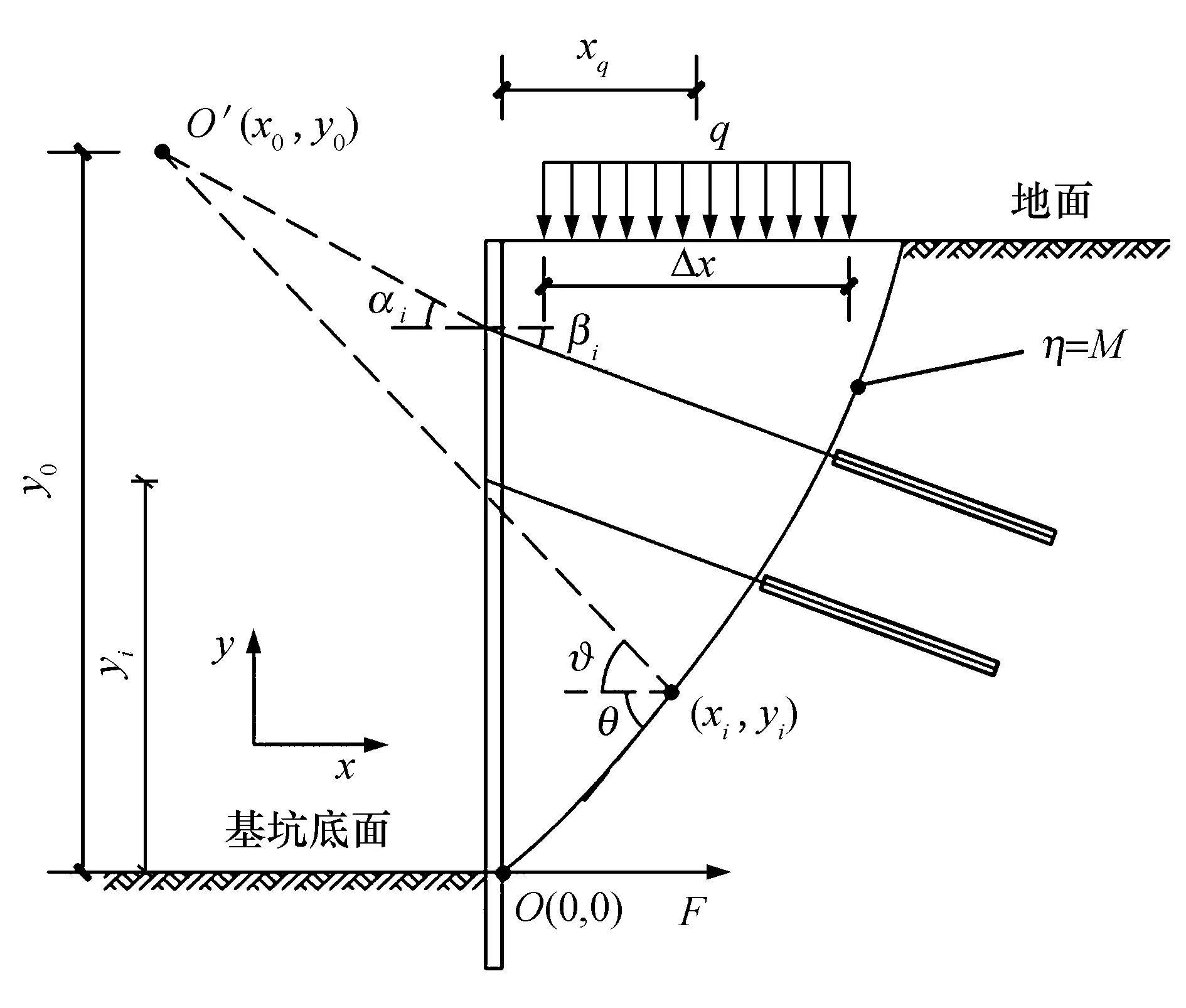
图4 下滑力矩MT2及抗滑力矩MR1、MR2、MR3计算图示Fig.4 Calculation diagram of sliding moment MT2 and anti-sliding moment MR1,MR2,MR3
MT2=q0·Δx·(xq-x0)
(16)
式中:q0为均布载荷集度;Δx为均布载荷的作用范围;xq为均布载荷合力作用点的横坐标.
MR1的求解主要依赖于Abaqus中计算出来的位移场、应力场以及用户自定义子程序计算出来的土体状态参量.土体抗剪承载力按照莫尔-库伦强度理论进行计算.计算模型如图4所示,计算公式如下
式中:θi为滑裂面的切线方向和水平方向之间的夹角;ϑi为滑裂面上的计算点和取矩中心的连线与水平方向的夹角;p(xi,yi)为对应力场进行线性插值得到的有效法向应力;ci、φi按照地质勘探结果取值.E(xi,yi)为土体状态参量,当对应位置土体的应力比超过M时(即对应位置土体发生了张拉破坏,不考虑抗剪贡献),E取0,否则E取1.
MR2为预应力锚索极限抗拉承载力产生的抗滑力矩,计算模型如图4所示,计算公式如下
(20)
(21)
式中:Ti为第i根锚索对应的极限抗拉承载力;αi为桩头与取矩中心连线方向与水平方向的夹角;βi为第i根锚索与水平方向的夹角;yi为第i根锚索的纵坐标.
MR3为支护结构底部的水平推力设计值产生的抗滑力矩,计算模型如图4所示,计算公式如下
MR3=F·y0
(22)
式中:F为支护结构底部的水平推力设计值.
将上述MR1、MR2、MR3、MT1、MT2的计算结果代入式(14)即可得到对应工况下基坑的安全系数.
3 模型的实现步骤
由于本文基于数值应力场、位移场等有限元计算结果分析基坑的动态稳定性,因此首先需要对基坑开挖的全过程进行有限元分析,并将计算结果导入MATLAB中.接着,基于本文提出的位移梯度法搜索基坑每一个施工步骤的滑裂面.最后,根据计算出的滑裂面以及导入MATLAB的有限元计算结果计算每个施工步骤基坑的安全系数,并分析其动态稳定性.
3.1 有限元分析及数值计算结果的导出和导入
用Abaqus模拟整个施工过程.有限元建模步骤如下:
1) 在Part模块中输入土体、支护桩以及锚索的几何参数.
2) 在Property模块中定义土体材料参数,采用Mohr Coulomb Plasticity模型作为土体材料的屈服准则.另外,在Property模块中还要定义土体的用户定义子程序的输出变量(这些变量用于输出土体的应力比及有效法向应力).
3) 在Assembly模块中将土体、支护桩以及锚索组装在一起.
4) 在Step模块中根据工况定义分析步.
5) 在Interaction模块中定义桩土之间的摩擦并利用生死单元模拟整个基坑开挖过程中土体单元的变化情况.
6) 在Load模块中施加边界条件、自重荷载、均布荷载以及锚索预应力.
7) 在Mesh模块中对所有部件划分网格并在滑裂面可能出现的位置对网格进行适当加密.
8) 在Job中提交任务.
有限元计算结束后,将网格节点数据以及计算出来的应力场、位移场、自定义输出变量场导出.网格节点数据可以在inp文件中获取.应力场、位移场、自定义输出变量场数据可以通过Report Field Output工具导出.
用MATLAB中的Import Data工具将网格节点数据、应力场数据、位移场数据、自定义输出变量场数据导入到MATLAB的工作区中.
3.2 应用位移梯度法搜索滑裂面
在完成网格信息、土层信息以及有限元计算结果的导入之后,即可应用位移梯度法搜索滑裂面.本算法首先需要确定滑裂面上的节点,然后在节点之间连线并生成滑裂面.滑裂面的搜索流程如图5所示,滑裂面的搜索过程大体分为3步:

图5 滑裂面搜索流程图Fig.5 Flow chart of sliding surface research
1) 滑裂面上前两个节点的获取:取墙趾位置作为滑裂面上的第一个节点,从第一个节点开始沿着45°+φ/2方向延伸Δs至滑裂面上的第二个节点(其中φ为第一个节点所在土层的土体的摩擦角).
2) 滑裂面上其它节点的获取:从第二个节点开始,搜索切向位移梯度最大的方向.将对应坐标位置处的水平位移和竖向位移代入式(5)和式(6)中,即可获得对应方向上的切向位移梯度.在0°~90°范围内搜索切向位移梯度最大的方向作为该点的切线方向,并将方向角代入式(7)和式(8)中,即可获得第三个节点坐标.
为得到式(6)中对应空间位置处的水平位移u以及竖向位移v,可以将该点所在的单元体的四个节点的位移代入拉格朗日多项式[20]求解,其中ξ、η为相对于四节点单元体几何中心的局部坐标,计算简图如图5所示,求解公式如下
式中:Ni为插值函数,表示方法如下
(25)
ξ0=ξiξ
(26)
η0=ηiη
(27)
式中:ξ、η为局部坐标;ξi、ηi为节点处的局部坐标,具体表示形式如图6所示.

图6 四节点单元体局部坐标Fig.6 Local coordinate of four-node unit body
反复上述两个步骤,直至计算到地面标高处.至此,滑裂面上所有的节点均可以得到.
3) 滑裂面的获取:将滑裂面上的所有节点按顺序连线,即可获得滑裂面.
3.3 考虑张拉破坏的安全系数算法
1) 划分张拉破坏区与剪切破坏区
通过Abaqus中的UVARM[21-22]用户定义子程序划分桩后土体的张拉破坏区与剪切破坏区.由于张拉破坏区的土体无法承受剪切荷载,因此这部分土体无法提供抗滑力矩,在进行安全系数计算时应该将滑裂面上应力比超过M的土体状态参量取零.
2) 确定非圆弧滑裂面的取矩中心
将滑裂面上所有节点的坐标及其节点的切线方向角代入式(12)和式(13)中进行计算,计算结果中可能会出现一些不合理的解,这些解不仅会影响计算效率,而且会对后面的计算结果造成干扰.因此需要增加判断程序对这些不合理的解进行过滤.最后,对计算结果进行统计,取分布最集中的点作为取矩中心.
3) 计算对应工况下的安全系数
利用计算出来的滑裂面以及取矩中心,并结合瑞典条分法计算出下滑力矩MT.在计算MR1时通过导入到MATLAB中的UVARM用户自定义子程序计算出的有效法向应力场及土体状态参量,并结合滑裂面上的ci、φi值代入式(17)~(19)计算土体产生的抗滑力矩MR1.MR2、MR3分别为预应力锚索的极限抗拉承载力产生的抗滑力矩和支护结构底部的水平推力设计值产生的抗滑力矩,均可直接代入式(20)~(22)计算,不再赘述.
本文提出的滑裂面搜索模型及改进的安全系数计算模型与传统的极限平衡理论相比有三点区别:第一,滑裂面的搜索模型采用基于位移场的切向位移梯度法.第二,安全系数的计算模型考虑了浅层土体的张拉破坏对基坑抗滑力矩产生的不利影响.第三,抗滑力矩及下滑力矩的取矩中心的搜索模型引入理论力学中求解刚体瞬心的方法.
4 算例分析
4.1 工程概况
以兰州市某基坑为背景,基坑支护平面图如图7所示,基坑开挖深度为自然地面以下12.0~13.0 m,基坑底部绝对标高为1 522.217~1 523.217 m.本算例分析场地南侧排桩预应力锚索支护结构(即1-1剖面).场地南侧已建成28层住宅楼,取超载值为20 kPa.基坑安全等级为一级.
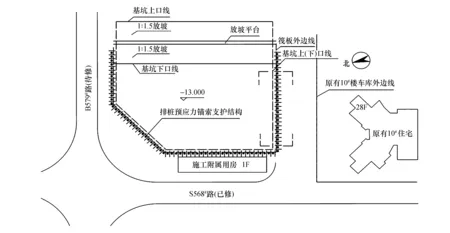
图7 基坑支护平面图(m)Fig.7 Foundation pit support plan(m)
土层信息如表1所示,支护结构的剖面图如图8所示.桩直径为0.8 m,桩间距为1.8 m.

图8 支护结构简图(m)Fig.8 Schematic diagram of the support structure(m)
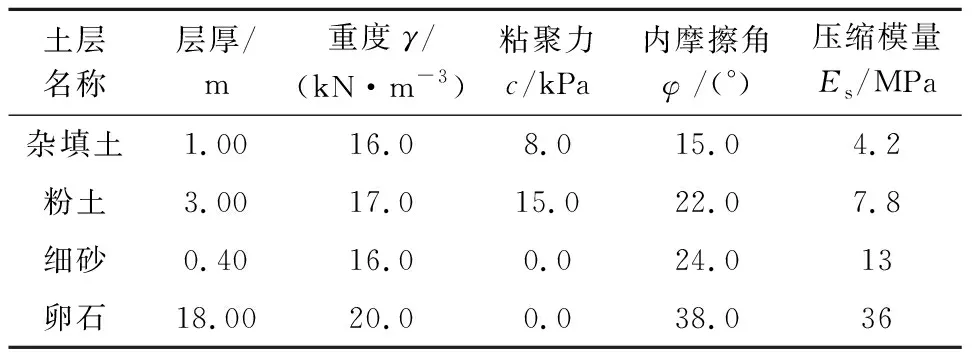
表1 土层信息Tab.1 Information of soil layers
锚索的布置形式如表2所示.在开挖至3.5 m深度时增设第一道锚索,锚索的埋深为3 m;在开挖至6.5 m深度时增设第二道锚索,锚索的埋深为6 m;在开挖至9.5 m深度时增设第三道锚索,锚索的埋深为9 m;最终开挖至13 m深度,到达基坑底部.

表2 锚索的布置形式Tab.2 Arrangement of anchor cable
4.2 有限元模拟及模拟结果分析
有限元模型及网格的划分情况如图9所示.通过UVARM用户自定义子程序可以计算出应力比云图(如图10所示).从图10中可以看出,滑动体区域附近的土体以及桩底附近的土体出现较大的应力比.同时,随着开挖的进行,应力比的数值在增大,等值面在向外扩张;随着锚索预应力的施加,应力比等值面在向内收缩,说明锚索预应力的施加可以减小桩后土体的应力比.

图9 有限元网格划分结果Fig.9 Results of finite element mesh
根据输出的应力比数据可以确定每一个施工步骤完成时墙后土体张拉破坏区的范围.式(17)计算土体抗滑力矩时,张拉破坏区土体的抗剪贡献将不予考虑.另外,从图10可以看出应力比在土层变化的位置会发生突变.
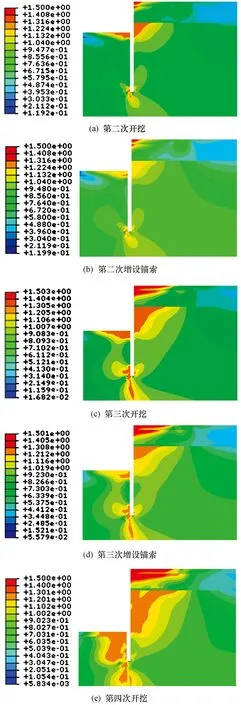
图10 应力比η云图Fig.10 Cloud map of stress ratio η
支护桩的侧向位移如图11所示,锚索拉力随施工步骤的变化情况如图12所示.从图11可以看出在四次开挖过程中桩顶的侧移量分别为向坑内侧移16.47 mm、8.11 mm、9.10 mm以及18.49 mm;在三次增设锚索过程中支护桩的侧移减小,桩顶的水平侧移量分别为向坑内侧移7.62mm、7.13mm以及10.85 mm.从图12可以看出先期施工的锚索的拉力值随着后期锚索预应力的施加而减小,锚索的拉力值均随着基坑的开挖而增加.

图11 桩身侧向位移曲线图Fig.11 Lateral displacement curve of pile body

图12 锚索拉力随施工步骤变化的关系曲线图Fig.12 Relationship between tension of anchor cable and construction steps
4.3 滑裂面搜索及取矩中心确定
将位移场数据、网格节点坐标、单元编号数据根据式(1)~(8)及式(23)~(27)编制相应的MATLAB程序即可获得滑裂面的形状.
图13为算例中滑裂面上某一点处切向位移梯度随切向方向的关系图.从图13可以发现滑裂面上点的切向位移梯度存在极大值.因此,切向位移梯度最大的方向可以反映滑裂面的切线方向.
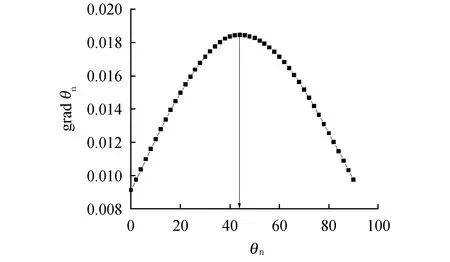
图13 切向位移梯度与方向角的关系Fig.13 Relationship between tangential displacement gradient and direction angle
滑裂面搜索结果如图14所示.对比滑裂面的位置以及应力比云图可以发现浅层土体应力比的降低会引起滑裂面向深层土体转移.
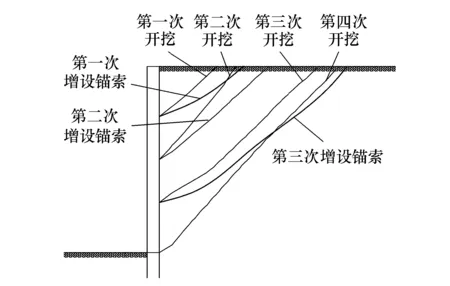
图14 滑裂面搜索结果示意图Fig.14 Schematic diagram of sliding surface
取矩中心的搜索过程分为两步:首先将滑裂面上所有节点排列组合,并代入式(12)和式(13)中计算“瞬心”;然后采用网格搜索法搜索“瞬心”最集中的位置.
算例中计算出的取矩中心的位置(标记为红色)如图15所示.从图中可以看出“瞬心”集中在较小的范围内.
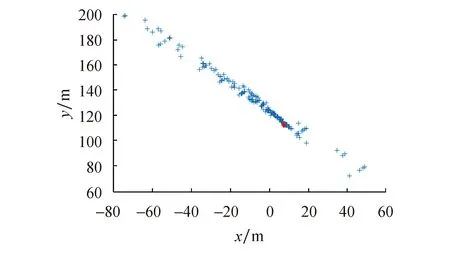
图15 瞬心点的空间分布以及搜索出的取矩中心的位置Fig.15 The spatial distribution of the instantaneous point and the location of calculation center of the moment
4.4 考虑张拉破坏的基坑动态稳定性分析
根据表1中的摩擦角计算出杂填土层及粉土层的M值分别为0.567和0.856.将M作为阈值在Abaqus中标记出张拉破坏区域.图16为用户自定义变量标记出来的第四次开挖结束时桩后土体的张拉破坏区域.

图16 通过UVARM标记出的张拉破坏区域Fig.16 Tensile damage zone marked by UVARM
通过对比前后施工步骤的张拉破坏区域可以看出,张拉破坏区随着基坑开挖向下延伸,并伴随着预应力的施加向上收缩.在应力比云图中也可以看出应力比较大的区域伴随着基坑开挖向下延伸,并伴随着预应力的施加向上收缩.这与实际情况符合,即在基坑开挖过程中桩后土体产生的张拉裂缝随着基坑的开挖发生扩展,并伴随预应力的施加发生闭合.因此,预应力的施加可以显著提高滑裂面附近土体的围压,提高滑裂面附近土体的抗剪强度,进而提高基坑在预应力施加后的动态稳定性.
将滑裂面上的节点坐标、取矩中心、张拉破坏区深度以及基坑的设计参数代入式(14)~(22)即可计算出基坑的安全系数,安全系数的计算结果如图17所示.从图中可以看出安全系数随着基坑的开挖而减小,随着锚索预应力的施加过程而增大.
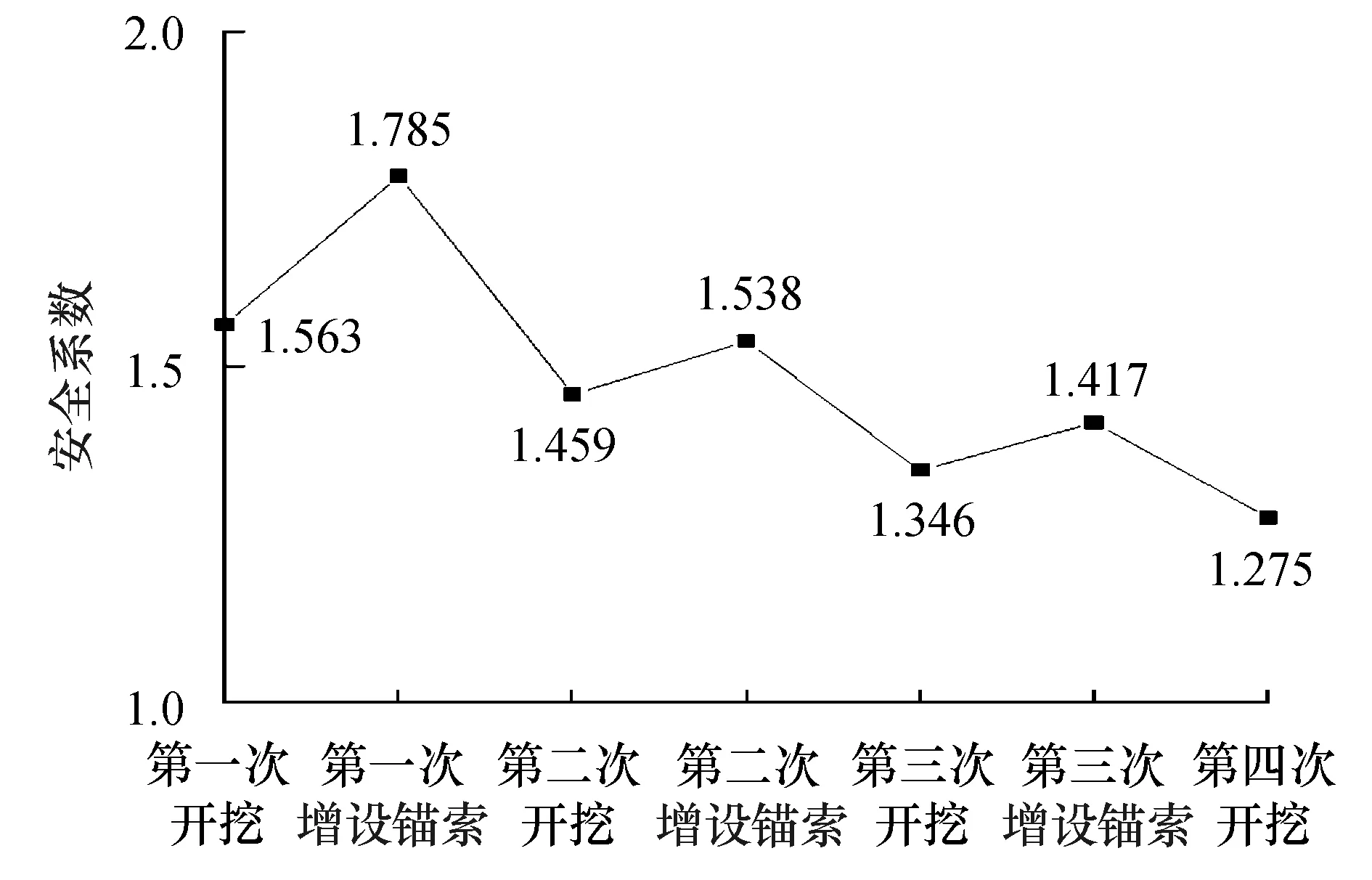
图17 安全系数随施工步骤的变化关系图Fig.17 Relationship between safety factor and construction steps
5 结论
1) 与传统滑裂面搜索模型相比,切向位移梯度法的假定较少,能够反映滑裂面的切线方向在土层变化位置处的突变情况.另外,切向位移梯度在0°~90°范围内存在极大值,符合实际情况.
2) 将应力比作为划分桩后土体的张拉破坏区以及剪切破坏区的判定条件,在进行安全系数计算时应对两种破坏区的土体采用不同的计算形式.
3) 本文计算出的张拉破坏区的土体位于浅层,说明浅层土因自重产生的围压较小,无法承担过大的剪应力而产生张拉裂缝.当剪切破坏区土体的极限抗剪承载力以及桩锚系统的极限抗拉承载力无法抵抗下滑力时,基坑将发生整体失稳破坏.
4) 对基坑支护方案进行施工全过程分析时发现:基坑的安全系数随着基坑的开挖而降低,随着锚索预应力的施加而提高,且预应力的施加可以改善墙后土体的应力比,使张拉破坏区收缩.
本文得到兰州理工大学红柳优秀青年项目的资助,在此表示感谢.
