单层吊顶地震反应分析的有限元计算模型

黄有露，蒋欢军，王勇

（1.同济大学土木工程防灾国家重点实验室，上海 200092；2.同济大学土木工程学院，上海 200092；3.中国建筑股份有限公司，北京 100037）

引言

吊顶具有良好的美观、保温和隔音性能，在建筑结构中应用广泛。然而，吊顶的抗震性能较差，在地震作用下容易发生节点破坏、面板掉落甚至大面积的垮塌现象［1－2］。例如，在2013年的四川芦山地震中，许多建筑中的吊顶面板发生掉落［3］。在2016年的意大利中部地震中，大量的吊顶节点发生破坏［4］。当地震发生时，吊顶的破坏不仅会造成经济损失和建筑使用功能的中断，甚至会引发人员伤亡。因此，研究吊顶在地震作用下的抗震性能对于提升建筑的安全性具有重要意义。

单层吊顶是一种不上人吊顶，其在国内外应用十分广泛。已有学者采取了足尺振动台试验揭示该类型吊顶的抗震性能，结果表明吊顶的边界条件、面积大小、地震动输入方向、面板的大小与重量、侧向支撑布置以及与其他设备之间的相互作用等因素均对其抗震性能具有影响［5－8］。然而，振动台试验费时费力，数值计算是一种研究吊顶抗震性能的更加便捷的方法。受限于吊顶中存在的复杂非线性行为，目前关于吊顶的有限元计算模型相对较少。

韩庆华等［9］基于ANASYS软件研究了吊顶的动力特性，并建议吊顶的阻尼比取2%～5%。王多智等［10］在ABAQUS软件中建立了一种能考虑吊顶接触碰撞的有限元模型，并指出主次龙骨节点会率先发生破坏并影响吊顶的整体性。然而，以上2种模型均未考虑龙骨连接点的非线性行为。已有研究表明，龙骨连接点在往复荷载作用下表现出明显的非线性特征。Zaghi等［11］使用OpenSees软件建立了能考虑节点非线性行为的吊顶三维有限元计算模型，但所研究的吊顶边界条件为两边固定两边自由型。相比于该类型的吊顶，自由型边界的吊顶在国内应用更多，其力学行为与两边固定两边自由型边界差异较大。冯云幸等［12］基于OpenSees软件提出了一种边界自由型吊顶的二维简化分析模型，并基于振动台试验结果验证了其有效性。目前，尚缺乏能够准确反映自由型吊顶地震反应的三维有限元计算模型。

为了便于采用数值分析的方法研究吊顶的抗震性能，文中提出了一种能够模拟四边自由型吊顶地震反应的三维有限元计算模型。该模型能够考虑吊顶龙骨连接点的非线性行为、面板与龙骨之间的摩擦和碰撞行为以及吊顶边界处的摩擦和碰撞行为。通过对该吊顶模型进行非线性时程分析并将有限元模拟结果与振动台试验结果进行对比，验证了该模型的正确性。

1 吊顶振动台试验

1.1 试件设计

吊顶试件根据JGJ 345－2014《公共建筑吊顶工程技术规程》［13］进行设计，为实际工程中常用的吊顶类型，试件照片如图1（a）所示。吊顶系统主要由龙骨体系（主龙骨、次龙骨、横撑龙骨和边龙骨）、吊杆以及面板组成，如图1（b）所示。次龙骨沿着X向布置，布置间距为600 mm。主龙骨与横撑龙骨沿着Y向间隔布置，布置间距为1 200 mm。边龙骨固定在吊顶的四周，其余龙骨构件的端部搁置在边龙骨上。吊顶共包含3种龙骨连接点类型，分别为主龙骨拼接点（2根主龙骨之间的连接点）、主次龙骨节点（主龙骨与次龙骨之间的连接点）和次横撑龙骨节点（次龙骨与横撑龙骨之间的连接点）。面板由矿棉板制成，厚度为16 mm，单块矿棉板的质量为1.2 kg。面板直接搁置在龙骨构件的翼缘上，与四周龙骨之间无任何连接措施。吊杆为8 mm的螺纹吊杆，长度为1 000 mm。吊杆的下端使用连接件与主龙骨相连，该连接件的上端通过螺栓与吊杆相连，下端通过螺钉固定在主龙骨上。整个吊顶系统通过吊杆锚固在钢框架（将在1.2节介绍）顶部的钢梁上。所有龙骨构件均由Q235钢材制成，屈服强度为235 MPa。龙骨构件的具体尺寸信息如表1所示。

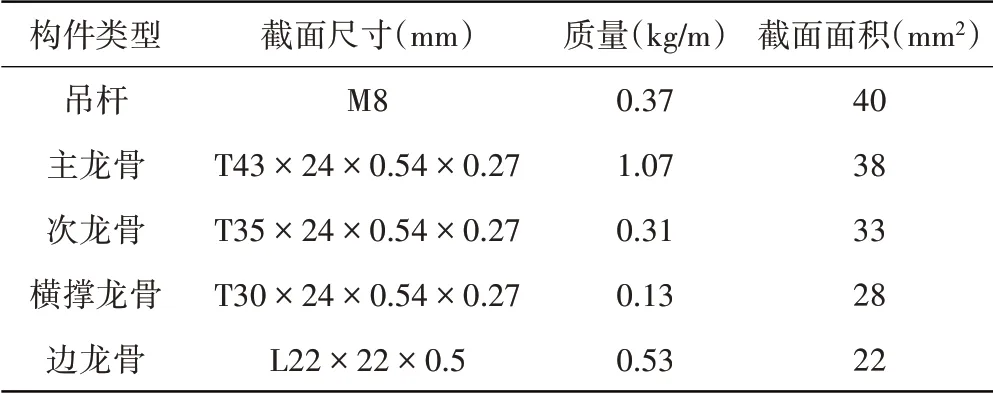
表1 龙骨构件详细信息Table 1 Details of grid components

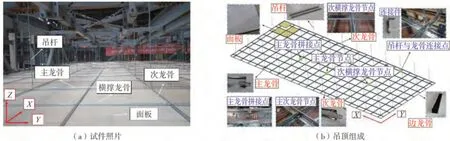
图1 吊顶示意图Fig.1 Schematic drawing of ceiling system

1.2 试验概况

本试验为吊顶足尺振动台试验，设计的钢框架如图2所示。吊顶的四边均为自由边，边龙骨固定在钢平台的周边梁上以支撑整个吊顶。为了记录该吊顶在试验过程中的动力响应，布置了加速度计、位移计和应变片，如图3所示。试验中共使用了3种输入，分别是正弦扫频波、人工波（来自于Building Center of Japan，命名为BCJ－L2［14］）以及建筑结构不同楼层处的加速度时程。其中，正弦扫频波的持时为100 s，频率范围为5～0.5 Hz或0.8 Hz。采用上海市DGJ08－9－2013《建筑抗震设计规程》［15］提供的地震波SHW6分别对一栋128层和一栋30层的建筑结构模型进行时程分析，并提取不同楼层处的加速度时程作为振动台试验的输入。在数值分析中，采用钢平台顶部的加速度时程作为输入。振动台试验的工况信息如表2所示，不同输入相对应的加速度反应谱（峰值加速度为1.0 g）如图4所示。

图2 试验钢框架Fig.2 Steel frame of the test

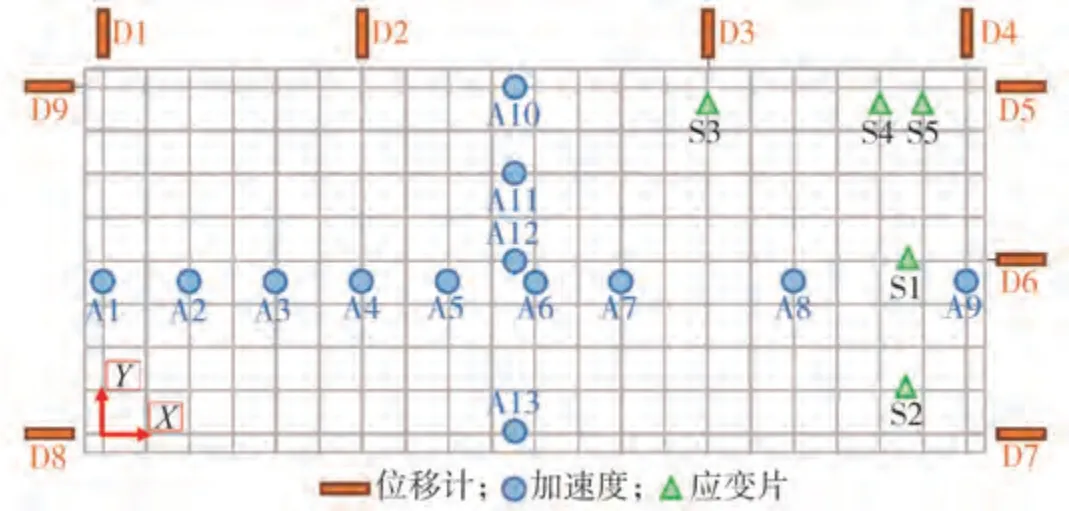
图3 测点布置Fig.3 Instrumentation arrangement

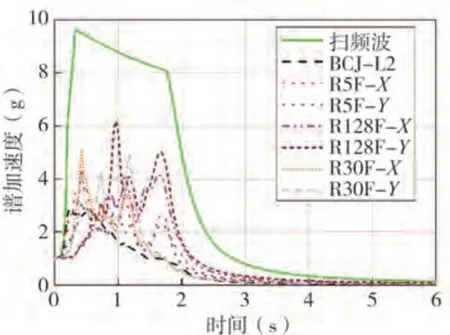
图4 输入波的加速度反应谱（阻尼比为5%）Fig.4 Acceleration response spectrum of input motions（with damping ratio of 5%）

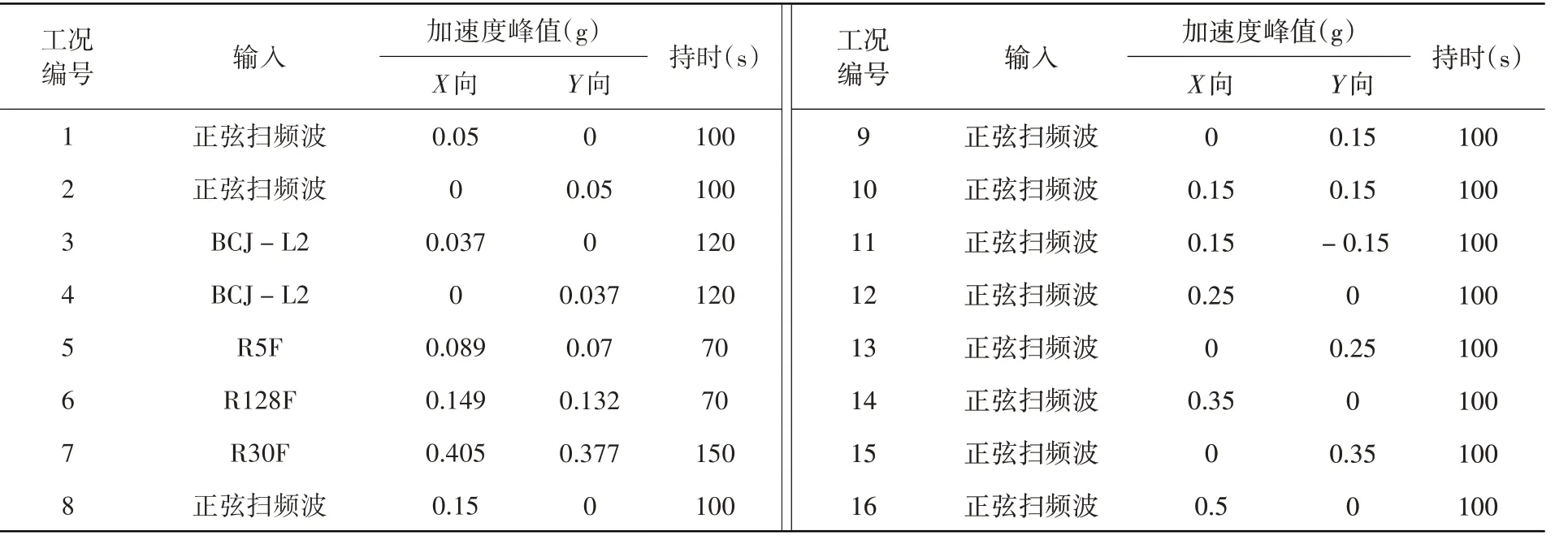
表2 试验输入Table 2 Test inputs

2 有限元计算模型

采用有限元软件OpenSees建立吊顶的三维有限元分析模型，模型示意图如图5所示。已有试验结果表明，主龙骨、次龙骨、横撑龙骨构件以及吊杆在地震作用下基本保持弹性状态，在模型中均采用elastic Beam⁃Column单元进行模拟［5］。吊杆的上端在模拟时简化为固结，下端与主龙骨的连接处根据其变形特征假定为刚接［16］。龙骨构件的质量简化为点质量布置在杆件的两端。钢材的弹性模量取206 GPa。吊顶的阻尼按照瑞利阻尼进行计算，阻尼比取5%［9］。

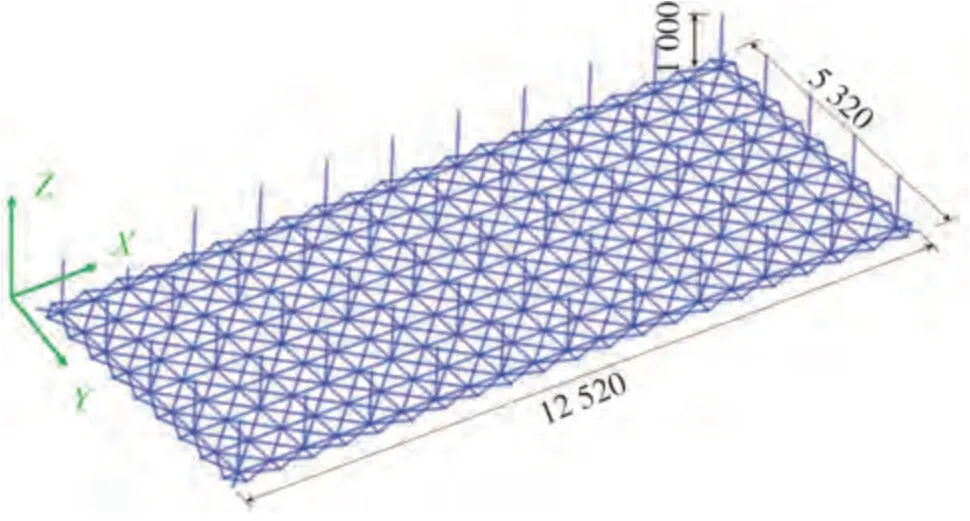
图5 吊顶三维有限元模型（单位：mm）Fig.5 Three-dimensional finite element model of suspended ceiling（Unit：mm）

2.1 龙骨连接点

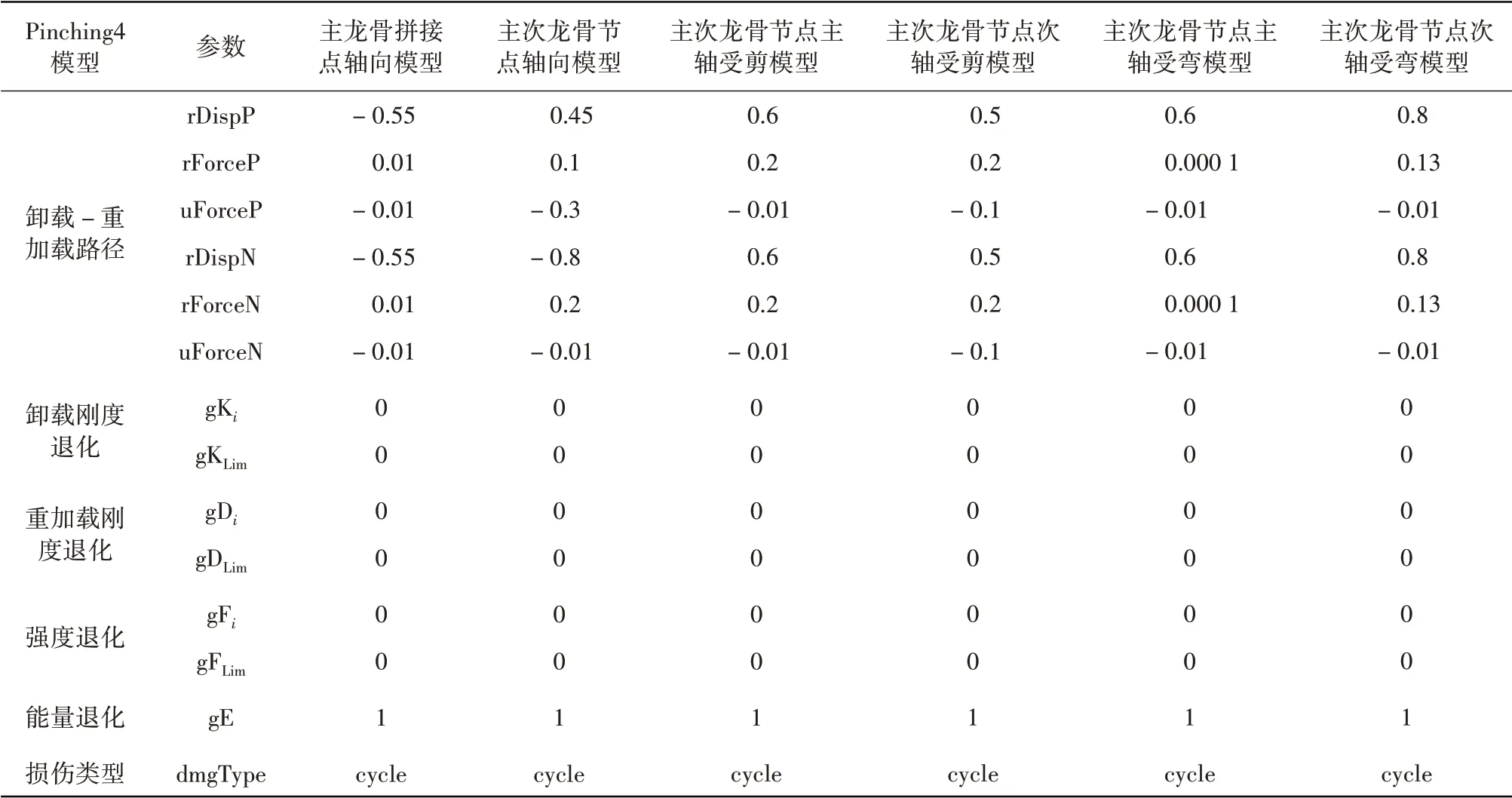
蒋欢军等［17］完成的构件试验结果显示，龙骨连接点在往复荷载作用下表现出明显的非线性特征。因此，在吊顶整体有限元计算模型中，使用ZeroLength单元模拟龙骨节点和拼接点，并采用Pinching 4材料模型定义龙骨节点和拼接点的轴向荷载－位移恢复力模型［18］。该材料模型共由39个参数控制，可以考虑在往复荷载作用下连接点的强度退化、刚度退化和捏拢效应，其荷载－位移关系曲线如图6所示。对于主次龙骨节点，在其剪切和受弯方向上同样采用Pinching 4材料模型定义相应的荷载－位移恢复力模型［19］。由于次横撑龙骨节点与主次龙骨节点的构造基本一致，因此2种节点使用相同的模型参数。在有限元计算模型中，Pinching 4模型的具体参数取值如表3所示。

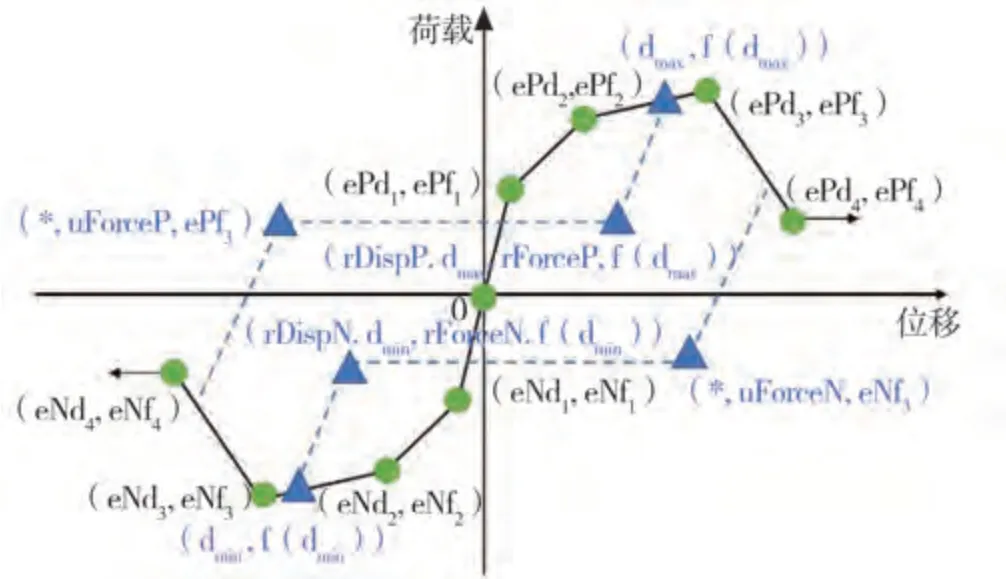
图6 Pinching 4模型Fig.6 Pinching 4 model

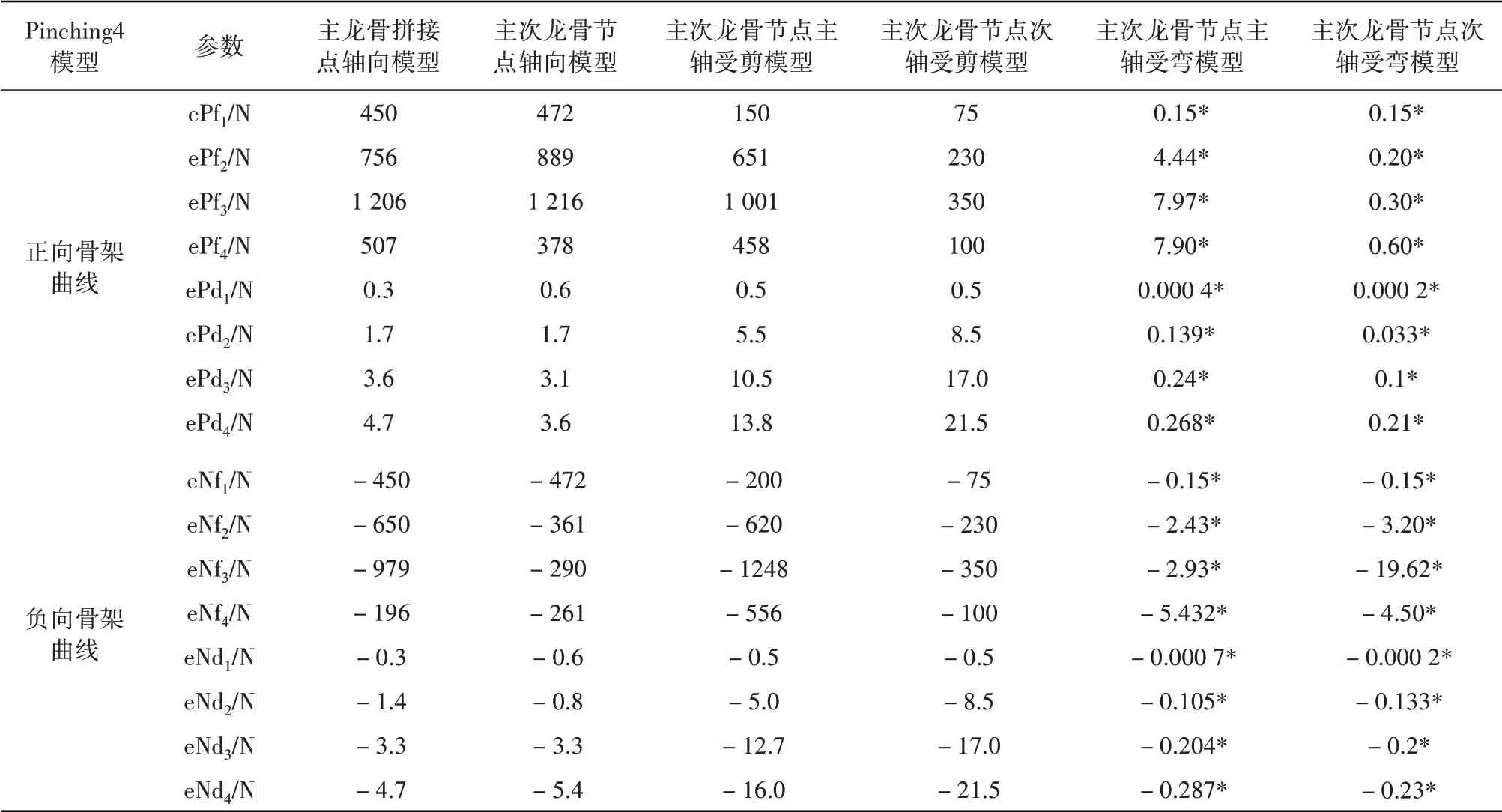
表3 Pinching 4模型的参数取值Table 3 Parameter values of Pinching 4 model

续表

2.2 面板与龙骨的相互作用

面板的面内刚度较大，在地震作用下基本保持弹性状态，图7给出了面板的建模方法。面板由一个中心点（占1/2面板质量）和4个角点（占1/8面板质量）以及连接面板中心点和4个角点的twoNodeLink单元构成［11］。对该单元赋予Elastic材料，轴向刚度取为19 500 N/mm［12］。为了便于面板在工程现场的安装，面板与四周龙骨之间通常存在一定的间隙，平均间隙值为3 mm。该间隙的存在会导致面板在地震作用下与龙骨之间存在摩擦和碰撞行为。因此，采用2个ZeroLength单元连接面板的角点和与其相邻的龙骨连接点。对其中一个ZeroLength单元赋予ElasticPPGap材料模型以模拟面板与龙骨之间的碰撞行为（X和Y这2个方向），碰撞刚度取为10.9 N/mm［12］。对另一个ZeroLength单元赋予ElasticPP材料模型以模拟面板与龙骨之间的摩擦行为（X和Y两个方向），摩擦系数取为0.3［12］。

图7 面板建模方法Fig.7 Modeling method of panel

2.3 边界条件

对于四边自由型吊顶，龙骨构件的端部直接搁置在边龙骨上并存在一定的间隙，如图8所示。在地震作用下，龙骨的端部与边龙骨之间会存在摩擦和碰撞行为。对于碰撞行为，使用ZeroLength单元进行模拟，并在碰撞方向上定义ElasticPPGap材料模型。选取0.4倍的龙骨轴向线刚度作为碰撞刚度值［20］，计算得出主龙骨、次龙骨和横撑龙骨对应的碰撞刚度分别为588、217、433 N/mm。碰撞间隙的宽度值根据在振动台试验中（将在3.1节介绍）测得的位移大小进行确定。对于摩擦行为，使用ZeroLength单元并定义ElasticPP材料模型进行模拟。考虑龙骨端部在两个水平方向上的摩擦行为，摩擦力根据振动台试验结果进行标定，取为2 N。

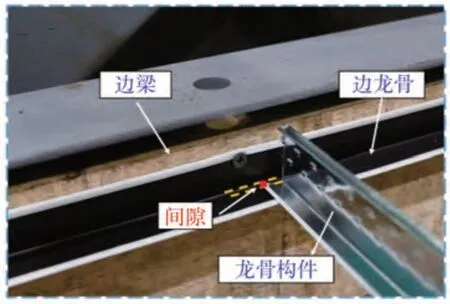
图8 自由边界条件Fig.8 Free boundary condition

3 有限元模拟与试验结果对比

根据振动台试验中的工况，对建立的吊顶模型进行非线性时程分析。在试验中，该吊顶在工况13之后部分龙骨从边龙骨上脱落，此时该模型不再适用，因此只模拟到该工况。将有限元模拟结果与试验结果进行对比，包括吊顶的加速度、位移以及龙骨轴力。

3.1 加速度

以工况7（楼面最大加速度时程）、工况8～10（单向和双向扫频波）为例，图9对比了试验和有限元模拟得到的吊顶在2个方向上的加速度时程和傅里叶谱。从图中可以看出，模拟得到的加速度时程的趋势与试验结果基本一致，但模拟得到的加速度峰值更大。产生该现象的原因是吊顶的加速度除了受到边界处碰撞行为的影响，还对面板与龙骨之间的碰撞行为比较敏感，合理的确定碰撞刚度大小是计算吊顶加速度的关键。进一步根据傅里叶谱的对比结果可以发现，模拟得到的加速度频谱与试验结果吻合较好，但模拟结果的高频成分居多。整体而言，所提出的有限元模型能够用于计算吊顶的加速度反应。

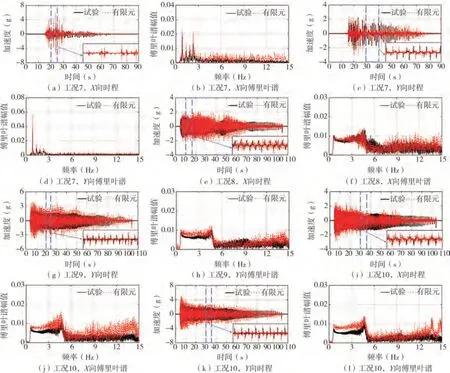
图9 模拟与试验加速度结果对比Fig.9 Comparison of acceleration between numerical simulation and experimental results

3.2 位移

同样以工况7～10为例，图10对比了有限元模拟和试验得到的吊顶在2个方向上的位移时程和傅里叶谱。从图中可以看出，模拟得到的位移结果在时域和频率范围内与试验结果均吻合良好。在不同工况下的位移峰值的对比结果如表4所示。可以看出，在大多数工况下，有限元模拟和试验结果的误差控制在25%以内。然而，在部分工况尤其是输入加速度较小（工况1～4）的工况下误差很大。误差产生的原因有：一是与根据振动台试验采集的位移结果确定端部间隙宽度的方法有关（由于施工精度和试验条件限制，该方法难以真实反映实际的间隙宽度值）；二是与有限元模型中面板与龙骨之间的摩擦系数取值与实际结果存在一定差异有关（该系数有待通过相关的摩擦试验进行确定）。整体而言，所提出的有限元模型能够用于计算吊顶的位移反应。

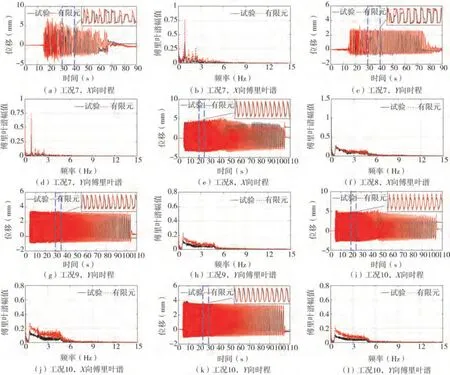
图10 模拟与试验位移结果对比Fig.10 Comparison of displacement between numerical simulation and experimental results

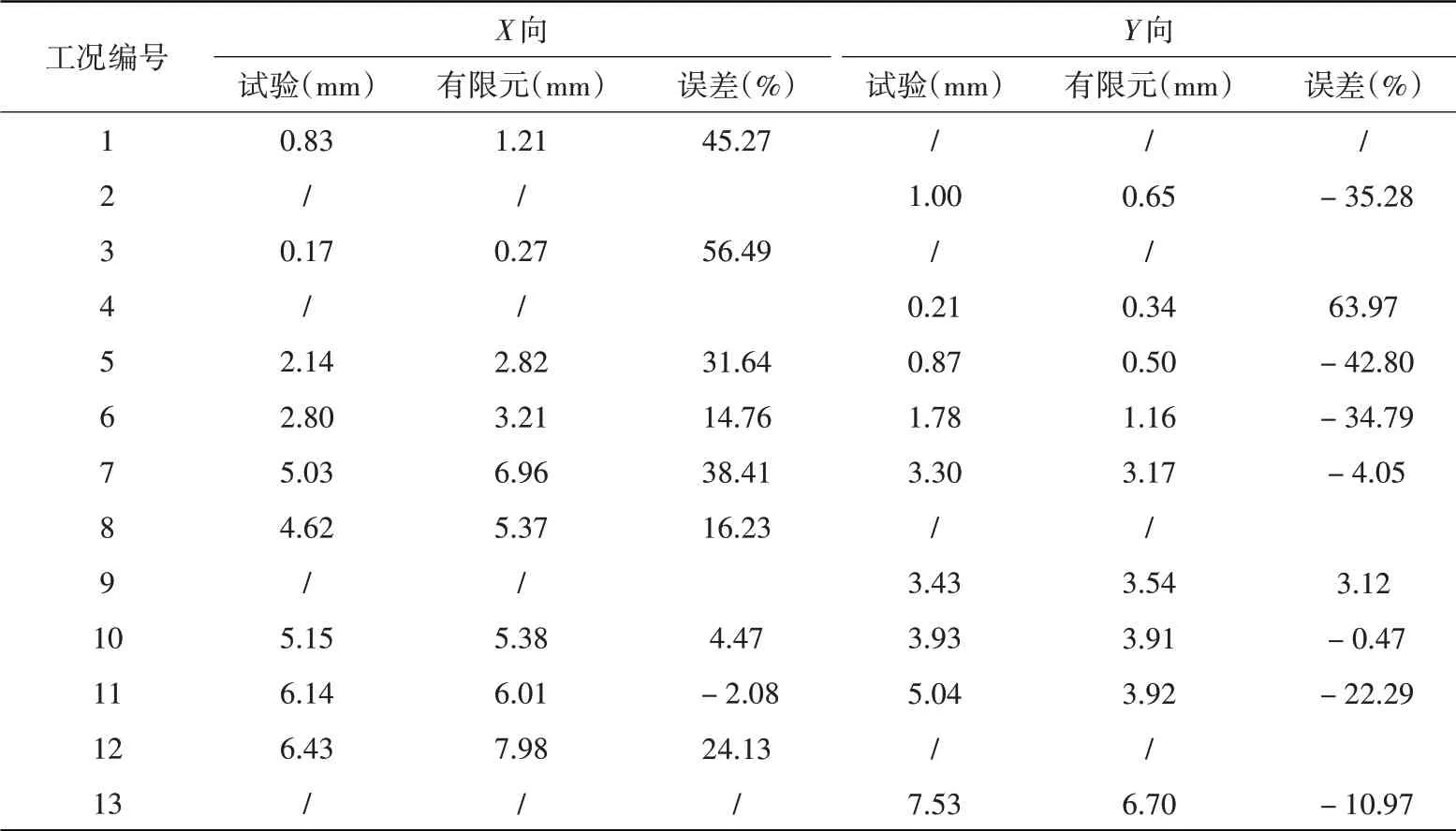
表4 峰值位移对比Table 4 Comparison of peak displacements

3.3 龙骨轴力

龙骨连接点破坏是吊顶破坏的重要特征，而龙骨轴力的大小是引起吊顶连接点破坏的重要原因。在振动台试验中，主龙骨、次龙骨和横撑龙骨上均布置了应变片（如图3所示），相应龙骨的轴力大小可根据胡克定律和构件截面面积进行计算。图11给出了在不同工况下有限元模拟得到的龙骨轴力与试验结果的对比。从图中可以看出，随着地震动强度的增大（工况3～7），龙骨轴力随之增大。对于横撑龙骨构件，其在工况3～7下有限元模拟得到的龙骨轴力与试验结果误差较大。在振动台试验中受限于位移计的数量，横撑龙骨的端部未布置位移计，因此在有限元分析中该间隙值假定与同侧的主龙骨端部间隙值相同，该简化会导致分析得到的横撑龙骨的轴力与试验结果存在差异。在大多数工况下，模拟得到的龙骨轴力大小与试验结果吻合良好。

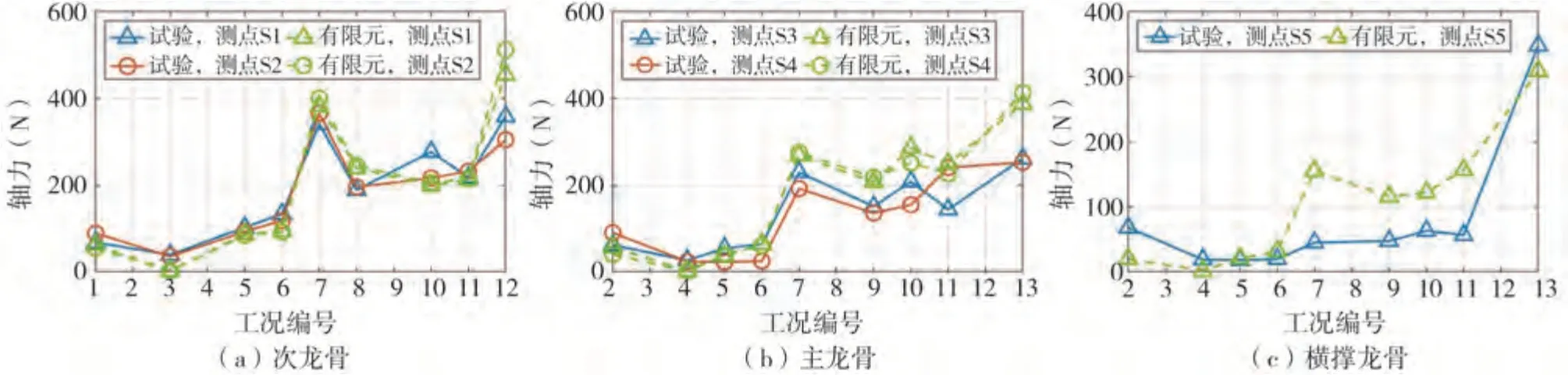
图11 模拟与试验龙骨轴力结果对比Fig.11 Comparison of grid axial force between numerical simulation and experimental results

4 结论

文中介绍了一种可模拟单层吊顶地震反应的三维有限元计算模型，该模型能够考虑龙骨连接点的非线性行为、面板与龙骨之间以及吊顶边界处的摩擦和碰撞行为。通过对该有限元计算模型进行非线性时程分析，得到的结论如下：

（1）模拟得到的加速度中高频成分居多，且加速度峰值对吊顶中存在的碰撞行为较为敏感。在大多数工况下，模拟得到的位移峰值与试验结果的误差控制在25%以内。模拟得到的龙骨轴力与试验结果基本吻合。

（2）对于边界自由型的单层吊顶，吊顶中存在的摩擦行为和碰撞行为对其动力响应影响显著。合理地确定分析参数的取值对于准确计算吊顶的加速度、位移和龙骨轴力大小至关重要。

（3）通过将模拟得到的加速度、位移和龙骨轴力与试验结果进行对比，验证了有限元计算模型的正确性。文中所提出的吊顶有限元模型为吊顶的抗震性能分析与设计提供了有效的分析工具。

受模拟地震振动台设备加载条件限制，本试验只输入了水平方向的地震动，未输入竖向地震动。由于文中的主要工作是提出吊顶的有限元计算模型并用振动台试验结果对计算模型进行验证，因此暂未考虑竖向地震动的影响。已有的研究结果表明，竖向地震动对吊顶的抗震性能有较显著的影响，过大的竖向加速度会引起矿棉板相对龙骨构件发生跃起行为，并进一步导致面板发生错位或掉落现象。在后续的研究中，将进一步分析竖向地震动对吊顶抗震性能的影响。