A novel stacking-based ensemble learning model for drilling efficiency prediction in earth-rock excavation

Fei LV, Jia YU, Jun ZHANG, Peng YU, Da-wei TONG, Bin-ping WU

Research Article

A novel stacking-based ensemble learning model for drilling efficiency prediction in earth-rock excavation

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300350, China

Accurate prediction of drilling efficiency is critical for developing the earth-rock excavation schedule. The single machine learning (ML) prediction models usually suffer from problems including parameter sensitivity and overfitting. In addition, the influence of environmental and operational factors is often ignored. In response, a novel stacking-based ensemble learning method taking into account the combined effects of those factors is proposed. Through multiple comparison tests, four models, eXtreme gradient boosting (XGBoost), random forest (RF), back propagation neural network (BPNN) as the base learners, and support vector regression (SVR) as the meta-learner, are selected for stacking. Furthermore, an improved cuckoo search optimization (ICSO) algorithm is developed for hyper-parameter optimization of the ensemble model. The application to a real-world project demonstrates that the proposed method outperforms the popular single ML method XGBoost and the ensemble model optimized by particle swarm optimization (PSO), with 16.43% and 4.88% improvements of mean absolute percentage error (MAPE), respectively.

Drilling efficiency; Prediction; Earth-rock excavation; Stacking-based ensemble learning; Improved cuckoo search optimization (ICSO) algorithm; Comprehensive effects of various factors; Hyper-parameter optimization

1 Introduction

Earth-rock excavation, consisting of four main operations: drilling, blasting, loading, and hauling, plays a pivotal role in the entire schedule of earthworks (Abu Bakar et al., 2018; Li, 2018; Wang and Wu, 2019). Undoubtedly, drilling is considered as the foundation, appropriate design of which will bring about a more compatible blasting, loading, and hauling operation (Abbaspour et al., 2018). Drilling efficiency may affect the schedule of blasting operations, thus affecting the excavation progress of the whole quarry. A faster drilling efficiency can advance the blasting schedule of excavated blocks, so greatly advancing the progress of excavation. Accurate prediction of drilling efficiency can contribute to the calculation of the excavation period and play an important guiding role in developing and adjusting the subsequent schedule in a timely way (Kahraman et al., 2003). In addition, as the quarry is in the open air, the drilling efficiency may change continuously owing to various influencing factors such as rock properties, machines, staffing, and weather (Darbor et al., 2019). It is of vital importance to comprehensively consider multiple factors for drilling efficiency prediction in earthwork excavation. Therefore, a novel drilling efficiency prediction method is needed for earth-rock excavation which considers many factors that affect it.

Researchers have carried out studies on the prediction of drilling efficiency. Some of them predicted drilling efficiency by establishing mathematical models (Kahraman, 2002; Akün and Karpuz, 2005; Saeidi et al., 2014; Abbaspour et al., 2018). These models carried out multiple regression analysis with the effects of some auxiliary data, such as bit properties, bit diameter, mud properties, and revolutions per minute (r/min). However, these mathematical models cannot comprehensively and accurately estimate the drilling efficiency because of the highly nonlinear and complex relationship between the drilling parameters and drilling efficiency (Abbas et al., 2019). Furthermore, these models did not consider the influence of operational and environmental factors quantitatively. These drawbacks have triggered the development of machine learning (ML) methods, which are an attractive alternative for describing and modelling the complicated process (Elkatatny, 2018; Abbas et al., 2019). The most representative characteristic of ML is its ability to build a complex model and to provide intuitive solutions through a typical learning process without formal description of the underlying physics (Paul et al., 2018; Abbas et al., 2019). Many existing studies employ popular ML methods, such as neural networks and regression models (Shi et al., 2016; Darbor et al., 2019; Koopialipoor et al., 2019). However, these single models also suffer from some inherent shortcomings, such as the sensitivity of parameters, local optimum, and overfitting (Cui et al., 2021).

Many researchers have, therefore, focused on improving the stability and generalization performance of single ML models through regularization, parameter optimization, and other new technologies. Ensemble learning methods have emerged that can further improve prediction accuracy and overcome the shortcomings of single ML models (Chen et al., 2018). With their improvement of predictive power, ensemble learning methods have attracted widespread attention within the computational intelligence community and have shown outstanding performance in many practical applications (Pernía-Espinoza et al., 2018; Guo et al., 2020; Cui et al., 2021; Cankurt and Subasi, 2022). The core idea of ensemble learning is to aggregate the advantages of several different models and build a relatively powerful model to improve performance (Chen et al., 2018; Li et al., 2019; Wang et al., 2020; Kaushik et al., 2022). The mechanism by which ensemble learning improves performance is usually to reduce the variance component of the prediction error caused by the contribution models. The average prediction performance can be improved by the ensemble over any contributing member. A variety of ensemble learning models have been widely applied to prediction problems in the field of civil engineering and one of these is geological prediction (Chen et al., 2021; Haghighi and Omranpour, 2021; Yan et al., 2022).

When building drilling efficiency prediction models, most of the existing studies have failed to use optimization methods to select multiple parameters, and have thus ignored the significant influence of parameter selection on model performance. Recently, some swarm intelligence algorithms have shown good performance in parameter optimization with the advantage of quickly finding a global approximate optimal solution and solving complex nonlinearity problems such as combinatorial optimization (Bui et al., 2018; Qi et al., 2018; Ren et al., 2020; Cui et al., 2021). Based on a comprehensive comparison of other swarm intelligence optimization algorithms, the cuckoo search optimization (CSO) algorithm is selected here to optimize the hyper-parameters of the ensemble learning model.

Existing studies developed to predict drilling efficiency mainly focus on geological factors and the influence of drilling machine characteristics. Nevertheless, operational and environmental factors may also influence drilling performance dynamically and simultaneously (Darbor et al., 2019). This paper mainly focuses on the efficiency of drilling operations in earthwork excavation. The excavated quarry provides filling materials for a hydraulic project; it is in the open air and many boreholes need to be drilled. Compared with the depth drilled per unit time, we pay more attention to the drilling duration of each borehole under different conditions to make the follow-up schedule timely and convenient, and to provide a basis for subsequent research. Thus, in this study, the drilling efficiency is defined as the time required for drilling each borehole (h/hole). The quantitative influence of operational and environmental factors on drilling efficiency prediction should not be underestimated. For example, the weather (sunny or cloudy) will affect the lighting, thus affecting the assembly of the drilling machines, and different numbers of operators can significantly influence the duration of adding or unloading drill pipes, and so influence drilling efficiency. Therefore, it is necessary to develop a comprehensive prediction model for drilling efficiency in earthwork excavation that takes the above factors into consideration.

Based on these discussions, a novel stacking-based ensemble learning model is proposed for drilling efficiency prediction in earthwork excavation. The extensive experimental results with different combinations of varying types and numbers of base learners demonstrate that the model achieved the best prediction performance when eXtreme gradient boosting (XGBoost), random forest (RF), and back propagation neural network (BPNN) were used as the base learners, and support vector regression (SVR) was used as the meta-learner. A major advantage of the proposed ensemble method is the enhancement of the fitting ability of the individual models and the handling of regression prediction with limited data more accurately by the integration of multiple single ML methods.

The main components of this study may be summarized as follows:

1. The comprehensive effects of various factors including geology, operation, environment, and machine characteristics are considered quantitatively in the drilling efficiency prediction model of earthwork excavation.

2. An ensemble learning model, integrating four different models, XGBoost, RF, BPNN, and SVR, is proposed to generate a combined model for predicting the drilling efficiency in earthwork excavation.

3. To optimize the key parameters and further improve the accuracy of the ensemble learning model, an improved cuckoo search optimization (ICSO) method with an adaptive step-size strategy is proposed.

2 Related works

To estimate drilling efficiency, a few studies describe mathematical models designed to explore the correlation between drilling parameters and drilling efficiency. For example, Kahraman (2002), by summarizing the raw data from other researchers' experimental work, found the correlation of rock brittleness and the performance of drilling machines in rock excavation. Akün and Karpuz (2005) derived an empirical correlation to predict the drilling rates of a surface set diamond bit for sandstone. Abbaspour et al. (2018) adopted, for subsequent optimization of drilling and blasting operations, the equation presented by Hustrulid et al. (2013) for predicting the penetration rate in a drilling operation. These studies usually considered "average" rock properties. To consider the influence of the uncertainty of rock properties, Saeidi et al. (2014) developed a non-linear multiple regression prediction stochastic model using a Monte Carlo method, for the penetration rate of rotary drills. Mustafa et al. (2021) developed a mathematical relation between drilling speed and operational controllable drilling parameters.

With the development of ML technology, some researchers have tried to use ML methods (Abbas et al., 2019). Darbor et al. (2019) used a multilayer perceptron-artificial neural networks (ANNs) model to assess the rate of penetration (ROP) of a rotary drilling machine and their results indicated that the neural network is an effective tool for reducing the uncertainties of the drilling operation. Gan et al. (2019) introduced a wavelet filtering method to reduce noise in the drilling data and then proposed a hybrid bat algorithm optimized SVR to predict the ROP. Salimi et al. (2016) employed an adaptive neuro-fuzzy inference system together with SVR for the performance prediction of hard rock tunnel boring machines (TBMs). Considering the 19 highest impact variables, Abbas et al. (2019) used ANNs to predict the ROP and to estimate the drilling time of deviated wells. Koopialipoor et al. (2019) developed a deep neural networks (DNNs) model for predicting the penetration rate of the TBM and compared the model with ANNs. Shi et al. (2016) used the typical extreme learning machine (ELM) and upper-layer solution-aware (USA) for ROP prediction, and the simulation results showed that the proposed model outperforms the ANNs model. It can be seen that, compared with mathematical models, ML models are more flexible, have higher prediction accuracy and take more factors into account.

Although ML models overcome some shortcomings of mathematical models, there are still some limitations of the single ML model. When handling complex process data, even the most powerful ANNs model still cannot obtain the expected performance (Zhang et al., 2018). As a frontier technology in the field of ML, the ensemble learning model can overcome some of the shortcomings of single ML models (Chen et al., 2018). Increasingly, studies have confirmed that ensemble learning models can outperform single models and achieve better results for the same problems, because there are complementary strategies among some single ML models (Li et al., 2018; Zhang et al., 2018; Wang et al., 2021). For example, Wang et al. (2020) used ensemble learning to present a probabilistic approach to forecasting wind gusts and quantifying uncertainty in the prediction of wind gusts, including three ML models: RF, long short-term memory, and Gaussian process regression. Chen et al. (2021) designed a multioutput ensemble learning framework integrating the ELM and SVR to capture the complex mapping from environmental factors to deformation and to provide more reliable forecasts of dam deformation. In summary, by integrating various single ML models, the ensemble learning model often demonstrates better prediction performance and ability.

There are three typical integration strategies: bagging (the parallel method), boosting (the sequential method), and stacking (Galar et al., 2012). Based on the characteristics of base models, ensemble learning can also be divided into two categories (Mendes-Moreira et al., 2012). If different algorithms are integrated for the ensemble, the model is defined as heterogeneous; otherwise it is defined as homogeneous. Theoretically, bagging and boosting strategies generally integrate homogeneous base models, whereas stacking can integrate heterogeneous models. Compared with bagging and boosting, stacking strategy can combine the outputs predicted by multiple base learners as the input (training data) for a meta learner to approximate the same target function (Pernía-Espinoza et al., 2018). This enables original data sets and the prediction results of base learners to be effectively deployed, which reduces the deviation and improves the prediction accuracy (Cui et al., 2021). The high diversity between the predictions of base models encourages improvement. To further clarify the reliability and functionality of the stacking model, Cui et al. (2021) proposed an illustrative case. The results not only showed that the diversity of base learners can improve the generalization ability of the model, but also proved that the cross-validation method used in the training of base learners can further improve the robustness of the model. Certainly, the stacking model has already been successfully applied in many fields. For example, Yan et al. (2022) presented a stacking classification algorithm to predict geological characteristics and the results showed the superiority of the proposed method. Haghighi and Omranpour (2021) applied a stacking ensemble model to Persian/Arabic handwriting recognition that improved the recognition performance for challenging handwritten texts. Therefore, to better take advantage of the performance of various models, we adopt a stacking strategy that can combine a variety of heterogeneous models for prediction of drilling efficiency.

3 Framework

In this section, we describe the proposed drilling efficiency prediction method considering the quantitative influence of synthetic effect factors. To verify the effectiveness of the model, a total of 155 sets of data on drilling efficiency and the corresponding effect factors for earth-rock excavation were collected. The overall framework comprises three steps as illustrated in Fig. 1.

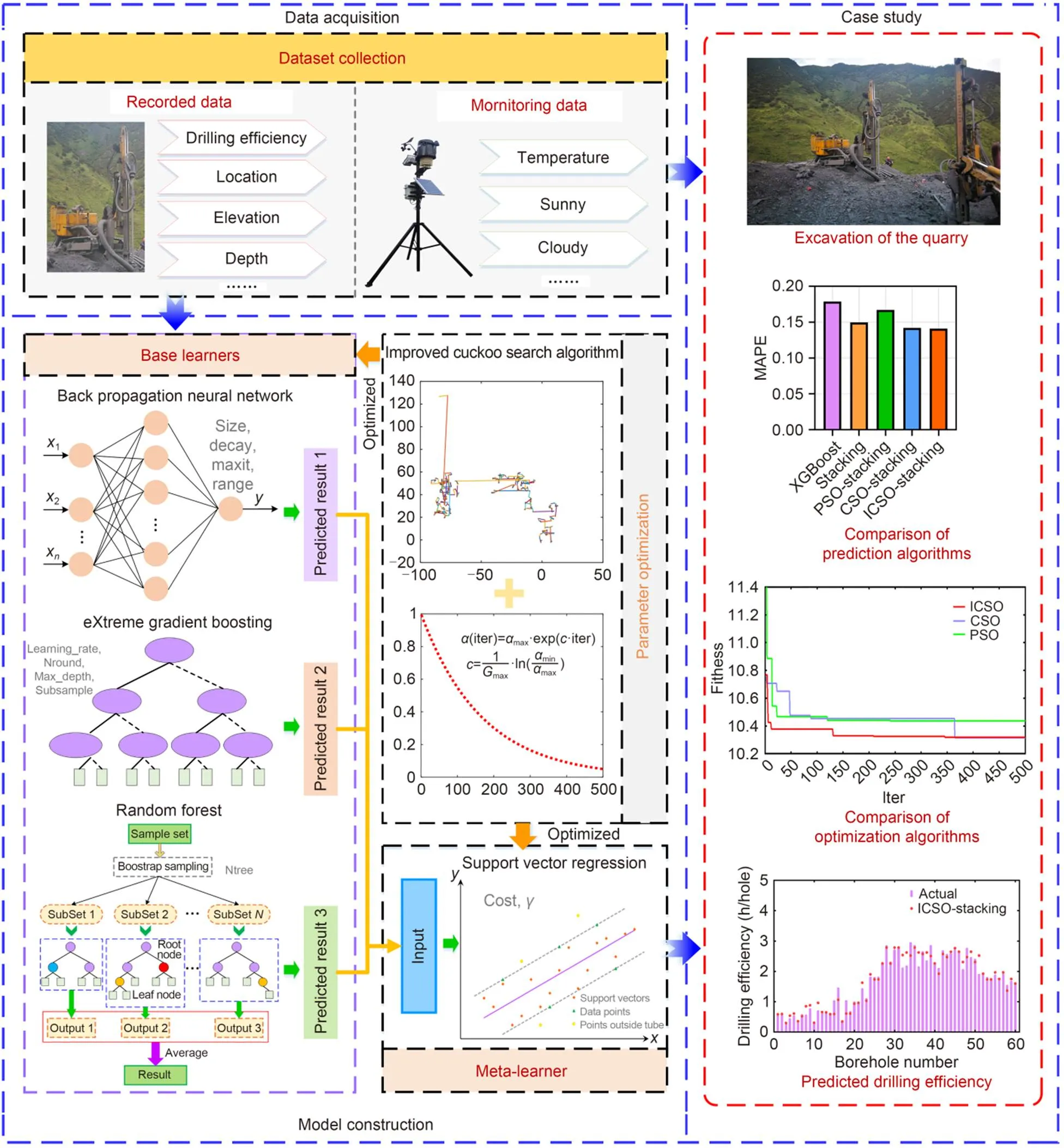
Fig. 1 Framework of the proposed method. Explanations of the parameters are given in the following sections

1. Data acquisition and pre-processing

The data of drilling efficiency and relevant effecting factors were collected. The factors determined from all four aspects, geology, operation, environment, and machine characteristics, were such as depth of the borehole, weather, staffing, and type of rock. Section 4.1 will describe the detailed process.

2. Model construction

There were three important aspects. The first was the base learner layer modelling of the stacking-based ensemble learning. After multiple attempts and experiments, three heterogeneous models, XGBoost, RF, and BPNN, were selected as the base learners. The sample data of drilling efficiency and related effect factors were input into each base learner. The second aspect is meta-learner modelling. SVR was proposed as the meta-learner by multiple experiments. The drilling efficiency prediction results of these three base learners were integrated as input to the meta-learner for further improving the accuracy of the model. Finally, the third aspect was parameter optimization based on ICSO. The ICSO with an adaptive step strategy was developed to optimize sensitive parameters such as Max_depth of XGBoost and the number of trees of RF in the stacking-based ensemble learning model.

3. Case study and model evaluation

A real-life case of an earthwork under construction in southwest China was implemented to verify the presented approach. The robustness of the proposed model was proved by applying the fivefold cross-validation method. Five common evaluation indexes, mean square error (MSE), root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and-squared (2) were used to evaluate the model's accuracy and generalization performance.

4 Methodology

In this section, an enhanced stacking ensemble learning model optimized by ICSO for drilling efficiency prediction is introduced. The ensemble model takes advantage of XGBoost, RF, BPNN, and SVR, which are practical techniques for working with a limited number of input samples and dominating the local optimal solution problem (Kazemzadeh et al., 2020; Cui et al., 2021), and thus exhibits better prediction performance.

4.1 Data acquisition and preprocessing

A dataset of drilling efficiency and corresponding influencing factors was collected in this study. Before collecting data, we went to the construction site for investigation for at least three months. Through field investigation, pre-analysis, interviews with several experienced engineers, and analysis of measured data, we finally selected ten features as influencing factors for drilling efficiency. Firstly, we recorded the essential information, including year, month, day, and the beginning and end times of the drilling process of each drill hole. The quantity and time for adding and unloading the drill pipes per borehole were also recorded. The coordinates, elevations, and depth of boreholes as well as the type of rock and drilling machines were recorded at the same time. Secondly, the meteorological monitoring station automatically recorded a set of meteorological data every 10 min, and the weather conditions corresponding to each borehole were extracted. Finally, these different features were combined and there were ten features that affected the drilling, as shown in Table 1.

Based on the beginning and end times of the drilling process of each borehole, we calculated the time required for drilling each borehole, which is the drilling efficiency to be analyzed and predicted in this study. The 10 influencing factors were from four areas, geology, operation, environment, and machine characteristics, such as elevation, depth of the borehole, weather, staffing, and type of rock. Among these factors, the elevation refers to the altitude of the working face, the changes of which may affect air pressure, machine performance, and personnel status. In regard to the depth of the borehole, the pressure of the machine will change as the depth changes, thus changing the drilling efficiency. Different temperatures and rock types may directly affect the efficiency of the drilling machine. Different types of machines vary in performance and efficiency. For outdoor operation, the weather (sunny or cloudy) will affect the lighting, thus affecting the assembly and operation of the drilling machines. According to the construction operation manual, each drilling machine should have at least one operator for operation. In fact, adding auxiliary personnel to the original personnel can significantly reduce the time needed to add or unload drill pipes, thus improving drilling efficiency.

However, the dataset is not in a standard format that can be used directly as an input to the model. Therefore, we normalized the dataset. For discrete features, zero and one are used to label different classifications of each feature. For example, there are four types of machines used for drilling, namely Atlas Copco T40 (Jiangsu En Vale Trade Co., Ltd., China), Innovake DR55B (Innovake Rock Drilling Machinery Co., Ltd., China), Crawler Hydraulic Drill JK590 (Zhangjiakou Xuanhua Jinke Drilling Machinery Co., Ltd., China), and Xuanhua Hydraulic Crawler Drill (Zhangjiakou Xuanhua Jinke Drilling Machinery Co., Ltd., China). Different types of drilling rigs have different drilling efficiencies. However, this is an unordered classification variable, which needs to be converted into dummy variables before it can be put into the model. Therefore, (0, 0), (0, 1), (1, 1), and (1, 0) represent different types of machines in this study.

4.2 Stacking-based ensemble learning

Stacking-based ensemble learning aggregates the advantages of the base learners and the meta-learner through two-layer integration to improve the accuracy and robustness of the model and to reduce the generalization error (Pernía-Espinoza et al., 2018). The base learner layer consists of a variety of heterogeneous learners. The sample data of drilling efficiency and related effect factors are input into each base learner and the prediction results are obtained respectively. Next, the prediction results of all base models are fed into the meta-learner and serve as meta-features. The meta-learner uses the results of the base learner to perform a new iteration calculation and give a final drilling efficiency prediction result. The framework of the stacking ensemble learning method is depicted in Fig. 2.

Table 1 Features that affect drilling efficiency

If the parameters are to be extended to other earth-rock excavation, some of the influencing factors can be reclassified or be adjusted as continuous variables as needed

As shown in Fig. 2, the training set of the original sample is={(x,y),=1, 2, …,,=1, 2, …,}, whereyrepresents the sample value of drilling efficiency corresponding to the feature vector (effect factors)x,is the number of features contained inx, andis the number of samples. We assume that there areheterogeneous base learners in the first layer, and the original dataset is divided equally intosubsets1,2, …,S. LetSbe the test set of the-fold in the process of-fold cross-validation, and the remaining set ofbe the training set. For the test setSof the-fold, the drilling efficiency prediction results of each base learnerare expressed as, and the corresponding sample set is denoted as, each of which containssamples,=/. Training and prediction are conducted successively. After all the base learners have completedcross-validations and predictions, a new data samplenewcontainingmeta-features will be formed:new={(,),=1, 2, …,,=1, 2, …,}. All the newly generated prediction results are taken as the input features of the meta-learner in the second layer. As can be observed from the above, in contrast to other ensemble learning strategies, the stacking strategy can fully use the prediction results of the first layer and original dataset for learning in the second layer to reduce the biases of the base learner layer and to improve the accuracy of the model prediction.

As mentioned above, the key to designing a framework for stacking ensemble learning is to enhance the diversity of the base models. In the first layer,base learners are generated using different algorithms. To obtain models with better generalization ability and accuracy under the premise of ensuring the diversity of ensemble members, an extensive experiment with different combinations of varying types and numbers of base learners, such as a gradient boosting decision tree (GBDT), XGBoost, BPNN, and SVR, were conducted. Similarly, diversified models, including ELM, SVR, DBN, and other algorithms, were constructed as meta-learners. The results demonstrate that the model achieved the best prediction performance when XGBoost, RF, and BPNN were used as the base learners, and SVR was used as the meta-learner. The base models are briefly introduced as follows.

4.2.1XGBoost

The core concept of XGBoost is the parallel of a massively boosted tree that combines several weak classifiers to develop a superior classifier with outstanding performance (Lv et al., 2020). Letfbe the model function of the decision tree at theth iteration. The complexity of each tree that splits the tree into a structure partand a leaf weight partis then expressed as:

whererepresents the total number of leaf nodes,is the weight coefficient used to control the leaf number,is the super parameter, andwrepresents the weight corresponding to theth leaf. To minimize the objective function, a method that adds the model function of the tree is adopted, which can consider the loss function of the lifting model of multiple trees:

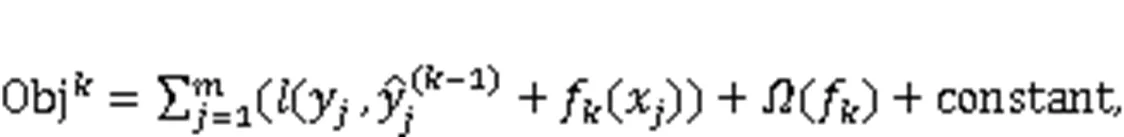
Fig. 2 Framework of the stacking ensemble learning method

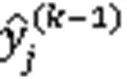
4.2.2RF

As a widely applied tool for classification and regression problems, RF integrates a variety of unrelated decision trees to mitigate the instability issue of each tree (Breiman, 2001). The main idea is to break down a complex decision into a sequence of simple decisions, thus providing a more explainable solution (Wang et al., 2007). The RF regression procedures are shown in Fig. S1 of the electronic supplementary materials (ESM).

4.2.3BPNN

BPNN is a kind of ANN which is widely applied in many practical forecasting problems (Wang et al., 2015; Mao et al., 2021). By constantly updating the connection weights between neurons and the neurons' weight thresholds, the error between the output value and the real value is propagated back to minimize the network error.is defined as the reverse error,wis the weight from the neurons of layerto the neurons of layer,ois the output of layer, and netis the weighted output of layer. The change inwis:

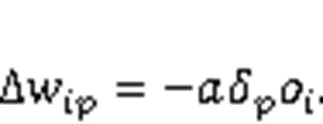
4.2.4SVR

SVR is an attractive tool for regression prediction that can fit in with a small set of input samples and overcome many problems such as dimension disaster and the local optimal solution (Kazemzadeh et al., 2020). For a given set of training samples={(x,y)|x∈R,y∈R,=1, 2, …}, the regression problem is simplified to find a function()such that the error between the predicted value and the expected valueis not greater than the given value. By introducing the insensitive loss function, SVR can be expressed as the following programming problem:

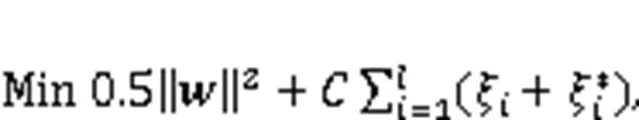
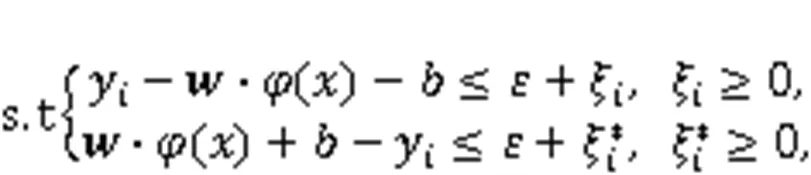
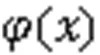
4.3 Parameter optimization based on ICSO

The performance of the base models in ensemble learning is susceptible to the changes of some important parameters. In the traditional XGBoost, RF, BPNN, and SVR, hyper-parameters are determined by expert's experience. However, in the process of drilling efficiency prediction, the sample data have the characteristics of complexity and multiformity. Selecting parameters based on experience usually fails to find the best parameter, often resulting in unreliable results. Random search and grid search have been used to optimize the model's parameters in previous studies. Nevertheless, the advantages of these methods will be limited when multi-parameter optimization problems are encountered, resulting in combinatorial explosion problems. The swarm intelligent algorithm performs better for this type of problem. Accordingly, to further strengthen the performance of the enhanced stacking-based model, we optimized the parameters of each base learner and meta-learner with ICSO.

The CSO is a new heuristic intelligent optimization algorithm proposed by Yang and Deb (2014), and exhibits good performance compared to other algorithms for optimization problems. Based on the simulation of cuckoo's nest-seeking behavior for laying eggs, the CSO combines Levy flight characteristics and the global optimization arithmetic of fruit fly (Meng et al., 2019; Li et al., 2021; Peng et al., 2021). The flight behavior of cuckoos looking for other nests has the characteristic of Levy flight in power-law steps. In Levy flight, a moving entity can occasionally take an unusually large step to change the behavior of a system. Its direction of motion is random, and the step size is distributed according to the power law. Various studies have shown that Levy flight performs well in solving optimization problems and searching optimization (Pavlyukevich, 2007). There are two types of search methods in CSO: global random search and local random search. In global random search, the cuckoo uses a Levy flight pattern to find a nest. The formula for updating the nest position with Levy flight is shown as:

X

t

+1

=

X

t

+

αL

(

s

,

λ

), (7)

whereis the step-size factor related to the scale of the problem.(,) denotes the Levy random walk path:

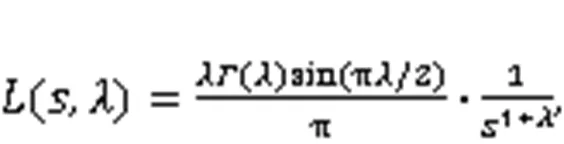
whereis the step length,>>0>0,0is a constant and normally taken as 0.01;is theLevy index, 1<<3, and usually=1.5;() is a function following the gamma distribution. Levy flight is divided into two steps: selection of random directions and generation of step length following the Levy distribution. The selection of random directions is uniformly distributed and the generation method of the step lengthis:

where～(0,2) and～(0, 1), both subject to a Gaussian distribution.2is calculated as:

The number of available host nests is fixed. When the host bird discovers, with a certain probability pa, that another cuckoo has laid an egg in its nest and a local random search is adopted to find another nest:

whereandare both random numbers subject to the uniform distribution; Heaviside(pa-) is the unit step function, andandare any other two nests.

However, in a basic CSO, the random step-sizeis a constant and is usually fixed as 1, resulting in a slower convergence rate. In this study, to improve the search speed and convergence rate,is set as a variable parameter that decreases as the iteration time increases, which means that more short-distance searches can be conducted when the population is close to the optimal solution. When initializing the parameters,maxandminare set. In the iteration process,is calculated as:

whereiter andmaxrepresent the current iteration times and the total number of iterations, respectively, and (min,max) is the range of the step-size parameter; the changes inare shown in Fig. S3 in ESM. Table S1 in ESM shows the pseudocode of the improved parameter optimization algorithm's development process for the prediction model.

4.4 Modeling of the ICSO-stacking ensemble learning

The modelling procedure for the proposed prediction method is illustrated in Fig. 3. Firstly, the pre-processed dataset including drilling efficiency and influencing factors is divided into five parts for the fivefold cross-validation, and the parameters of the ICSO are initialized. The second step is applied in the base learner layer of the model. The sample data are input into each base learner. Three base learners, ICSO-XGBoost, ICSO-RF, and ICSO-BPNN, are trained and tested, each providing an independent prediction result of drilling efficiency. The prediction results of the above base models are fed into the meta-learner layer and serve as meta-features. Finally, the newly generated prediction results are taken as the input to train and test the meta-learner ICSO-SVR in a new iteration of calculation that gives the final drilling efficiency prediction result.

Fig. 3 Flowchart of the proposed stacking prediction model

5 Case study

To verify the approach presented in this paper, data obtained from the quarry of a large rock-fill dam project under construction in southwest China were used as a proof of concept. Section 5.1 provides a brief description of the data collection for subsequent analysis. Section 5.2 describes the building of the stacking ensemble learning model, mainly including the selection of base learners and meta-learner. Then the parameter setting of each model is shown in Section 5.3. Finally, in Section 5.4, the prediction results and model performance are compared between the presented method and the currently popular model, demonstrating the superior performance and accuracy of the proposed stacking-based ensemble learning model.

5.1 Data collection

The engineering data came from two quarries of the high rock-fill dam project, whose excavation period was nearly seven years. Fig. 4 shows the drilling process applied to rock on site. It can be seen that the quarry is in the open air; therefore, unlike in underground engineering, the drilling process is affected by factors such as weather conditions. In the data collection process, different effecting factors are scattered across the drilling process and must be collected separately. Most of the data were recorded by supervisors on site, while the weather data were obtained from the on-site meteorological monitoring station. The weather conditions corresponding to each borehole were extracted from the database recorded by the meteorological monitoring station. We collected a total of 155 sets of drilling data. The data were normalized to a standard format for input to the model. Finally, a dataset with 155 rows and 12 columns was created.

5.2 Model building of stacking ensemble learning

5.2.1Setting of evaluation indicators

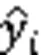
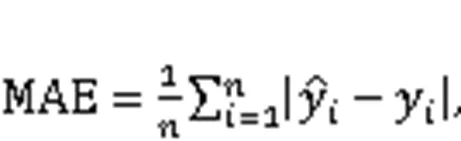
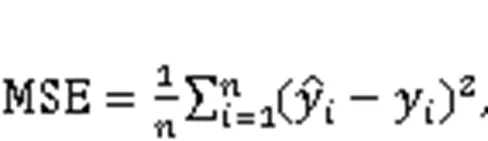
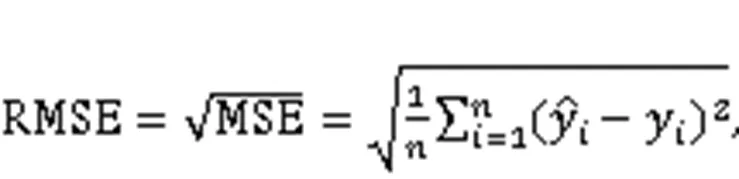
Fig. 4 Drilling operation in the quarry

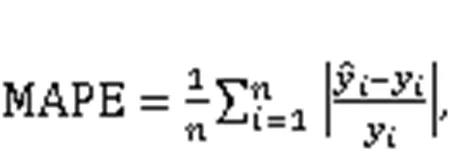
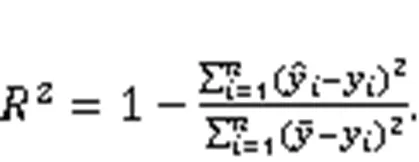
5.2.2Selection of the base learners

To select the base learners, we tested and compared the performance of several ML algorithms that at present perform well in the field of regression prediction in predicting the drilling efficiency, including network models, tree-based models, and regression models. The prediction performances of eight single ML models are shown in Fig. 5. The values of the evaluation indicators are listed in Table S2 in ESM. In addition, we calculated the mean, standard deviation, and coefficient of variation (CV) of indicators to measure their overall performance and the stability of different folds, as shown in Table S3 in ESM. The results indicate that XGBoost performs best overall and generates prediction results with the lowest errors of all the models, followed by RF and BPNN. For instance, in fold 1 of the dataset, the MAPE, MAE, MSE, RMSE, and2of deep belief network (DBN) are 0.853, 0.713, 0.840, 0.916, and -‍0.002, respectively, while XGBoost shows the most outstanding prediction performance, where MAPE, MAE, MSE, RMSE, and2are 0.140, 0.249, 0.186, 0.432, and 0.778, respectively. It can be found that these three base learners selected in this study have the best evaluation indicators compared with other models. Their standard deviation or CV are also within an acceptable range, with little fluctuation in five folds.

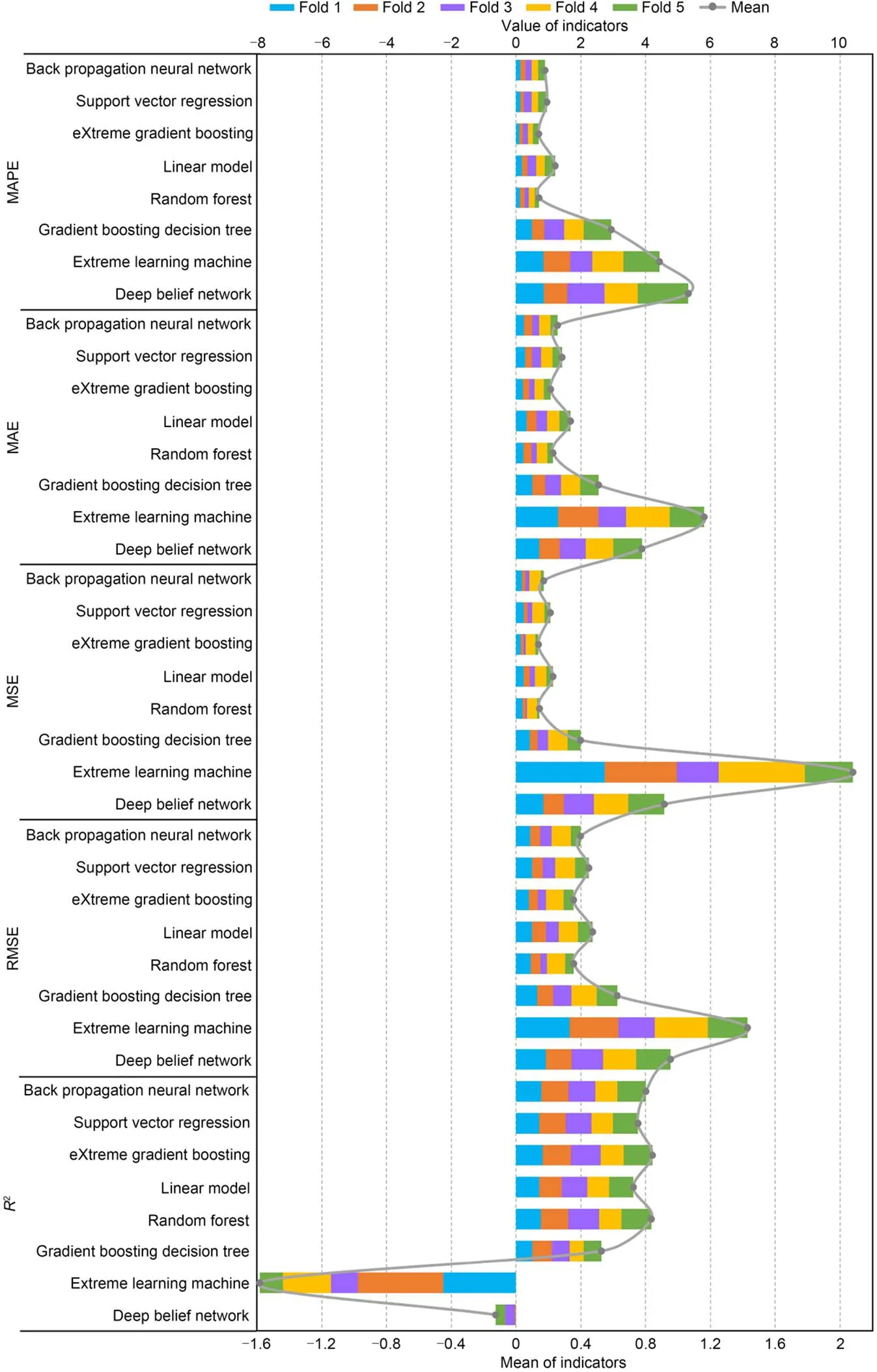
Fig. 5 Prediction performance of eight single ML models for base learner. References to color refer to the online version of this figure

In general, tree-based models outperform deep learning when small data volumes and many features are involved. Thus, RF and XGBoost exhibited excellent performance. Furthermore, BPNN also showed good performance and outperformed other models due to its excellent nonlinear fitting ability. In summary, XGBoost, RF, and BPNN are the top three ML models in prediction performance, and can provide accurate input for the meta-learner. Consequently, the three ML models were selected as the base learners of the stacking-based ensemble learning.

5.2.3Selection of the meta-learner

As with the base learner, several of popular ML (RF, GBDT, XGBoost, etc.) employed in current ensemble learning methods were compared to determine the best meta-learner. It was noted that ELM and DBN did not perform well in the base learner selection experiment, indicating that they are not suitable for drilling efficiency prediction. Thus, they were not considered for selection as meta-learner. The comparison results of the prediction performance of six meta-learners are presented in Fig. 6. The values of the corresponding evaluation indicators are listed in Table S4 in ESM. We also calculated the mean, standard deviation, and CV of the indicators in different meta-learner models to measure their overall performance and the stability of different folds, as shown in Table S5 in ESM. It can be observed that, although some indicators of the general linear model (LM) are slightly better than SVR in some fold, the indicators of SVR are the best in terms of mean and overall. The standard deviation or CV are also within an acceptable range, with little fluctuation in five folds. Therefore, on the whole, the prediction performance of SVR is absolutely better than that of the other five models.

To evaluate the prediction performance more comprehensively, we present the prediction results of six models in Fig. 7 and further calculate the Pearson correlation coefficient (PCC) between the actual samples and the predicted results. The computational formula of PCC is shown as follows and the result is presented in Fig. 7.

Fig. 6 Prediction performance of different single ML models as meta-learner. References to color refer to the online version of this figure

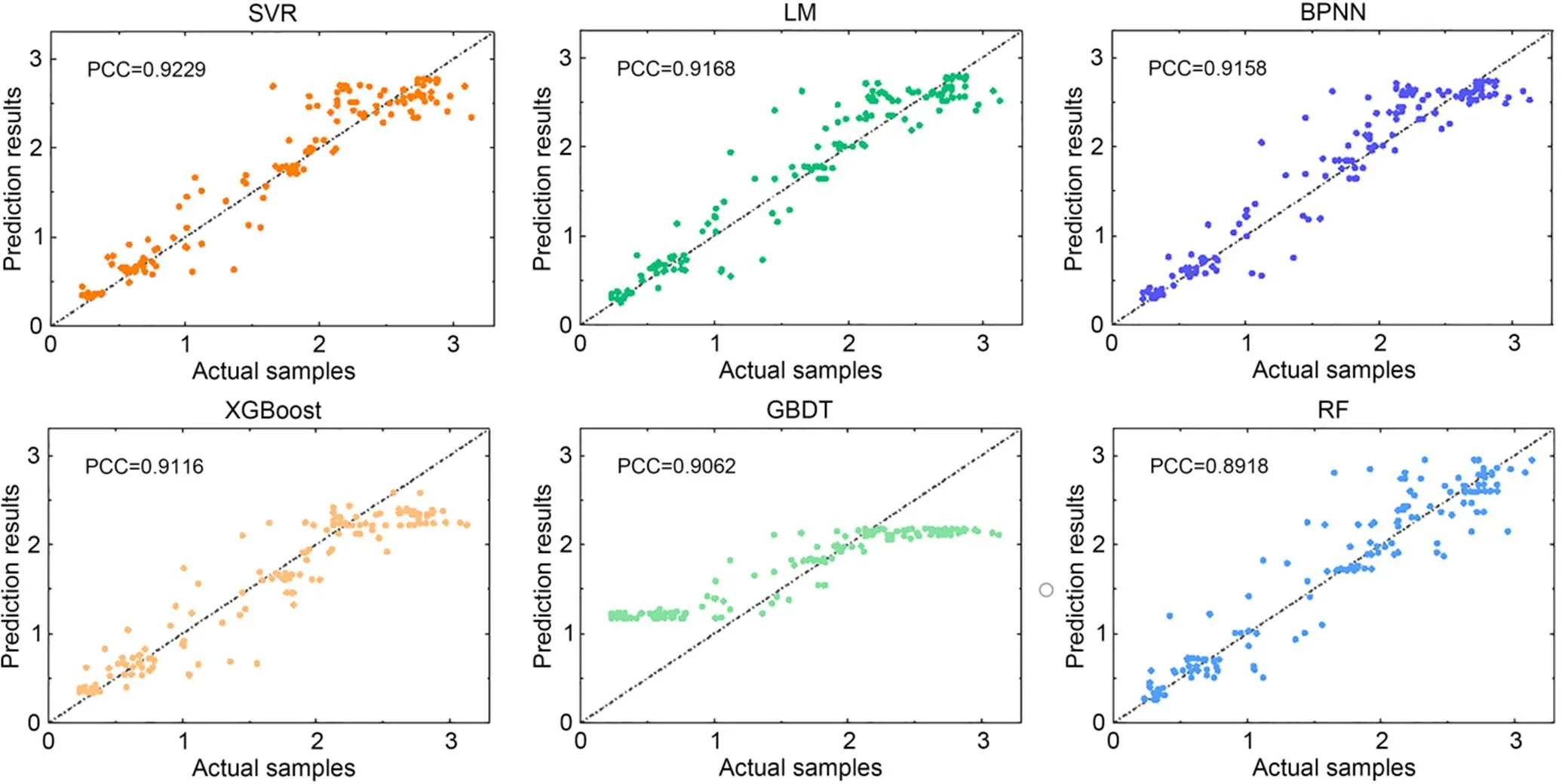
Fig. 7 Prediction results and PCC of the stacking model with different single ML models as meta-learner

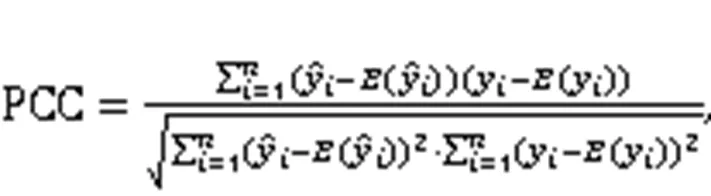
As shown in Fig. 7, the order of PCC between actual samples and prediction results is: SVR>LM>BPNN>XGBoost>GBDT>RF. The results further demonstrate the superiority of SVR over other ML models as the meta-learner for drilling efficiency prediction. From a theoretical point of view, this is because SVR is good for problems with a limited number of input samples and can overcome many problems such as dimension disaster and the local optimal solution. Thus SVR is selected as the meta-learner for the stacking-based ensemble learning.

5.2.4Performance evaluation

The prediction results of stacking-based ensemble learning using SVR as meta-learner and these three single models are shown in Fig. 8. It can be seen that the PCC of the ensemble learning is better than that of the three single models XGBoost, RF, and BPNN. From Figs. 5–8, it can be concluded that the stacking-based ensemble learning model can reduce the value of evaluation indicators and produce more accurate prediction results compared with the single ML models. In addition, the results also indicate that the ensemble learning model improved the performance of several heterogeneous ML models and that the effectiveness as well as the fitting ability of the ensemble model have been improved by introducing multiple single ML models. At this point, the ensemble learning model, including four base models RF, XGBoost, BPNN, and SVR, was built.

5.3 Parameter setting of each base model

ICSO was used for the stacking-based prediction model in this study to optimize the parameters. The computational experiments were conducted using a regular engineering workstation with an Intel i7-6700 CPU and GeForce GTX 970 under the Windows 10 operating system. The optimal parameters of each base learner were calculated based on ICSO. Then the final parameters of the ensemble learning model were adjusted accordingly, as shown in Table 2.

5.4 Prediction results and performance comparison

This study evaluated the effectiveness and showed the advantages of the proposed ensemble learning model over other ensemble learning models and single ML models for drilling efficiency prediction. Through a comparison in Section 5.2, it can be observed that the stacking ensemble learning composed of RF, XGBoost, and BPNN as the base learners and SVR as the meta-learner is the optimal model for drilling efficiency prediction. In this section, the prediction results of the proposed model are presented and the predictive performance on drilling efficiency is evaluated. The ICSO-stacking ensemble learning model was compared with XGBoost (the best performing single model in the aforementioned experiment), XGBoost optimized with ICSO, and the stacking model based on other intelligent optimization algorithms.

Fig. 8 Prediction results and PCC of the stacking-based ensemble learning and the three single models

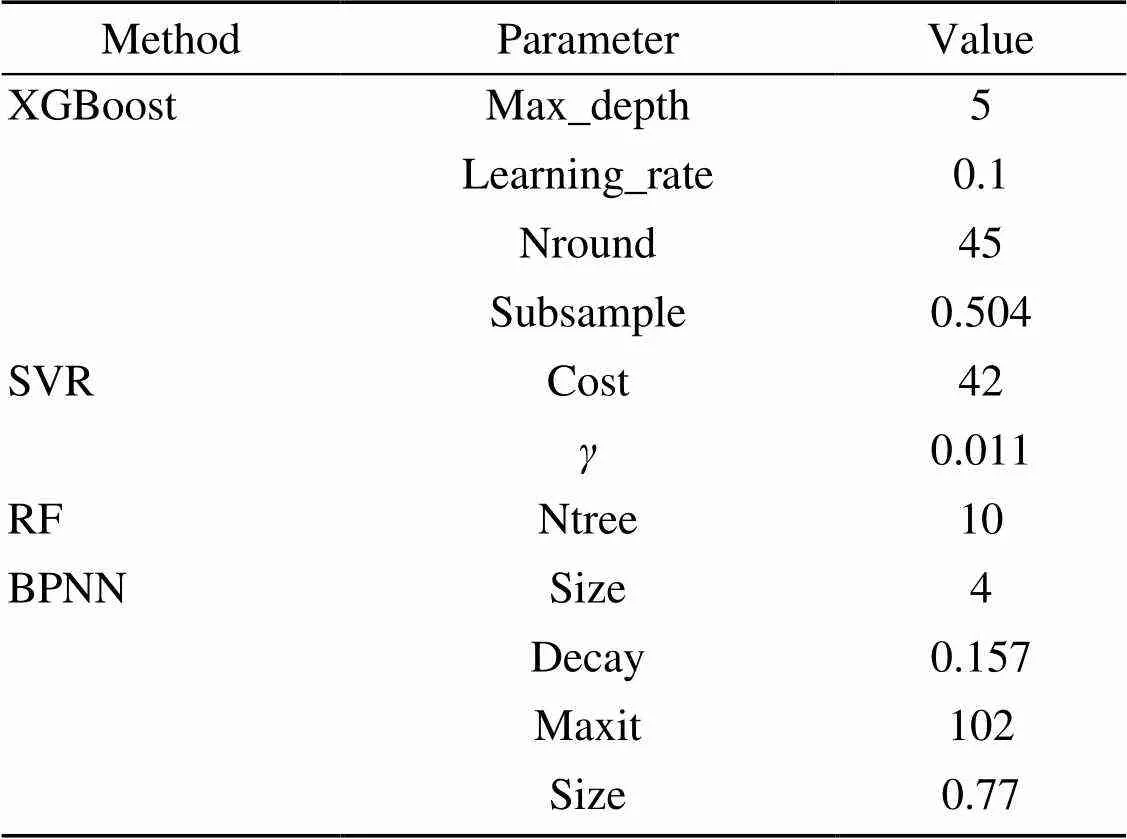
Table 2 Parameter setting of base learners and meta-learner after optimization

The prediction results of the proposed ICSO-stacking model and alternative prediction models are shown in Fig. 9. The PCC values between the prediction results and actual samples of ICSO-stacking, CSO-stacking, particle swarm optimization (PSO)‍-stacking, stacking, ICSO-XGBoost, and XGBoost are 0.9292, 0.9290, 0.9284, 0.9229, 0.9267, and 0.9163, respectively. We can see that the PCC of ICSO-stacking ensemble learning is the largest amongst all the models. It demonstrates that the prediction results of the proposed ICSO-stacking ensemble learning model are closer to actual samples than those of the alternative models.

To further validate the effectiveness of the proposed ensemble drilling efficiency prediction model, the comparison of evaluation indicators between ICSO-stacking and alternative prediction models was also carried out. The performance comparison in each fold is shown in Fig. 10 and the corresponding mean of evaluation indicators are presented in Table 3. As indicated in Table 3 and Figs. 9 and 10, we can draw the following conclusions:

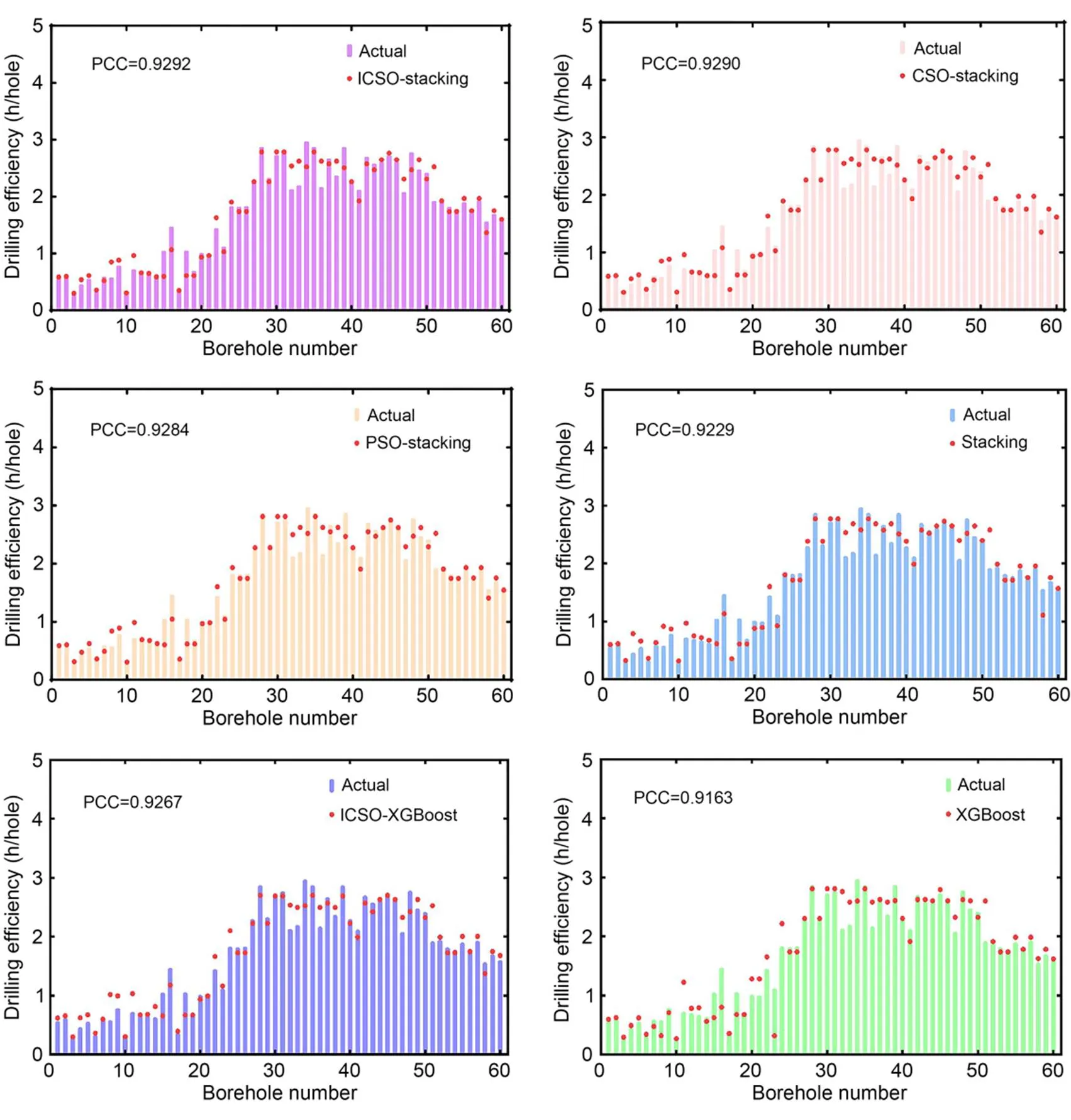
Fig. 9 Prediction results of the proposed model and alternative prediction models

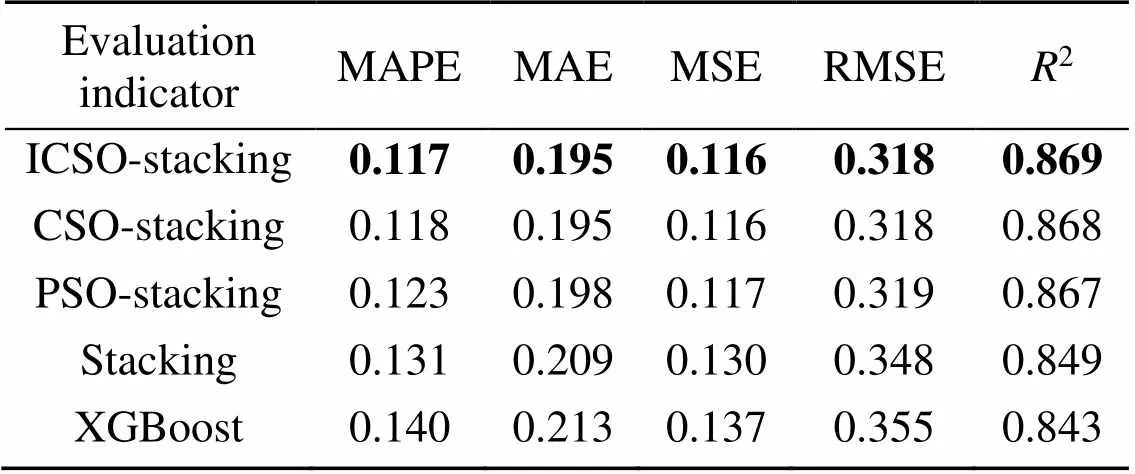
Table 3 Mean of evaluation indicators of different algorithms

The values in bold represent the best results of the evaluation indicators

Fig. 10 Performance comparison of proposed ensemble learning model and other algorithms

Firstly, the proposed ICSO-stacking drilling efficiency prediction method significantly outperforms the single ML models. The advantages of the proposed method are shown with comparisons. Taking the evaluation indicators of XGBoost as an example, the mean values of MAPE, MAE, MSE, RMSE, and2are 0.140, 0.213, 0.137, 0.355, and 0.843, respectively. The same evaluation indicators of the proposed ICSO-stacking method are 0.117, 0.195, 0.116, 0.318, and 0.869, which are 16.43%, 8.45%, 15.33%, 10.42% lower and 3.08% higher than XGBoost. The results demonstrate that the predictive performance and fitting ability of the model all greatly exceed that of XGBoost and other single ML algorithms.

Secondly, the ICSO-stacking proposed ensemble model has better prediction accuracy than general ensemble learning models. In other words, using intelligence optimization algorithms to optimize parameters can improve the performance of the stacking-based model. The mean values of MAPE, MAE, MSE, RMSE, and2of the general ensemble learning built in this study are 0.131, 0.209, 0.130, 0.348, and 0.849, respectively. In contrast, the same evaluation indicators of the proposed ICSO-stacking method are reduced by 10.69%, 6.70%, 10.77%, 8.62% and improved by 2.36%, respectively. Therefore, for multi-parameter optimization, the swarm intelligent algorithm performed more efficiently than other existing parameter adjustment methods.

Thirdly, ICSO incorporating the dynamically updating step-size parameter was used to optimize the parameters of the base learners and meta-learner, further enhancing the predictive power of the model. To prove the superiority of ICSO, the standard CSO and PSO were used for comparison. Four Benchmark functions were used to test the performance, the results are shown in Section S1 of ESM. The convergence process of the three intelligent algorithms for this study is illustrated in Fig. 11. It can be concluded that ICSO could find the optimal solution earlier with a better convergence speed as well as displaying more effective performance and smaller prediction error compared with the standard CSO and PSO.

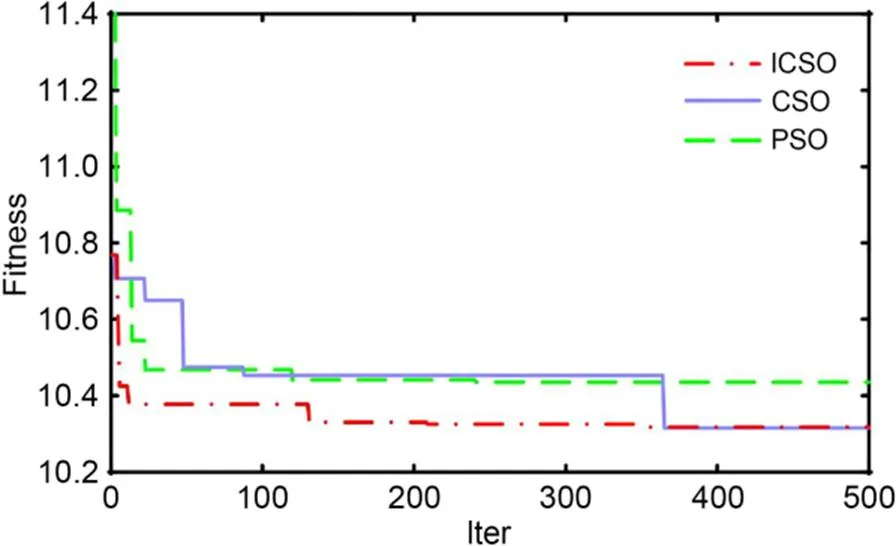
Fig. 11 Convergence process of fitness index for different intelligent algorithms

6 Conclusions

A novel drilling efficiency prediction method was proposed in this study, combining the advantages of the swarm intelligent algorithm and stacking-based ensemble learning.

This study has made some contributions. Firstly, through experimental comparison, four different models, XGBoost, RF, BPNN, and SVR, were selected to generate an ensemble learning model for predicting drilling efficiency. Secondly, the comprehensive effects of various factors including environment and operation are considered quantitatively. Thirdly, the ICSO with an adaptive step-size strategy was proposed to optimize the hyper-parameter of the model. Finally, we verified the effectiveness of the proposed model for drilling efficiency prediction through five-fold cross-validation experiments. A major advantage of the proposed ensemble method is that multiple single ML methods are combined, which enhances the fitting ability of the individual models and handles regression prediction with limited data more accurately. Compared with the XGBoost and PSO-stacking methods, our ICSO-stacking ensemble method reduced the MAPE by 16.43% and 4.88%, respectively, proving that the proposed method could provide more reliable decision support for drilling procedures and excavation scheduling.

Future work can be conducted exploring the following: firstly, more features of the prediction model can be collected to further improve prediction accuracy; secondly, the selection of the optimal combination of base models is not very efficient and thus a more automated and intelligent selection system needs to be developed for combining the base models automatically.

Acknowledgments

This work is supported by the Yalong River Joint Funds of the National Natural Science Foundation of China (No. U1965207) and the National Natural Science Foundation of China (Nos. 51839007, 51779169, and 52009090).

Author contributions

Jia YU designed the research. Fei LV processed the corresponding data. Fei LV and Jun ZHANG wrote the first draft of the manuscript. Peng YU and Da-wei TONG helped to organize the manuscript. Jia YU and Bin-ping WU revised and edited the final version.

Conflict of interest

Fei LV, Jia YU, Jun ZHANG, Peng YU, Da-wei TONG, and Bin-ping WU declare that they have no conflict of interest.

Electronic supplementary materials

Figs. S1–S4, Tables S1–S6, and Section S1

Abbas AK, Rushdi S, Alsaba M, et al., 2019. Drilling rate of penetration prediction of high-angled wells using artificial neural networks. Journal of Energy Resources Technology, 141(11):112904. https://doi.org/10.1115/1.4043699

Abbaspour H, Drebenstedt C, Badroddin M, et al., 2018. Optimized design of drilling and blasting operations in open pit mines under technical and economic uncertainties by system dynamic modelling. International Journal of Mining Science and Technology, 28(6):839-848. https://doi.org/10.1016/j.ijmst.2018.06.009

Abu Bakar MZ, Butt IA, Majeed Y, 2018. Penetration rate and specific energy prediction of rotary-percussive drills using drill cuttings and engineering properties of selected rock units. Journal of Mining Science, 54(2):270-284. https://doi.org/10.1134/S106273911802363X

Akün ME, Karpuz C, 2005. Drillability studies of surface-set diamond drilling in Zonguldak region sandstones from Turkey. International Journal of Rock Mechanics and Mining Sciences, 42(3):473-479. https://doi.org/10.1016/j.ijrmms.2004.11.009

Breiman L, 2001. Random forests. Machine Learning, 45(1):5-32. https://doi.org/10.1023/A:1010933404324

Bui DT, Nhu VH, Hoang ND, 2018. Prediction of soil compression coefficient for urban housing project using novel integration machine learning approach of swarm intelligence and multi-layer perceptron neural network. Advanced Engineering Informatics, 38:593-604. https://doi.org/10.1016/j.aei.2018.09.005

Cankurt S, Subasi A, 2022. Tourism demand forecasting using stacking ensemble model with adaptive fuzzy combiner. Soft Computing, 26(7):3455-3467. https://doi.org/10.1007/s00500-021-06695-0

Chen KL, Jiang JC, Zheng FD, et al., 2018. A novel data-driven approach for residential electricity consumption prediction based on ensemble learning. Energy, 150:49-60. https://doi.org/10.1016/j.energy.2018.02.028

Chen WL, Wang XL, Cai ZJ, et al., 2021. DP-GMM clustering-based ensemble learning prediction methodology for dam deformation considering spatiotemporal differentiation. Knowledge-Based Systems, 222:106964. https://doi.org/10.1016/j.knosys.2021.106964

Cui SZ, Yin YQ, Wang DJ, et al., 2021. A stacking-based ensemble learning method for earthquake casualty prediction. Applied Soft Computing, 101:107038. https://doi.org/10.1016/j.asoc.2020.107038

Darbor M, Faramarzi L, Sharifzadeh M, 2019. Performance assessment of rotary drilling using non-linear multiple regression analysis and multilayer perceptron neural network. Bulletin of Engineering Geology and the Environment, 78(3):1501-1513. https://doi.org/10.1007/s10064-017-1192-3

Elkatatny S, 2018. Application of artificial intelligence techniques to estimate the static Poisson’s ratio based on wireline log data. Journal of Energy Resources Technology, 140(7):072905. https://doi.org/10.1115/1.4039613

Galar M, Fernandez A, Barrenechea E, et al., 2012. A review on ensembles for the class imbalance problem: bagging-, boosting-, and hybrid-based approaches. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 42(4):463-484. https://doi.org/10.1109/TSMCC.2011.2161285

Gan C, Cao WH, Wu M, et al., 2019. Prediction of drilling rate of penetration (ROP) using hybrid support vector regression: a case study on the Shennongjia area, central China. Journal of Petroleum Science and Engineering, 181:106200. https://doi.org/10.1016/j.petrol.2019.106200

Guo YY, Wang X, Xiao PC, et al., 2020. An ensemble learning framework for convolutional neural network based on multiple classifiers. Soft Computing, 24(5):3727-3735. https://doi.org/10.1007/s00500-019-04141-w

Haghighi F, Omranpour H, 2021. Stacking ensemble model of deep learning and its application to Persian/Arabic handwritten digits recognition. Knowledge-Based Systems, 220:106940. https://doi.org/10.1016/j.knosys.2021.106940

Hustrulid WA, Kuchta M, Martin R, 2013. Open Pit Mine Planning and Design, 3rd Edition. Taylor & Francis, Boca Raton, Florida, USA.

Kahraman S, 2002. Correlation of TBM and drilling machine performances with rock brittleness. Engineering Geology, 65(4):269-283. https://doi.org/10.1016/s0013-7952(01)00137-5

Kahraman S, Bilgin N, Feridunoglu C, 2003. Dominant rock properties affecting the penetration rate of percussive drills. International Journal of Rock Mechanics and Mining Sciences, 40(5):711-723. https://doi.org/10.1016/s1365-1609(03)00063-7

Kaushik A, Kaur P, Choudhary N, et al., 2022. Stacking regularization in analogy-based software effort estimation. Soft Computing, 26(3):1197-1216. https://doi.org/10.1007/s00500-021-06564-w

Kazemzadeh MR, Amjadian A, Amraee T, 2020. A hybrid data mining driven algorithm for long term electric peak load and energy demand forecasting. Energy, 204:117948. https://doi.org/10.1016/j.energy.2020.117948

Koopialipoor M, Tootoonchi H, Armaghani DJ, et al., 2019. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bulletin of Engineering Geology and the Environment, 78(8):‍6347-6360. https://doi.org/10.1007/s10064-019-01538-7

Li H, Wang XS, Ding SF, 2018. Research and development of neural network ensembles: a survey. Artificial Intelligence Review, 49(4):455-479. https://doi.org/10.1007/s10462-016-9535-1

Li LL, Cen ZY, Tseng ML, et al., 2021. Improving short-term wind power prediction using hybrid improved cuckoo search arithmetic-support vector regression machine. Journal of Cleaner Production, 279:123739. https://doi.org/10.1016/j.jclepro.2020.123739

Li SP, 2018. Research on Excavation Simulation of a Pumped Storage Power Station Based on Excavation and Filling Balance. MS Thesis, Tianjin University, Tianjin, China(in Chinese).

Li ZX, Wu DZ, Hu C, et al., 2019. An ensemble learning-based prognostic approach with degradation-dependent weights for remaining useful life prediction. Reliability Engineering & System Safety, 184:110-122. https://doi.org/10.1016/j.ress.2017.12.016

Lv F, Wang JJ, Cui B, et al., 2020. An improved extreme gradient boosting approach to vehicle speed prediction for construction simulation of earthwork. Automation in Construction, 119:103351. https://doi.org/10.1016/j.autcon.2020.103351

Mao CY, Lin RR, Towey D, et al., 2021. Trustworthiness prediction of cloud services based on selective neural network ensemble learning. Expert Systems with Applications, 168:114390. https://doi.org/10.1016/j.eswa.2020.114390

Mendes-Moreira J, Soares C, Jorge AM, et al., 2012. Ensemble approaches for regression: a survey. ACM Computing Surveys, 45(1):10. https://doi.org/10.1145/2379776.2379786

Meng XJ, Chang JX, Wang XB, et al., 2019. Multi-objective hydropower station operation using an improved cuckoo search algorithm. Energy, 168:425-439. https://doi.org/10.1016/j.energy.2018.11.096

Mustafa AB, Abbas AK, Alsaba M, et al., 2021. Improving drilling performance through optimizing controllable drilling parameters. Journal of Petroleum Exploration and Production, 11(3):1223-1232. https://doi.org/10.1007/s13202-021-01116-2

Paul A, Bhowmik S, Panua R, et al., 2018. Artificial neural network-based prediction of performances-exhaust emissions of diesohol piloted dual fuel diesel engine under varying compressed natural gas flowrates. Journal of Energy Resources Technology, 140(11):112201. https://doi.org/10.1115/1.4040380

Pavlyukevich I, 2007. Lévy flights, non-local search and simulated annealing. Journal of Computational Physics, 226(2):1830-1844. https://doi.org/10.1016/j.jcp.2007.06.008

Peng H, Zeng ZG, Deng CS, et al., 2021. Multi-strategy serial cuckoo search algorithm for global optimization. Knowledge-Based Systems, 214:106729. https://doi.org/10.1016/j.knosys.2020.106729

Pernía-Espinoza A, Fernandez-Ceniceros J, Antonanzas J, et al., 2018. Stacking ensemble with parsimonious base models to improve generalization capability in the characterization of steel bolted components. Applied Soft Computing, 70:737-750. https://doi.org/10.1016/j.asoc.2018.06.005

Qi CC, Fourie A, Chen QS, 2018. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Construction and Building Materials, 159:473-478. https://doi.org/10.1016/j.conbuildmat.2017.11.006

Ren QB, Li MC, Song LG, et al., 2020. An optimized combination prediction model for concrete dam deformation considering quantitative evaluation and hysteresis correction. Advanced Engineering Informatics, 46:101154. https://doi.org/10.1016/j.aei.2020.101154

Saeidi O, Torabi SR, Ataei M, et al., 2014. A stochastic penetration rate model for rotary drilling in surface mines. International Journal of Rock Mechanics and Mining Sciences, 68:55-65. https://doi.org/10.1016/j.ijrmms.2014.02.007

Salimi A, Rostami J, Moormann C, et al., 2016. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunnelling and Underground Space Technology, 58:236-246. https://doi.org/10.1016/j.tust.2016.05.009

Shi X, Liu G, Gong XL, et al., 2016. An efficient approach for real-time prediction of rate of penetration in offshore drilling. Mathematical Problems in Engineering, 2016:3575380. https://doi.org/10.1155/2016/3575380

Wang H, Zhang YM, Mao JX, et al., 2020. A probabilistic approach for short-term prediction of wind gust speed using ensemble learning. Journal of Wind Engineering and Industrial Aerodynamics, 202:104198. https://doi.org/10.1016/j.jweia.2020.104198

Wang L, Zeng Y, Chen T, 2015. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Systems with Applications, 42(2):855-863. https://doi.org/10.1016/j.eswa.2014.08.018

Wang N, Zhao SY, Cui SZ, et al., 2021. A hybrid ensemble learning method for the identification of gang-related arson cases. Knowledge-Based Systems, 218:106875. https://doi.org/10.1016/j.knosys.2021.106875

Wang RC, Wu S, 2019. Neural network model based prediction of fragmentation of blasting using the Levenberg-Marquardt algorithm. Journal of Hydroelectric Engineering, 38(7):100-109 (in Chinese). https://doi.org/10.11660/slfdxb.20190710

Wang T, Li ZJ, Yan YJ, et al., 2007. A survey of fuzzy decision tree classifier methodology. Proceedings of the Second International Conference of Fuzzy Information and Engineering, p.959-968. https://doi.org/10.1007/978-3-540-71441-5_104

Yan T, Shen SL, Zhou AN, et al., 2022. Prediction of geological characteristics from shield operational parameters by integrating grid search and K-fold cross validation into stacking classification algorithm. Journal of Rock Mechanics and Geotechnical Engineering, 14(4):1292-1303. https://doi.org/10.1016/j.jrmge.2022.03.002

Yang XS, Deb S, 2014. Cuckoo search: recent advances and applications. Neural Computing and Applications, 24(1):169-174. https://doi.org/10.1007/s00521-013-1367-1

Zhang XH, Zhu QX, He YL, et al., 2018. A novel robust ensemble model integrated extreme learning machine with multi-activation functions for energy modeling and analysis: application to petrochemical industry. Energy, 162:593-602. https://doi.org/10.1016/j.energy.2018.08.069

https://doi.org/10.1631/jzus.A2200297

Jia YU, https://orcid.org/0000-0003-1775-1006

June 4, 2022; Revision accepted Aug. 31, 2022;

Crosschecked Sept. 28, 2022

© Zhejiang University Press 2022