饲料成本“保险+期货”模式稳定猪肉市场价格波动的效果研究*——基于非对称价格波动传导机制视角

潘方卉，王 宁，朱枨梓

（东北农业大学经济管理学院，黑龙江哈尔滨 150030）

0 引言

中国是猪肉消费和生产大国，猪肉是中国居民消费的主要肉类产品，2018年城镇和农村居民肉类消费量中猪肉占比分别稳定在72%和84%左右[1]，因此保障猪肉供应是关乎民生的重要问题，也是中央政府一直致力实现的政策目标①2017—2021年连续5年的“中央一号文件”提到生猪稳定保供是中国政府重要的政策目标。自1985年猪肉市场化改革以来，猪肉价格波动频繁且剧烈，形成了著名的“猪周期”问题。当猪肉价格上涨时，消费者（尤其是贫困人口）的生活成本将大幅提升，不利于广大居民的营养膳食；当猪肉价格下跌时，养殖户收入降低，从而改变投资策略，减少生猪存栏量，导致猪肉供给量下降，不利于生猪产业的持续健康发展。众多研究表明农产品价格过度波动比农产品价格过高更加危险[2]，因此缓解猪肉市场价格波动一直是亟待解决的社会焦点问题。

为了解决“猪周期”问题，政府推出饲料成本“保险+期货”模式，由于饲料成本占养殖成本的比重最高，约占50%～70%[3]。因此，稳定饲料成本有助于稳定生猪供给，进而实现稳定猪肉市场价格的政策目标，这是饲料成本“保险+期货”模式稳定猪肉市场价格波动的基本原理。由于玉米占饲料成本的比重可达60%[1]，因此文章将重点考察玉米价格“保险+期货”模式能否起到稳定猪肉市场价格的作用？作用效果如何？作用效果会受到哪些因素的影响？这些问题是该文研究的重点，而价格波动传导机制为解决上述问题提供了理论依据和方法支撑。

价格波动传导机制，也称为价格波动溢出效应，是指一个市场价格波动对另一个市场价格波动的影响程度和过程[3]。Apergis and Rezitis[4]提出如果产业链上各环节之间存在着价格波动传导机制，那么某一个环节上制定的价格调控政策，就可以起到稳定其他环节价格波动的作用；相反，如果产业链上各环节之间不存在着价格波动传导机制，那么产业链上某个环节的价格稳定政策就无法起到稳定其他环节价格波动的作用，此时政策制定者应该针对不同环节制定不同的价格稳定策略[5]。据此可知，如果玉米、生猪和猪肉市场之间存在价格波动传导机制，那么饲料成本“保险+期货”模式就可以通过稳定玉米价格来实现降低猪肉市场价格波动的政策目标。如果玉米、生猪和猪肉市场之间价格波动的关联程度越高，那么饲料成本“保险+期货”模式的作用效果就越显著。总之，饲料成本“保险+期货”模式稳定猪肉价格的作用效果依赖于玉米、生猪和猪肉市场之间的价格波动溢出效应和关联程度。有鉴于此，文章应用非对称BEKK-MGARCH模型检验生猪产业链上各环节（上游玉米、中游生猪和下游猪肉）之间的非对称价格波动传导机制，基于DCC-MGARCH模型，分析玉米、生猪和猪肉市场之间的动态相关程度，借以评价饲料成本“保险+期货”模式稳定猪肉市场价格波动的效果。

该文的边际贡献主要有3点：首先，从研究视角来看，以往文献大多研究农产品价格传导机制，很少研究农产品价格波动传导机制[6]，对农产品非对称价格波动传导机制的研究就更为少见[7]，然而鲜有研究表明农产品价格增加和减少会产生同样的价格传导波动溢出效应[8]，因此该文将基于非对称价格波动传导视角展开研究。其次，从研究对象来看，以往研究大多基于粮食和蔬菜等种植业，较少涉及养殖业，鉴于猪肉在中国居民饮食中的重要地位以及“猪周期”问题带来的较大社会负面效应，该文将以生猪产业作为研究对象。最后，从研究内容来看，还未有学者基于产业链上价格波动传导机制视角，研究饲料成本“保险+期货”模式稳定猪肉价格波动的效果，该文研究表明玉米、生猪和猪肉市场之间的价格波动传导机制和关联程度会影响饲料成本“保险+期货”模式的实施效果。该文剩余部分的结构安排如下：第一部分为文献综述，第二部分为研究方法，第三部分是数据说明与模型形式选择，第四部分是结果与分析，第五部分是主要结论和政策启示。

1 文献综述

自2007—2009年全球食品价格危机以来，农产品价格波动已经成为社会各界关注的焦点，越来越多的学者开始研究农产品产业链上价格波动传导机制。Assefa等[6]回顾和总结了农产品产业链上价格波动传导机制的相关研究文献。

在价格波动传导机制研究中，最早应用的是单变量广义自回归条件异方差（GARCH）模型。Natcher和Weaver[9]应用GARCH模型研究美国牛肉产业链中各个环节之间的价格波动溢出效应。Buguk等[10]建立EGARCH模型分析美国鲶鱼批发供应链中饲料、养殖和批发价格之间的波动溢出效应。同样，Uchezuba等[11]应用EGARCH模型研究南非鸡肉从农场到零售环节的价格波动溢出效应。由于单变量GARCH族模型仅能揭示农产品产业链上不同环节之间的单向价格波动溢出效应，因此，能够反映多向价格波动溢出效应的多变量广义自回归条件异方差（MGARCH）模型被提出，并得到了广泛的应用。Apergis和Rezitis[3]使用MGARCH模型检验希腊农业投入、生产以及零售环节之间的价格波动溢出效应。Rezitis和Stavropoulos[12]分别使用DVEC-MGARCH（1,1）和BEKK-MGARCH（1,1）检验希腊肉鸡行业中消费者和生产者之间的价格波动传导机制。Sidhoum和Serra[13]应用MGARCH模型评估西班牙番茄产业链上的价格波动溢出效应。Hassouneh等[14]应用MGARCH模型研究斯洛文尼亚小麦市场上价格波动溢出效应。

对于中国学者来说，农产品价格波动传导机制的研究主要集中于三个方面：一是国内外农产品市场之间的价格波动传导机制研究。例如：肖小勇等[15]应用BEKK-MGARCH研究了国内外粮价的波动传导机制。李光泗等[16]应用BEKK-MGARCH方法，分别基于粮食市场开放与进口快速增长的背景，研究国内外粮价波动溢出效应。高群、柯杨敏[18]从能源化视角探讨国内外食糖市场之间的价格波动溢出效应。严哲人等[19]运用滚动协整分析法和BEKK-GARCH模型，分析国内外原料奶市场之间的价格波动溢出效应。徐媛媛等[20]研究国际、国内玉米市场与国际原油市场之间的价格波动溢出效应。二是国内不同农产品市场之间的价格波动传导机制研究。吴海霞、王静[21]和韩啸[22]研究了小麦、玉米以及大豆市场之间的价格波动溢出效应；李辛一等[23]应用BEEK-GARCH等模型研究玉米期货与现货市场之间的价格波动溢出效应；丁存振和郑燕[24]通过构建VAR-BEKK-MVGARCH-DUMMY-T模型，从市场间溢出效应和动态关联两个方面研究了价格支持政策对棉花期现货市场关联的影响。三是农产品产业链上各环节之间价格波动传导机制研究。李秋萍[25]以及高群、宋长明[26]分别对生猪和肉鸡产业链上各环节之间的价格波动溢出效应进行研究；郑燕等[27]运用BEKK-MGARCH模型研究鸡蛋产业链上价格波动溢出效应。白宇航、张立中[28]运用BEKKMGARCH模型研究乳制品产业链上价格波动溢出效应。

上述国内外学者的研究均没有关注农产品市场价格波动传导的非对称性特征，但是有些学者关注于粮食和能源市场之间的非对称价格波动传导机制[29,30][7]，以及能源与金融市场之间的非对称价格波动传导机制[31-33]，这些能源、金融以及农产品市场间的非对称价格波动传导机制研究为该文提供了重要参考与借鉴。由此可见，农产品价格波动传导机制研究得到了国内外学者的广泛关注，研究方法主要集中于BEKK-MGARCH和DCC-MGARCH模型。然而，农产品产业链上非对称价格波动传导机制的研究较为鲜见，而生猪产业链上的非对称价格波动传导则更是缺乏。有鉴于此，该文将基于非对称价格波动传导视角，以生猪产业链为例，对饲料成本“保险+期货”模式稳定猪肉价格波动的效果进行评价，以期从研究视角、对象和内容三个方面对以往研究文献进行完善和补充。

2 研究方法

2.1 非对称BEKK-MGARCH模型

为了观测到不同市场之间的价格波动溢出效应，Engle和Kroner[34]提出了BEEK-MGARCH模型，但是该模型无法捕捉市场之间的非对称价格波动传导效应。因此，选取Kroner和Ng[35]提出的非对称BEEKMGARCH模型，该模型可以检验一个市场价格的增加与降低对其他市场价格是否有着同样的影响。

非对称BEKK-MGARCH模型主要包括两个方程：条件均值方程和条件方差方程。选择包括3个价格变量的向量自回归模型（Vector Autoregression，VAR）作为条件均值方程，具体形式为：

条件方差方程可表示为：

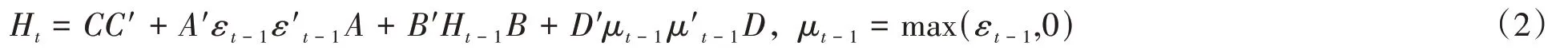
2.2 DCC-MGARCH模型

计算不同市场之间条件相关系数的模型主要有CCC-MGARCH和DCC-MGARCH两种，CCCMGRACH模型可以得到市场之间的静态条件相关系数，而DCC-MGRACH模型可以得出动态条件相关系数，能够有效地描述不同市场之间的动态关联程度。因此，采用Engle[36]提出的DCC-MGARCH模型来探究玉米、生猪和猪肉市场价格之间的动态关联程度。

在模型设定过程中，首先假设VAR模型的残差项服从正态分布过程N(0,Ht)，方差协方差矩阵Ht=DtRtDt，其中，Rt是动态相关系数矩阵，Dt中对角线上的元素为玉米、生猪和猪肉价格增长率序列的时变条件标准差矩阵，diag代表对角矩阵。

DCC-MGRACH模型的具体形式为：

为了确保R是正定矩阵且其所有的参数都≤1，Rt矩阵可以被描述成为：Q是标准化残差项的无条件方差矩阵，当Qt为正定或半正定时，Q*t保证相关系数矩阵Rt对角元素为1，且非对角元素的绝对值小于1。参数α和β是非负的，分别为前期标准化残差平方与前期条件方差的系数，且α+β≤1。

3 数据说明与模型形式选择

3.1 数据说明与处理

该文选择生猪产业链上的上游玉米价格、中游生猪价格和下游猪肉价格（单位：元/kg）作为研究对象，样本区间为2000年1月至2020年9月，数据来源于《布瑞克农业数据库》。具体数据处理过程如下：首先以2000年1月CPI作为基期，剔除玉米（pc）、生猪（ph）和猪肉（pp）价格序列中的通货膨胀因素，得到实际玉米、生猪和猪肉价格数据。然后，运用X13方法对实际价格序列进行季节调整，剔除季节因素的影响。再次，为了降低数据的异方差性，对时间序列进行取对数处理，得到取对数后的玉米价格（lpc）、生猪价格（lph）和猪肉价格（lpp）。最后，再进行一阶差分处理，得到玉米价格增长率（dlph）、生猪价格增长率（dlph）和猪肉价格增长率序列（dlpp）。图1和图2分别给出玉米、生猪和猪肉价格及其增长率序列的动态走势图。

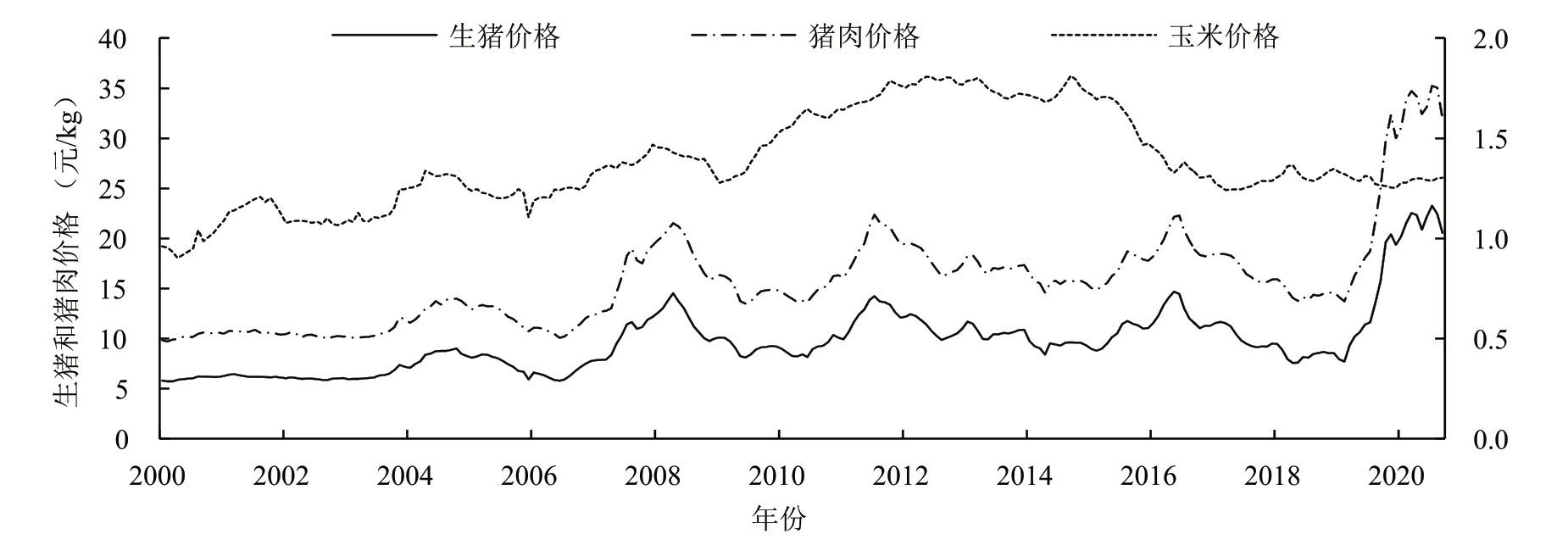
图1 2000—2019年玉米、生猪和猪肉价格动态走势

在图1中，左侧坐标轴表示生猪和猪肉价格，右侧坐标轴表示玉米价格。从图1中可以清晰地看到生猪和猪肉价格走势基本一致，均呈现出5次周期性波动。值得注意的是，2018年8月非洲猪瘟的爆发导致生猪和猪肉价格在2019年初开始大幅度上涨，快速上升到了历史最高点。对于玉米价格来说，在2008年之前，玉米与生猪（猪肉）价格呈现出相似的周期波动和长期走势。然而，在2008年之后，玉米临时收储政策的实施导致玉米价格不断提升。直到2015年，中国首次下调玉米的临时储备收购价格，随后2016年取消玉米临时储备政策，转为“市场化收购”加“补贴”的新机制，玉米价格的市场化改革使得玉米价格在2015—2016年显著下降。为此，国家开始实施推动乙醇工业发展等一系列调整政策，增加玉米需求，随后玉米价格才逐步趋于稳定。由此可见，玉米临时储备政策的实施使得玉米价格与生猪（猪肉）价格走势出现偏离。

图2给出了玉米、生猪和猪肉价格增长率序列（dlpc、dlph、dlpp）的动态走势图。从图2中可以看出玉米、生猪和猪肉价格增长率序列均表现出一定的波动性聚集现象，即小幅波动后往往跟着小幅度的波动，大幅度波动后往往跟着大幅度的波动。

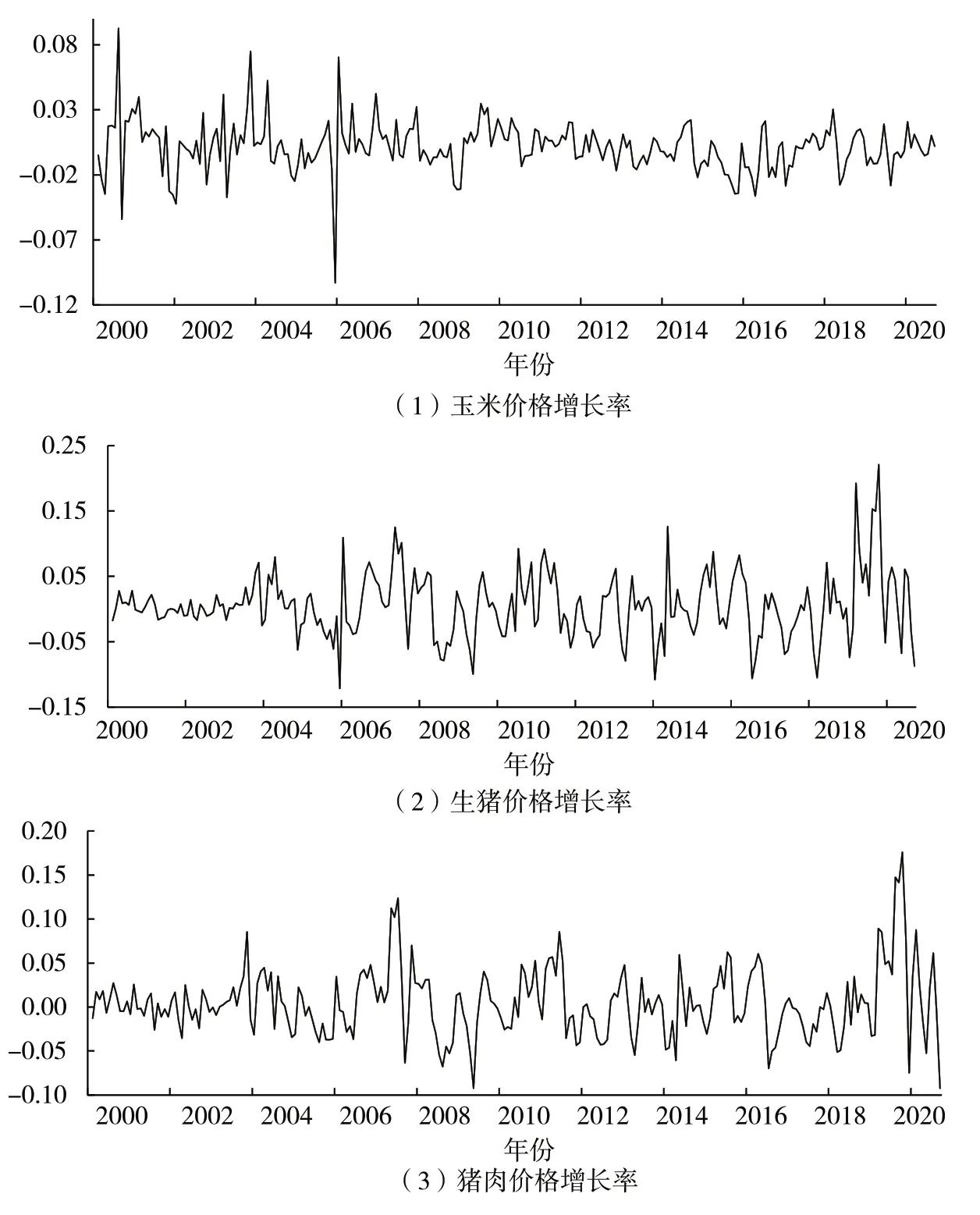
图2 2000—2020年玉米、生猪和猪肉价格增长率动态走势

表1列出了玉米、生猪和猪肉价格增长率序列的描述性统计特征。首先，从均值来看，玉米价格增长率均值为0.001，然而生猪、猪肉价格增长率均值为0.005，表明生猪和猪肉价格增长的平均速度要快于玉米价格。其次，从标准差来看，生猪价格增长率的标准差最大，其次是猪肉、最后是玉米，表明生猪和猪肉价格波动相对较高，而玉米价格波动较小，因此生猪和猪肉市场风险明显高于玉米市场。再次，在偏度与峰度方面，玉米、生猪和猪肉价格增长率序列的偏度均大于0，即存在右偏现象，且峰度均在5以上，说明这3种时间序列均具有“尖峰厚尾”的特征。最后，根据JB统计量及其P值可知，玉米、生猪和猪肉价格增长率序列均不服从正态分布。因此，在后续的非对称BEKK-MGARCH模型和DCC-MGARCH模型估计时，均假定残差序列服从Student-t分布。

表1 玉米、生猪和猪肉价格增长率的描述性统计特征

3.2 模型形式选择

首先，运用ADF、DF-GLS和KSPP检验方法对玉米（lpc）、生猪（lph）和猪肉（lpp）价格序列进行单位根检验，检验结果表明lpc、lph和lpp序列中均存在单位根，但是一阶差分后的序列dlpc、dlph和dlpp均是平稳的，因此玉米、生猪和猪肉价格序列均是一阶单整序列。然后，进一步对lpc、lph和lpp序列进行Johansen协整检验，具体结果见表2。

根据表2给出的迹统计量和最大特征根统计量可知，在5%的显著水平上，无法拒绝玉米、生猪和猪肉价格序列之间存在0个协整关系的原假设。由于不存在协整关系，所以基于一阶单整时间序列的VECM模型不适合作为条件均值方程。有鉴于此，该文将包含3个平稳时间序列（玉米、生猪和猪肉价格增长率）的VAR模型作为非对称BEKKMGARCH模型的条件均值方程。最后，还需要确定VAR模型的最优滞后阶数，具体结果见表3。

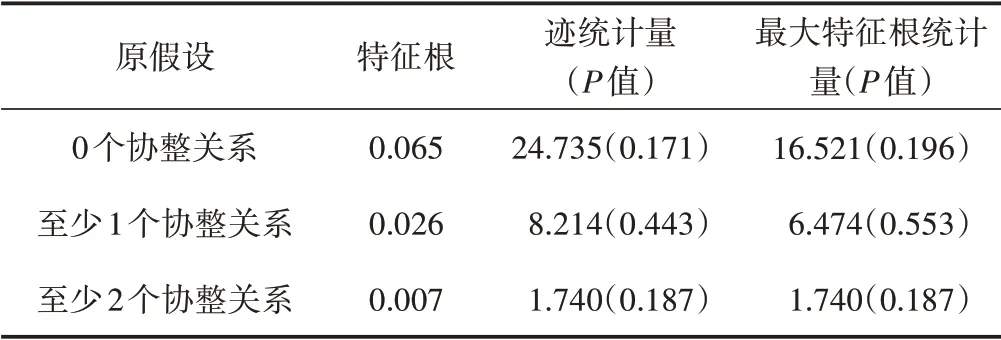
表2 Johansen协整检验

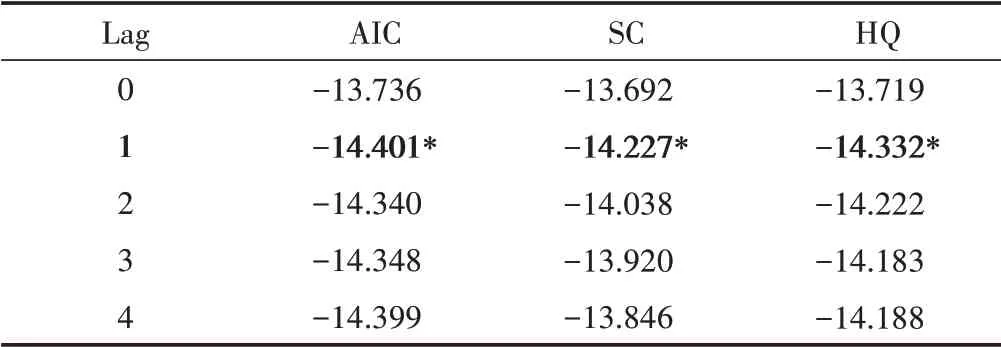
表3 VAR模型最优滞后阶数的确定

根据AIC、BIC和HQ信息准则值可知，VAR模型的最优滞后阶数为1阶，因此选择VAR（1）模型作为非对称BEKK-MGARCH和DCCMGARCH模型的条件均值方程。最后，对VAR（1）模型的残差项进行White异方差检验，检验结果显示卡方统计量值为208.606，在1%的显著水平上拒绝没有异方差的原假设。因此，需要进一步采用非对称BEKK-MGARCH模型和DCCMGARCH模型对VAR模型的残差项进行拟合。

4 结果与分析

4.1 非对称BEKK-MGARCH模型估计与价格波动传导机制分析

该文使用Winrats9.2软件编程，应用BFGS算法估计非对称BEKK-MGARCH模型，经过124次迭代后，模型收敛于0.000 001 6，模型具体估计结果如表4所示。

表4 非对称BEKK-MGARCH模型估计

根据表4可知，标准化残差及其平方项的滞后10阶Ljung-box Q统计量值在5%的显著水平上接受标准化残差及其平方项不存在序列相关的原假设，表明模型的条件均值和条件方差方程设定合理。同时，非对称BEKK-MGARCH模型估计后得到的对数似然函数值为1 891.805，明显高于对称BEKK-MGARCH模型得到的对数似然函数值（1 886.902）①为了节省空间，BEKK-MGARCH模型的估计结果省略，如有需要者，可以向作者索要，而且，反应非对称程度的系数d22和d33在5%的水平上显著。因此，非对称BEKK-MGARCH模型的估计结果优于对称BEKK-MGARCH模型。

基于非对称BEKK-MGARCH模型的估计结果，分析玉米、生猪和猪肉市场之间的价格波动传导机制。其中，矩阵A表示的是ARCH型波动溢出效应，矩阵B表示的是GARCH型波动溢出效应，矩阵D表示的是非对称型波动溢出效应。

（1）分析玉米、生猪和猪肉市场自身的波动溢出效应。对于玉米市场来说，反应ARCH和GARCH型波动溢出效应的参数a11和b11均在5%的水平上显著，但是反应非对称型波动溢出效应的参数d22在5%的水平上不显著，说明玉米价格增长率的波动具有持续性特征，而且对新息冲击存在着显著的反应，但是对于正向和负向冲击的反应是对称的。对于生猪和猪肉市场来说，参数a22，b22和d22分别在1%、1%和5%的水平上显著，参数a33、b33和d33也均在1%、10%和1%的水平上显著，表明生猪和猪肉市场都存在着显著ARCH、GARCH和非对称型波动溢出效应。因此，生猪和猪肉价格增长率的波动会表现出较强的持续性，同时面对负向冲击的反应会显著高于面对正向冲击的反应。综上所述，相对于玉米市场来说，生猪和猪肉市场表现出更大的市场价格波动风险。因此，建立生猪和猪肉市场风险预警机制，加强对疫病等负向冲击的关注和应对能力，对保持生猪和猪肉市场价格稳定具有重要意义。

（2）分析玉米、生猪和猪肉市场之间的波动溢出效应。对于玉米和生猪市场来说，由于参数a12、b12和d12估计值在5%的水平上不显著，因此玉米市场对生猪市场没有波动溢出效应；反过来，系数a21在1%的水平上显著，但是b21和d21在5%的水平上不显著，说明玉米和生猪市场之间，仅存在着生猪市场对玉米市场单向ARCH型波动溢出效应，而且波动溢出效应不存在非对称性特征。对于玉米和猪肉市场来说，由于参数a13、b13、和a31估计值分别在在5%、10%和1%水平上显著，说明玉米市场对猪肉市场存在着ARCH和GARCH型波动溢出效应，反过来，猪肉市场对玉米市场存在着ARCH型波动溢出效应，即玉米和猪肉市场之间存在着双向价格波动溢出效应。但是，由于参数d13和d31估计值在5%的水平上均不显著，因此玉米和猪肉市场之间不存在非对称型波动溢出效应。对于生猪和猪肉上来说，由于参数a23、b23和b32在1%的水平上显著，表明生猪市场对猪肉市场存在着ARCH和GARCH型波动溢出效应，猪肉市场对生猪市场存在着GARCH型波动溢出效应，即生猪和猪肉市场之间存在着双向价格波动溢出效应。图3归纳总结玉米、生猪和猪肉市场之间的价格波动溢出效应，横线上标明了价格波动溢出效应的类型，箭头表示价格波动传导的方向。

从图3中可以看出，玉米（生猪）市场与猪肉市场之间存在着双向价格波动溢出效应，说明猪肉市场同时受到来自玉米和生猪两个市场价格波动和新息冲击的影响；反过来，猪肉市场的价格波动又会传导到玉米和生猪市场，因此稳定猪肉市场价格波动的关键在于稳定玉米和生猪市场价格波动。因此，借助于饲料成本“保险+期货”模式稳定玉米价格，从而实现稳定猪肉价格的政策目标是有实践依据的。另外，由于中国在2021年初已经推出生猪期货，为生猪市场“保险+期货”模式①生猪期货的推出为生猪饲养者提供了套期保值的工具，但是中国生猪年出栏数量在1～49的养殖户仍然占到94.6%（《中国畜牧兽医年鉴》，2018年），这些散户由于缺乏必要的期货投资知识和意识，因此直接参与期货市场交易的可能性较低。有鉴于此，生猪“保险+期货”模式会是生猪养殖户和猪肉销售商规避市场风险的主要方法与手段，生猪饲养者可以利用生猪“保险+期货”模式来稳定预期收入，猪肉销售商可以利用生猪“保险+期货”模式稳定生猪价格，通过稳定成本来获取预期收入的应用提供了实践基础，因此对于同时具有生猪养殖和猪肉销售业务的企业来说，同时利用玉米和生猪价格“保险+期货”模式可以显著提升“保险+期货”模式稳定猪肉市场价格波动的效果。

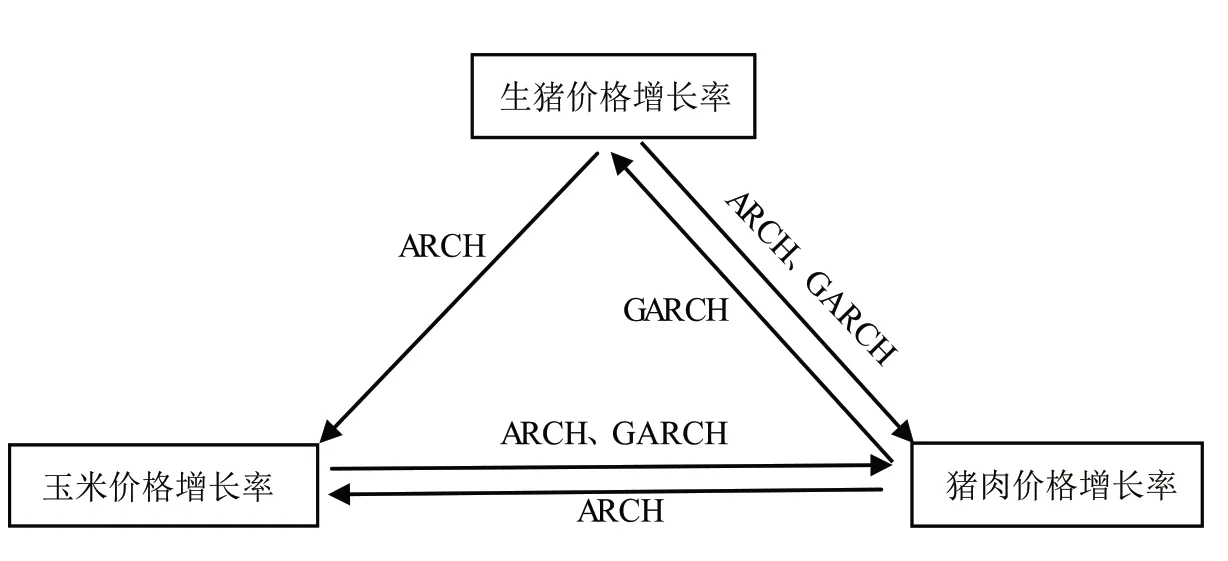
图3 玉米、生猪和猪肉市场之间的价格波动溢出效应

（3）玉米市场同时受到来自生猪和猪肉市场上新息冲击（例如：突发疫情、政策调整等）的影响。虽然生猪市场仅受到来自猪肉市场价格波动的影响，但是玉米市场也可以借助于猪肉市场间接地影响生猪市场价格波动。因此，当政府制定玉米、生猪和猪肉市场价格调控政策时，或者当玉米种植者、生猪养殖者以及猪肉经销商制定生产决策时，应该基于整个生猪产业链制定，并且考虑产业链上不同市场之间价格波动溢出效应对政策实施效果的影响。

图4和表5分别给出了玉米、生猪和猪肉价格增长率序列的条件方差及其描述性统计特征。由于条件方差可以测度价格波动水平，因此条件方差序列是可以反映不同市场风险的指标。由表5可知生猪市场价格波动幅度最大，条件方差的平均值和标准差分别为0.041和0.018，高于猪肉市场（均值和标准差分别为0.029和0.014）和玉米市场（均值和标准差分别为0.018和0.009），表明生猪市场风险最高，其次是猪肉市场，最后是玉米市场。从图4中可以看出，玉米价格增长率在临时储备政策实施期内的波动水平最小，而在政策实施前后，波动水平明显提高，尤其是在政策实施前，玉米价格增长的波动水平高于生猪和猪肉价格增长率的波动水平。由此可见，玉米临时储备政策的实施起到了稳定玉米价格波动的作用。2016年开始，中国取消玉米临时储备政策，随着玉米价格市场化改革的深化，玉米价格波动水平也逐步提高。

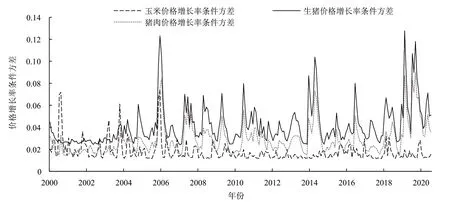
图4 2000—2020年玉米、生猪和猪肉价格增长率条件方差序列走势

表5 玉米、生猪和猪肉价格增长率条件方差的描述性统计特征

4.2 DCC-MGARCH模型估计与市场动态相关性分析

为了更加深入的理解玉米、生猪和猪肉市场之间的动态关联度，该文进一步应用DCC-MGARCH①该文对非对称DCC-MGRACH模型进行了估计，但是估计结果表明反应不同市场之间非对称价格波动溢出效应的参数并不显著，该结论与非对称BEKK-MGARCH模型估计结果相吻合。非对称BEKK-MGARCH模型估计结果也表明非对称波动溢出效应仅存在于生猪或猪肉市场中，然而在不同市场之间并不存在着非对称价格波动溢出效应见图3模型检验玉米、生猪和猪肉市场之间的动态相关关系，考察期不同市场之间相关性的时变特征。

表6给出了DCC(1,1)-MGARCH模型的参数估计结果。从表6可以看出，αi，βi均在5%的水平上显著，α在10%水平上显著，而且αi+βi＜1，α+β＜1，均符合Engle[36]给出的约束条件，因此模型设定较为合理。

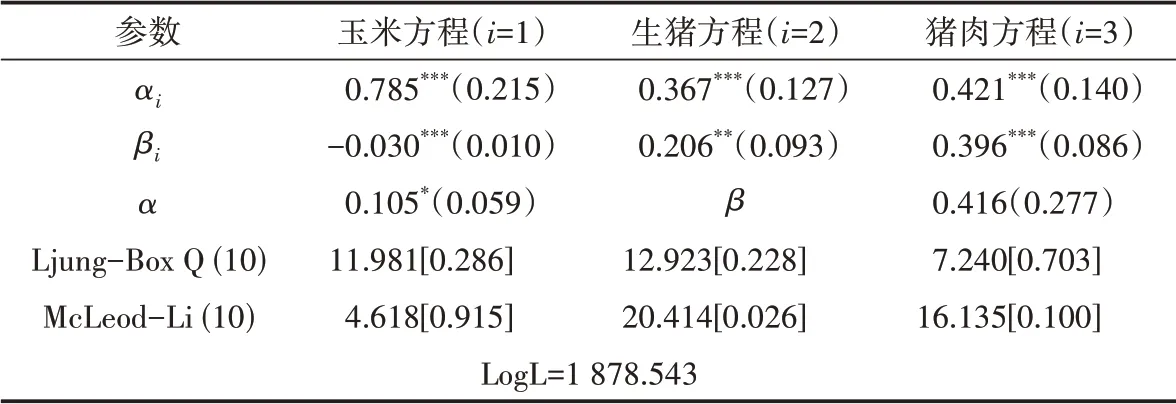
表6 DCC(1,1)-MGARCH模型估计

图5和表7分别给出了玉米、生猪和猪肉市场之间的动态相关系数及其描述性统计特征。从中可以看出生猪和猪肉市场动态条件相关系数大体上稳定在0.892左右，表明生猪和猪肉市场之间的关联程度非常高，因此针对于某一市场制定的价格稳定政策也会起到降低另一个市场价格波动的效果。再者，从整个样本起来看，玉米和生猪（猪肉）市场之间呈显著正相关关系，这就意味着稳定玉米市场价格波动水平有助于稳定生猪（猪肉）市场价格波动水平。因此，饲料成本“保险+期货”模式具有稳定猪肉市场价格的效果，该结论与非对称BEKK-MGARCH模型的结论相一致。但是，由于玉米和生猪（猪肉）市场之间动态相关系数较低，平均值仅为0.092（0.128）。因此，饲料成本“保险+期货”模式的作用效果并不会很显著。

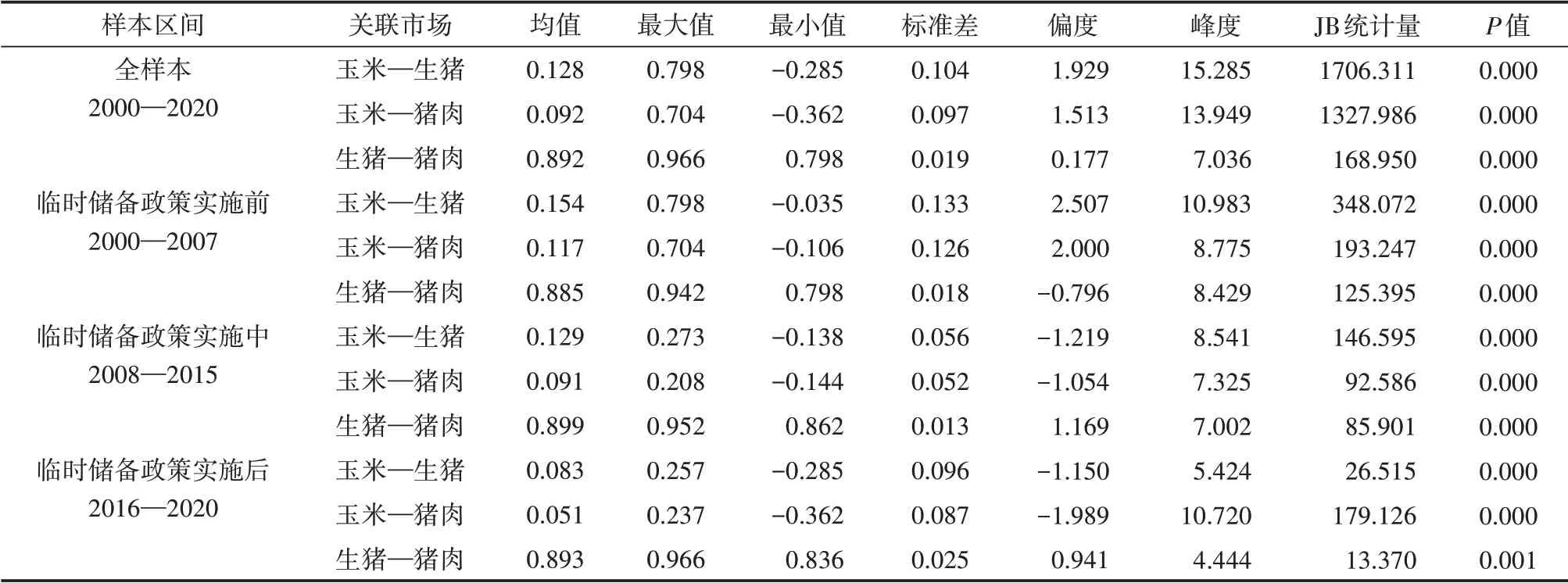
表7 动态条件相关系数的描述性统计特征

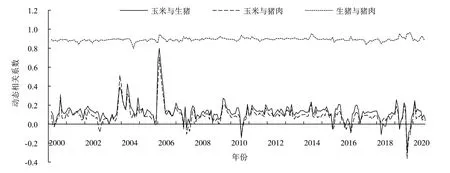
图5 2000—2020年玉米、生猪和猪肉价格增长率序列之间的动态条件相关系

再者，玉米、生猪和猪肉市场之间的动态相关关系是不稳定的，这可能与玉米市场频繁的政策转变密切相关。该文根据玉米市场的政策变化将样本期划分为3个阶段：第一段为玉米临时储备政策实施前（2000—2007年），第二阶段为玉米临时储备政策实施中（2008—2015年），第三阶段玉米临时储备政策实施后（2016—2020年）。

在第一段中，由于玉米价格市场化程度较高，玉米价格的变动是市场供需关系的反应，因此玉米和生猪（猪肉）市场之间表现出较高的市场关联度，尤其是2004—2006年，动态相关系数的最高值可达0.798（0.704），这段时间正好是生猪和猪肉价格快速上升和下降的时期（如图1），由此可以推断玉米价格的剧烈波动确实是导致生猪（猪肉）市场价格异常波动的重要原因。这就意味着，如果能稳定玉米价格，那么生猪（猪肉）市场价格波动水平也会随之降低。因此，在玉米价格市场化程度较高的时期，饲料成本“保险+期货”模式的实施效果应该是非常显著的。

在第二阶段中，玉米临时储备政策的实施降低了玉米价格的市场化水平，导致玉米市场和生猪（猪肉）市场之间的动态相关系数显著降低，动态相关系数的最高值仅为0.273（0.208）。这就表明玉米临时储备政策的实施在很大程度上降低了玉米市场与生猪（猪肉）市场之间的动态关联度。因此，在玉米价格受到政府管制时，应用饲料成本“保险+期货”模式来稳定猪肉市场价格的政策效果就会大幅减弱。

在第三阶段中，政府取消了玉米临时储备政策，玉米价格市场化程度不断提升，但是玉米市场与生猪（猪肉）市场之间的动态相关系数并没有显著提升，反而在短期内还出现过负相关关系，这主要是由于2016年玉米市场政策改革、2018年非洲猪瘟爆发、2019年中美贸易战以及2020年新冠疫情等外界冲击导致的短期异常现象。由此可见，重大外界冲击也会降低玉米、生猪和猪肉市场之间的关联程度，从而限制了饲料成本“保险+期货”模式的实施效果。根据供需理论和第一阶段的经验分析，可以预期随着玉米价格市场化改革的深入以及外界冲击影响的逐步减弱，玉米与生猪（猪肉）市场之间的动态相关系系数会逐步提升，使得饲料成本“保险+期货”模式的实施效果更加明显。

5 主要结论与政策启示

5.1 主要结论

该文应用非对称BEKK-MGARCH和DCC-MGARCH模型研究生猪产业链上游玉米市场、中游生猪市场以及下游猪肉市场之间的价格波动传导机制和动态关联程度，进而对饲料成本“保险+期货”模式稳定猪肉价格的效果进行评价，主要结论如下。

（1）非对称BEKK-MGARCH模型估计结果表明生猪和猪肉市场受到负向冲击的反应显著高于正向冲击的反应，即存在非对称波动溢出效应，因此采用非对称BEKK-MGARCH模型是合理的。这也表明生产者、销售者以及政府等生猪产业利益主体应该更加注重生猪和猪肉市场的疫病、消费疲软等负向冲击的影响，及时采取措施应对负向冲击给生猪产业带来的较大风险。

（2）玉米（生猪）市场与猪肉市场之间存在着双向价格波动溢出效应。其中，玉米（生猪）市场对猪肉市场同时存在着GARCH和ARCH型波动溢出效应，这就意味着在短期内玉米（生猪）市场上的政策、疫病等外界冲击会增加猪肉市场价格波动水平；从长期来看，玉米（生猪）市场上一期的价格波动也会传导到当期猪肉市场。因此，使用饲料成本“保险+期货”模式，通过稳定玉米价格可以起到降低猪肉市场价格波动的效果。

（3）DCC-MGARCH模型估计结果表明玉米和生猪（猪肉）市场之间呈显著正相关关系，这就意味着稳定玉米市场价格波动水平有助于稳定生猪（猪肉）市场价格波动水平。因此，饲料成本“保险+期货”模式具有稳定猪肉市场价格的效果，该结论与非对称BEKK-MGARCH模型的结论相一致。但是，由于玉米和生猪（猪肉）市场之间动态相关系数较低，平均值仅为0.092（0.128），因此，饲料成本“保险+期货”模式的作用效果并不会很显著。

（4）玉米临时收储政策降低了玉米市场与生猪（猪肉）市场之间的关联度，在政策实施前，玉米与生猪（猪肉）市场之间的动态相关系数显著高于政策实施过程中的动态相关系数，尤其是2004—2006年，动态相关系数最高，这段时间正好是生猪和猪肉价格出现大幅波动的时期，因此玉米价格市场化水平较高时，玉米价格波动是推动生猪（猪肉）价格波动的重要原因。在玉米临时储备政策结束后，虽然玉米价格市场化水平提升，但是由于受到非洲猪瘟、中美贸易战和新冠肺炎疫情等众多外界冲击的影响，玉米、生猪和猪肉市场之间的动态相关系数并没有提高。综上，饲料成本“保险+期货”模式稳定猪肉市场价格的效果会受到玉米市场政策和重大外界冲击的影响。

5.2 政策启示

由于价格波动传导与风险管理密切相关，而风险管理是影响农产品产业链上各个环节价格稳定的重要因素。因此，农产品产业链上价格波动传导机制的研究可以为政策制定与风险规避提供重要的决策信息。

（1）从政策制定视角。首先，继续保持和深入玉米市场改革，提升应对重大外界冲击的能力有助于提高饲料成本“保险+期货”模式稳定猪肉市场价格波动的作用效果。具体建议如下：减少对玉米市场不必要的政策干预，让玉米价格更多地体现供需关系的变动；建立重大疫情、贸易冲突等突发事件的应急策略和应对机制。其次，在制定和实施猪肉收储等价格调控政策时，要充分考虑生猪产业链上各环节之间的价格波动传导机制，尽量基于整个生猪产业链，而非个别环节制定价格调控政策。

（2）从风险规避视角。首先，掌握生猪产业链上价格波动传导机制有助于玉米种植者、生猪饲养者、猪肉销售商以及玉米、生猪等期货投资者预期玉米、生猪和猪肉价格走势，从而提高生产和投资决策的科学性和准确性。另外，由于缺乏猪肉期货交易市场，猪肉销售商可以通过投资与其密切相关的玉米和生猪期货市场来实现自身价格的稳定；对于缺乏期货投资知识的猪肉销售商，则可以利用“保险+期货”模式，借助具有专业知识的期货和保险公司来实现自身价格的稳定。

以上政策建议是针对于猪肉市场提出的，但是也同样适用于其他农产品市场。2016—2021年连续6年的“中央一号文件”都着重强调要积极推行重要农产品“保险+期货”模式，“保险+期货”模式将会成为农产品市场风险控制的重要手段，上述研究成果为饲料成本“保险+期货”模式等市场风险调控政策的制定与实施提供了理论和实践依据，即缺乏风险规避工具（期货、保险等）的农产品市场可以利用关联市场上的风险规避工具，来间接实现自身价格的稳定。