多粒子碰撞动力学方法在计算物理教学中的应用

刘心爽 张超越

（安庆师范大学物理系，安徽 安庆 246133）

0 引言

计算物理是运用计算机作为工具，通过数值计算、数据处理、模拟仿真等手段解决复杂物理问题的一门应用科学。计算物理可以处理理论物理无解析解问题，同时也可以处理实验物理上因实验条件限制而不能处理的问题。近些年来，随着计算机技术的快速发展和学科间的进一步渗透，计算物理得以蓬勃发展，计算物理也成为国内高校物理学及相关专业本科生的专业课程。

目前国内计算物理教学主要集中在运用计算软件（通常为Matlab）指令库进行数值微分与数值积分、解常微分方程、解偏微分方程以及一些数值模拟方法（如蒙特卡罗方法）[1，2]。计算物理教学的特点是学科间交叉性强，能够在一定程度上帮助学生对线性代数、插值、非线性方程组和计算机编程等一系列知识的掌握，同时，能够很好地培养学生解决问题的能力，可见计算物理在本科教学中的重要性。

然而，在传统计算物理教学中存在着一些不足。首先，教学方式单一。传统教学中采取教师到学生的“单向传授”教学模式，并不适宜于计算物理的教学。其次，教学内容前沿性不足。目前的计算物理教学主要集中在运用数值方法求解典型的物理问题，帮助学生掌握数值处理方法及方程解法，同时提升编程能力。但是，学生对计算物理的发展和前沿领域知之甚少，特别是对物理、化学、生物、计算机等多学科的交叉研究领域和新兴发展的研究方法。为了拓宽学生的视野，为了改进诸如此类的传统计算物理教学上的不足、激发学生在计算物理学习中的积极性与主动性、培养学生的科学思维、发挥学生的主体性并提高有效解决实际问题的能力、开拓学生的视野从而帮助学生更加深入了解计算物理这门课程，笔者将多粒子碰撞动力学方法引入计算物理的教学之中，以此在教学过程中进行补充说明，提高课堂教学效果，从而满足课堂教学效果。

多粒子碰撞动力学（Multi-particle Collision Dynamics：MPCD）方法是一门新兴的计算方法，由Malevanets和Kapral于1999年提出，又被称为随机旋转动力学，广泛用于软物质体系的动力学模拟研究[3-5]。在软物质系统的研究中，复杂的溶剂环境是研究过程中面临的一个重要的问题，如胶体凝胶粒子系统，粒子间除了存在静电作用力以及分子间作用力和体积排斥作用外，还存在着长程流体力学作用（Hydrodynamic Interaction，HI）[6]。这种长程的相互作用是由溶剂环境所产生的，并伴随着粒子运动的始终。由此可见，流体力学效应对系统动力学行为的影响是一直存在的，应该被考虑进来。而在很多时候，为了简化动力学过程，通常会忽略流体力学效应，将环境的影响用噪声项来替代。多粒子碰撞动力学方法能很好地解决这个问题。

1 粒子碰撞动力学方法的基本原理

在多粒子碰撞动力学方法中，为了考虑溶剂效应，同时又不会因粒子数的提高在很大程度上提高计算量，溶剂分子被抽象成粒子间无体积排斥的点状粒子，粒子以连续的速度分布在连续空间运动。MPCD模拟方法中，体系的动力学演化过程分为粒子位置演化和速度演化两步，笔者分别称之为粒子的流动和粒子的碰撞。

1.1 粒子流动

在t时刻，粒子t的位置为ri（t），速度为vi（t），经过ΔtMPC时间后粒子的位置更新为：

进而遍历系统中所有粒子。

1.2 粒子碰撞

由于粒子被抽象成点状粒子，粒子间无相互作用力，为了实现粒子间的动量交换，在MPCD方法中采用了一种粗粒化的碰撞处理操作。具体来说，首先将系统分割成一系列网格并做好编号，系统中粒子划分到具体网格中，同一网格中的粒子间相互碰撞交换动量，不同网格间粒子之间互不干扰不进行动量交换。在模拟过程中，通常选定常数作为网格的边长，网格中粒子平均数目M∈[3，20]。在实际碰撞过程中，由于每次进出格子的粒子数目并不一定相等，因而网格中真实的粒子数目Nc并不固定，存在一定涨落，一般在平均值M附近波动，其原因是粒子在碰撞后进入邻近格子之中。在t时刻，由碰撞网格ξ中所有粒子的瞬时速度vi可计算出网格的质心速度vξcm=t），则在t+ΔtMPC时刻粒子的速度大小为：

式中：δvi（t）=vi（t）-vξcm（t）为粒子在碰撞过程中速度的变化量。(R为旋转矩阵，在每个时间步长，它将每个单元格的速度围绕随机生成的轴旋转一个角度α。需要注意的是，当溶剂粒子平均自由程λ=ΔtMPCkB为玻尔兹曼常数，T为温度，m为溶剂粒子质量）相对网格尺寸比较小时，粒子需要经过反复的碰撞才会进入或者流出网格，这种反复的碰撞会使得粒子间的时间关联加强，导致伽利略不变性被破坏。为了保证伽利略不变性，通常在每次碰撞之前对网格进行一次随机移动，这样粒子会重新划分格子，与新的格子中的粒子进行碰撞，碰撞结束后格子再移动回来。这种移动网格的方式，既可以保证伽利略不变性，还可以加速动量在格子间的传递。当λ的值大于a0/2时，不需要移动网格。

在MPCD算法中，通过粒子流动和碰撞步的交替演化，粒子之间实现了动量的传递，同时每个格子中的动量和能量守恒，因而体系可以通过溶剂产生流体力学相互作用，进而通过此方法可以模拟体系中的流体力学。

当系统中除了溶剂粒子外，还存在溶质粒子（包括胶体粒子、纳米粒子、高分子链等）时，特别是需要研究溶剂的流体力学效应对溶质的动力学行为影响时，需要在溶质和溶剂间建立相互作用关系，溶质粒子与溶剂粒子间需要进行耦合。为了实现溶质与溶剂间耦合，Kapral等提出了多粒子碰撞结合粗粒化分子动力学（MD-MPCD）的方法。在该方法中，溶质与溶剂的动力学演化过程是分开的，溶质粒子采用分子动力学进行演化，而溶剂粒子采用上面介绍的流动-碰撞交替的方式进行，这种方式有效地避免了由溶剂粒子数目产生的分子动力学的计算，极大地节约了计算成本。需要注意的是ΔtMD＜＜ΔtMPC，也就是说，在动力学模拟过程中，当溶质粒子进行多次分子动力学演化后，溶剂分子才进行一次演化。对于溶剂和溶质间的耦合，通常采用碰撞耦合的方式，在该过程中，和溶剂粒子一样，溶质粒子也被视为点状粒子，动量交换过程中溶质和溶剂共同参与碰撞。具体说来就是，在碰撞步前，同时将溶质粒子和溶剂粒子视为点状粒子划分到网格之中，当网格ξ中含有Nc个质量为m的溶剂粒子和Nm个质量为M的粒子时，网格的质心速度为其中，vi和Vj分别为第i号溶剂粒子和第j号溶质粒子的速度。碰撞时，按照公式（2）的碰撞方式，溶质粒子和溶剂粒子随机碰撞，从而实现溶质和溶剂间动量交换，进而达到溶质和溶剂耦合的效果。该方法相比于相互作用力耦合和热边界耦合简单实用，已被广泛应用于软物质系统。

2 多粒子碰撞动力学方法的应用

作为一个具体例子，首先运用多粒子碰撞动力学模拟了二维泊肃叶流，再将高分子链置于二维泊肃叶流中。如图1所示，在x方向选取Lx=100a0，满足周期边界条件，y方向两平板间距设定为Ly=30a0。当流体粒子在x方向受到重力场g驱动时，由于在边界处（y=0和y=Ly），流体粒子与边界的摩擦效应使得沿x方向速度vx减小为零，而在两平行板中心，vx取得最大值。两平行板间流场形成抛物形的轮廓线，理论上满足v（xy）=Ly-y）y，其中，η为流体粘滞系数，g为施加在流体上的力产生的加速度大小。

图1 泊肃叶流场示意图

在模拟过程中，溶剂粒子和平行板之间采用无滑边界。模拟结果如图2所示，在不同的驱动力作用下，在边界处流场速度趋向于0，在平行板中间位置流体速度达到最大值，这与理论上保持一致。模拟中，逐渐增大重力场大小0.000 5、0.00 1、0.001 5，发现单调上升，三条曲线对应的最大值分别为0.044 9、0.090 6、0.133 1，值的大小比例与保持一致。实际中，通过模拟流体在管道中的速度场，可以运用理论公式间接的测量流体黏滞系数，这里就不做过多陈述。

图2 不同驱动力作用下泊肃叶流场平均速度轮廓线（自上而下g=0.000 5、0.00 1、0.001 5）

当该系统中含有溶质粒子时（如高分子链），在通道中，高分子链在泊肃叶流的驱动下将沿着流体的驱动方向运动，高分子链采用链—珠模型，临近高分子链单体之间通过有限张伸非线性弹性势（FENE）连接。

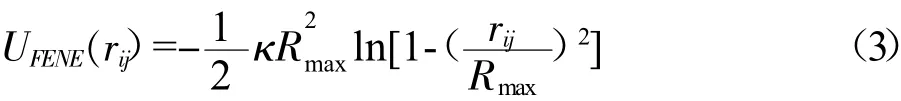
式中：k是弹性耦合常数，Rmax表示键长，即高分子链单体间所能允许的最远距离。高分子链单体之间的即体积排斥作用通过WCA（Weeks-Chandler-Andersen）势表示。

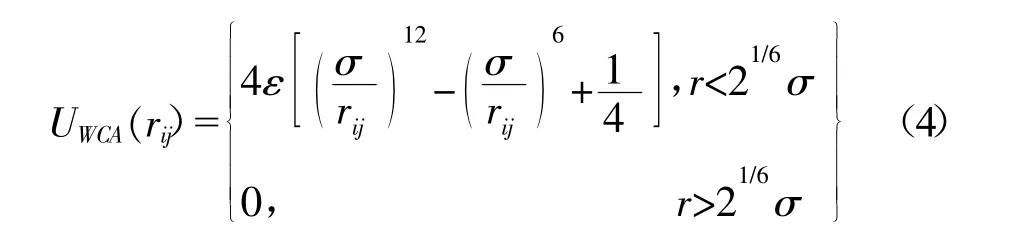
式中：ε表示势能的强度大小；σ为高分子链单体直径；rij为任意两单体之间的距离。关于高分子链，采用标准的分子动力学进行演化。

根据Verlet算法求解（5）式牛顿运动方程为：

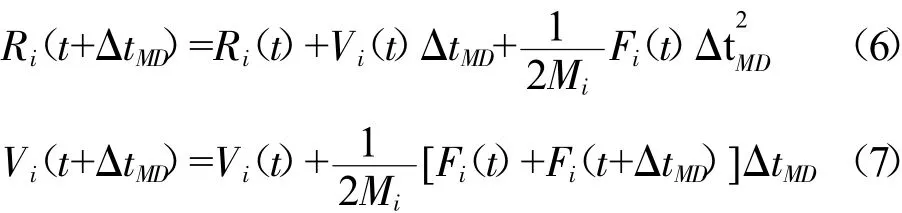
式中，Ri（t）、Vi（t）、Fi（t）分别为i号溶质粒子的位置、速度、所受力。溶质与溶剂耦合时，溶质和溶剂之间相互碰撞并交换动量。

笔者研究了高分子链在平行板管道中的密度分布，如图3所示，横坐标为管道宽度，纵坐标为高分子链的分布。观察到，高分子链主要分布在管道中间，很难在管道壁中长时间停留，在边界处的分布趋向于零。有趣的是，高分子链在管道中的密度分布不是呈现单峰分布的，在管道中间位置的分布不是最多，在管道中心的附近呈现双峰分布。

图3 高分子链在管道中的密度分布

将这些偏离中心的峰值归因于相互竞争的迁移效应。其一，二维系统中泊肃叶流的速度分布是抛物形的，中间快两边慢，这种剪切的速度梯度在很大程度上影响高分子链的构型（受到高剪切速率的高分子会被拉伸的更多），使得高分子链活性产生一个运动梯度（高分子链扩散）。根据动力学理论，高分子链扩散率的梯度会导致链迁移，并且链迁移的方向是远离泊肃叶流的通道中心[7]。其二，热扩散和流体力学效应使得高分子链向管道中间运动[8]。正是由于这两种效应的相互竞争，使得高分子链在管道中的分布呈现有趣的双峰分布。

3 结语

针对安庆师范大学物理学专业教学的实际情况，对计算物理教学内容进行了改进完善。在教学中引入多粒子碰撞动力学方法的介绍，并结合具体例子—泊肃叶流的产生来说明该方法的实际应用。通过模拟泊肃叶流流场分布以及流场中高分子链的分布来刻画流体力学效应。“多粒子碰撞动力学”这一新兴方法的引入，将对构建更加完整的计算物理教学体系发挥重要的作用。更重要的是极大地拓展了学生的知识面和认知，深化了学生从介观体系对统计物理问题的理解，激发了学生对新事物的好奇心，培养了学生的科学思维，充分体现了教学中学生为中心的主线和持续改进的理念。