基于CFD三维集成电路微通道传热特性分析

江美霞，龚俭龙

（1.广州城市职业学院，广东 广州 510405；2.广东交通职业技术学院，广东 广州 510800）

1 前言

随着半导体的技术已进入纳米量级，三维集成电路(3D IC)由多个硅芯片的垂直堆叠而成。与二维集成电路（2D IC）相比，3D IC具有更好的性能和更高的系统集成。然而，3D IC单位体积内电路的功率密度越来越大，这将大大提高集成电路内部器件的工作温度，芯片内部过高的温度梯度产生的热应力将导致有源层器件的稳定性和可靠性下降，甚至出现电子迁移效应和热衰竭，这将给芯片带来严重的性能下降的问题，从而使得3D IC的热管理问题变得异常严峻。

3D IC的散热问题需高效的冷却技术来改善。微通道散热器具有高效的冷却性能和高密封装的优点，自Tuckerman等人首次提出微通道散热器以来受到很多关注，并在3D IC热优化设计中得到了广泛的应用。在层与层之间通过液体在微通道中流动，在流动的过程中带走了芯片产生的热量，从而达到了3D IC散热的目的。Sasaki等人研究了不同压降下微通道的宽度和高度对传热性能的影响。Peng等人研究了矩形微通道中的水力直径和通道纵横比对摩擦系数和传热有很大影响，研究结果表明，通过改变流道的结构可以优化微通道的散热性能。Kuppusamy等人研究了梯形槽和三角形槽对微通道散热器性能的影响。实验结果表明，与梯形槽的微通道相比，三角形槽可以产生更大的漩涡，有着更好的传热性能。

本文以三维集成电路单层不同形状的横截面的微通道热沉为研究对象，利用三维软件Solidworks分别建立三维集成电路的圆形横截面的微通道和矩形横截面的微通道模型，再通过CFD软件对三维集成电路中矩形横截面的微通道和圆形横截面的微通的传热性能进行数值仿真分析，从而得出较优的三维集成电路的微通道热沉结构。

2 基本理论

2.1 CFD研究方法

计算流体动力学（CFD）是通过数值方法求解流体与气体动力学基本控制方程的学科。CFD软件是一种可用于流体场分析、流体场计算、流体场预测的软件。通过CFD软件数值模拟可以更加深刻理解问题产生的机理，在较短的时间内预测到模拟对象的相关性能，通过优化各种参数，使得设计效果到达最优，为产品开发提供指导，节省了开发成本，缩短了开发周期。

CFD软件主要有三种功能，分别为前段处理、计算和结果数据生成、后处理。CFD求解问题的基本思路如图1所示。

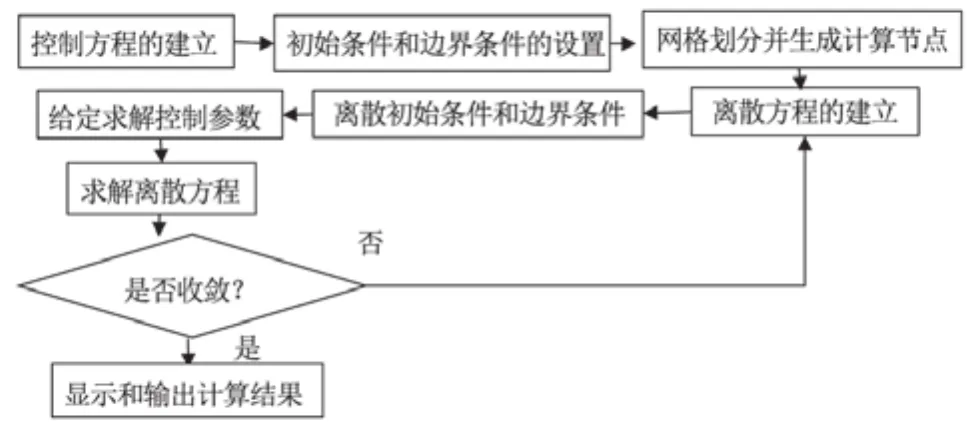
图1 CFD求解问题的基本思路

2.2 传热理论

三维集成电路热设计中应用了传热学基本理论。在传热学基本理论中，热量传递的基本方式有3种，分别为热传导、热对流、热辐射。热传导是基于物体各部分之间不发生相对位移时，依靠分子、原子及自由电子等微观粒子的热运动而产生的热量传递。热对流是由于流体（气体或者液体）内部各部分的温度不同而造成的相对流动，并与导热是同时存在的。对流传热的机制主要方式有两种，一是强制对流，例如，通过风扇使得流体运动；二是自然对流，例如，流体之间存在温度差而引起流体运动。热辐射是由于热运动产生的，并以电磁波形式传递能量的现象。

3 微通道热沉的模型

3.1 微通道热沉的结构及其描述

本文设计三维集成电路的微通道热沉结构模型为单层平行周期性排列的微通道，共有10个平行通道。微通道分别为圆形横截面和矩形横截面。圆形横截面的微通道的直径为d1=39.9ɥm，圆形横截面的微通道的单元微通道长为L1=160ɥm，宽为W1=160ɥm，高为H1=H2=50ɥm。矩形横截面微通道的单元微通道的边长为d2=100ɥm，d3=50ɥm，矩形横截面的单元微通道长为L2=160ɥm，宽为 W2=160ɥm，高为 H2=50ɥm。为了减少计算时间，在本文中选取了单元微通道作为计算域，单元微通道热沉结构如图2和图3所示。

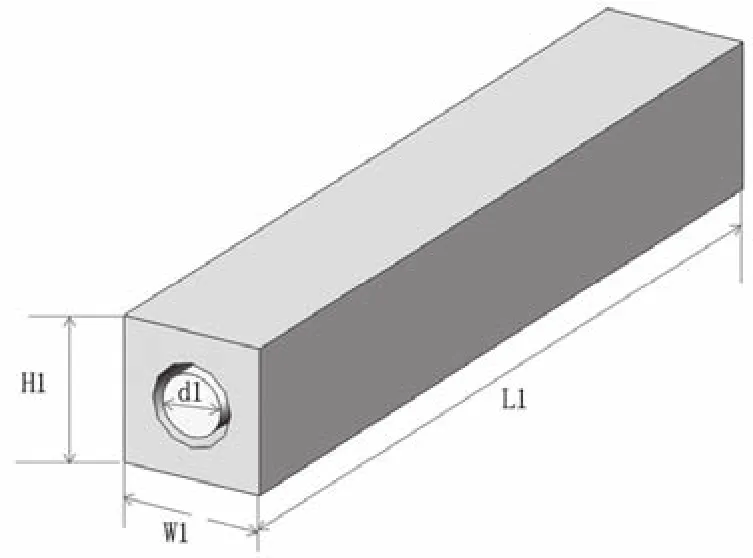
图2 单元圆形横截面微通道

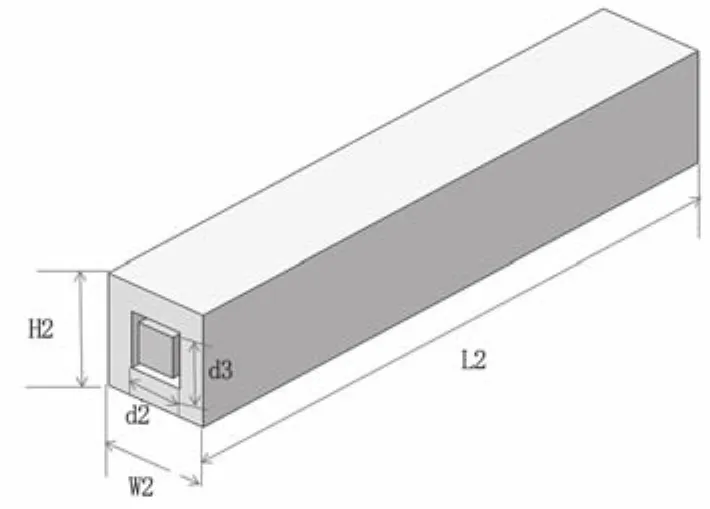
图3 单元矩形横截面微通道

3.2 微通道热沉的建模

本文通过建立三维的流-固耦合模型以求解微通道热沉结构的温度场。为了简化问题，在数值计算过程中，假设如下：冷却流体为单相稳态层流流动；流体和固体的热物理性质不随温度变化，且为不可压缩；忽略重力、浮力及热辐射的影响。

基于上述的假设，三维集成电路中微通道流体的流动和传热过程都需遵循一定的控制方程，其连续性方程、动量守恒方程、能量守恒方程如下：

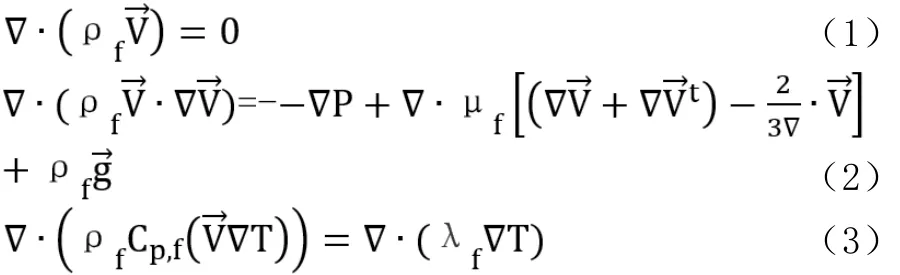
λs为固体导热系数。微通道热沉所有的壁面的边界条件为无滑移边界，进口边界为均匀分布速度进口，入口速度为0.1m/s，微通道中流体的温度300K,出口边界为压力出口，出口面的压强为0Pa，微通道底部加热，热源热流密度为qw=150000W·m-2，其他壁面为绝热。

采用计算流体动力学CFD软件分别求解矩形横截面的微通道和圆形横截面的微通道模型中的层流流动和传热。在计算过程中，采用单相液体水作为冷却液，矩形横截面的微通道和圆形横截面的微通道底面皆以传导传热为主，而流体区域与固体界面皆以对流传热为主。利用SIMPLEC算法来求解速度场和压力场的耦合方程，连续性方程和动量守恒方程采用二阶迎风格式求解。为了提高计算结果的准确性，将连续性方程和动量守恒方程的残差收敛准则小于10-6。

本文在数值计算前对矩形横截面的微通道和圆形横截面的微通道热沉结构的几何模型进行前处理，即网格划分。由于微通道热沉内部结构比较规整，采用六面体网格进行微通道网格划分。

3.3 流体参数

用努塞尔数（Nu）和摩擦阻力系数（f）来表示微通道传热和流动阻力。努塞尔数是一种对流换热强度的无量纲数。

微通道内的努塞尔数定义为：

式中，λf为流体导热系数，Dh为微通道水力直径，h为对流换热系数，定义为：

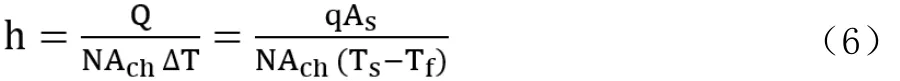
式中，N为微通道的总数，Ach为单个微通道的横截面积，Ts为微通道加热底面的平均温度，Tf为微通道内流体平均温度。

微通道内流体流动的雷诺数表征流体流动情况的无量纲数，定义为：

4 微通道热沉数值仿真分析

利用CFD软件求解，在后处理中可以获得矩形横截面的微通道和圆形横截面的微通道热沉结构的温度场分布云图。从微通道热沉结构的温度场分布云图可以直观反映出微通道热沉温度的变化。矩形横截面的微通道和圆形横截面的微通道内部温度随着流体的流动方向不断吸收热量导致其温度在不断地升高，微通道入口处的温度最低，出口处的温度最高。

圆形横截面的微通道最高温度为22.65℃，如4所示。矩形横截面的微通道最高温度为20.251℃，如图5所示。实验结果表明，不同形状的横截面的微通道有着不同的散热性能，与圆形横截面的微通道相比，矩形横截面的微通道的散热效果较好。

图4 圆形横截面的微通道温度场分布云图

图5 矩形横截面的微通道温度场分布云图

5 结语

本文基于CFD软件，以三维集成电路单层不同形状的横截面的微通道热沉为研究对象，利用三维软件Solidworks 分别建立三维集成电路的圆形横截面的微通道和矩形横截面的微通道模型，采用数值计算方法对圆形横截面的微通道和矩形横截面的微通道模型的传热性能进行数值仿真分析，通过数值仿真的温度场分布云图，直观地获得圆形横截面的微通道和矩形横截面的微通道内流体流动传热特性。实验结果表明，不同形状的横截面的微通道热沉结构对微通道散传热性能有着较为显著的影响，矩形横截面的微通道的传热特性要比圆形横截面的微通道的传热特性好。