不等厚磁极在永磁交流同步伺服电机设计中的分析
2023-01-15魏顺航乔帅翔高晓丽雷莱梁东义
魏顺航,乔帅翔,高晓丽,雷莱,梁东义
(1.郑州电力高等专科学校;2.国网河南超高压公司,河南 郑州 450000)
1 引言
近年来,我国产业结构加快升级,智能制造水平不断提升。在此过程中,永磁交流同步伺服电机以其体积小、效率高、功率密度高、稳定性好等优点在工业机器人、新能源电动汽车、高精度加工机床、航空航天等领域获得了广泛应用。但是,由于永磁电机定子开槽而产生的齿槽转矩在运行中会引起较大的噪音和转矩脉动,影响电机控制精度,难以满足特定场合的使用需求。如何在尽可能不影响永磁电机其他性能的前提下,更好地削弱齿槽转矩,降低转矩脉动,成为当前研究的热点问题。
关于如何削弱永磁电机齿槽转矩,学术界已经有了一定的研究。对于市面上常见的径向磁场永磁电机来说,在电机极槽配比确定的情况下,改变极弧系数、定子斜槽、转子斜极、磁极偏移、采用不等厚磁极、开辅助槽等方法都可以有效地削弱电机齿槽转矩,从而达到降低电机运行时转矩脉动的目的。
但是,其中很多方法要么对于制造加工水平要求较高,不具有大面积推广的经济性;要么会对电机的输出性能、空载反电动势正弦性和径向磁拉力平衡性造成较大的影响,采用之后得不偿失。综合对比来看,在径向磁场永磁交流同步伺服电机中,采用不等厚磁极的方法可以在保证电机输出性能的同时,大大降低齿槽转矩和空载反电动势谐波含量,从而减小转矩脉动,具有很好的研究价值和现实意义。
2 电机结构及参数
2.1 电机主要参数
对于径向磁场永磁交流同步伺服电机来说,定转子铁心由层与层之间相互绝缘的硅钢片沿轴向叠压而成,电机运行时主磁通沿电机的径向平面流通,经过气隙、定子铁心、永磁体、转子铁心等部位形成闭合路径。电机铁心采用硅钢叠片主要是为了切断电机运行时由于磁场交变而在铁心中感生出的涡流电流回路,减小涡流损耗,提高电机运行效率,避免温度过高导致电机损坏。铁心叠压采用的硅钢片厚度越小,截断涡流回路的效果就越好,电机性能会更优异,但相应的成本也会更高。
为更精准地分析不等厚磁极设计对于电机齿槽转矩和转矩脉动的影响,本文以一台额定功率为3.65kW的永磁交流同步伺服电机(以下简称伺服电机)为例,在有限元分析软件中建立瞬态场2D模型并进行仿真计算。伺服电机的转子极数为8,定子槽数为12,额定转速3000r/min,永磁体采用N35SH,主要参数如表1所示。
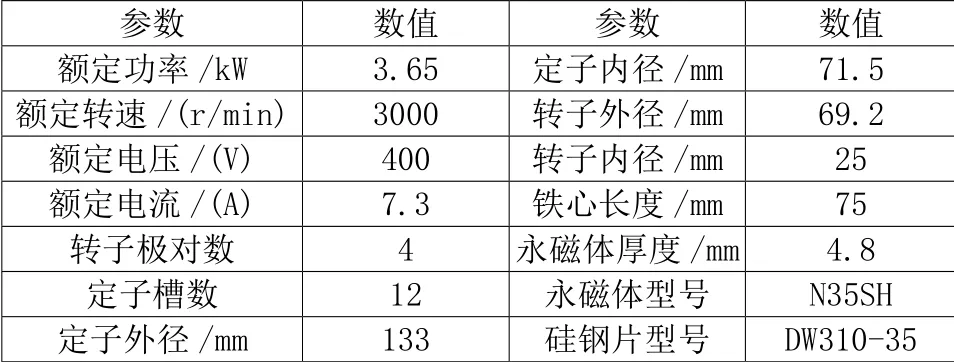
表1 永磁交流同步伺服电机主要参数
2.2 不等厚磁极结构
永磁电机的转子侧采用永磁体励磁,相比于传统的电励磁结构更加简单轻便,可靠性更高,并且由于取消了电励磁铜线绕组,减小了电机铜耗,可以大大提升电机运行效率。普通的径向磁场永磁电机的永磁体表贴在转子表面,磁极厚度均匀,内外径圆心位置相同。
当采用不等厚磁极结构时,永磁体的内、外表面弧度不同,磁极的内外径不同心,磁极外径的圆心为O’,内径的圆心为O,定义O与O’之间的距离为偏心距h,磁极的厚度会随着位置的变化而变化。当改变偏心距h时,就可以调整伺服电机的气隙磁密,从而达到优化电机性能的作用。下文将根据有限元仿真结果分析讨论不等厚磁极对于齿槽转矩和输出性能的影响。不等厚磁极结构如图1所示。
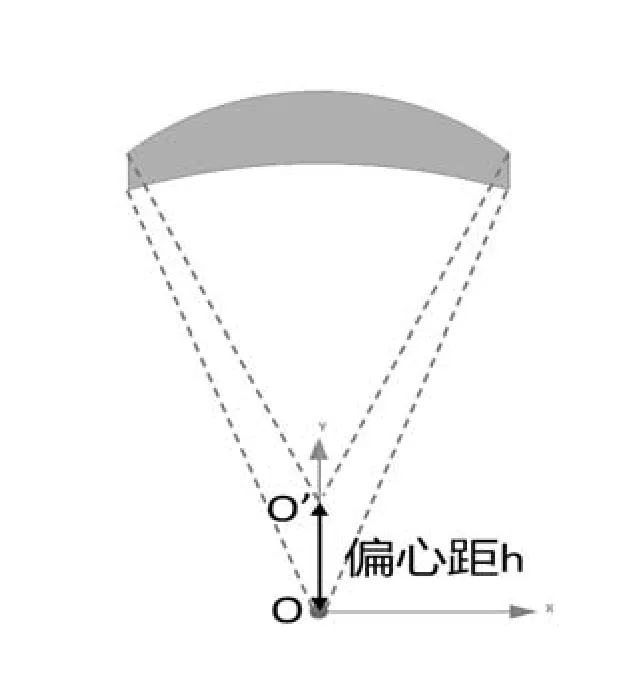
图1 不等厚磁极
3 有限元分析计算
在3000r/min的额定转速下,利用二维有限元仿真软件计算伺服电机不等厚磁极的偏心距h对空载情况下的齿槽转矩、气隙磁密、反电动势以及额定负载情况下的输出转矩的影响。其中偏心距h取值范围为[0,20],取值间隔为5,单位为mm。伺服电机为8极12槽的三相交流永磁同步电机,极槽配比确定后,A、B、C三相定子绕组的空间分布如图2所示。
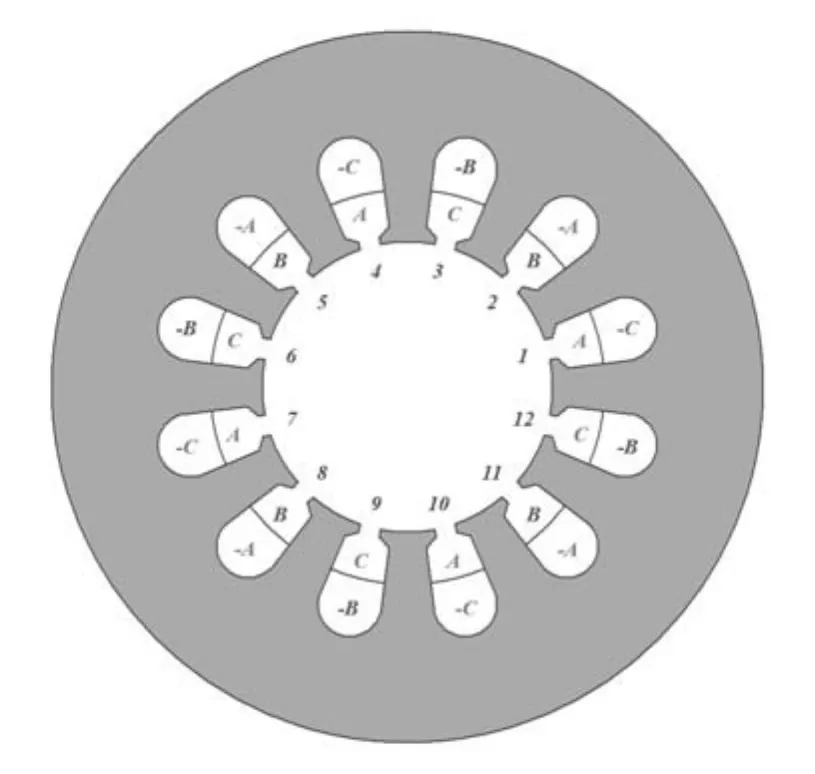
图2 伺服电机定子绕组分布
3.1 空载计算及分析
在3000r/min的额定转速下,分别对伺服电机的齿槽转矩、气隙磁密和反电动势进行仿真计算。得出计算结果如图3至6所示。
图3为空载情况下,偏心距h取不同值时伺服电机的齿槽转矩波形图。图4为齿槽转矩峰峰值随偏心距h的变化趋势图。可以看出,随着偏心距h取值的不断增加,伺服电机的齿槽转矩呈现出明显的下降趋势,h=0mm时的齿槽转矩峰峰值最大,为1.573Nm;h=20mm时的齿槽转矩峰峰值最小,为0.113Nm,相比于最大值下降了92.8%。说明通过改变伺服电机的磁极偏心距,可以极大地削弱齿槽转矩。
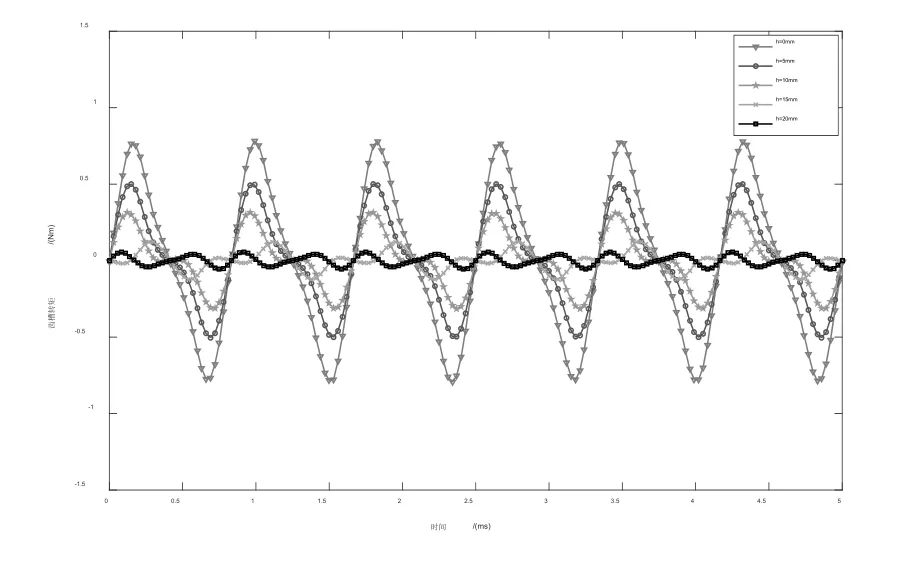
图3 不同偏心距h下的齿槽转矩波形
当然,由图4还可看出,随着偏心距h的增加,齿槽转矩峰峰值的下降速率逐渐放缓。由于伺服电机磁极的永磁体用量会随着偏心距的增加而减少,导致总磁通量下降而引起输出转矩一定程度的降低。因此,在采用不等厚磁极的方法来削弱齿槽转矩时应综合考量,在保证电机输出性能达标的前提下,选取合适的偏心距h的数值以降低齿槽转矩,优化电机转矩脉动。
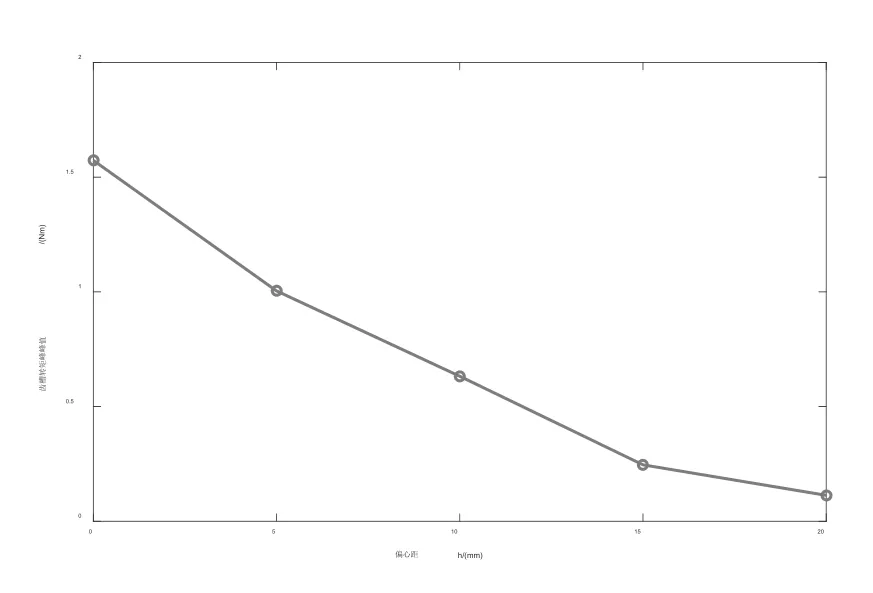
图4 齿槽转矩峰峰值随h变化趋势图
气隙磁密很大程度上可以反应电机的输出性能。在二维有限元空载仿真中,取定转子气隙中部的径向气隙磁密作波形图,不同偏心距h下的空载气隙磁密波形如图5所示。
由图5可以看出,随着偏心距h的增加,空载气隙磁密由平顶波变为尖顶波,波形正弦性有所改善;波形顶部两侧磁密值有下降,气隙磁密有一定的损失。不同偏心距h下的气隙磁密的峰值基本不变,维持在0.95T左右。说明采用不等厚磁极可以有效改善空载气隙磁密波形,增强波形正弦性,同时会带来一定的磁密下降,设计时需要综合考量。
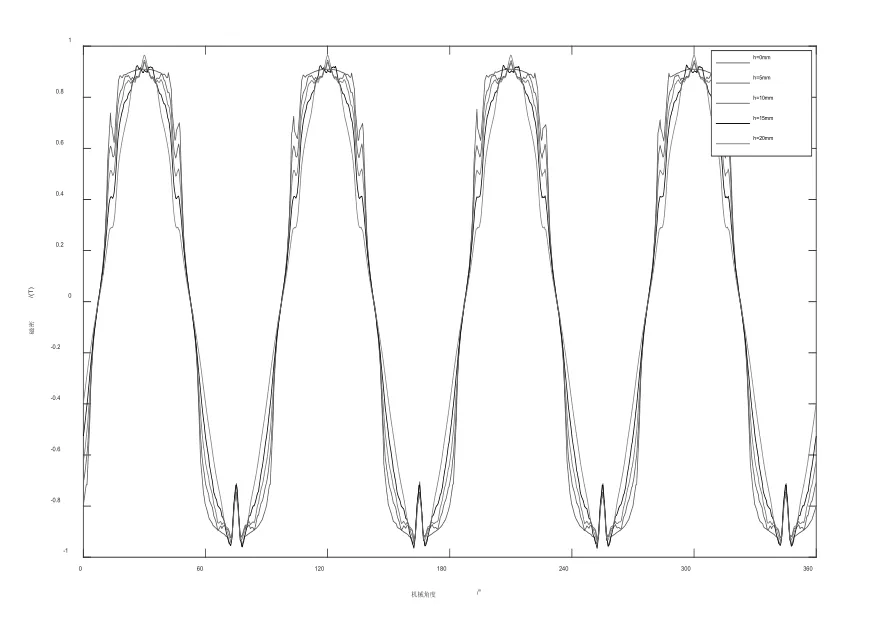
图5 不同偏心距h下的空载气隙磁密波形
在不同偏心距h下的空载反电动势有效值如图6所示。可以看出,随着偏心距h的增加,空载反电动势呈现出下降趋势,且反电动势下降趋势不断加快。偏心距h=0mm时,反电动势有效值最高为202.12V;h=20mm时,反电动势有效值最小为169.5V,下降幅度达到了16.14%。因此,在电机设计时不能盲目追求齿槽转矩的最小化,而是需要对伺服电机额定负载情况下的输出转矩进行计算,确保输出转矩符合性能要求,在此基础上确定最佳偏心距取值。
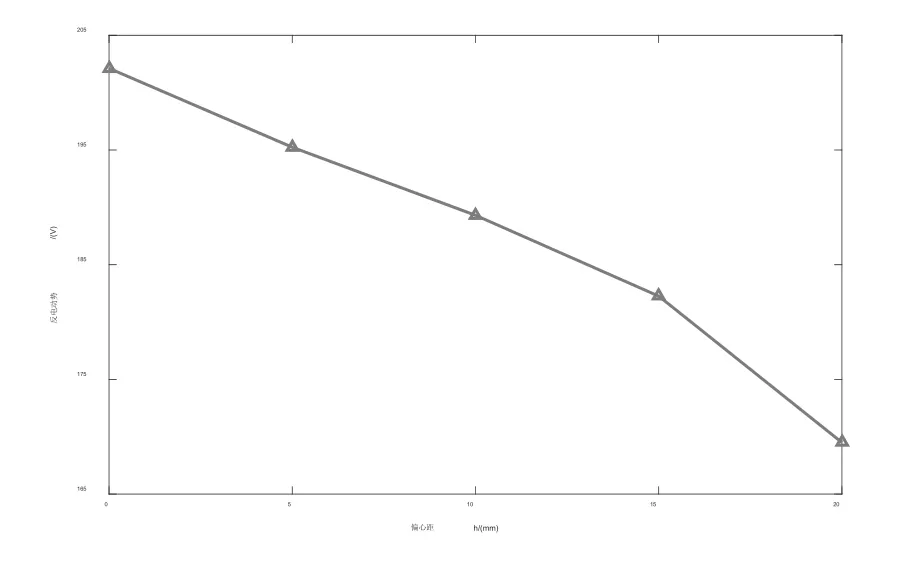
图6 反电动势有效值随h变化趋势图
3.2 额定负载计算及分析
在3000r/min的额定转速下,对伺服电机的额定负载情况进行仿真计算。得出不同偏心距h下的输出转矩波形如图7所示。图中可以看出,随着偏心距h的增加,输出转矩平均值呈下降趋势。h=0mm时,输出转矩最大为15.09Nm;h=20mm时,输出转矩最小为11.68Nm,下降了约22%。
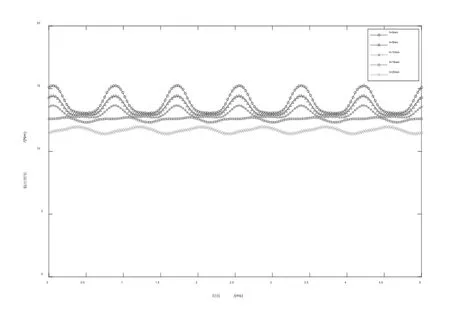
图7 不同偏心距h下输出转矩波形
将不同偏心距下输出转矩的具体参数汇总如表2所示,可以看出,当h=15mm时,输出转矩平均值为12.54Nm,输出转矩峰峰值最小为0.4Nm,转矩脉动为3.2%。此时伺服电机的输出性能满足要求,且具有最小的转矩脉动,综合对比来说偏心距取15mm伺服电机的性能最佳。
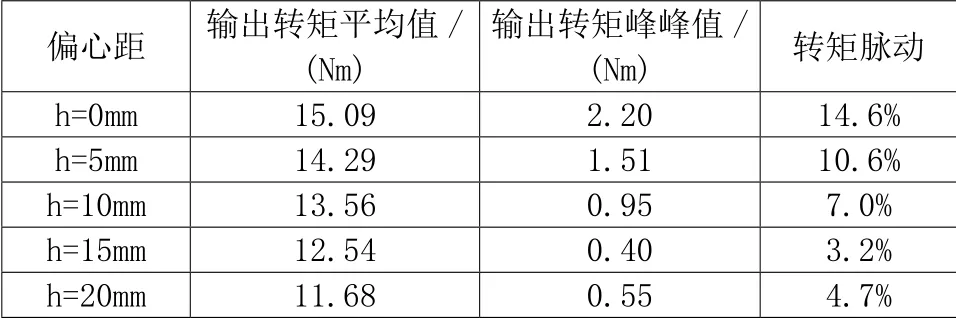
表2 不同偏心距下的输出转矩参数
值得注意的是,在空载齿槽转矩的仿真中,齿槽转矩的最小值出现在h=20mm处,但转矩脉动的最小值确并不在h=20mm这个位置。这是因为h的变化不仅会改变齿槽转矩的大小,还会影响空载反电动势的大小和波形。h=15mm与h=20mm时的反电动势波形如图8所示。可以看出,h=15mm时的空载反电动势波形正弦性比h=20mm时更好,谐波含量更低。而转矩脉动的大小除了受到齿槽转矩的影响外,还跟反电动势的谐波含量有很大关系。因此,多种因素的综合影响下,最终h=15mm时出现转矩脉动的最小值。
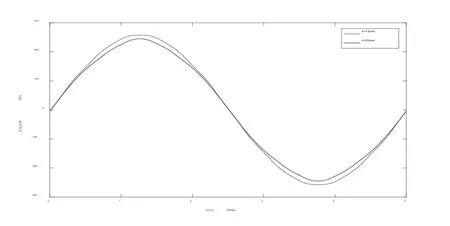
图8 不同偏心距下的反电动势波形对比
综上所述,选择伺服电机的偏心距h=15mm作为伺服电机优化后的设计方案,此时,额定情况下输出转矩平均值为12.54Nm,转矩脉动为3.2%,满足输出性能和转矩脉动的要求。
4 结语
本文利用有限元分析软件,对一台3.65kW的永磁同步交流伺服电机进行了仿真计算,对比分析了不同偏心距下电机的空载及负载性能,得到以下结论。
(1)采用不等厚磁极的方法可以大大削弱伺服电机的齿槽转矩,电机的齿槽转矩随着偏心距的增加会不断下降。
(2)增加磁极偏心距在削弱齿槽转矩的同时,也会导致电机的空载反电动势和额定情况下的输出转矩下降,在电机设计时应综合考量,避免输出性能损失过大。
(3)改变磁极偏心距还会影响到电机反电动势的波形正弦性,选取合适的偏心距可以大大降低反电动势的谐波含量。转矩脉动的大小会同时受到齿槽转矩和反电动势谐波含量的影响,齿槽转矩最小时转矩脉动并不一定会最低。
