基于相场法的周期性多孔结构断裂行为研究1)

应宇轩 黄玮, 马玉娥 彭帆

*(西北工业大学航空学院,西安 710072)

†(长安大学理学院,西安 710061)

引言

若材料在空间上由重复的且周期性的代表性单元(单胞)组成,则称之为周期性结构[1].多孔结构是一类由随机或周期性的微观结构组成的轻质结构,其材料主要包括金属、高分子以及陶瓷3 大类[2].随机多孔结构又可称为泡沫结构,周期性多孔结构常包括蜂窝结构、波纹结构等.因多孔结构独特多样的性能特点,逐渐成为了诸多领域学者研究的重点和热点.多孔结构具有隔热、轻质、吸音、相对密度低、比强度高、可变形等优异的性能,在航空航天、柔性电子器件、能量吸收、隔音和组装框架等领域有着广泛的应用[3].

断裂破坏问题的预测一直以来都是学术界和工程界关注的难题.由于内部存在相互贯通或封闭的孔洞和不同的外部加载模式,周期性多孔结构的断裂行为更加具有不确定性.Hayes等[4]探讨了单胞孔洞为正方形的周期性多孔合金在复杂加载模式下的断裂失效行为,杜映洪[5]给出了分层蜂窝周期性多孔结构在复杂应力状态下的断裂模式,Jelitto等[6]探究了泡沫多孔材料断裂韧性、裂纹扩展与孔隙率、加载方式的关系,均说明了多孔材料断裂时的裂纹扩展路径会受到孔洞影响,且随着外部加载模式的改变,裂纹扩展行为与裂纹数量也发生改变.因此可以发现,周期性多孔结构在复杂力学环境下,会呈现出复杂的力学响应与失效模式[3].经典断裂力学理论难以解决裂纹形核以及扩展方向等问题[7-8],因此迫切需要寻找合适的断裂问题数值模拟方法.

传统有限元框架下模拟裂纹扩展的数值分析方法主要有单元删除法[9]、界面单元法[10]、扩展有限元(XFEM)[11-12]等.单元删除法将满足条件的单元应力置0,但难以模拟裂纹分岔问题.界面单元法通过设置内聚力单元模拟裂纹扩展,但具有较强的网格依赖性.扩展有限元法通过扩充形函数使裂纹可以在网格内扩展,但较难处理三维问题[13].本文所采用的相场(phase-field)断裂模型是一种弥散式裂纹模型.该方法基于传统Griffith[14]理论,通过能量平衡理论研究裂纹的扩展行为.Francfort等[15]在该理论基础上提出了断裂变分准则,Bourdin等[16]通过引入弥散的相边界来表征裂纹的尖锐边界,引入序参量(即相场)来得到空间中描述损伤的标量场,并经过相场方程控制序参量的演化来显式追踪裂纹扩展路径,极大地简化了算法实现的复杂度.目前,相场断裂方法已经广泛应用于脆性断裂[17]、塑性断裂[18-19]、动态断裂[20]、疲劳裂纹扩展[21]、各向异性材料断裂[22]、多场耦合[23]等问题.该方法在三维模拟方面也体现出了优势[24].对于复合材料、周期性点阵、周期性多孔结构等可能出现的裂纹轨迹难以预测、多裂纹交汇问题,相场法具有其独特的优势[25].

基于多尺度分析方法和均匀化理论[26],周期性结构宏观模型的力学行为可以通过分析细观尺度的代表性体积单元(representative volume element,RVE)模型的力学性能来表征,细观力学分析方法如图1 所示.在多尺度分析过程中,需要满足基于均匀化理论的细-宏观能量等价条件(hill-mandel 条件)[27].此外,需要给RVE 模型施加周期性边界条件,来保证RVE 边界处的变形、应力连续,由宏观模型向微细观模型传递信息[28].

图1 细观力学分析示意图Fig.1 Mesomechanics analysis schematic

尽管多孔结构在单轴、双轴或剪切载荷下的力学响应已经被广泛研究[29-30],但在实际情况中,周期性多孔结构往往承受多轴复杂载荷,目前对于该方面断裂问题的研究较少.此外,以往的大多数周期性边界条件只是控制RVE 模型中对称边界的位移,但不能保证作用在RVE 模型上的多轴宏观应力的比值恒定不变.

本文基于ABAQUS 有限元软件平台建立了周期性多孔结构的RVE 模型,施加以多轴加载比例为控制参数的周期性边界条件,实现了对于RVE 模型的比例加载,结合相场断裂方法从而研究周期性多孔结构在复杂多轴加载状态下的断裂失效行为.

1 相场断裂方法

1.1 断裂变分准则

首先在本文中定义φ∈[0,1] 的标量来定义相场变量表示裂纹拓扑.当φ=0时表示材料完好,φ=1时表示材料完全破坏,引入一维杆件的弥散裂纹模型与相场函数[31],如图2(a)和图2(b)所示,其裂纹表面密度函数为

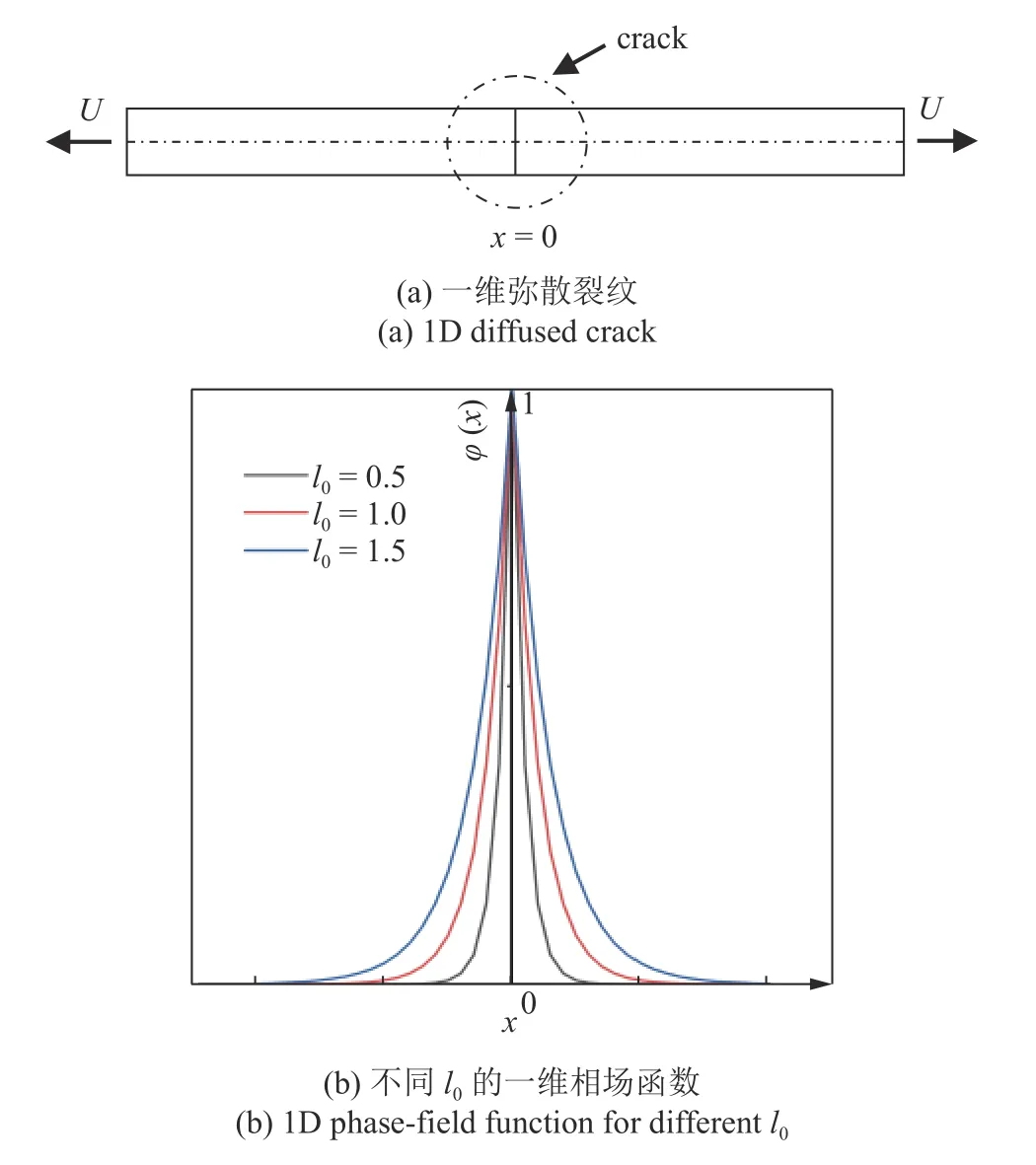
图2 一维杆件的弥散裂纹与相场函数Fig.2 Diffused crack and phase-field functions in 1D rods

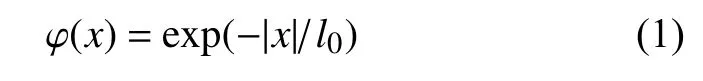
由此推导出二维和三维的表面密度函数

式中,l0代表裂纹的弥散宽度.

断裂变分原理认为弹性体 Ω 的势能 ΠΩ由弹性应变能Estr和断裂表面能Wfrac组成,其表达式为

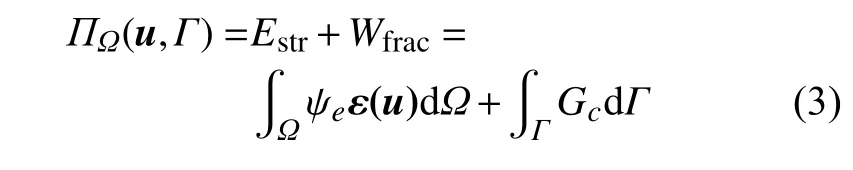
式中,ψe为弹性应变能密度,ε(u)为应变张量,Gc为临界能量释放率.

由于在损伤过程中应变能会减少,故引入二次退化函数

式中,k是一个很小的参数,可以防止φ=1 时刚度矩阵奇异.本文取k=1.0×10-7,因此有

1.2 相场控制方程

图3 弥散裂纹与弹性体受力情况,左侧为尖裂纹,右侧为弥散裂纹Fig.3 Diffused crack and elastomeric stresses,with sharp cracks on the left and diffused crack on the right

系统的总势能 Π=ΠΩ-Wext,其对φ和u求变分后可以得到

式中,n为法线向量,σ和u分别为柯西应力张量和位移张量.根据变分原理,式(7)应满足 δΠ=0,因此得到相场与位移场耦合的形式为

1.3 弹性应变能的拉压分解

考虑到材料中只有拉伸载荷会引起裂纹扩展,若不分离应变能中的拉应力和压应力部分,会产生裂纹伪分岔现象[32].首先对应变张量进行谱分解

式中,ε+为拉应变张量,ε-为压应变张量,εi为主应变值,ni为主应变值的方向.m代表空间维数,尖括号算子定义为:〈x〉+=(x+|x|)/2,〈x〉-=(x-|x|)/2.由此,弹性应变能密度分解为

式中,λ和µ为拉梅常数.考虑到刚度退化仅作用于拉伸应变能,则 ψe可表示为

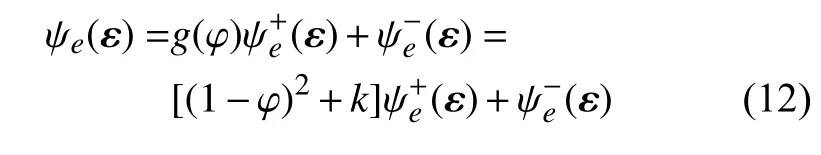
1.4 相场断裂模型的分步算法

相场控制方程组往往是非线性的,若通过Newton 迭代法直接求解,在ABAQUS 隐式求解中容易造成不收敛.因此,可以对控制方程进行解耦,使位移场方程和相场演化方程交错迭代求解.本文用一层UEL 计算相场,一层UMAT 计算位移场并完成可视化[33].

首先推导式(9)中方程的弱形式

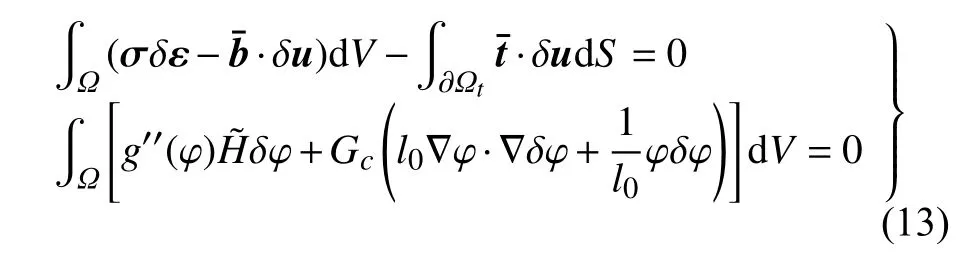
对位移场和相场变量进行离散可得

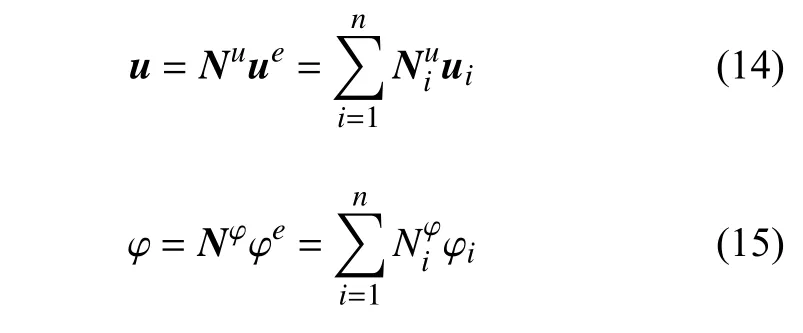
式中,n是每个单元的结点数,Nu和Nφ分别为单元的位移场矩阵和相场形状函数,和分别为结点i的位移场形状函数矩阵和相场形状函数,其表达式如下所示

式中,Ni为结点i的形状函数.相应地可以得到u和φ的梯度表达式为

式中,Ni,x和Ni,y为结点i处的形状函数分别对x和y的导数.将上述离散后的值代入弱形式平衡方程(13)中,可以分别得到位移场和相场的右端残余向量为

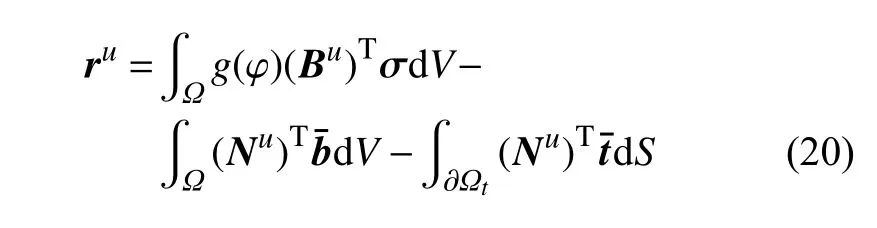
为了能够获得稳定的隐式求解公式,采用Newton-Raphson 迭代法,对位移场和相场进行解耦求解,表达式如下

式中,C0为弹性体的初始刚度矩阵.

2 多轴比例加载的周期性边界条件

在尺度转换的分析过程中,常用体积平均应变和体积平均应力来描述RVE 模型的各项宏观特性.在本文中,以作用在RVE 模型上的名义应力作为宏观量.首先,RVE 模型的宏观和细观第一Piola-Kirchhoff 应力张量表示为PM和Pm,其宏观和细观变形张量表示为FM和Fm

式中,V0和Ω为RVE 模型的体积和域.通过式(25),可以实现尺度转换下对应参量的转换,使RVE 模型的宏观名义应力可用于表征宏观模型的承载能力.

2.1 周期性边界条件

如图4 所示,在二维笛卡尔坐标系下,x1和x2分别表示水平方向和竖直方向,RVE 模型的尺寸为2l1×2l2.考虑RVE 模型处于多轴加载状态[34],P11,P22和P12分别为作用在RVE 模型上的水平、竖直方向的宏观名义应力和面内剪切名义应力.

图4 基于多轴加载的二维RVE 模型Fig.4 2D RVE model based on multiaxial loading condition

在施加双轴以及面内剪切载荷的工况下,RVE模型的宏观变形张量可以写为

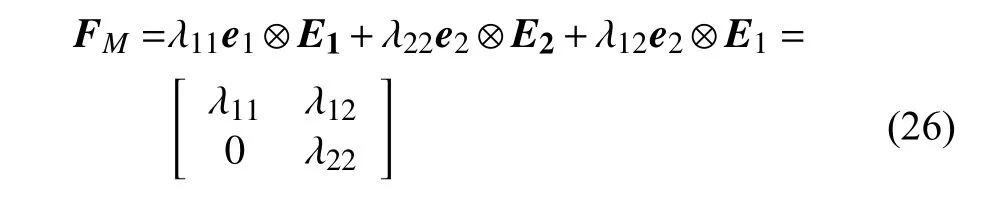
式中,λ11和λ22分别是RVE 模型水平、竖直方向的宏观变形量,λ12是面内剪切的宏观变形量.ei(i=1,2,3)是当前变形下的笛卡尔坐标系基向量,Ei(i=1,2,3)是未变形时的笛卡尔坐标系基向量.

RVE 模型的广义周期性边界条件表示为

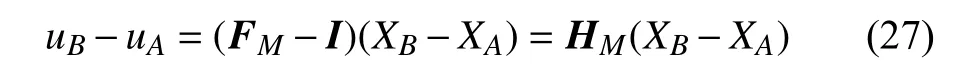
式中,uA和uB是RVE 模型中任意两对称边界上节点对的当前位移,即图4 中用红色部分标出边界A和边界B,或用蓝色标出的边界A和边界B;XA和XB是RVE 模型中对称边界上节点对的初始位置;HM是宏观应变张量,I则是单位张量.

根据Hill-Mandel 的宏、细观能量守恒条件,整个RVE 模型的宏观应变能密度应等于该模型中所有单元的平均应变能密度,其数学表达式为

静力加载下,忽略体力和惯性的作用,RVE 模型在多轴加载下的宏观总功变化率可以表示为

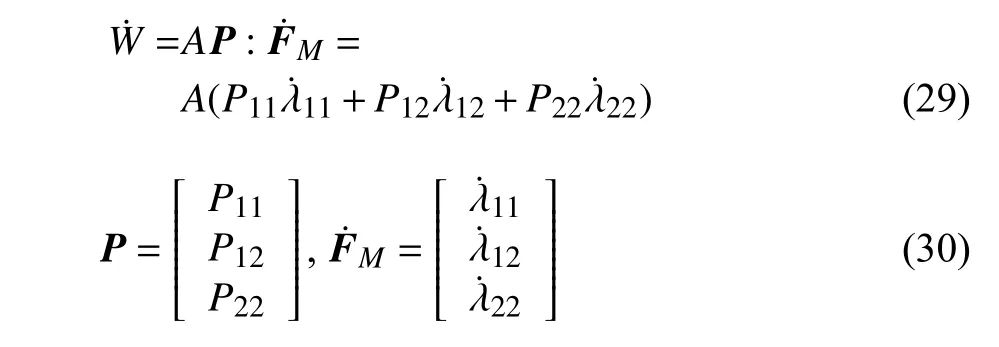
式中,A是二维RVE 模型的面积,P为RVE 模型的宏观应力张量,是宏观变形变化率梯度张量,为宏观变形率.

2.2 比例加载周期性边界条件的数值实现

引入虚拟节点,在虚拟节点上施加相应的位移载荷,可以将周期性边界条件施加到RVE 模型上.基于均匀化思想,通过能量守恒将RVE 模型的宏观应力、应变与虚拟节点的自由度、反力关联起来.

如式(26)所示,在多轴加载条件下,RVE 模型的宏观变形梯度张量FM存在3 个非零分量.在二维平面内,每个节点可以提供两个自由度,因此本文需要引入两个虚拟节点ghostnode1和ghostnode2.

首先,考虑RVE 模型在水平和竖直方向的变形能与作用在虚拟节点ghostnode1 的外力做功应满足能量相等的条件,用变化率的形式可以表示为

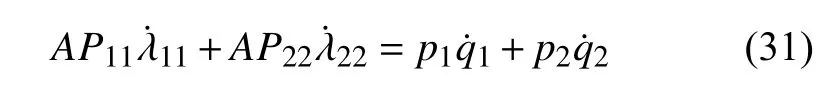
式中,q1,q2和p1,p2分别是虚拟节点ghostnode1在水平(x1)方向和竖直(x2)方向的位移与反力.上面的公式意味着变换前后的内积不变,因此两者应满足正交变换

在式(32)中,令p1=0,可以得到

从而可以得到虚拟节点ghostnode1 上的非零反力p2的表达式为

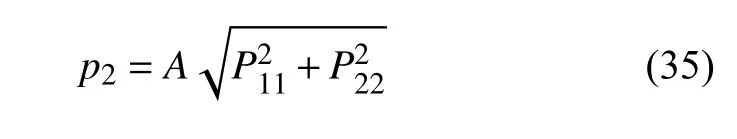
然后引入剪切应变能,考虑RVE 模型的总变形能与作用在虚拟节点ghostnode2 的外力做功应满足守恒的条件,同样用变化率的形式可以表示为

式中,q3,q4和p3,p4分别是虚拟节点ghostnode2在水平方向和竖直方向的位移与反力.同理,通过正交变换可以得到下式

1.2方法 对照组采用常规小儿肺炎对症治疗,具体措施为:帮助患儿取合适体位促进痰液快速排出体外,确保患儿呼吸通畅;对患儿采取抗感染治疗,静脉滴注30-40万U/kg/d的青霉素钠与50mg/kg/d的头孢唑啉,同时服用复合维B、维C与小儿止咳颗粒,体温超38.5℃患儿需使用药物退热。研究组在对照组基础上加用盐酸氨溴索(江苏汉晨药业有限公司,国药准字H20066523)与盐酸丙卡特罗(四川大冢制药有限公司,国药准字H20093290)治疗,用法用量:盐酸氨溴索10-30mg/次,根据年龄调整剂量,3次/d;盐酸丙卡特罗12.5-25μg/次,根据年龄调整剂量,2次/d,共治疗1周。

在式(37)中,令p3=0,则有

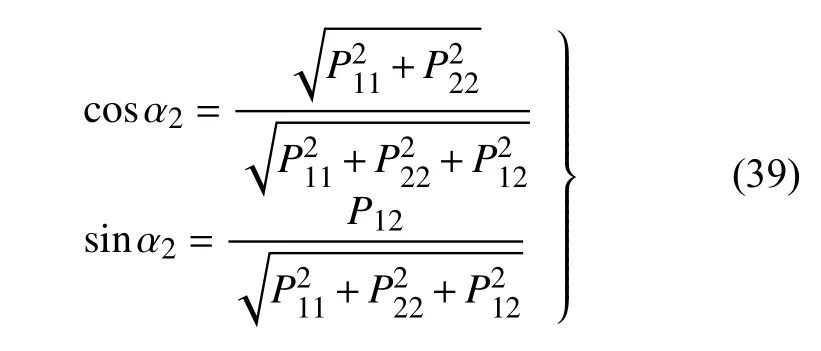
此时,作用在虚拟节点ghostnode2 的非零反力p4为

通过式(33)和式(38)的逆变换,可以得到

综合式(41)和式(42),对虚拟节点自由度重新编号,可以得到关联RVE 模型宏观变形率与虚拟节点位移变化率的转换矩阵T

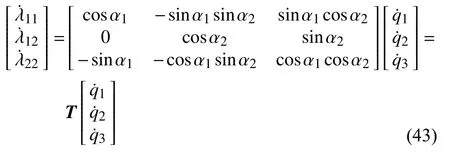
同理,可得RVE 模型宏观名义应力与虚拟节点反力的转换方程

式中,q1,q2和p1,p2分别是虚拟节点ghostnode1在水平方向和竖直方向的位移和反力,q3和p3分别是虚拟节点ghostnode2 在水平方向的位移和反力.

以RVE 模型在竖直方向的宏观名义应力P22作为参考应力,则可以用两个应力比参数来描述作用在RVE 模型上3 个宏观应力之间的关系

将式(45)代入式(34)和式(39),与 α1和α2相关的三角函数可以表示为

由式(43)可以得到RVE 模型在右边界(x1=l1)的节点位移方程为

同理,RVE 模型在上边界(x2=l2)的节点位移方程可以表达为

本文的数值仿真工作基于ABAQUS 通用有限元分析软件平台(版本:6.14)开展,比例加载的周期性边界条件通过编写ABAQUS 的用户子程序(user subroutine) 实现.在数值模拟中,只在虚拟节点ghostnode2 的水平(x1)方向施加位移载荷q3,则该方向的节点反力p3为非零值.当多轴加载的应力比参数已确定,通过式(49)即可求解得到RVE 模型在竖直(x2)方向的宏观名义应力

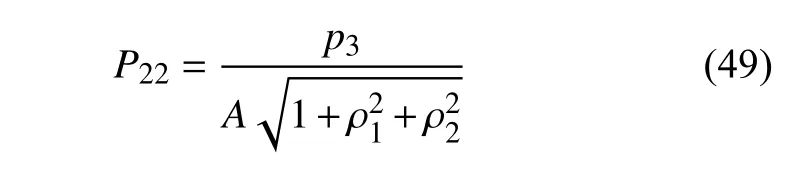
然后,通过宏观应力比关系就可得到加载过程中作用在RVE 模型上的其他宏观名义应力.

3 多轴比例加载下的周期性多孔结果断裂行为研究

3.1 周期性多孔结构的RVE 模型

针对周期性多孔结构,本文建立其二维RVE 模型,其中含孔单胞的数量为 2×2,尺寸为5 mm×5 mm,孔洞半径R为 1.0mm,RVE 模型的几何构型如图5 所示.其有限元模型采用四边形平面应变单元(CPE4)划分网格,单元数为115 200,节点数为116 637,模型中对称边界上的节点数均为241 个.

图5 周期性多孔结构RVE 模型的几何构型(单位:mm)Fig.5 Geometric configuration of the RVE model for periodic porous structures(unit:mm)

RVE 模型的裂纹弥散宽度l0=2h,其中h为模型网格的最小尺寸.对本文建立的模型,h=13 μm,l0=26 μm.

本文计算所用的材料拉梅弹性参数分别为λ=121.15 kN/mm2,µ=80.77 kN/mm2,临界能量释放率Gc=2.7 N/mm[35].计算过程中加载步长固定为Δu=5 μm.

3.2 与 8×8 常规边界条件模型的计算结果比较

为了验证采用比例加载周期性边界条件后所表征的断裂行为的正确性,本文建立了一个施加常规边界条件的 8×8 周期性多孔结构模型,模型下端约束竖直方向的位移,上端施加位移载荷.并与2×2的RVE 模型在单轴拉伸条件下断裂行为的数值模拟结果相比较.

8×8周期性多孔结构的边界条件与几何构型如图6 所示,模型下端约束竖直方向的位移,上端施加位移载荷;其孔洞半径R为 1.0mm,有限元模型的单元数为204 800,节点数为210498,l0=80μm,采用的材料参数与 2×2 RVE 模型一致.

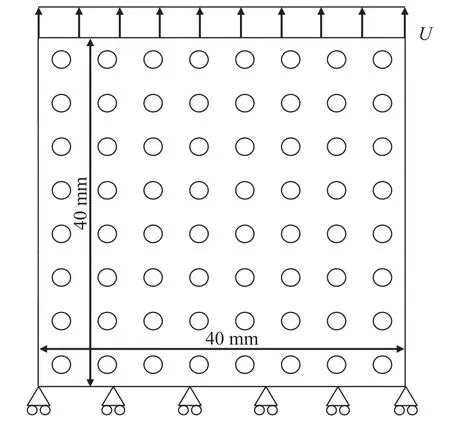
图6 8×8 多孔模型的单轴拉伸边界条件Fig.6 Boundary conditions for uniaxial stretch of 8×8 periodic porous model

对于2×2 RVE 模型,施加x2方向单轴拉伸载荷时,应力比 ρ1=ρ2=0.在加载过程中,作用在虚拟节点ghostnode2 上的非零反力p3的峰值为p3-max=86 791 N,通过式(49)可以计算得到RVE 模型在x2方向宏观名义应力的极值P22-max为867.91 MPa,这即是周期性多孔结构在单轴拉伸条件下的极限强度.

为了验证 2×2 RVE 模型网格独立性,本文在原有115 200单元数模型的基础上,分别建立了单元数为80000和156 800的稀疏网格和加密网格模型,后两者的最小单元尺寸分别为h=15.7 μm和h=11.2 μm,裂纹特征宽度参数依然取为l0=2h.3 组不同单元数的模型在单轴拉伸载荷下的名义应力-应变曲线如图7 所示.可以发现,3 组模型的曲线吻合度较高,极限载荷值相差极小.因此综合考虑模型计算精度和计算成本,本文选择单元数为115 200的 2×2 RVE模型进行后续研究与讨论.

图7 单轴拉伸载荷下单元数分别为80000,115 200和156 800的周期性多孔结构的2×2 RVE 模型名义应力-应变曲线的比较Fig.7 Comparison of nominal stress-strain curves of the RVE model with 80000,115 200and 156 800elements under tensile loading condition

此外,Miehe等[32]在应用断裂相场方法时,也对模型的网格独立性开展了相似讨论,同样发现模型网格的疏密程度对于得到的载荷-位移曲线影响程度较小.

如图8 所示,在单轴拉伸载荷作用下,基于2×2 RVE 模型与基于 8×8 常规模型得到的名义应力-应变曲线吻合较好.可以发现,两条曲线在断裂失效时刻的承载极限P22-max和应变值 ε22都几乎一致.

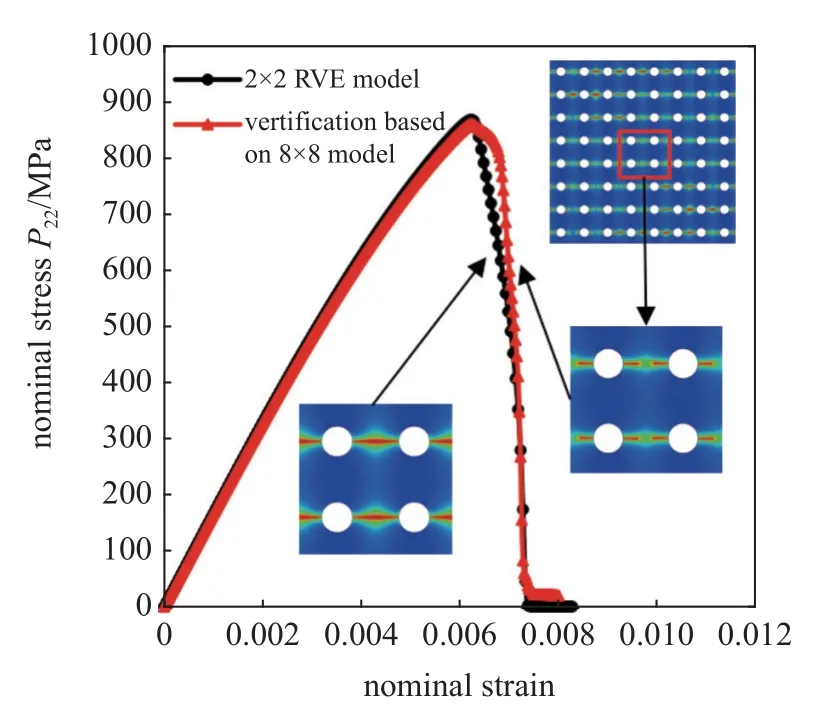
图8 单轴拉伸载荷下周期性多孔结构的 2×2 RVE 模型与 8×8 模型的名义应力-应变曲线的比较Fig.8 Comparison of nominal stress-strain curves of the 2×2 RVE model and the 8×8 periodic porous model under uniaxial tensile loading condition

图9 分别为周期性多孔结构的 2×2 RVE 模型与 8×8 常规模型在施加竖直(x2)方向单轴拉伸载荷后的渐进断裂相场云图.在相同的加载条件下,比较图9(a)和图9(d)、图9(b)和图9(e)、图9(c)和图9(f) 的断裂相场云图发现,周期性多孔结构的2×2 RVE 模型与 8×8 常规模型均是在孔边水平位置萌生裂纹,并且裂纹均沿水平方向扩展(φ=1 的路径).在相同的应变值下,两种模型的裂纹扩展模式基本一致.图9(f)中模型的破坏程度不完全一致是由于,在本文所给的常规单轴拉伸载荷作用下,受边界条件的影响,8×8 模型内部孔洞的应力分布与模型边缘孔洞的应力分布有一定的差别,模型内部孔洞的应力状态更接近RVE 模型的应力状态.8×8模型边缘孔洞的应力集中稍大,因此孔边裂纹的扩展会稍快于中间位置的孔洞.从宏观上来看,可以认为周期性多孔结构的 8×8 常规模型与 2×2 RVE 模型的裂纹扩展模式基本一致,且本文图8 中两组模型的名义应力-应变曲线吻合较好.因此,采用RVE 模型研究周期性多孔结构在复杂加载下的力学响应及断裂行为是有效可行的.

图9 单轴拉伸载荷下的周期性多孔结构的 2×2 RVE 模型与 8×8 模型的断裂相场云图Fig.9 Phase-field fracture contours of the 2×2 RVE model and 8×8 model for periodic porous structure under uniaxial tensile loading

综上所述,本文采用基于多轴比例加载的周期性边界条件的RVE 模型,可以正确有效模拟周期性结构在复杂载荷作用下的力学响应,从而评估结构的宏观力学性能.通过典型算例验证,表明该多尺度分析方法与相场断裂方法相结合用以研究周期性多孔结构在多轴加载下的损伤断裂行为具有可行性和可靠性.

3.3 双轴比例加载下周期性多孔结构的断裂行为

首先考虑周期性多孔结构在双轴载荷作用下的断裂行为,即令剪切应力比 ρ2=0.以RVE 模型在竖直方向的拉伸载荷为主应力,研究水平方向载荷的引入对多孔结构的裂纹萌生、扩展以及承载能力的影响.这里选取双轴应力比 ρ1=-1,-0.5,0,0.5,1 ;当 ρ1<0时,表明在水平方向施加的是压缩载荷.

表1 给出了当 ρ2=0时,周期性多孔结构的2×2 RVE 模型在不同双轴应力比 ρ1下的竖直方向的拉伸承载极限P22-max和断裂相场云图.可以发现,RVE 模型在承受一个方向的拉伸载荷时,另一个方向的拉伸载荷会提高结构的承载能力,而另一个方向的压缩载荷则会促进裂纹的扩展,降低结构的承载能力.

表1 双轴比例加载下的周期性多孔结构的承载极限 P22-max 与断裂相场云图Table 1 Extreme load P22-max and phase-field fracture contours for the RVE model under biaxial proportional loading condition

值得注意的是,当 ρ1<1 时,孔边裂纹扩展路径保持水平.当 ρ1=1.0时,模型表现出十字正交型裂纹扩展模式.这是由于多孔结构的RVE 模型具有中心对称性,在双轴等值拉伸载荷作用下,模型在两个方向产生等量的变形,水平和竖直方向的孔边应力、应变状态相同.因此,当双轴应力比 ρ1=1.0时,孔边裂纹在水平和竖直方向同时萌生并同步扩展.

3.4 多轴比例加载下周期性多孔结构的断裂行为

在3.3 节的基础上,引入面内剪切应力,在周期性边界条件模型中改变剪切应力比 ρ2的取值,讨论周期性多孔结构在同时承受双轴和剪切的复合加载下的断裂行为.由于在面内剪切方向上,顺时针和逆时针的剪切载荷具有对称性,为了减少计算成本,本文的P12只选取为顺时针方向,并且仍以竖直方向的拉伸载荷P22为主应力.这里,ρ2的考察范围为[0,1],取值分别为 ρ2=0.25,0.5,0.75,1.0.

表2 给出了周期性多孔结构的2×2 RVE 模型在不同多轴比例加载工况下的断裂相场云图.观察表2 后可以发现,在不同的双轴应力比 ρ1和剪切应力比 ρ2组合范围内,RVE 模型的裂纹萌生和扩展模式存在一定的规律性.为此,归纳5 种不同的裂纹扩展模式的表征符号和渐进破坏的相场演化云图,如表3 所示.

表2 多轴比例加载下的周期性多孔结构的断裂相场云图Table 2 Phase-field fracture contours of periodic porous structure model under multiaxial proportional loading

表3 5 种不同裂纹扩展模式的表征符号和渐进破坏的断裂相场云图Table 3 Representative symbols and progressive phase-field fracture contours for the five distinguished crack propagation modes

从多孔结构的断裂失效模式来看,当 ρ1<0且ρ2较小时,裂纹从孔两边对称萌生,初始扩展路径与水平轴成一定的夹角,在扩展过程中与相邻孔边裂纹相互靠近并最终汇合成为S 型单裂纹;当 ρ1>0且ρ2较大时,孔边裂纹萌生点、初始扩展方向与水平轴的夹角进一步增大并趋向于45°,裂纹扩展方向随载荷的增加逐渐转向水平,最终扩展至水平相邻孔边形成双弧线型裂纹.

Sarac等[36]对错位排列的金属玻璃异质周期性多孔结构施加单轴拉伸载荷,并认为孔洞附近同时存在拉应力和剪应力,实验结果如图10所示,水平相邻的孔洞之间呈现双弧线型的裂纹,并逐渐扩展到相邻的孔洞位置.虽材料不同,该实验结果与本文多孔结构在相似载荷工况下的模拟结果较一致,可以认为采用本文所提出方法得到的模拟结果是有效可信的.

图10 错位排列的金属玻璃异质周期性多孔结构在单轴拉伸载荷下的断裂行为[36]Fig.10 Fracture behaviour of MG heterogeneous periodic porous structures under uniaxial tensile loading[36]

对于S 型和双弧线型裂纹模式来说,随着 ρ1和ρ2的增大,裂纹萌生、扩展与水平方向的夹角均逐渐增大.当双轴应力比 ρ1=1.0时,施加面内剪切载荷后,多孔结构呈现出45°斜裂纹扩展模式,而且剪切应力的增大对45°斜裂纹的扩展路径并无显著影响.

图11 给出了在不同多轴加载比例下,周期性多孔结构在竖直方向的拉伸承载极限P22-max随应力比ρ1和ρ2变化的曲线.曲线上的不同标记点符号对应于表3 中相应的裂纹扩展模式,并以黄色“×”符号表示裂纹扩展模式的转变点.

从图11 中可以发现,当双轴应力比 ρ1固定时,随着剪切应力比 ρ2的增加,多孔结构在竖直方向的拉伸承载极限显著降低;而且,ρ1越大,承载极限下降的幅度越明显,说明本文所研究的周期性多孔结构的抗剪切性能较弱.

图11 周期性多孔结构在竖直方向的承载极限 P22-max 随应力比ρ1和ρ2 变化的曲线:(a)保持应力比 ρ2 不变,(b)保持应力比 ρ1 不变,(c)局部放大图Fig.11 Changing curves of 2-directional extreme load P22-max withρ1 and ρ2 for periodic porous structures:(a) keep ρ2 unchanged,(b) keepρ1 unchanged and(c) partial enlarged graph

当0<ρ2≤0.5 时,随着 ρ1由负向正增加,即横向载荷由压缩向拉伸状态转变,多孔结构在竖直方向的拉伸承载能力呈先增加后减少的趋势;而当0.5<ρ2≤1.0时,结构的承载极限随 ρ1的增加而降低;说明:随着剪切载荷的增加,其对多孔结构极限强度的影响逐渐起到主导作用.

此外,当 ρ1=1.0,ρ2=0,即多孔结构承受双轴等量拉伸载荷时,其极限承载强度达到最大值.

图12 总结了周期性多孔结构在复杂多轴比例加载范围内的断裂相图.根据表3 中所列出的5 种裂纹扩展模式,断裂相图总共被划分为5 个区域,并用黄色虚线表示断裂模式转变的相边界,图12(b)、图12(c)和图12(d)分别为相图局部区域的放大图.

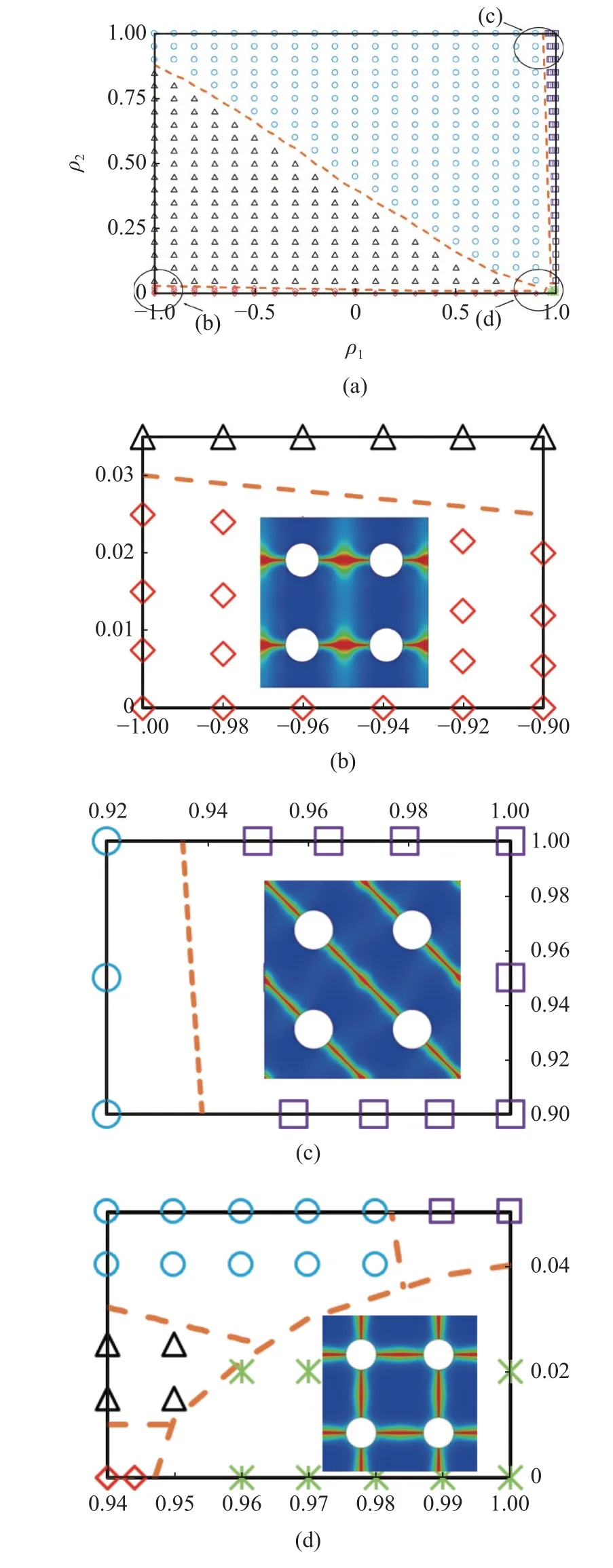
图12 周期性多孔结构在不同多轴加载条件下的裂纹扩展模式相图Fig.12 Phase diagram of crack propagation mode for periodic porous structure under different multiaxial proportional loading

在双轴和剪切载荷同时作用下,周期性多孔结构的裂纹扩展模式主要呈现为S 型与双弧线型,且这两种扩展模式的分界线(即相边界)呈近似线性.当剪切应力比 ρ2≤0.03 时,裂纹扩展模式由S 型向水平裂纹过渡;当双轴应力比 ρ1≥0.94 时,裂纹扩展模式由双弧线型向45°斜裂纹过渡;在ρ1≥0.95 且ρ2≤0.04的很小区域内,裂纹扩展模式呈现十字正交型.

观察图12 可以发现,当剪切应力比 ρ2趋近于0时,面内剪切应力P12相对于竖直方向的拉伸应力P22已经很小,可以认为RVE 模型退化为承受竖直和水平方向的双轴比例加载,多孔结构表现出水平裂纹扩展的失效模式;同理,当双轴应力比 ρ1趋近于1 时,模型承受水平和竖直方向的等量加载并耦合面内剪切加载,多孔结构展示出45°斜裂纹扩展的失效模式;当作用在模型上的多轴应力趋近于等值状态时,结构表现出十字正交裂纹扩展的失效模式.

4 结论

本文建立了周期性多孔结构的RVE 模型,采用相场断裂方法结合周期性边界条件,通过引入两个多轴应力比控制参数,实现模型在复杂应力状态下的恒定比例加载,并探究其在多轴比例加载工况下的裂纹萌生、扩展行为和承载极限等力学问题.数值仿真结果得到如下结论.

(1)采用细观力学方法,建立RVE 模型,施加比例加载的周期性边界条件,可以正确表征周期性结构的宏观力学性能.在此基础上,与相场断裂方法相结合,可以有效模拟周期性多孔结构在复杂加载条件下的断裂行为.

(2)周期性多孔结构在双轴加载状态下,剪切应力比 ρ2=0.结构在承受单轴拉伸载荷基础上,另一个方向的拉伸载荷会提高结构的拉伸承载能力,压缩载荷则会降低结构的承载能力,且双轴加载下裂纹扩展路径保持水平.当双轴应力比 ρ1=1.0时,多孔结构表征出十字正交裂纹的断裂模式,这是由结构的几何、载荷和边界条件的对称性导致的.

(3)周期性多孔结构在同时承受复杂多轴比例加载条件下,剪切应力比 ρ2>0.从承载极限来看,随着面内剪应力的增加,结构的极限拉伸强度显著降低,而且双轴应力比 ρ1越大,强度极限下降幅度越大;当0<ρ2≤0.5 时,随着 ρ1增加,多孔结构的抗拉强度先提高再降低;当0.5<ρ2≤1.0时,结构的抗拉强度随着 ρ1的增加而持续下降,但下降幅度不大.从裂纹萌生与扩展行为来看,周期性多孔结构展现出S 型、双弧线型和45°斜裂纹型3 种模式;对于前两者,ρ1和ρ2的增大时,裂纹扩展后与水平方向的夹角逐渐增大;对于后者,ρ2的增大对其裂纹扩展路径并无显著影响.