考虑相变的近场动力学热-力耦合模型及多孔介质冻结破坏模拟1)

2023-01-15李星顾鑫夏晓舟陈爱玖章青

力学学报 2022年12期

李星顾鑫夏晓舟陈爱玖章青,

*(河海大学力学与材料学院,南京 210098)

†(华北水利水电大学土木与交通学院,郑州 450045)

引言

多孔介质材料组成的结构服役于寒冷潮湿的环境时,其内部会发生传热传质和相变现象.多孔介质中孔隙水的冻结将导致材料变形,诱发材料的损伤甚至破坏失效,如寒冷地区混凝土结构的冻融破坏[1-2]和岩土体的冻胀破坏[3]均与材料内部水的冻结有关.孔隙水结冰时体积膨胀,将导致冰与孔隙壁发生相互作用,与此同时,相变潜热的释放也将影响结构的温度场和变形场,是一个复杂的热-力耦合问题.发展能够准确刻画包含材料相变过程的热-力耦合模型及其数值计算方法,模拟真实的水结冰过程和其中的热-力耦合效应,对于揭示含水材料的冻胀破坏机理具有重要的科学意义.

在进行热-力耦合问题模拟时,准确求解温度场是获得结构变形场的基础.材料的相变问题具有强非线性(不同相之间物理性质的快速变化)和不连续(不同相之间边界、裂纹)的特征,在进行固-液相变的热传导数值模拟时,需要将固-液界面的演化作为解的一部分进行确定,亦称为“Stefan”问题,相应的数值求解方法主要有界面跟踪法和固定网格法[4-6].界面跟踪法使用移动网格数值方案来捕获固-液移动边界,将整个求解域在相变界面处分为固相域和液相域分开求解,该方法需要在每一个时间步长下确定固-液两相界面的位置且在相变界面上施加“Stefan”条件,求解不易实施,不适用于复杂的相变界面.固定网格法使用固定网格方案,将求解域中固相和液相编写入一组控制方程进行求解,此类方法通过对控制方程中传输量的跃变来考虑相变过程,不需要跟踪固-液两相界面的位置,代表性方法有热焓法模型[7-8]、显热容模型[9-10]和等效热容模型[10]等.

连续介质力学理论建立了偏微分型的热-力耦合方程,但在求解含孔洞、演化裂纹等强非线性和不连续问题时面临瓶颈.近场动力学(peridynamics,PD)采用空间积分方程描述力学响应,在数值求解时不存在空间求导,可以有效避免传统连续性模型求解时出现的病态特征[11-12],为热致变形破坏等问题的数值模拟提供了新思路[13].

起初,近场动力学主要用于研究机械载荷作用下材料和结构的损伤破坏问题,随后被用于模拟各种扩散问题.Gerstle等[14]首次在近场动力学框架内建立了非局部扩散模型,研究了一维物体中的热传导过程,为扩散问题的PD 建模奠定了基础.此后,PD 理论逐步被应用到热传导领域中,研究者先后构建了键型 PD 多维非稳态热传导模型[15-16]与态型PD热传导模型[17-19],并对多维结构、多种边界条件、含缺陷和裂纹的热传导问题进行了模拟,证明了PD理论在求解热传导问题时的有效性.但上述PD 热传导模型都未涉及相变问题的描述,Madenci等[20]用近场动力学微分算子将偏微分型的热焓方程改写为积分型方程,模拟了物质的一维相变过程,模拟结果和解析解吻合较好.Nikolaev等[21-22]率先建立了包含材料相变的键型PD 热传导模型,求解了均质物质一维冻结和二维对流传热相变问题,对比解析解验证了模型的正确性,为键型PD 热传导模型中考虑相变提供了理论参考.

近年来,PD 理论也被广泛应用到热致变形及热致损伤破坏问题的研究中[23-24].国内外学者建立了多种近场动力学热-力耦合模型,通过对大量的热传导问题的分析,证明其在分析热致损伤及破坏问题时的可行性.目前建立的PD 热-力耦合模型主要包括非耦合的模型和全耦合的模型两类.前者只考虑温度对结构变形的影响而忽略结构变形对温度的影响,通过在PD 运动方程中的本构力函数或力矢量状态中引入温度影响项构建PD 热-力耦合模型[25-28]后者在热传导方程中加入结构变形加热和冷却项来反映结构变形对温度场的影响,实现了温度场和变形场的双向耦合[29-31].需要指出的是,目前已建立的PD 热-力耦合模型在进行温度场的求解时还未涉及材料相变影响,材料相变时潜热的吸收与释放会显著影响温度场分布,进而影响结构的变形.据此,本文在近场动力学框架内发展了考虑相变的键型PD热-力耦合模型及其数值求解方法,模拟了饱水多孔介质在降温条件下的冻结破坏过程,以期建立合理可靠的多孔介质冻结破坏的数值模拟方法.

图1 物质点间的相互作用Fig.1 Interaction between material points xpand in PD theory

1 考虑相变的近场动力学热-力耦合方程

1.1 键型近场动力学运动方程

材料的微弹性模量c可通过PD和经典连续介质力学中的应变能密度等效获得,具体为

式中,E为材料弹性模量,ν 是泊松比,h是平面问题中板的厚度,A是一维问题中杆件的截面面积.

定义物质点对的伸长率达到某一临界伸长率s0时,该物质点对发生断裂,物质点之间不再有力的作用,用间断函数来标记物质点对的断裂状态,则有

临界伸长率s0与材料的断裂能释放率有关,表示为

式中,GF为断裂能释放率.因此,材料的损伤可以通过材料点的断裂键数与总键数之比来确定

1.2 含相变的键型近场动力学的热传导方程

在使用固定网格方案进行相变问题模拟时,热焓法被广泛采用.热焓法的主要思想是将温度、比热容和潜热合并为热传导方程中的热焓项,在整个求解域中建立统一的能量方程.通过对热焓求解即可确定两相界面,因而不需要追踪相变界面,可用来求解复杂边界条件下的相变问题[4].具体地,引入热焓H(T,x,t),将基于傅里叶定律的热传导方程重新写成以下形式[20]

式中,H(T,x,t)是t时刻x处的热焓,K是材料热传导系数,T(x,t)是t时刻x处的温度.热焓和导热系数分别为

式中,C1和C2分别是液相和固相的比热容,K1和K2分别是液相和固相的热传导系数,L是材料相变潜热,Tmelt是材料相变温度,G(T) 是Heaviside 阶跃函数.

由式(8)求温度可得

基于此,可在近场动力学框架内建立热焓形式的热传导模型,进行相变问题的模拟.采用近场动力学方法求解热传导问题不仅考虑了非局部性,而且允许不连续演化.如图2 所示,在PD 热传导模型中,质点间的非局部相互作用是伴随热能交换产生的.一个质点与其邻域内的其他质点发生热量交换,热量交换通过两个质点之间的热键(T-bond)完成,热键的相关定义与运动方程中物质点之间键的定义相同.Nikolaev等[21]给出了键型PD 中用热焓表达的热传导方程,表示为

图2 PD 模型中热键Fig.2 T-bonds in PD model

式中,kT是近场动力学中的微热导率,其与经典力学理论中的导热系数K相关,表示为

式中,K是材料的热传导系数.

如图2 所示,在近场动力学模拟中,为体现不同相之间的材料属性差异,根据热键两端连接的物质点种类的不同,把热键分为液相热键、固相热键和液-固界面热键,计算时热键的热力学参数根据热键的种类进行赋值,并根据相变状态实时更新.

综上所述,结合式(1)和式(11)即可得到考虑相变的键型PD 热-力耦合模型,第一个方程是满足热弹性本构关系的运动方程,第二个方程是热焓形式的热传导方程.需要指出的是,在该耦合模型中只考虑温度对变形的影响而忽略了结构变形对温度的影响,属于单向耦合的形式.

2 热-力耦合模型的数值求解方法

对于耦合方程组的数值求解,一般采用单步法或交错法进行.因本文热-力耦合方程为单向耦合的形式,此外为避免单步法中采用小时间增量而造成计算量过大的问题,采用交错算法对耦合方程组进行数值求解.其中,结构变形场和温度场自然分开求解,即运动方程用于求解变形场,热传导方程用于求解温度场.

数值求解时,运动方程和热传导方程采用显式差分方案进行求解,分别为

式中,n是时间步编号,i和j是物质点编号,ΔtM和ΔtT分别是运动方程和热传导方程的时间增量步.

显式积分算法虽然简单明了,但其是条件稳定的,求解时采用的时间增量步需要满足稳定性条件.可以根据von Neumann 稳定性分析方法获得稳定性时间增量步ΔtM和ΔtT[33].采用交错算法时先进行温度场的求解,将当前的温度状态看作是一个“假定稳态”,然后进行变形场的循环计算,直至此时的变形场达到稳定状态.当ΔtT和ΔtM差异很大,甚至前者高出后者几个数量级时,采用真实的ΔtM来进行变形场的计算会导致较高的计算开销.为提高求解效率使变形场快速达到稳定状态,本文运动方程采用自适应动态松弛法(adaptive dynamic relaxation,ADR)进行求解.

在ADR 方法中,系统所有质点的运动方程通过引入虚拟惯性力和阻尼项,写成一系列常微分方程[33]

式中,D为虚拟对角密度矩阵,cM为阻尼系数,分别通过Greschgorin 定理和Rayleigh 得到.F(u,u′,x,x′,t)是由PD 相互作用力和体力构成的力密度矢量.下一时间步的位移和速度可使用中心差分的显式积分方法得到

在动态松弛法中,力矢量F是唯一的物理量,密度矩阵D、阻尼系数cM和时间步长Δt不需要是物理量.因此可以选择合适的参数在满足稳定性要求的前提下,实现快速的收敛.

图3 是热-力耦合模型数值计算流程图.在进行交错求解时,对得到的位移场是否达到稳定的判断直接影响求解效率和求解精度,是程序实施的关键.本文通过物质点在当前构型和前一个时间步构型中位移差值的均方根值Er和一个足够小量 Ω 的比较来判断当前位移场是否达到稳态.当Er<Ω 时,认为位移场达到了稳定状态,进而进行下一步温度场的求解;否则,继续进行位移场的求解,直至满足稳定性条件.

图3 热-力耦合模型数值计算程序流程图Fig.3 Flow chart of numerical program of thermomechanical coupled model

3 数值算例验证与分析

3.1 方板角冻结过程模拟

由单种相变材料组成的边长为1.5 m 的正方形板,处于液相状态,初始温度T0=1.3 K,材料相变温度Tmelt=1.0K.板的左边界和下边界施加恒定的温度边界Ti=0K,上边界和右边界保持绝热.在边界温度作用下,方板从边界处开始降温并发生从左下角向右上角的冻结.为验证前述考虑相变的PD 热传导模型的准确性,模拟了相变潜热分别为L1=0.25 J/kg和L2=1.0J/kg 时方板的冻结过程.

在近场动力学模型中,方板被均匀离散,物质点间距Δx=5 mm,近场范围取δ=3Δx.材料热力学参数为,比热容Cs=Cl=1.0J/(kg·K),密度ρs=ρl=1.0kg/m3,热传导系数Ks=Kl=1.0W/(m·K),其中下标S和l分别表示固相和液相.

图4 是模拟得到的潜热L1=0.25 J/kg 的方板在不同时刻的温度场分布和相变界面位置.从图4(a)中可以看出,模型在边界温度作用下开始降温,当材料温度低于相变温度时发生冻结,冻结过程由左下角向右上角发展.在图4(b)中,蓝色表示液相,绿色表示固相,红色表示相变的界面.从图中可以看出,方板在冻结过程相变界面自左下角开始向右上角移动,符合方板冻结的客观规律,说明PD 方法能够追踪到冻结过程中相变界面位置,可以有效模拟出方板的角冻结过程.

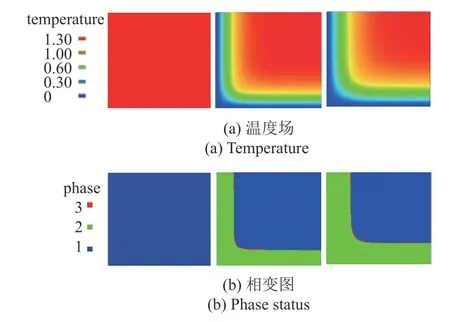
图4 方板角冻结PD 模拟结果Fig.4 PD simulation results of square plate corner freezing

图5 给出了时间为0.1 s 时相变界面位置,并列入了Kovačević等[34]采用有限体积法FVM和基函数配点法RBFCM 得到的结果.可以明显看出,在采用不同的相变潜热L1=0.25 J/kg和L2=1.0J/kg 时,PD 方法捕捉到的相变界面位置和文献[34]用两种方法模拟得到的结果均吻合较好,充分验证了本文给出的含相变的PD 热传导模型在求解含相变的热传导问题时的有效性.

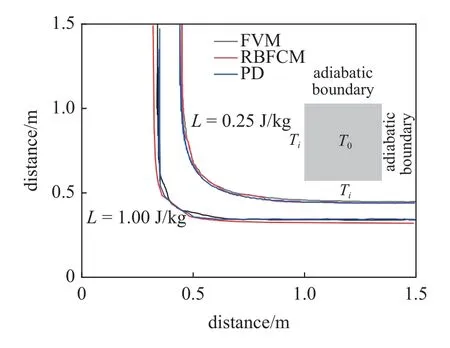
图5 相变界面位置比较Fig.5 Comparison of phase change interface position

3.2 方板热致变形模拟

如图6 所示,假设正方形板边长为1 cm,初始温度为T0=10°C,上边和右边受到降温载荷Ti=1°C的作用,左边和下边绝热并约束法向位移.将该模型作为平面应变问题,分别利用PD 热-力耦合模型和有限元软件ABAQUS 模拟了该方板在降温时的力学响应.

图6 受到双面温度载荷作用的正方形板Fig.6 Square plate subjected to double side temperature load

在近场动力学模拟中,方板被均匀离散,物质点间距Δx=0.1mm,近场范围取δ=3Δx.材料热力学参数如下[35],弹性模量E=25.7 GPa,泊松比ν=0.25,热传导系数K=1.0J/(s·m·K),密度ρ=1800kg/m3,比热容C=1688J/(kg·K),热膨胀系数α=1.8×10-5K-1.

图7 给出了近场动力学和有限元模拟得到的板在t=200s 时的温度场和位移场云图.可以看出,在相同的时间下,两种方法得到的温度场和位移场基本一致.图8 给出了两种方法模拟得到的方板中A,B,C三个位置处的温度和水平方向的位移的时间历程曲线,随着时间的增加,方板温度由右上角向左下角逐渐降低,温度降低引起材料收缩,A和B处的水平位移为负值,这与热胀冷缩的实际情况相符.模拟表明,无论是在同一温度下还是随着温度的变化,PD 模拟结果和有限元结果都吻合较好,验证了PD 热-力耦合模型在求解热力耦合问题时的准确性.

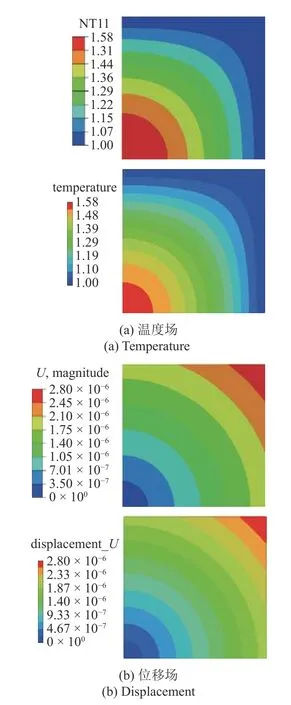
图7 有限元(上)和近场动力学(下)模拟的t=200s 时结果比较Fig.7 Simulation result comparison of finite element and periynamics at t=200s

图8 近场动力学和有限元模拟得到的A,B,C 点温度和位移时间历程比较Fig.8 Comparison of temperature and displacement histories of points A,B and C obtained from peridynamics and finite element simulation

3.3 多孔介质的低温冻结破坏模拟

基于前述建立的热力耦合模型及其数值计算方法,建立如下的计算模型来模拟多孔介质的冻结破坏过程.混凝土是典型的准脆性材料且其冻融破坏比较常见,因此选用混凝土材料进行说明.虽然导致混凝土冻融破坏的因素很多,众多学者也先后提出了多个理论模型来揭示混凝土冻融破坏的机理,但因孔隙水冻结体积增大而引起内应力从而诱发破坏已是学术界的共识.水结冰后体积增大9%,在混凝土孔隙内产生结晶压力和静水压力.由此产生的内应力超过混凝土的材料强度时,将诱发混凝土材料的损伤及微裂纹的萌生扩展,经过多次冻融循环后,最终导致混凝土结构的破坏.

如图9 所示,假设含有圆形孔隙的砂浆方板,板边长300μm,开始时孔隙内充满液态水,初始温度为T0=12°C,结冰温度Tmelt=0°C.方板上边界和右边界施加温度为Ti=-30°C 的降温条件,板左边界和下边界绝热并约束法向位移.为反映孔隙水冻结时体积膨胀效应,当孔隙冻结时在孔隙边界上施加沿着径向的位移载荷,其大小与孔隙半径相关,按照体积增大9%确定,位移载荷的施加顺序与孔隙冻结的顺序保持一致.

图9 含孔隙的砂浆方板Fig.9 Mortar square plate with pores

在近场动力学模拟中,板被均匀离散,物质点间距Δx=1 μm,近场范围取 δ=3Δx.砂浆材料参数和3.2 节的材料一致,水和冰的参数为:热传导系数Kl=0.6J/(s·m·K),Ks=2.14J/(s·m·K),比热容Cl=4182J/(kg·K),Cs=2060J/(kg·K),密度ρl=1000kg/m3,ρs=920kg/m3,相变潜热L=334 kJ/kg,其中下标l和S分别表示水和冰.

图10为模拟得到的砂浆方板冻结破坏的结果.如图10(a)所示,由于孔隙水结冰时释放潜热,孔隙和周围砂浆基质的温度变化滞后于其他区域,板内温度场的分布明显受到影响而呈非均匀分布.图10(b)为方板中孔隙水的结冰过程,其中蓝色表示砂浆基质,青色表示液态水,黄色表示冰,红色表示冰水界面.图10(c)为方板冻结过程中的损伤图.当t=0.006 s 时,靠近方板边界处的孔先开始结冰.水结冰的体积膨胀促使孔隙边界向外扩张,在较近的孔隙1和2 之间引起较高应力集中诱发砂浆基质的损伤,如图10(c)所示.随着板内温度的持续降低,更多的孔隙开始结冰.当t=0.105 s 孔隙全部冻结,板内的损伤由孔隙周边的点状分布汇聚成裂纹并在基质中扩展.从最终的损伤分布可以看出,冻结过程中裂纹的萌生与扩展主要集中分布在孔隙边界上和孔隙之间.孔隙边界上裂纹的环向扩展引起孔隙边界处基质材料剥落,是引起孔隙半径增大的主要原因,印证了在冻融实验中得出的孔隙半径随着冻融次数增加而增大的结论[1].此外,孔隙半径的增加致使孔隙内充填更多的水,会加剧冻融破坏的发生.孔隙之间的裂纹扩展导致材料内部孔隙连通性增加、渗透性提高,易在冻融循环条件下形成更多更大的宏观裂纹,是引起结构冻胀开裂、表面剥蚀和宏观力学性能下降的主要原因.