基于梯度折射率光子晶体可调谐亚波长聚焦特性的研究

黄 燕，梁斌明

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

1987年，John[1]和Yablonovitch[2]分别独立提出光子晶体这一概念。光子晶体的主要特征就是存在光子禁带[3]，即当电磁波落在光子带隙内时将不能继续传播下去。随后Luo等[4]发现二维光子晶体具有负折射效应，并且在此基础上探究得出光子晶体具有亚波长聚焦能力。除此之外，光子晶体还可以表现出一些突出特性，如成像特性[5]、成像测量[6]、可调谐光束[7]、自准直效应[8]。人们根据这些特性设计出了诸多光学元件，例如超棱镜[9]、波导[10]等。

随着对光子晶体研究的深入，人们提出了一种新型光子晶体——梯度折射率光子晶体。这一概念最早在2005年由Centeno等[11]提出。研究表明，通过适当地调整光子晶体中的参数，如填充因子的结构、晶格常数，可以得到折射率梯度渐变的光子晶体。这一发现为控制电磁波在光子晶体中的传播过程开辟了一种新途径，后续的很多光子晶体结构都受到这一理念的启发。人们对梯度折射率光子晶体进一步研究，发现了许多梯度折射率光子晶体的应用。例如，Singh等[12]通过改变梯度折射率光子晶体的结构参数，在选定的频率范围内可以控制和实现理想的光子带。Zhu等[13]发现梯度折射率光子晶体可以很好地改善由于晶体厚度增加而引起的光输出急剧下降的问题。

利用梯度折射率光子晶体实现超分辨聚焦现在已成为一个重要的研究领域。Li等[14]通过在光子晶体的中心引入一个空气孔，实现了在二维光子晶体中加入点缺陷的结构。结果表明，在透镜的亚表面和顶表面可以得到较好的聚焦光斑。但由于焦点位置的局限性，使得该结构在实际运用中比较困难。随后，Rezaei等[15]提出了一种基于液晶的梯度折射率光子晶体，通过向液晶施加外部静态电场来调节光子晶体的折射率，实现光子晶体折射率的梯度渐变。设计出的调焦系统可以实现焦距在0.255λ内的可调节。

本文继续研究梯度折射率光子晶体的亚波长聚焦。设计的光子晶体背景为硅，介质柱为圆形空气孔。通过改变光子晶体中空气孔的结构来实现折射率的梯度渐变。运用平面波展开方法分析能带图，利用二维时域有限差分（finite-different time-domain, FDTD）方法仿真光在光子晶体中的传播路径，探究影响梯度折射率光子晶体聚焦效果的因素。数值模拟分析证明，设计出的梯度折射率光子晶体可在其外部得到一个较小的聚焦光斑。同时，采用改变梯度折射率光子晶体背景温度的方法设计了一个调焦系统，该系统可实现焦距在1.5λ内的可调节。

1 梯 度 折 射 率 光 子 晶体的设计和原理

本文选用的是由圆形空气孔和硅构成的正六角形平行平板结构。光子晶体的结构如图1（a）所示，光子晶体的背景为硅（折射率为3.42），圆形介质柱为空气（折射率为1），晶格常数为a（a=482 nm），空气孔半径为r（r=0.365a）。在该结构下，选用入射波长λ=3.344a（1 612 nm）时，具有较好的实验结果。对光子晶体中的负折射效应和聚焦效果的研究，通常是从研究其光子带结构和等频表面轮廓开始的。图1（b）为通过Rsoft中的光子晶体能带结构模拟分析设计软件BandSOLVE仿真出的光子晶体第一能带的等频图。图中显示由里向外频率w的值逐渐减小，此时群速度和相速度相反，这意味着该入射波长在光子晶体中可以实现负折射现象。同时，当波长λ=3.344a时，归一化角频率w0=a/λ =0.299，由图1（b）可得，此时波矢k=3.843 8 μm-1。根据折射率公式n=kλ / ( 2π) 得出对应的光子晶体折射率n=-0.984 7。研究表明，当等效折射率接近-1时，光子晶体具有亚波长的聚焦能力。

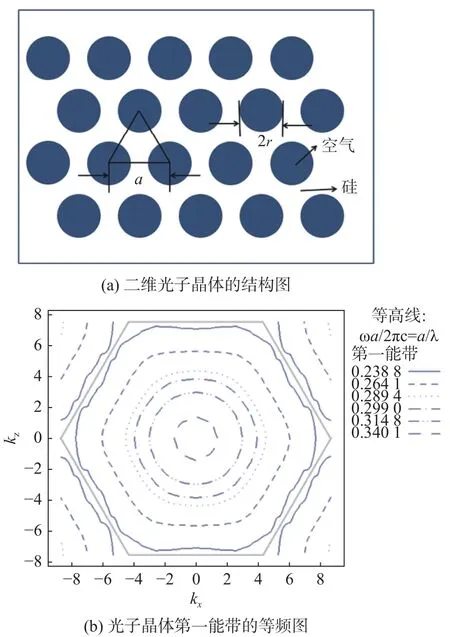
图 1 二维光子晶体结构图与光子晶体第一能带等频图Fig. 1 The structure of photonic crystals and several EFS contours in the first TE-polarized photonic band of the PC

当改变光子晶体中空气孔半径大小时，等频图中的波矢k的值也相应改变。由公式n=kλ/(2π)可知，若入射波长λ不变，则波矢k与光子晶体折射率n成正比。由此可得，光子晶体中的空气孔结构大小与光子晶体的折射率呈一一对应的关系。整体改变光子晶体中空气孔半径，令r′=mr，通过多组数据，得出m与其对应折射率n的关系为m=-0.21n2-0.85n+0.36，如图2（a）所示（其中横坐标为光子晶体折射率n，纵坐标为空气孔半径相对于r变化的倍数m）。由图可以看出，空气孔半径越大，光子晶体的等效折射率越小。

二维光子晶体可以被认为是离散介质，其中的每一列介质都是离散且均匀的。结合上述得到的空气孔半径与折射率的关系，可以通过调整光子晶体中每一列空气孔的半径，来获得折射率在横向上梯度渐变的光子晶体。根据斯涅耳定律[16]，近轴光束会逐渐向折射率高的方向弯曲。因此本文设计的梯度折射率光子晶体中心折射率最高，从内向外折射率逐渐减小。该梯度折射率光子晶体的结构如图2（b）所示。

图 2 光子晶体中空心孔半径与折射率的关系与二维梯度折射率光子晶体的结构设计图Fig. 2 The relationship between hollow pore radius and refractive index in photonic crystals and the structural design of two-dimensional graded index photonic crystal

设置每一列的空气孔半径相同，且由里向外空气孔的半径依次增加，当平行光从光子晶体的正下方入射时，经光子晶体折射后，汇聚在光子晶体外，从而实现平行光的聚焦。

2 仿真数据和结果讨论

2.1 光子晶体折射率梯度渐变的原理

如图3（a）所示，通过改变光子晶体中空气孔的尺寸（中间的空气孔尺寸最小，两边空气孔尺寸依次递增），设计了一个二维的梯度折射率光子晶体。对于一块厚度为h的光子晶体，为了实现平行光在焦距为y处的聚焦，则需要设计折射率在x轴方向渐变。假设中心一列的光子晶体的折射率为n0，距离中心距离为x处的光子晶体的折射率为nx。由于平行光实现聚焦必须满足入射面到聚焦点的光程差相同，即n0h+y=nxh+则由于在此之前讨论过光子晶体的折射率与空气孔半径的关系，因此可根据nx的值得出该列空气孔的半径。通过空气孔半径的改变从而实现光子晶体折射率的梯度渐变，且该折射率分布满足光程差的要求，在理论上可以实现完美聚焦。在Rsoft软件中利用FDTD算法，模拟仿真光在光子晶体中的聚焦过程，设置入射光源为高斯光束的平行光。图3（b）和图3（c）为根据理论折射率nx设计的光子晶体的聚焦效果和聚焦光斑的半宽图，在该图中半宽为0.705 4λ，聚焦效果较差。而且此时的聚焦属于小光瞳聚焦，对于不同孔径x，产生的负球差[17]也不同，可通过改变光程与该孔径产生的负球差相抵消，从而优化聚焦效果。在下面的设计中将对其一起进行修正。

图 3 梯度折射率光子晶体亚波长成像原理Fig. 3 Schematic diagram of sub-wavelength imaging realized by gradient index PC

2.2 光程差的修正

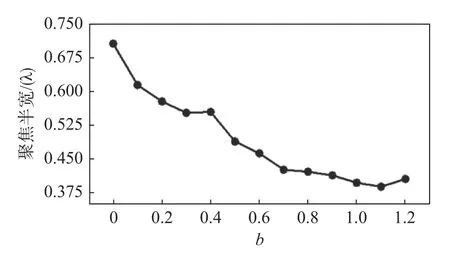
图 4 不同 的光子晶体的聚焦半宽Fig. 4 The half-width of focal spot after modifying the refractive index of the PC

2.3 焦距对聚焦效果的影响

为了获得更佳的聚焦效果，分析了焦距改变对聚焦光斑的影响。设计4种结构的光子晶体（b=0.9、b=1.0、b=1.1、b=1.2）。改 变 焦 距y（y在1.833 2～9.833 2 μm范围内变化），仿真结果见图5。可以看出，在这4种b值对应的光子晶体中，半宽值随焦距的变化趋势基本相同，当厚度为9.64 μm时，均在焦距为3.8 μm附近取得最小半宽。并且根据研究，取得最小半宽的焦距与光子晶体的厚度成正比。

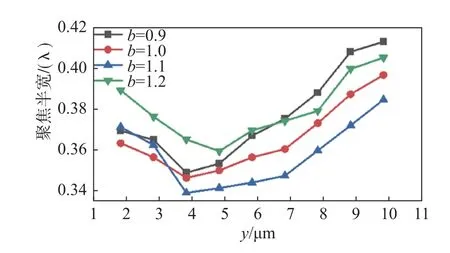
图 5 4种b值的光子晶体在不同焦距下的聚焦半宽Fig. 5 For the four structure of PCs, the relationship between the focal length and the half-width

2.4 中心空气孔半径对聚焦效果的影响

考虑到中心一列空气孔的半径也会对聚焦效果有一些影响，设计了4种结构的光子晶体（b=0.9、b=1.0、b=1.1、b=1.2），统一设置焦距y=3.833 2 μm。改变光子晶体的中心列空气孔半径r′=mr（m在0.852 1～1.040 9范围内变化）进行模拟光路。中心列空气孔半径与聚焦半宽的关系如图6（a）所示。图中4种结构的光子晶体的焦斑半宽随中心空气孔结构的变化趋势基本相同，均在m=0.95附近取得最佳半宽。综合多个因素的聚焦效果，b=0.9的光子晶体结构在m=0.954 9时取得最小半宽。综合以上数据，设计的梯度折射率光子晶体的参数如下：在光程差公 式中，h=9.64 μm，0.36），修正后的折射率此时的仿真光路传播图及聚焦半宽如图6（b）所示，对应的焦斑半宽值为0.344 7λ，焦距y=1.45λ。

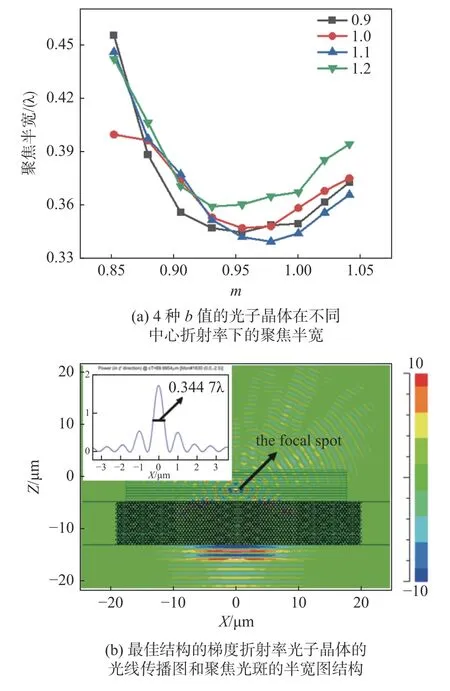
图 6 4种结构的梯度折射率光子晶体的聚焦效果Fig. 6 The results of the focal spot of the four gradient index PC structures

2.5 基于光子晶体结构设计的变焦系统

随着半宽越来越窄，焦深也越来越窄，这使得对焦比较困难。基于以上的光子晶体的结构，设计了一个变焦系统。通过温度控制，可以更好地对焦距进行调节，使得该光子晶体在实际应用中更加方便。由于光子晶体是由硅材料和空气构成，而硅材料具有热光效应[18]。在光子晶体工作温度范围（0～260 ℃）内，温度变化量与介质折射率的变化量之间的关系为：Δn= α1nΔT。其中 α1为 介 质 的 热 光 系 数, （硅 的 热 光 系 数 α1=1.86× 1 0-4/℃）, Δn为介质折射率的变化量，ΔT为温度变化量。通过半导体制冷片改变光子晶体的温度。在图3（a）中，中心一列温度为C0，边缘一列温度为C1，设置每一列的温度相同，温度由中心向边缘渐变，温度差ΔC=C1-C0。当ΔC在-120～260 ℃范围内变化时，温差与焦

距、半宽的关系如图7(a)所示。图中随着ΔC值的增大，聚焦光斑的焦距整体呈上升趋势，焦距y在1.137 4 λ～2.626 4 λ范围内变化，同时聚焦光斑的半宽都小于0.4λ。图7(b)为ΔC=-80 ℃和120 ℃的光线传播图，半宽均小于0.37λ。因此所设计的焦距可调谐梯度折射率光子晶体，在具有较大的调焦范围的同时，也具备较好的聚焦效果。

图 7 温度与焦距和半宽的关系及光路传播图Fig. 7 The focal length and half-width of PCs at different temperatures and the optical path propagation diagram

3 结 论

通过调整梯度折射率光子晶体中空气孔的结构大小，设计了一个由圆形空气孔构成的梯度折射率光子晶体结构。通过调整光子晶体中折射率的分布，优化了聚焦效果。最终得出当修正系数在0.9左右，中心空气孔半径为0.95r时，焦斑的半宽值最佳可达到0.344 7λ，焦距为1.45λ。为了便于使用，对梯度折射率光子晶体透镜的焦距调谐进行了研究，设计了一个动态亚波长的调焦系统。通过改变光子晶体的温度，获得了1.137 4 λ～2.626 4λ的焦点调谐范围，同时焦斑半宽均小于0.4λ。从而解决了随着焦点半宽越来越窄，焦深也越来越小带来的调焦困难的问题。该新型聚焦结构，适合应用在纳米光刻领域，因其较好的亚波长聚焦特性和自动调节焦距的功能，使得微器件高度集成，结构更加紧密，降低了加工成本，使得微型仪器成为可能。虽然国内目前因为实验室条件的限制，光子晶体的制备较为困难，但由于光子晶体在光通讯领域具有深远的影响，研究亚微米光子晶体仍然具有重大的意义。