基于随机游走模型的筒仓内颗粒流堵塞概率测量
2023-01-15王海涛修文正
王海涛,陈 泉,李 然,修文正,杨 晖
(1.上海理工大学 光电信息与计算机工程学院,上海 200093;2.上海理工大学 健康科学与工程学院,上海 200093)
引 言
筒仓是一种常见的颗粒物料存储设备,广泛应用于工业生产和日常生活中[1-4]。理想的筒仓能够在最小的占地面积上存储最多的产品数量,并且以所需的流量正常流出。然而,当颗粒流至筒仓出口附近时,由于筒仓壁间的距离急剧减小,颗粒之间的相互作用增强,颗粒间很容易形成较长的力链或力拱,导致筒仓颗粒流中断,形成堵塞现象。该现象不仅会产生安全隐患,更会给工农业生产带来巨大损失。因此,预测筒仓内颗粒流的堵塞概率,探究其变化规律,一直受到人们的广泛关注[5-10]。
近年来,大量研究人员通过不同的实验方法研究了筒仓内颗粒流的堵塞概率[11-17]。Goldberg等[11]通过离散元法模拟了正多边形和圆形颗粒在筒仓中的运动,发现正多边形颗粒上顶点的数目越少,堵塞概率越大,并且堵塞概率与颗粒的顶点数目呈非线性关系。López-Rodríguez等[12]采用相机对不锈钢球体在筒仓开口上方形成的堵塞拱进行拍摄,通过测量崩塌规模(〈s〉),观察到随着漏斗壁倾斜角度的增大,堵塞概率在逐渐减小。尤其,当漏斗壁倾斜角度从0°增加到80°时,堵塞的概率会减小3个数量级。Gella等[13]采用面阵CCD相机拍摄筒仓内不锈钢球体两次连续堵塞中的流动过程,发现筒仓宽度增大到颗粒直径的15~20倍过程中,筒仓中的堵塞概率在不断增大,继续增大筒仓的宽度后,堵塞概率将不再发生变化。To等[14]首次提出了随机游走模型,并成功应用于二维无摩擦漏斗系统中堵塞概率的预测。该模型根据堵塞拱的特征参数,计算出堵塞概率的预测值,将预测结果与实验结果进行比较,发现两者基本一致。在To等的研究中,该模型要求的条件过于严格,只能应用在近似无摩擦的二维漏斗中。对于有摩擦的矩形二维筒仓系统,文中并没有对该模型的适用范围作出说明[18]。
本文在上述研究内容的基础上,针对矩形筒仓,将图像法应用于堵塞拱的特征参数检测,同时结合随机游走模型计算出理论堵塞概率,重点探究在不同流量下理论堵塞概率和实验堵塞概率之间的关系。
1 实 验
1.1 实验装置
图1为实验装置示意图。本实验装置系统主要由矩形筒仓、亚克力挡板、相机和LED光源组成。矩形筒仓由有机玻璃制作而成,筒仓壁厚10 mm,高550 mm,左右壁间距150 mm,前后壁间距8 mm,筒仓孔口是位于筒仓底部的一个矩形槽,其长度8 mm,宽度R可调节,R∈[0, 8 mm]。将相机(GE1050型号,分辨率为1 024×1 024)与筒仓放置在同一水平面上,通过对筒仓孔口附近50 mm×50 mm的正方形区域进行拍照,获得颗粒堵塞后的正视图[19]。LED光源型号为SL-200W,输出功率为250 W,其光照正对孔口处,让反光点尽量显示在正视图中颗粒圆形轮廓的中心处。另外,在实验过程中,通过在筒仓内插入不同宽度的亚克力挡板,从而调整矩形筒仓的宽度(12 mm、20 mm、28 mm、32 mm、38 mm、54 mm、86 mm、120 mm)。图1中插图显示的是填充颗粒黑色电镀玻璃珠,表1为实验颗粒的特征参数。其中摩擦系数0.58是通过计算锥形颗粒堆休止角的正切值得到的,其代表的是颗粒与颗粒之间的摩擦力和作用在其表面上的垂直力之比值。实验过程中采用分布式填充方式进行颗粒加载[20],填充高度为550 mm[21]。
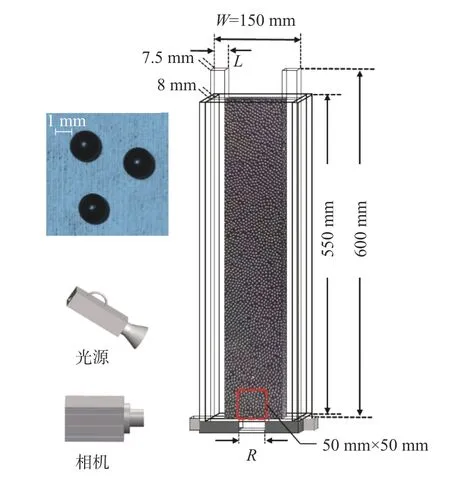
图 1 筒仓内颗粒流堵塞概率的实验装置示意图Fig. 1 Schematic diagram of the experimental system used for calculating the jamming probability of granular flow in a silo

表 1 颗粒的特征参数Tab. 1 Properties of the granular materials used in this study
1.2 堵塞拱的特征提取
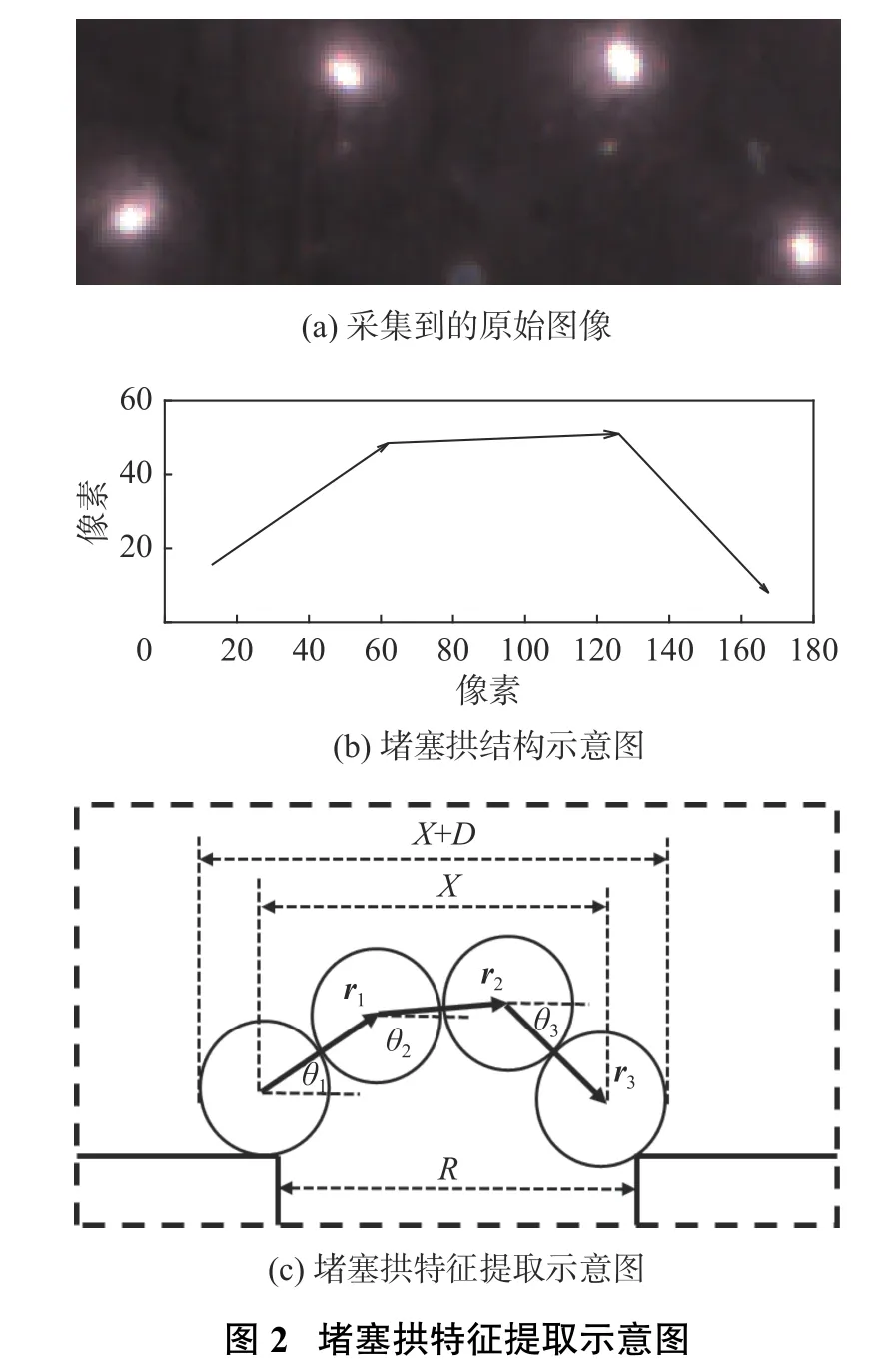
Fig. 2 Schematic diagram of feature extraction of jamming arch
图2是颗粒堵塞拱的处理过程。当筒仓内的颗粒流堵塞后,采用面阵CCD相机拍摄形成颗粒堵塞拱的正视图,将相机拍摄得到的图像裁剪成适当尺寸,使组成堵塞拱的颗粒都包含在图像中,如图2(a)所示。对于原始彩色图像,首先将图像转换成灰度图像,在灰度化处理过程中采用的是加权平均法,对彩色图像中R、G、B分量进行加权平均。其次,对灰度图像进行滤波处理,在滤波处理过程中采用的是双边滤波的方法,先用双边滤波器对灰度图像进行滤波得到低频部分,再用灰度图和低频部分作差后得到高频分量,最后将高频分量和低频分量分别增强后再进行合成,得到滤波后的灰度图像。该方法的特点是保边去噪,相较于其他滤波,在平滑图像的同时,增强了对图像边缘的保护。最后,对滤波后的图像进行全局阈值分割,通过使用最大类间方差法找到输入图像合适的阈值,再根据这个阈值将灰度图像转换成二值化图像。为了画出堵塞拱的结构图,必须求出二值化图像中每一个反光区域的中心像素坐标[22-23]。
首先,以图像左下角的像素点作为坐标原点,以水平方向为横轴、竖直方向为纵轴,相邻两个像素点间的距离为一个刻度,建立二维平面坐标系,如图2(b)所示。分别将每个反光区域中所有像素点横轴和纵轴方向最小值加上最大值的一半作为中心点坐标值( c enterX[i] , c enterY[i] ):
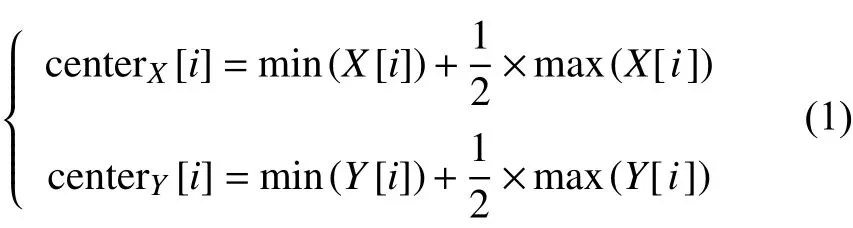
式中:X[i] 是从左向右数第i个反光区域中存放所有像素点横坐标的数组;Y[i] 是从左向右数第i个反光区域中存放所有像素点纵坐标的数组。将颗粒堵塞拱从左向右依次排序,用箭头表示有向线段并依次连接反光区域的中心像素坐标,得到图2(b)所示堵塞拱结构示意图。由于已知每个中心点的像素坐标值,再通过斜率公式和反切函数计算得到每一个有向线段与水平正方向夹角 θi:

式中: c enterY[i+1] 是第i+1个反光区域中心点纵轴坐标; c enterY[i] 是第i个反光区域中心点纵轴坐标; c enterX[i+1] 是第i+1个反光区域中心点横轴坐标; c enterX[i] 是第i个反光区域中心点横轴坐标。用ri表示第i个反光区域中心到第i+1个反光区域中心的方向向量, θi是堵塞拱上第i个颗粒的ri与水平正方向的夹角,X是堵塞拱上第一个颗粒到最后一个颗粒的方向向量的水平分量,D是颗粒直径,R是筒仓孔口宽度。如图2(c)所示,ri的长度始终等于D, θi∈[-180°,180°],X + D总是大于孔口尺寸R[24-25]。
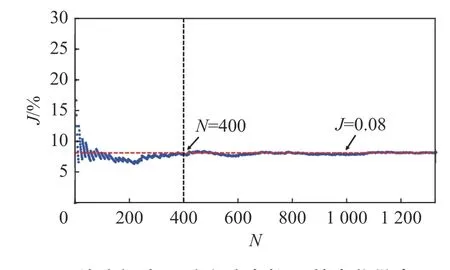
图 3 堵塞概率J随实验次数N的变化散点图Fig. 3 Scatter diagram of jamming probability J and number of experiments N
1.3 堵塞概率计算
筒仓内颗粒流形成稳定堵塞拱的过程中,离散颗粒组成的堵塞拱结构轨迹是满足随机游走模型的。该模型最早由卡尔-皮尔逊于1905年在《自然》杂志中提出[26],2001年To将该模型应用到二维漏斗的堵塞中[14]。根据堵塞拱的几何特征参数,堵塞拱的概率分布函数(an(x))可以表示为
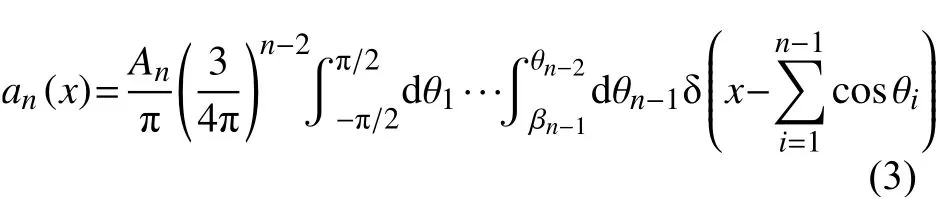
式中:n为堵塞拱上的颗粒个数;x=X/D;βn-1=max{-π/2,θn-2-2π/3} ;An是归一化系数;δ (X) 为狄拉克函数。对式(3)进一步处理可以将an(x)简化成如下公式:
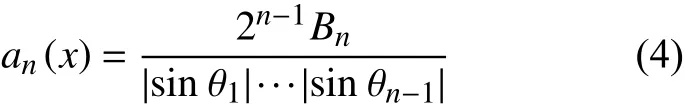
当筒仓孔口宽度为R时,对式(4)进行积分运算获得堵塞拱上颗粒个数为n时的概率(jn(R) ),其计算公式为
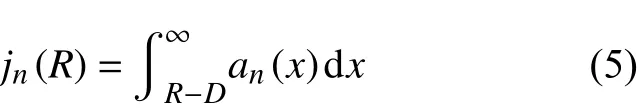
式中D为颗粒直径。因此,卸料过程中,筒仓内颗粒流发生堵塞事件的概率为
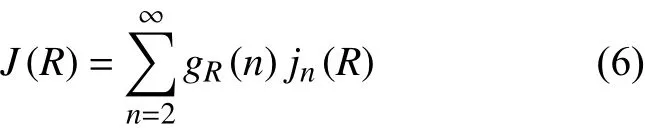
式中gR(n) 是由n个颗粒组成的堵塞拱发生的次数占总堵塞事件次数的比值。式(6)的结果就是理论堵塞概率J1的计算结果。
2 结果与讨论
本实验中,改变筒仓宽度后,加载满整个筒仓的颗粒总数量发生了改变。为了保证不同筒仓宽度条件下实验结果的可对比性,必须选择流出相同质量的颗粒作为一次实验。同时,也要满足在相同条件下,不同实验次数中筒仓孔口处流出的流量保持不变。因此,选择筒仓宽度为最小值(W=12 mm)时,在颗粒从满载流到距筒仓底部为两倍筒仓宽度位置处时,记录流出的颗粒质量为80 g±2 g。因此,在所有的实验中,以流出80 g颗粒质量作为一次实验。筒仓内颗粒的应力重定向到侧壁而引起筒仓底部压力迅速饱和,从而导致颗粒从孔口流出的流量几乎不变,这种现象必须满足筒仓内颗粒的高度是筒仓宽度的两倍以上[27]。
2.1 堵塞概率的统计

图3为堵塞概率J与实验次数N的变化散点图。在本实验中,使用图1所示装置,平底筒仓宽度为38 mm,孔口宽度为7 mm,实验的总次数N=1 325次,颗粒流发生堵塞的实验次数Na=106次。根据以下公式计算出实验堵塞概率J2=8%。从图中可以看出,当实验次数较少时,堵塞概率的变化幅值较大。这是由于筒仓内颗粒流的堵塞事件是随机发生的。当实验次数大于400次时,堵塞概率J的值趋于稳定。因此,在接下来的不同实验中,堵塞实验的总次数都设定为400次。
2.2 堵塞拱的特征值
图4(a)为2.1节中106次堵塞事件的堵塞拱上颗粒个数n的统计分布图。可以看出,堵塞拱上颗粒个数n分布在[4,16]范围内。当11<n<16时,Na随n的增大而减小。而当n>16时,Na=0。另一方面,对具有相同颗粒个数n的堵塞拱上 θi的值进行算数平均计算,得到 µθi与颗粒位置i的分布,如图4(b)所示。在误差小于5%的条件下,采用最小二乘法对测量数据进行拟合处理,拟合曲线如图中虚线所示。可以看出,当n∈[4,11] 范围内时, µθi与i呈负线性关系。这说明了堵塞拱的形状为凸形结构。而当n∈[12,16] 范围内时, µθi与i不再满足线性关系,如图4(c)所示。
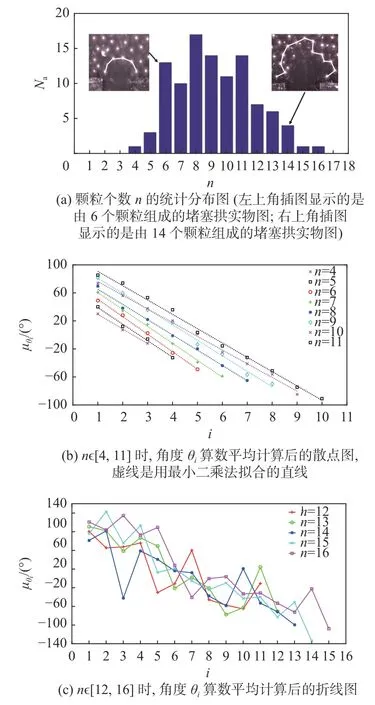
图 4 堵塞拱的特征图Fig. 4 Characteristic diagram of the jamming arch
进一步,将堵塞拱的特征参数n与 θi代入式(3)~(6)中,分别计算n∈[4,11] 、n∈[12,16] 和n∈[4,16]的理论堵塞概率J1,结果如表2所示,表2中还列出了通过实验统计得到的实验堵塞概率J2。可以看出,当n∈[4,11] 时,理论堵塞概率J1=7.7%接近于实验堵塞概率8%。而当n∈[12,16] 和n∈[4,16] 时,理论堵塞概率J1远大于实验堵塞概率J2。因此,结合图4(b)和图4(c)可以认为,在有摩擦力的筒仓中,相同筒仓宽度和相同孔口宽度下,选择堵塞拱的特征参数µθi与i呈线性关系,即选择堵塞拱为凸性拱时计算得到的理论堵塞概率要比选择非凸性拱计算得到的理论堵塞概率更接近实验堵塞概率。
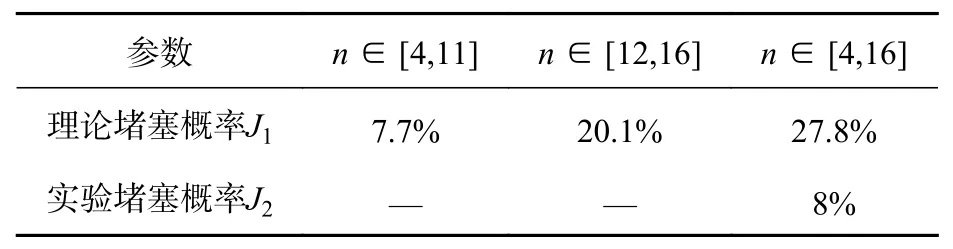
表 2 筒仓内颗粒流的堵塞概率Tab. 2 Jamming probability of granular flow in silo
2.3 流量对堵塞概率的影响
由2.2节结果可知,在相同筒仓宽度和相同孔口宽度条件下,选择凸性拱计算得到的理论堵塞概率更接近实验堵塞概率。本节中,将探究通过改变筒仓宽度和孔口宽度,选择凸性拱后计算得到的理论堵塞概率与实验堵塞概率是如何变化的。同时,再进一步讨论筒仓宽度和孔口宽度发生改变后,颗粒流出孔口的流量与堵塞概率之间的关系。
图5(a)为流量与堵塞概率随筒仓孔口宽度的变化散点图。可以看出,流量Q与孔口宽度R呈正相关关系,这与Beverloo方程所描述的流量变化趋势是一致的[28-29]。然而,堵塞概率J随R的增大而减小,即堵塞概率J与流量Q呈负相关关系,Gella在研究筒仓的堵塞与颗粒材料的运动学关系时也得出过相似的结论[13]。另一方面,在流量较小时,理论堵塞概率与实验堵塞概率存在较大偏差;而当流量Q>8.3 g/s(孔口宽度R>7 mm)时,理论堵塞概率与实验堵塞概率的差值δ<0.3%。此时,随机游走模型计算得到的理论堵塞概率能够准确预测出实验堵塞概率。
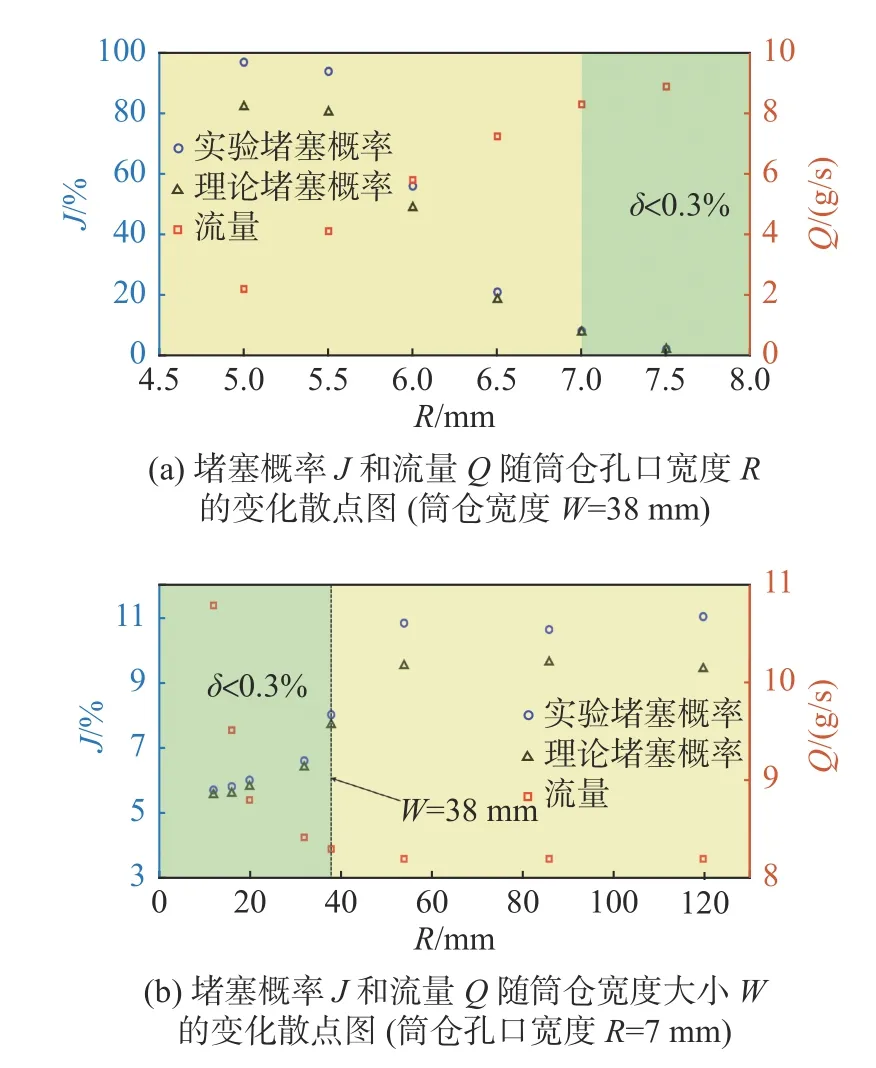
图 5 流量与堵塞概率的散点图Fig. 5 Scatter plot of mass discharge rate and jamming probability
图5(b)为流量和堵塞概率随筒仓宽度的变化散点图。可以看出,当12 mm<W<38 mm时,流量Q随筒仓宽度W的减小而迅速增大,最大流量为11.2 g/s;而当W>54 mm时,流量基本保持不变,Q= 8.3 g/s±0.1 g/s,这与Hirshfeld的研究结论相一致[30]。进一步,通过改变筒仓宽度增大流量,堵塞概率J与流量Q仍然满足负相关关系。值得注意的是,当流量Q>8.3 g/s(筒仓宽度W<38 mm)时,理论堵塞概率与实验堵塞概率之间的差值δ<0. 3%。此时,随机游走模型计算得到的理论堵塞概率能够准确预测出实验堵塞概率。
3 结 论
本文在颗粒间存在摩擦的实验装置内,通过改变筒仓孔口宽度和筒仓宽度,选用均值粒径为1.85 mm的球形玻璃颗粒,利用图像法测量了堵塞拱结构特征参数,根据随机游走模型,计算出了颗粒的理论堵塞概率,并分析了筒仓中堵塞概率的变化情况,得到如下结论:在有摩擦力的筒仓中,筒仓宽度和孔口宽度不变,堵塞拱的特征参数 µθi与i呈线性关系时,堵塞拱结构为凸性结构;无论是改变筒仓宽度还是孔口宽度,当颗粒流过筒仓孔口的流量达到8.3 g/s以上,且使用凸性拱的特征参数计算随机游走模型时,理论堵塞概率可以更加准确地预测出筒仓的实际堵塞概率。
