基于随机森林的债券违约预测

尹涛YIN Tao；李秋敏LI Qiu-min

（成都信息工程大学，成都 610100）

0 引言

债券违约指发行债券的企业在约定期限内不能向债券的持有者还本付息的情况。2014年第一起债券违约事件发生以来，我国债券违约事件日渐增多。2018年债券市场发生违约的债券有160只，涉及违约的企业有44家，违约金额更是高达1505.25亿元。截止到2021年2月，发生违约的债券总数达737只，违约债券的发行总额高达6826.37亿元。债券违约的直接后果就是投资人的利益将会受损。因此，在债券违约事件逐渐常态化的情况下，如何对发债企业的违约风险进行评估与预测，成为当下面临的重要问题。

1 文献回顾与梳理

目前，国内学者对债券违约的研究分为理论方面和模型方面。理论方面，李阳蓝（2017）以东北特钢为例，认为影响债券违约的因素有以下几个方面：融资渠道与短贷长投、偿债能力以及营运能力。刘轶军（2018）从行业发展、公司经营、财务等方面归纳影响债券违约的因素。苗霞（2018）从文献的视角归纳影响债券违约的因素，分别是宏观经济特征、行业特征、企业特征以及制度环境。

模型方面，杨世伟和李锦成（2015）基于KMV、PMF以及probit模型研究了公司债、企业债、私募债的违约概率。姚红宇与施展（2018）利用时间风险模型来研究公司特征、地方环境指标和财务指标三个因素对债券违约的影响。程昊等（2020）分析了债券违约的内外部因素，然后基于分析结果，使用Logistic模型建立了违约预测模型。

随着机器学习技术的发展，将机器学习算法应用到债券违约预测方面也成为了许多学者研究的方向。胡蝶（2018）运用债券违约归因后的一系列特征，构建了基于随机森林算法的债券违约预测模型。周荣喜等（2019）通过随机森林算法进行特征选择，然后运用选择的特征以及XGBoost算法构建了债券违约预测模型。张辰雨等（2021）运用财务指标数据，构建了基于支持向量机的债券违约模型。Zhang and Chen（2021）基于SMOTE算法和XGBoost算法构建了债券违约预测模型。

通过梳理文献，发现财务特征是影响债券违约的一个重要特征，并且机器学习算法在债券违约方面也取得了一定的研究成果。因此，本文将基于以往研究，以AIWIN平台的发债企业的财务数据为以及债券违约数据为研究对象，研究机器学习算法在债券违约预测方面的应用。首先，基于财务数据和违约数据进行标签构造以及缺失值处理，然后使用方差选择法和互信息法筛选出有效的特征，接着划分训练集和测试集，并采用SMOTE算法和Tomek Links算法结合的方法对训练集进行平衡处理，最后构建基于随机森林的债券违约预测模型，并将其与逻辑回归、决策树构建的债券违约预测模型进行性能上的对比。

2 基本算法介绍

2.1 随机森林算法

随机森林算法属于Bagging算法的扩展之一，它是以决策树模型为基学习器，通过构建多棵决策树的组合模型。为了构建多样化的决策树，随机森林算法在模型训练过程中，引入随机属性。随机分为两重随机：第一重随机是数据采样的随机，第二重随机是特征的随机抽取，即每棵决策树随机抽取部分特征来进行训练。对于回归问题采用平均法来决定最终结果，对于分类问题则采用投票法来决定最终结果。

2.2 SMOTE算法

SMOTE算法的基本思路是通过合成少数类的样本，从而使两类样本在数量上达到平衡。算法的具体流程如下：

①以欧式距离为标准，计算少数类中的每一个样本x到所有的少数类样本的距离，得到其k个近邻样本。

②对于每一个少数样本x，从其k近邻中选择若干个样本，假设近邻为xm。

③对于每一个xm，与原样本按照如下公式构造新的样本。

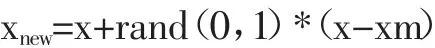
式中，rand（0，1）表示取（0，1）之间的一个随机数。合成样本的示意图如图1所示。

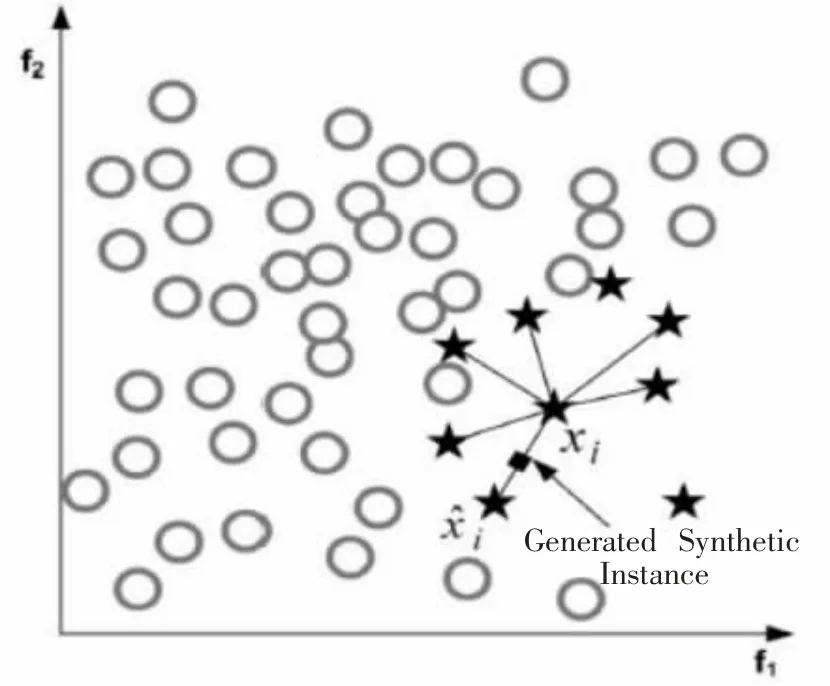
图1 SMOTE算法的原理图

2.3 Tomek Links算法

Tomek Links算法的基本思路如下：两个样本假设为x和y，分别来自不同的类别，如果不存在一个样本z，使得样本x和样本z的欧氏距离或者样本y和样本z的欧氏距离小于样本x和样本y的欧氏距离，则两个样本x和y被称为Tomek Links。如图2所示。这种情况下，两个样本被认为是噪声数据或者在边界附近。该算法通过剔除Tomek Links从而实现欠采样的目的。

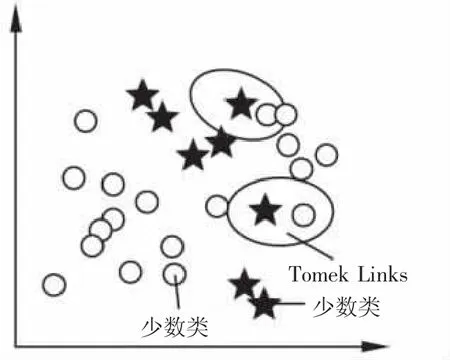
图2 Tomek Links

3 模型构建

3.1 数据来源

本文以AIWIN平台的数据作为研究对象，选取了部分企业的2018-2019年的财务数据集以及2019-2020年的违约记录数据集。财务数据集的指标主要有企业id，企业发布财务报表的日期以及企业的财务指标，违约记录数据集的指标是企业id以及发生债券违约的日期。

3.2 数据预处理

通过观察数据发现某些企业在一年里发生多次违约，这部分企业只保留一次违约记录，然后将处理后的违约数据集的企业全部标记为1，表示发生了债券违约行为。在企业违约前，财务信息往往会提前表现出一些状况，因此将2018、2019年的财务指标数据集分别和2019、2020年的违约记录数据集作拼接处理，处理后未标记的企业则标记为0，表示没有发生违约行为。

将数据集进行拼接处理后，发现大量特征存在缺失值，缺失率高达百分之二十多。常见的处理缺失值的方法有以下几种：一是直接删除含有缺失值的样本，二是用均值、中值，或者其他最常用的数值来填补缺失值。由于缺失率过高，采用填补缺失值的方法会引入大量噪声，因此本文直接删除所有具有缺失值的行。

经过以上处理后，样本的分布情况大致如下。其中发生违约的记录大约有115条，没有违约的记录大概有13000条。很明显这是一个极度不平衡的样本，需要做平衡处理。

3.3 特征选择

由于原始特征个数明显较多，有162个，因此需要进行特征选择，目的是筛选出与债券违约状况最相关的变量，便于后续的模型输入。

本文先使用方差选择法来筛选方差比较小的特征，然后使用互信息法来选择22个与债券违约状况最相关的变量。

方差选择法是通过特征本身的方差来进行特征筛选。比如，某个特征的方差很小，说明各个样本再去该特征上的值几乎没有差异，可能大多数样本的取值都一样甚至完全相同，那么该特征对于样本区分来说，几乎没有任何作用。

互信息是用来度量两个随机变量共享的信息，即在随机变量X已知的情况下，对于未知的随机变量Y的不确定性减少的程度，不确定性是用熵来衡量的。互信息的公式如下：

在特征选择中，互信息衡量了特征与标签之间相互依赖的程度，互信息值越大，依赖程度越高，特征与标签之间的相关性也就越强。筛选后的特征如表1所示。

表1 变量名称及描述

3.4 划分训练集和测试集

由于原始数据只有一份，因此有必要将数据集划分为训练集和测试集。如果将数据全部用于训练模型，得到的模型将没有任何实际意义。训练模型的最终目的是用于预测新的样本，只有当训练的模型在新样本上也有极高的精确度，即预测效果很好时，训练的模型才能应用于实际业务。本 文 采 用sklearn库 中model_selection下 的train_test_split方法，将70%的样本用于训练模型，30%的样本用于测试模型的预测效果。

3.5 样本平衡处理

不平衡的样本会严重影响模型的精确度。比如说，在研究债券违约的问题时，假设不违约的企业数量与违约的企业数量比例达到了99:1，在这种情况下，即使把所有企业都当成不违约的企业，正确率也有99%，这样就会使得模型评价变得毫无意义，无法达到建模目的——识别出违约的企业。

因此，做样本平衡是有必要的。样本平衡处理的常用方法有过采样和欠采样。过采样方法是通过增加少数类样本，从而使两类样本在数量上达到平衡，但是简单的复制少数类样本，容易使模型过拟合，模型泛化能力减弱。欠采样方法是通过减少多数类样本，从而使两类样本在数量上达到平衡，但是下采样方法会使大部分样本流失，在此条件下建立的模型很容易欠拟合，同样会使模型的泛化能力减弱。

基于此，本文采用SMOTE算法结合Tomek Links算法的方法来对训练集进行平衡处理。首先通过SMOTE算法合成新的少数类训练样本，由于在合成新的少数类训练样本时，容易出现少数类训练样本“入侵”多数类训练样本的情况，造成模型的过拟合，因此还要采用Tomek Links算法剔除噪声数据，解决少数类训练样本“入侵”多数类训练样本的问题。

3.6 评价指标

评价指标选取AUC、准确率这两个指标。AUC的值等于ROC曲线下的面积，ROC曲线是以FPR为横轴，TPR为纵轴的曲线。其中，FPR指假正例率，即真实样本为负例，预测结果为正例的样本所占的比例；TPR指真正例率，即真实样本为正例，预测结果为正例的样本所占的比例。准确率表示当样本预测为正类时，真实结果为正类的样本所占的比例。

3.7 结果分析

本文使用随机森林算法预测违约状态，然后使用AUC和准确率两个值来评价其预测性能，并对比了逻辑回归、决策树算法在该数据集上的预测性能，结果如表2所示。从准确率来看模型的预测效果，随机森林的预测效果最好，准确率为98.32%，决策树的预测效果稍次，准确率为96.95%，逻辑回归的预测效果最差，准确率仅有73.28%；从AUC来看模型的预测效果，随机森林的预测效果最好，AUC为89.96%，逻辑回归和决策树的预测效果相差不大，AUC分别为71.72%和70.41%。综合对比两个指标，可以得出结论随机森林的预测效果优于逻辑回归和决策树的预测效果。

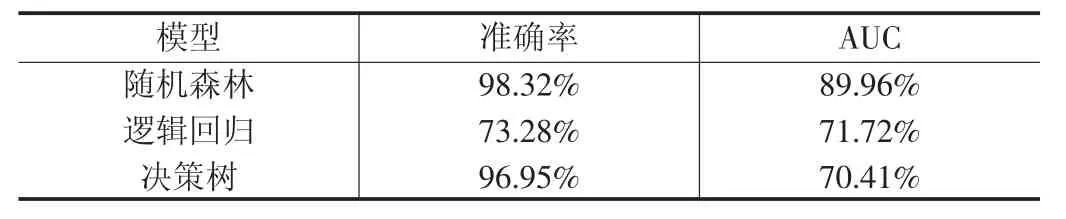
表2 评价结果对比

4 结论

本文基于财务数据构建了随机森林分类模型，对发债企业是否会发生债券违约进行了预测，并将其与逻辑回归、决策树构建的模型做了一个预测性能上的对比。考虑到样本极度不平衡以及初始特征比较多的情况，使用了方差选择法与互信息法筛选出了与债券违约最相关的部分特征，并且通过SMOTE和Tomek Links结合的方法对样本做了平衡处理。结果显示，在模型评价方面，基于随机森林构建的模型相比于逻辑回归、决策树构建的模型，AUC、准确率这两个指标的值都更高，表明随机森林算法在债券违约预测上的效果是比较良好的，对于债券违约预测的相关研究具有一定的参考价值。

本文构建的模型仍存在一些不足。正如前面文献梳理中提到的，宏观经济特征、行业特征、企业特征以及制度环境这几类特征都能作为影响债券违约影响的因素，而本文仅仅依靠财务特征来构建债券违约预测模型，存在一定的不足。如何将这几类特征纳入模型指标，可以成为未来研究的一个重点。