求解非线性互补问题的松弛模系矩阵分裂算法

谢水连

(嘉应学院 数学学院,广东 梅州 514015)

本文考虑非线性互补问题(nonlinear complementarity problem, NCP)：寻找u∈Rn使得

u≥0,v=F(u)≥0,uTv=0,

(1)

其中:函数F(u)的形式为F(u)=Au+Φ(u)+q，这里A=(aij)∈Rn×n是一个大规模的稀疏矩阵，q是一个n维向量,Φ:Rn→Rn是一个对角可微映射，即Φ的第i个分量Φi仅是u的第i个分量ui的函数:

Φi=Φi(ui),i=1,2,…,n.

显然, 若Φ是线性函数,则问题(1)就退化为线性互补问题 (linear complementarity problem, LCP).

问题(1)被称为带非线性源项的非线性互补问题.该问题在金融、交通运输等领域中有广泛应用，见文献[1-2]. 此问题引起了众多学者的广泛关注并得到了深入研究. 已有许多关于求解该问题的算法，如区域分解算法[3-4]、罚函数法[5-7]及半光滑Newton法[8]等. 值得注意的是现有的大多数算法都需要求解线性互补子问题.

1 算法及其收敛性

(Ω+M)x=Nx+(Ω-A)|x|-

(2)

令R∈Rn×n是一个松弛矩阵. 由恒等式Rx-Rx=0知, 方程(2) 等价于

(Ω+M)x=Nx+(Ω-A)|x|+R(x-x)-

(3)

即

(Ω+M-R)x=(N-R)x+(Ω-A)|x|-

(4)

基于方程(4),我们给出下列求解非线性互补问题(1)的松弛模系矩阵分裂迭代算法.

算法1令A=M-N是矩阵A的一个分裂，Ω是一个正对角矩阵，R是一个松弛矩阵,h是一个正常数. 给定初始向量x0∈Rn, 对k=0,1,2,…,求解线性系统

(Ω+M-R)xk+1=(N-R)xk+(Ω-A)|xk|-

(5)

得到xk+1,并令

显然，当R=0时，算法1就退化为文献[13]中的算法2.1. 从后面的数值实验可以看出，适当选择矩阵R可以使模系矩阵分裂算法能够更快地收敛到问题的解. 算法1给出了求解非线性互补问题的松弛模系矩阵分裂的一般框架，通过选择不同的矩阵分裂可以得到一些具体的分裂算法. 例如，令

其中D,-L,-U分别是矩阵A的对角、严格下三角和严格上三角部分. 此时，算法1称为松弛模系AOR法. 特别地，分别取α=β,α=β=1及α=1,β=0,相应的算法分别称为松弛模系SOR方法、松弛模系Gauss-Seidel方法及松弛模系Jacobi方法.

现在给出算法1收敛的2个充分条件.

当δ(R)<1时，对任何初始向量x0∈Rn, 由算法1产生的序列{xk}收敛到方程(2)的解x*.

证明设x*是方程(2)的解，由方程(4)及Ω+M-R非奇异, 可得

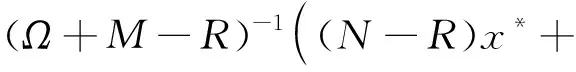
(6)

由方程(5)得

因此，

显然，若δ(R)<1， 则算法1收敛. 证毕.

Δ(R)=(I-|(Ω+M)-1R|)-1×

(|(Ω+M)-1N|+|(Ω+M)-1(Ω-A)|+

当ρ(Δ(R))<1时，对任何初始向量x0∈Rn, 由算法1产生的序列{xk}收敛到方程(2)的解x*.

证明设x*满足方程(3). 将方程(5)改写为

(Ω+M)xk+1=Nxk+(Ω-A)|xk|+

于是

(Ω+M)(xk+1-x*)=

N(xk-x*)+(Ω-A)(|xk|-|x*|)+

R((xk+1-x*)-(xk-x*))-

因为Ω+M非奇异, 所以

(Ω-A)(|xk|-|x*| )+

|(Ω+M)-1N||xk-x*| +

|(Ω+M)-1(Ω-A)||xk-x*| +

|(Ω+M)-1R||xk+1-x*| +

|(Ω+M)-1R||xk-x*| +

进一步地，可得

|xk+1-x*| ≤Δ(R)|xk-x*| ,

其中

Δ(R)=(I-|(Ω+M)-1R|)-1×

(|(Ω+M)-1N|+|(Ω+M)-1(Ω-A)|+

因此，当ρ(Δ(R))<1时算法1收敛.

2 数值实验

本节测试所提出算法的有效性. 程序用 MATLAB编写并在一台3.4 GHz CPU，8.00G RAM电脑上实现. 我们测试两个问题并与文献[13]中的算法进行比较.

算法2[13]令A=M-N是矩阵A的一个分裂，Ω是一个正对角矩阵，h是一个正常数. 给定初始向量x0∈Rn, 对k=0,1,2,…,求解方程

(Ω+M)xk+1=(N)xk+(Ω-A)|xk|-

得到xk+1,并令

在实验中，我们选择与文献[13]相同的Ω和h, 即Ω=I,h=1. 算法1中的R取为-I.

问题1考虑系统(1), 令F(u)=Au+Φ(u)+q, 其中

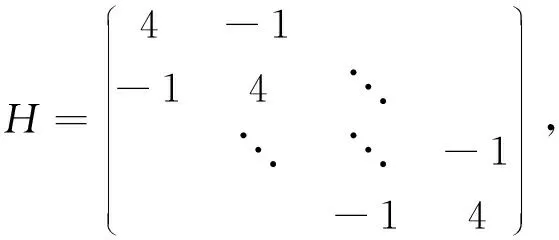
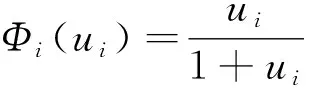
问题2考虑系统 (1), 令F(u)=Au+Φ(u)+q, 其中

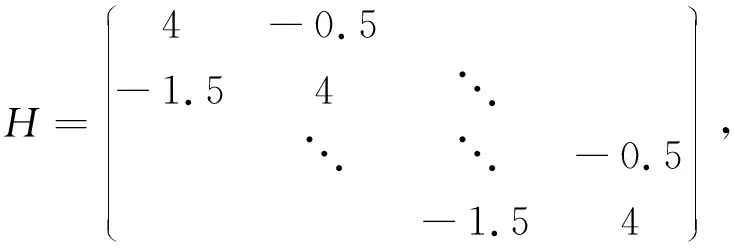
A是一个n×n矩阵,H和I是t×t矩阵，n=t2,Φ(u)=(Φi(ui))是一个对角映射,Φi(ui)=arctan(ui)且q=(-1,1,-1,1,…)T.

我们考虑两种分裂：

(ⅰ) 取M=A,N=0,此时分别记算法2和算法1为MI和NMI;

表2 采用算法1求解问题1的数值结果

表3 采用算法2求解问题2的数值结果

表4 采用算法1求解问题2的数值结果

3 结语

本文通过引入松弛变量，提出求解一类非线性互补问题的模系矩阵分裂算法. 在适当的条件下，建立了算法的收敛性理论. 与已有算法相比，所提出的算法在数值效果上有了极大改进. 接下来还有许多问题值得进一步研究，如可以考虑将此算法推广到其他类型的非线性互补问题、隐互补问题、带M函数的非线性互补问题等.另外，可以结合多重分裂算法设计求解非线性互补问题的松弛模系多重分裂算法.