轴心受压复杂卷边等肢角钢屈曲承载力试验与设计方法研究

姚行友， 张世乐 ， 程娇龙， 郭彦利， 陈梦瑶， 熊 棋， 刘亚菲， 胡成立

(1.南昌工程学院 土木与建筑工程学院，江西 南昌 330099； 2.南昌工程学院 瑶湖学院，江西 南昌 330099)

冷弯薄壁型钢构件由于刚度大、自重轻、强度高、加工和施工方便而大量地应用于轻钢房屋的建设中.近年来，随着冷弯薄壁型钢结构的推广，冷弯薄壁复杂卷边等肢角钢作为其中一类重要构件被广泛应用于塔架结构、桁架结构以及冷弯薄壁型钢建筑中.复杂卷边等肢角钢虽然截面简单，但形心和剪心不一致、板件宽厚比大、存在部分加劲板件，受力比较复杂，易于发生局部屈曲、畸变屈曲以及整体的弯曲屈曲和弯扭屈曲，目前规范计算方法不能较好地计算此类构件的稳定承载力.

Al-Sayed 等[1]进行的固接轴压等肢和不等肢角钢屈曲试验表明非弹性范围弯扭屈曲是偏于保守的.Popovic等[2]、Young[3]对冷弯平板角钢柱进行了轴压试验研究，基于试验和规范计算建议忽略弯扭屈曲的承载力计算，但只考虑弯曲屈曲承载力.Chodraui等[4]通过有限条法对轴心受压冷弯角钢柱进行分析，结果表明板件局部屈曲与整体扭转屈曲是一致的.Landesmann等[5]、Silvestre等[6]和Dinis等[7]通过轴心受压短和中长等肢角钢柱屈曲试验和有限元分析，提出了新的基于直接强度法的短到中长等肢角钢柱设计方法.Zhan等[8]采用试验和数值模拟研究了S690高强度角钢柱的弯扭屈曲性能和承载力，结果表明所有设计规范均给出了过于保守和分散的弯扭屈曲承载力，而基于直接强度法的设计方法则合理考虑了弯扭屈曲的长度依赖性以及弯扭屈曲与弱轴弯曲屈曲的相关作用.Zhan 等[9]和Wan 等[10]对S690和S960高强度等肢角钢短柱进行了试验和数值研究，结果表明澳洲和北美规范出现偏于保守和不安全的情况.Dini等[11]基于试验结果给出了短到中等长度简支热轧等肢角钢柱基于直接强度法的承载力设计方法.近年来，部分学者也对等肢卷边角钢屈曲性能和设计方法进行了尝试性的研究.Young[12]对轴心受压卷边角钢柱开展了试验，试件发生了局部、弯曲和弯扭屈曲以及屈曲模式间的相关屈曲，承载力计算表明北美规范和澳洲规范偏于保守.Young和Ellobody[13]对轴心受压卷边角钢屈曲性能进行的有限元分析表明,澳洲和北美规范对于宽厚比较大构件的承载力计算较为保守，而对于宽厚比较小构件的承载力计算偏于不安全.Shifferaw等[14]对固接冷弯薄壁卷边角钢柱整体屈曲性能进行了理论研究和有限元分析，结果表明构件发生整体弯扭屈曲时表现出显著的屈曲后强度，为此提出了考虑整体屈曲后强度的冷弯薄壁卷边角钢柱直接强度法.近年来，国内学者也对复杂卷边角钢屈曲性能进行了探索性的研究.周宜松等[15]对12根复杂卷边不等肢角钢截面冷弯薄壁型钢柱进行了轴压试验研究，结果表明北美规范中直接强度法不够精确，给出了对直接强度法中轴压构件承载力计算公式的修改意见.

鉴于目前针对冷弯薄壁复杂卷边等肢角钢柱屈曲性能与设计方法的研究较少，本文对16根冷弯薄壁复杂卷边等肢角钢轴压试件的屈曲性能和极限承载力进行实验研究，并借助有限元软件构建冷弯薄壁复杂卷边等肢角钢轴压构件分析模型.基于直接强度法和有效宽度法实验结果比较分析，提出轴心受压冷弯薄壁复杂卷边等肢角钢构件的承载力计算方法.

1 试验概况

1.1 试件设计

轴心受压冷弯薄壁复杂卷边等肢角钢由LQ550镀锌板冷弯而成.复杂卷边等肢角钢截面形式和几何参数见图1，名义尺寸见表1，其中a1、a2分别为两分肢宽度，b1、b2分别为一次卷边宽度，c1、c2分别为二次卷边宽度，t为板厚.试件包括400 mm、900 mm、1 500 mm和2 100 mm 4种长度.试件编号规则见图2， CLL6020-400-1表示两肢宽度为60 mm、一次卷边宽度为20 mm、长度为400 mm的试件，1表示相同试件的序号.试验前测得所有试件的实际长度与实际截面尺寸见表2，其中试件截面尺寸均取截面外轮廓尺寸.

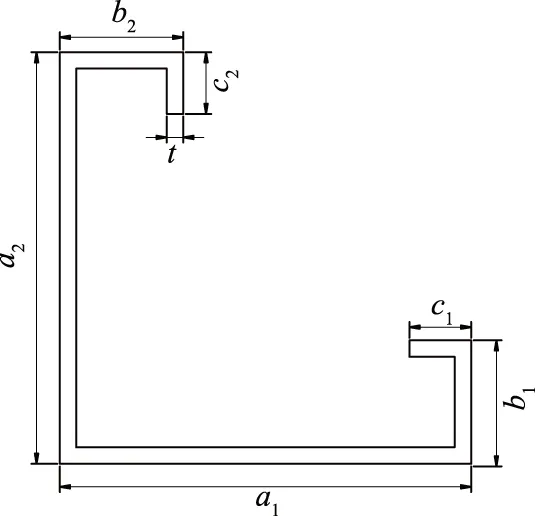
图1 复杂卷边等肢角钢截面形式和几何参数

图2 试件编号

表1 试件名义尺寸

表2 试件实测尺寸

续表

1.2 材性试验

采用与试件同批次钢板制作3个标准试件按照《金属材料 拉伸试验 第1部分：室温试验方法》(GB/T 228.1—2010)[16]采用电子万能试验机进行拉伸试验，其中一个材性试件应力-应变曲线见图3，材性试验所得钢材的材料性能指标屈服强度、抗拉强度及弹性模量的平均值为403 MPa、523 MPa和2.11×105MPa.

图3 σ-ε曲线

1.3 初始缺陷

冷弯薄壁复杂卷边等肢角钢在加工、运输、安装等过程中，会不可避免地产生初始几何缺陷.初始几何缺陷会对冷弯薄壁型钢构件的屈曲模式和承载力造成影响.为此在试验之前采用千分表对所有试件初始几何缺陷进行测量，测量位置见图4，其中在位置1、2、3处分别测量试件弱轴整体屈曲初始缺陷、畸变屈曲初始缺陷及局部屈曲初始缺陷.试件初始缺陷测量过程见图5,其中畸变屈曲初始缺陷测量在两个分肢上沿试件长度方向对长度为400 mm、900 mm和1 500 mm的试件平均取10个截面，长度为2 100 mm的试件平均取14个截面，整体初始缺陷测量在两分肢交线上所取的截面同畸变屈曲，局部屈曲初始缺陷测量在两个分肢上沿长度方向取3个截面且测点位置间隔为10 mm.

图4 试件初始缺陷测量截面位置

图5 试件初始缺陷测量

部分试件的初始缺陷测量值见图6.由图6可知大部分试件畸变初始缺陷的最大值大于局部缺陷和整体缺陷的最大值，其他试件初始几何缺陷分布规律与此类似，且最大值均小于L/1 000.

图6 试件初始缺陷

1.4 加载装置和测点布置

冷弯薄壁复杂卷边等肢角钢轴压试验加载装置见图7，采用自反力加载架和千斤顶加载，试件直接放置在上部与作动器连接的端板和下部承压端板的凹槽内，试件的几何中心与上部加载板和下部承压板几何中心重合.试件中截面位移计布置见图8，D1、D2、D3和D4距最近肢尖和肢背10 mm，分别测量试件两肢肢尖和肢背侧移.试件加载端布置一个位移计测量试件竖向位移.采用YG16静态应变位移采集系统自动采集试件承载力和侧移.

图7 试验装置

图8 中截面位移计布置

2 试验结果及分析

2.1 试验过程和试验现象

所有复杂卷边等肢角钢柱试件的屈曲破坏模式见表3，其中L、B、G分别代表局部屈曲、畸变屈曲和整体屈曲，Pt为试验的极限承载力，Pm为有限元分析极限承载力.由表3可知，对于宽厚比较小、长细比较小的试件发生畸变屈曲，而宽厚比较小、长细比较大的试件发生畸变和整体弯曲的相关屈曲；对于宽厚比较大、长细比较小的试件发生局部和畸变相关屈曲，而宽厚比较大、长细比较大的试件发生局部、畸变和整体弯曲相关屈曲.

2.1.1长度为400 mm的角钢短柱 长度为400 mm的角钢短柱屈曲破坏过程见图9，在加载初期变形不太明显，随着荷载的增大，宽厚比较大的CLL9020系列分肢出现了局部屈曲(图9a)；继续加载，试件发生畸变屈曲(图9b)，两分肢夹角变大；最终达到极限承载力时试件破坏.

图9 长度为400 mm的角钢短柱屈曲模式

2.1.2长度为900 mm、1 500 mm和2 100 mm的角钢中、长柱 角钢中、长柱的屈曲破坏过程见图10～图12.加载初期变形不明显，随着荷载增大，宽厚比较大的CLL9020系列试件分肢出现局部屈曲(图10a、图11a、图12a)；继续加载，试件出现了畸变屈曲(图10b、图11b、图12b)；当荷载达到极限承载力时，CLL9020系列和CLL6020系列试件发生了整体弯曲失稳，并且CLL9020系列角钢柱在变形截面处产生了较大的折曲.

图10 长度为900 mm的角钢柱屈曲模式

图11 长度为1 500 mm的角钢柱的屈曲模式

图12 长度为2 100 mm的角钢柱屈曲模式

2.2 试验结果与分析

各复杂卷边等肢角钢轴压试件试验极限承载力Pt见表3.由表3可知，CLL6020和 CLL9020系列试件随着试件长度增加，宽厚比较小的试件其屈曲模式由畸变屈曲变成畸变和整体弯曲相关屈曲；对于宽厚比较大的试件，屈曲模式由局部和畸变相关屈曲变成了局部、畸变和整体相关屈曲.试件承载力随长度的增加而下降.

表3 试件试验和有限分析屈曲模式和承载力对比

CLL6020系列试件的荷载-竖向位移曲线见图13.由图13可知，对于CLL6020-1500(图13a)和CLL6020-2100(图13b)试件，在最大荷载之前曲线呈线性增长，临近最大荷载时，随着弯曲的发生，曲线进入非线性阶段，达到极限荷载后荷载陡降，试件破坏.对于CLL6020-900(图13c)和CLL6020-400(图13d)试件，在加载初始阶段整体刚度基本不变，曲线呈线性增长，随着荷载的增大进入非线性阶段，达到最大荷载后，荷载缓慢减小.

图13 CLL6020系列荷载-轴向位移曲线

3 有限元分析

3.1 有限元模型的建立

采用大型通用商业有限元软件ABAQUS 6.14建立冷弯薄壁复杂卷边等肢角钢轴压试件的有限元分析模型，试件长度和横截面尺寸取试件实测尺寸，材性值采用材性试验平均值.采用S4R壳(shell)单元和理想弹塑性模型.400 mm、900 mm和1 500 mm长试件采用10 mm×10 mm网格尺寸， 2 100 mm长构件采用20 mm×20 mm网格尺寸.试件两端固结，在加载端约束5个自由度(2个平动自由度和3个转动自由度)，释放UZ纵向自由度，在另一端完全固定(约束3个平动自由度和3个转动自由度).在加载端截面形心的耦合点RP-1处施加竖向位移.为了更加真实地模拟试件，引入测量的初始几何缺陷，缺陷值取整体、畸变、局部初始几何缺陷的最大值.有限元分析分为两步：第一步为特征值屈曲分析，其第一阶屈曲模态作为试件的初始缺陷形状；第二步是非线性分析，采用Mises屈服准则，弧长法求解，得到试件屈曲模态和极限承载力.

3.2 有限元结果分析

有限元分析结果见表3，表明有限元分析的极限承载力与试验承载力较吻合，试验承载力与有限元分析承载力比值的平均值为1.01，变异系数为0.08.有限元分析与试验屈曲模态对比见图14，有限元分析屈曲模态与试验基本一致.图15为试件与有限元模拟分析的荷载-轴向位移曲线对比，由此可知试验与有限元分析曲线吻合较好.对比结果表明本文建立的冷弯薄壁复杂卷边等肢角钢有限元分析模型能够较好地模拟轴压复杂卷边等肢角钢构件的屈曲模式、极限承载力以及荷载位移曲线.

图14 试验与有限元屈曲模式对比

图15 试验与有限元分析荷载-轴向位移曲线对比

4 建议计算方法

4.1 直接强度法

北美规范[17]采用直接强度法计算构件承载力，轴压试件的承载力P取局部和整体相关屈曲承载力P与畸变屈曲承载力Pnd的最小值.

局部和整体相关屈曲承载力按下式计算：

(1)

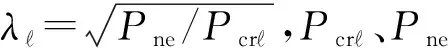
弹性局部屈曲承载力可通过有限条软件CUFMS计算得到，整体屈曲承载力Pne按下式计算：

Pne=AgFn，

(2)

其中Fn按下式计算：

(3)

畸变屈曲承载力按下式计算：

(4)

4.2 有效宽度法

《冷弯薄壁型钢结构技术规范》(GB 50018-2002)[18]中轴心受压构件稳定承载力按下式计算：

N=φAefy，

(5)

式中：Ae是有效截面面积，φ是轴心受压构件的稳定系数，计算时其长细比取弯扭屈曲换算长细比λw和对y轴的长细比λy的最大值，fy为钢材屈服强度.

4.3 建议计算方法

采用直接强度法和有效宽度法计算得到轴心受压复杂卷边角钢试件承载力Pz和Py(表4).由表4可知：规范直接强度法和有效宽度法计算结果偏于保守，主要是因为计算轴压复杂卷边等肢角钢承载力时，采用弯扭屈曲换算长细比考虑构件整体扭转，而畸变屈曲与扭转屈曲是一致的，导致构件扭转被重复考虑.为此建议在计算构件整体屈曲时忽略扭转的影响，仅计算弯曲屈曲.从而采用直接强度法计算时，公式(3)中Fcre取复杂卷边等肢角钢两形心主轴整体弯曲屈曲应力的最小值.采用有效宽度法计算时，当计算轴心受压构件的稳定系数时，其长细比取两形心主轴整体弯曲屈曲长细比λx和λy的最大值.采用建议计算方法计算所得轴压角钢构件承载力Pza和Pya见表4.由表4可知，采用修正后的直接强度法和有效宽度法计算构件承载力与试验结果较吻合，因此修正后的直接强度法和有效宽度法计算轴心受压复杂卷边等肢角钢构件承载力是精确可行的.

表4 试验值、规范方法以及修正设计方法及计算承载力对比

5 结论

(ⅰ)16根冷弯薄壁复杂卷边等肢角钢试件轴压试验表明，宽厚比较小、长细比较小的试件发生畸变屈曲，而宽厚比较小、长细比较大的试件发生畸变和整体弯曲的相关屈曲；宽厚比较大、长细比较小的试件发生局部和畸变相关屈曲，而宽厚比较大、长细比较大的试件发生局部、畸变和整体弯曲相关屈曲.试件承载力随长度的增加而下降.

(ⅱ)用所建立的ABAQUS有限元分析模型分析的试件极限承载力、屈曲模式、荷载轴向压缩位移曲线与试验吻合较好，表明建议的有限元分析模型用于冷弯薄壁复杂卷边等肢角钢柱的屈曲性能分析是可行的.

(ⅲ)由于畸变屈曲与扭转屈曲是一致的，采用规范规定的直接强度法和有效宽度法计算复杂卷边等肢角钢轴压承载力时规范方法过于保守.为此提出在计算整体屈曲时忽略扭转屈曲的建议方法，建议的直接强度法和有效宽度法计算结果较为准确，表明建议方法可用于冷弯薄壁复杂卷边等肢角钢轴压承载力的计算.