考虑被超非机动车偏移减速的改进社会力模型

2023-01-14张蕊郝嘉田张士杰程世达

科学技术与工程 2022年34期

张蕊，郝嘉田，张士杰，程世达

(1.北京建筑大学土木与交通工程学院，北京 100044； 2.北京建筑大学首都世界城市顺畅交通协同创新中心，北京 100044； 3.北京建筑大学北京市城市交通基础设施建设工程技术研究中心，北京 100044)

超车事件是衡量非机动车道路交通服务水平的重要指标[1]，常用非机动车超车事件数来获得非机动车换算系数[2-4]，这些基于统计学的研究方法需要数据样本量大，通过观测的方法难以全面获取[5]，通过建立能够反映非机动车混合流主要行为特征的非机动车微观仿真模型，获取多样化的非机动车运行数据用以研究非机动车换算系数是一种可替代的方法。

电动自行车超越自行车是非机动车混合流重要的交通行为特征，倪颖等[6]基于舒适空间理论构建了动机—决策—执行三层框架描述超车行为。Liang等[7]建立了自行车的心理—生理力学模型，使骑行者遇障碍物时通过轨迹偏移实现超越；严巧兵[8]在社会力模型中加入超越力，实现非机动车的主动超越行为。以上研究仅考虑了超车过程中超车车辆的行为，Li[9]将非机动车超车类型划分为自由超车、临贴超车两种情况，研究发现临贴超车过程中由于车辆行驶空间有限，超车行为对被超车辆运行干扰较大。Chuang等[10]分析得出超车干扰会增加被超车骑行者的心理负担，进而其速度、位置、行驶方向均发生变化。陈小鸿等[11]分析了超车过程中被超自行车横、纵向加速度的变化。Minh等[12]和Khan等[13]通过实测数据研究了超车过程中超车车辆与被超车辆间的速度差异以及两车横、纵向距离变化情况。上述研究均通过实测获得了超车过程中被超车辆避让特征，因此在建立非机动车超车模型时，应考虑被超车辆的影响。

因此，现拟建立临贴超车情况下被超车辆社会力模型，改进被超车辆排斥力与驱动力实现其偏移避让和减速避让行为，通过仿真实验获得非机动车运行数据，据此计算非机动车换算系数。

1 考虑被超车辆行为特征的改进社会力模型

(1)

式(1)中：→为力的方向。

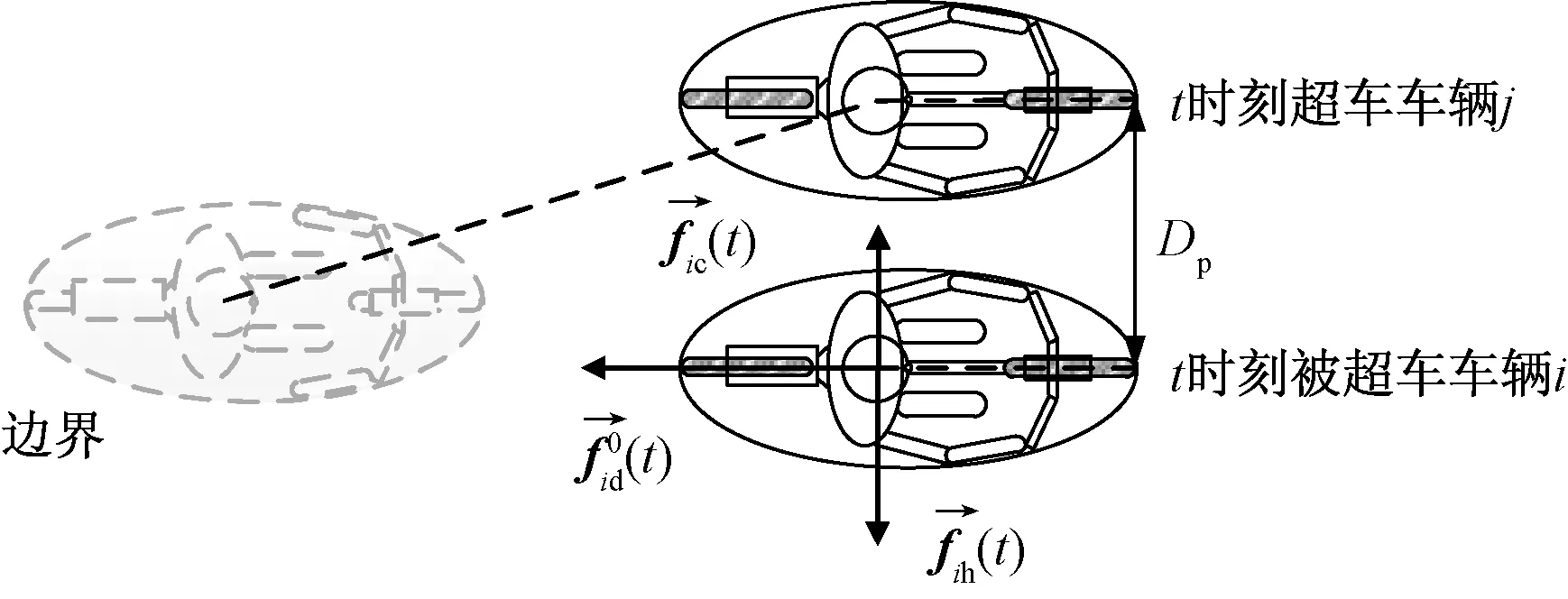
图1 被超车辆受力分析Fig.1 Force analysis of the overtaken vehicles

1.1 改进排斥力

实测发现，临贴超车过程中超车及被超车辆均会偏离各自行驶轨迹，被超车辆对于超车干扰的感受不同于超车车辆，表现为二者最大横向偏移距离的不同。实测不同速度差下两车并排骑行至超车结束阶段最大横向偏移距离如表1所示。

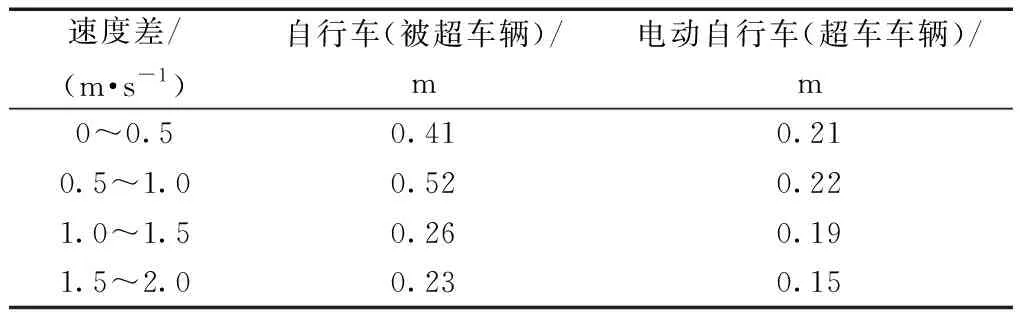
表1 最大横向偏移距离平均值Table 1 Average of maximum lateral shift distance

被超车辆受超车干扰程度可用动能权重系数μ表示，动能指物体由于运动而具有的能量，是衡量冲突危险性的重要指标。超车车辆具有较大动能，临贴超车过程中若发生碰撞事故会对小动能被超车辆产生较大影响，因此被超车辆横向偏移距离大于超车车辆。两车速度差较大时，被超车辆还未感知超车干扰超车过程便已结束，因此偏移距离较小。动能权重系数μ根据被超车辆动能与两车总动能之比求得，即

(2)

式(2)中：mi、mj分别为自行车、电动自行车与骑行者的总质量，根据调查，自行车与骑行者平均总质量按85 kg计，电动自行车与骑行者平均总质量按100 kg计；vi(t)、vj(t)分别为自行车i与电动自行车j的速度。

社会力模型中将骑行者想要与其他车辆保持一定距离的心理表示为排斥力[14]，小动能被超车辆对超车过程中两车横向距离的变化更加敏感，因此其所受排斥力大小与超车车辆不同。引入动能权重系数对两车距离重新计算，被超车辆所受排斥力为

(3)

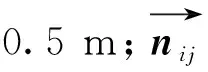
1.2 改进驱动力

调查发现，临贴超车过程中超车车辆与被超车辆并排骑行车头纵向间距较小时，被超车辆骑行者不舒适感增加，进而选择减慢自身速度达到远离超车车辆的目的。应用非机动车社会力模型[14]仿真计算不同车头间距下被超车辆纵向加速度，与实测数据对比，如表2所示，发现车头纵向间距较小时被超车辆所受合力为其提供的加速度不能满足其减速避让需求。

在驱动力作用下车辆运行速度不断向期望速度靠近，本文通过改进期望速度实现被超车辆减速避让行为。统计被超车辆期望速度与两车车头间距之间的关系如图2所示。

图2中，两车车头间距小于临界最小车头间距时，被超车辆期望速度随车头间距的减小而降低，两者间关系可拟合为二次方程形式。当两车车头间距大于临界最小车头间距时，被超车辆受超车干扰影响程度降低，由减速避让转变为追求最大期望速度。本文研究中采用分段函数形式描述不同车头间距下被超车辆期望速度的变化，即

(4)

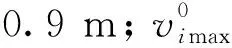
表2 仿真及实测被超车辆纵向加速度

图2 被超车辆期望速度与车头间距的关系Fig.2 Relationship between the desired speed of the overtaken vehicle and the space headway

据此改进被超车辆驱动力为

(5)

2 模型验证

为验证上述所建模型的有效性，本文利用Python语言进行计算机仿真。依照实测交通环境建立宽3.5 m的机非物理隔离非机动车路段，无机动车、行人及逆行非机动车干扰。调查时段电动自行车交通量1 108 辆/h，自行车交通量738 辆/h。记录每个仿真时间步长(0.05 s)内的非机动车混合流速度、密度及车辆坐标，为保证仿真实验数据的完备性和准确性，去除未形成稳定流阶段的仿真数据并进行多次重复实验，提取发生临贴超车所对应的密度(0.07～0.30 辆/m2)下的仿真数据验证模型有效性。

2.1 基本图验证

将仿真所得非机动车流速度-密度关系与实测数据进行对比，如图3所示，验证所建微观模型反映的宏观现象的真实性。改进后仿真模型速度-密度趋势与调查数据趋势变化一致，证明改进模型能够再现非机动车流基本图。

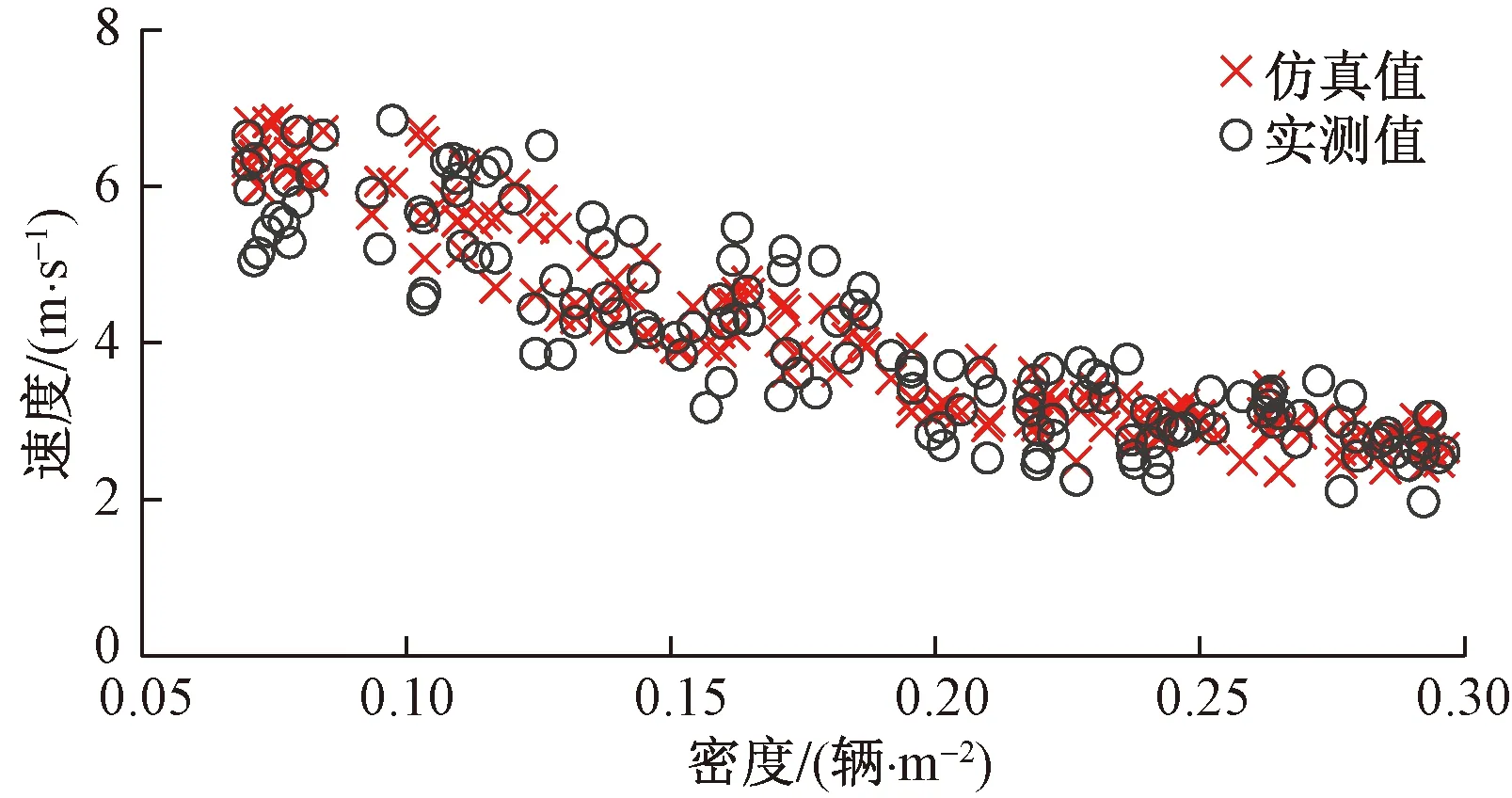
图3 仿真及调查非机动车速度-密度关系Fig.3 Speed-density diagram of non-motorized vehicles by investigation and simulation

进一步对调查及仿真数据进行95%置信度独立样本T检验，发现方差及均值显著性为0.335及0.993均大于0.05，说明实测数据与仿真数据无显著性差异。

2.2 被超车辆骑行行为分析

仿真时间13.4～16.5 s存在超车行为，如图4所示，提取此阶段内超车与被超车辆速度、位置坐标等仿真数据，绘制二者骑行轨迹如图5所示。观察图4和图5，仿真时间t=13.4 s时，1号电动自行车企图超越前方2号自行车，两车并排行驶时横向间距为0.88 m，超车类型为临贴超车。此时1号、2号车辆速度分别为5.4、4.7 m/s。15.2 s时，2号被超车辆感知到超车干扰，在排斥力的作用下逐渐偏离原行驶轨迹，在驱动力的作用下速度逐渐减至4.3 m/s。16.5 s临贴超车结束，2号被超车辆最大横向偏移距离为0.51 m，此时两车横向距离为1.61 m。

为进一步验证仿真与实测数据的差异性，选取不同速度差下被超车辆最大横向偏移距离以及不同车头间距下被超车辆纵向加速度仿真数据，与实测数据对比发现误差均在15%以内，如表3和表4所示，仿真结果与实测数据具有良好的一致性。

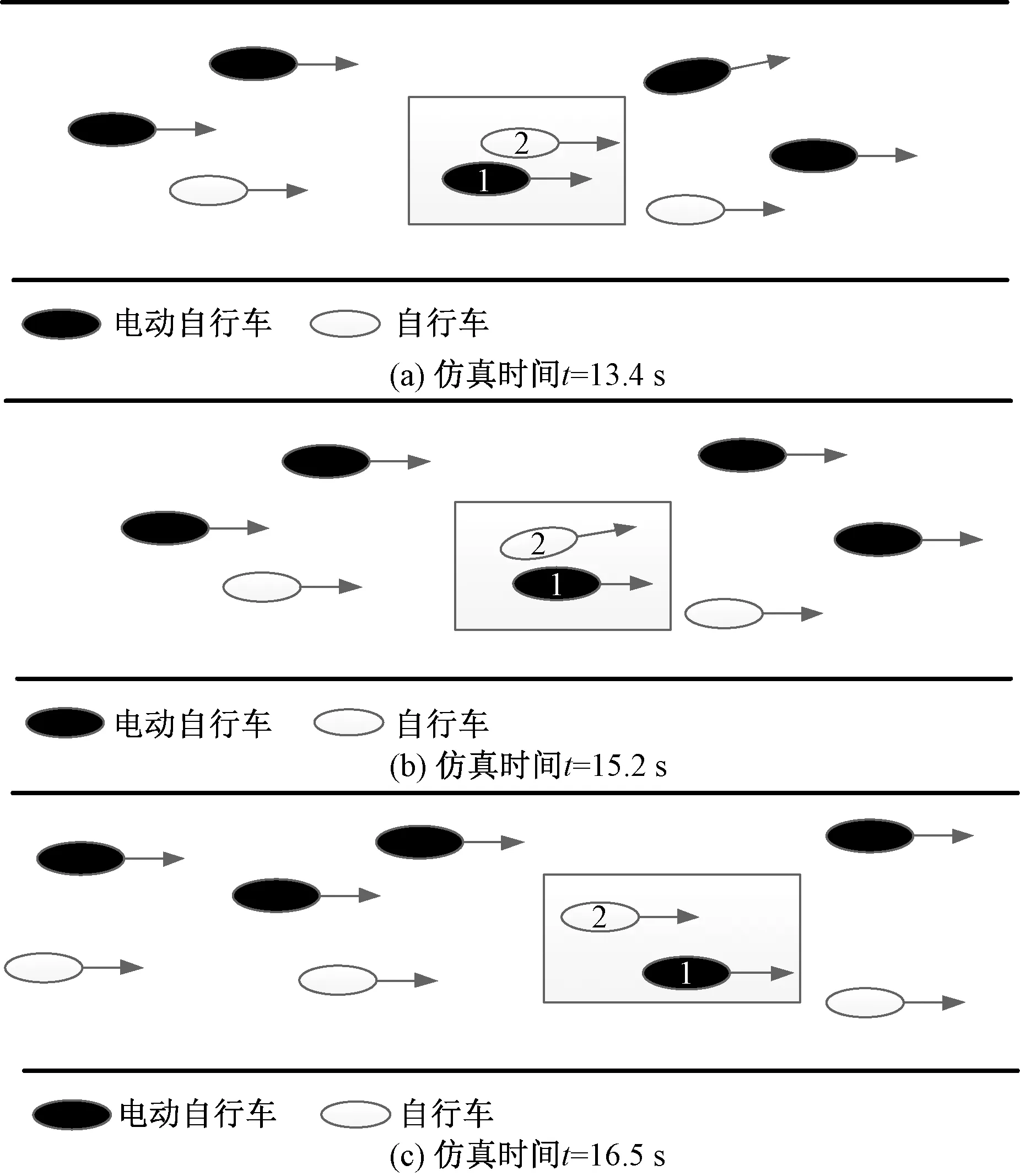
图4 被超车辆避让行为仿真情景图Fig.4 Avoidance behavior of overtaken vehicle simulation scenario

图5 骑行者仿真轨迹示意图Fig.5 Sketch of riders’ simulation trajectory

表3 最大横向偏移距离误差分析Table 3 Error analysis of maximum lateral shift distance

表4 纵向加速度误差分析Table 4 Error analysisof longitudinal acceleration

综合上述研究分析，所建模型能够还原被超车辆的行为特征，可进行非机动车换算系数等相关应用研究。

3 非机动车换算系数研究

电动自行车相对于自行车的换算系数[2]可定义为:在一定的道路和交通条件下，电动自行车可以用一定量的自行车来代替，此代替量即为电动自行车相对于自行车的换算系数。Chen等[5]发现，非机动车流中电动自行车比例是影响换算系数的重要因素，电动自行车混入比例低于25%时的实测数据难以获得，因此相应换算系数缺失。本文构建与Chen等[5]相同的交通环境，通过所建非机动车微观模型仿真获取不同电动自行车比例下(0～25%、25%～50%、50%～75%、75%～100%)的非机动车超车事件数，建立电动自行车密度、自行车密度与超车数之间的关系模型[4]，如表5所示。电动自行车密度变化对超车数的影响值与自行车密度变化对超车数的影响值之比，即为换算系数计算方法，如式(6)所示。

(6)

式(6)中：nTc为电动自行车相对于自行车的换算系数。

表5 非机动车超车事件数模型Table 5 Non-motorized vehiclesovertaking event model

将表5中非机动车超车事件数模型回归结果代入式(6)，可得到不同电动自行车比例下的非机动车换算系数，计算结果如表6所示。

表6 不同电动自行车比例下的换算系数Table 6 Conversion coefficient under differentproportions of electric bicycles

将本文得到的25%～50%、50%～75%、75%～100%电动自行车混入比例下的非机动车换算系数值与Chen等[5]研究取值进行对比，如表6所示，二者最大差值为6.9%，表明通过仿真所得的换算系数值与通过实测数据所得换算系数值具有良好的一致性，也从另一角度验证了上述所建改进社会力模型的有效性。因此在缺少实测数据的情况下，通过模型仿真获取数据作为替代方法，计算电动自行车混入比例低于25%时的换算系数值为0.92具有合理性。