两种OFDM信号的雷达探测性能研究

宋 瑶， 唐裕峰， 武浩正， 靳 标

(江苏科技大学，江苏 镇江 212000)

0 引言

OFDM信号具有抗干扰、低截获等性能优势，是雷达通信一体化系统常用的发射波形之一[1]。但是，OFDM信号存在两大缺陷：第一，峰值平均功率比(Peak-to-Average Ratio，PAR)较高，当雷达发射机工作在非线性区域时，信号会产生非线性失真和谐波，造成明显的频谱扩展和带内信号畸变，导致射频放大器功放的效率降低;第二，大多数OFDM信号的模糊函数呈图钉状，为“多普勒敏感”信号，当匹配滤波器存在细微多普勒失配，将会导致滤波器性能迅速下降。研究表明，选择适当的载波调制序列是解决这两个问题的关键[2-5]。

ZC序列(Zadoff-Chu序列)具有良好的自相关特性和呈“斜刀刃”型的模糊函数特性。文献[6]将ZC序列作为同步训练序列，有效降低了水声信道产生的载波频率频移，从而消除来自不同方向的噪声对信道产生的干扰；文献[7]利用ZC序列对多径衰落信道进行估计，解决了残留频偏的问题，提高了高速移动宽带通信系统的定时准确率;文献[8]通过比较 ZC-OFDM信号和Gold-OFDM信号在不同信噪比条件下的通信误码率发现，ZC序列可以通过对数据符号进行编码提高通信性能。

Oppermann序列同样具有良好的自相关特性和互相关特性，是扩频通信中常用的一种序列。文献[9]将加权脉冲序列与Oppermann序列作为权值，对给定的系统约束进行特定的多目标优化，实现了通信系统中的多址访问；文献[10]给出了Oppermann序列与加权脉冲序列的交叉模糊函数的解析表达式，推导了自模糊函数表达式，并证明了两种模糊函数的差异性。

基于ZC序列和Oppermann序列的一些优秀特性，本文通过对ZC序列和Oppermann序列调制的OFDM信号的自相关、循环自相关、峰均比、模糊函数和多普勒容限等特性进行比较，分析了两种信号作为雷达通信一体化发射波形的可行性。

1 序列的定义及其性质

1.1 两种序列的定义

1.1.1 ZC序列的定义

ZC序列属于恒包络零自相关序列 (Constant Amplitude Zero Auto-Correlation，CAZAC)，其定义为

(1)

式中:k=0,1,2,…,N-1；u∈N+，为序列的根序列;N为序列的长度;对于任意ZC序列，在长度N和根序数u的取值确定的情况下，便可确定根序列;u的取值需要与N互质，且在N确定以后，u能够唯一确定一个ZC序列。一般情况下为方便计算，q取值为0，可改写为

Zu(k)=exp[-jπuk(k+c+2q)/N]

(2)

式中：k=0,1,2,…,N-1；c=Nmod 2。

1.1.2 Oppermann序列的定义

一个码长为N的Oppermann序列为uk=[uk(0)，uk(1)，…，uk(N-1)]，其中的每个元素满足

(3)

式中:1≤k≤N-1，0≤i≤N-1，i与N互质，N为质数；m，n，p为序列的3个参数，且均为实数。

1.2 两种序列的性质对比

1.2.1 自相关特性

离散时间序列的自相关函数定义为

(4)

式中：b(k)为调制序列;b*(k+n)为b(k)时延信号的共轭。

将式(2)代入式(4)可得，ZC序列的自相关函数为

(5)

由式(3)可知，当m，n和p为固定值时，所有序列具有相同的自相关函数。当p=1时，Oppermann序列自相关函数的大小仅取决于n，其定义为

(6)

式中，l为序列的离散循环移位。为了控制参数数量，一般情况下取p=1。

图1给出了N=61，u=1时的ZC序列与N=61，m=1，p=1，n=2.007 2时的Oppermann序列的自相关函数。

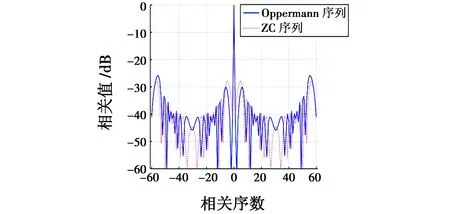
图1 两种序列的自相关函数Fig.1 Autocorrelation function of two sequences

从仿真结果可以看出，两种序列都具有集中的主瓣，但ZC序列的第一副瓣高于Oppermann序列。

1.2.2 循环自相关特性

大部分雷达信号都具有循环平稳特性，这种循环平稳特性通常用循环自相关函数来表示。

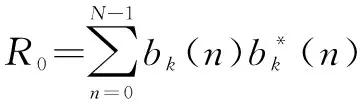
(7)

ZC序列的循环自相关函数可表示为[11]

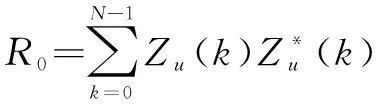
(8)

式(8)经推导得[12]

(9)

Oppermann序列的循环自相关函数可表示为

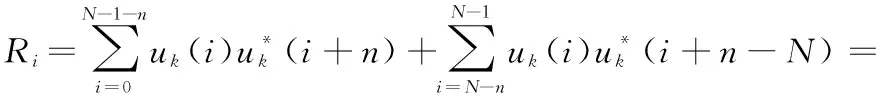
(10)

图2给出了N=60，u=1的ZC序列与N=60，m=1，p=1，n=2.007 2的Oppermann序列的循环自相关函数。从仿真结果可以看出，ZC序列具有良好的循环自相关特性且自相关峰值尖锐，对于任意ZC序列与其循环移位a位后的序列互不相关(a≠0)；Oppermann序列在长度N=50时具有较好的自相关性，但互相关性较差。通过对比分析可得，ZC序列的循环自相关性优于Oppermann序列。

图2 两种序列的循环自相关函数Fig.2 Cyclic autocorrelation function of two sequences

1.2.3 峰均比特性

峰值平均功率比(Peak-to-Average Ratio，PAR)，简称峰均比。一般情况下，峰均比指最大瞬时功率与平均功率的比值，定义为

(11)

离散序列的实部和虚部的峰均比分别为

(12)

(13)

式中：RPAR(real)为峰均比实部;RPAR(imag)为峰均比虚部。

将式(1)用欧拉公式展开可得

Zu(k)=exp[-jπuk(k+c+2q)/N]=cos[πuk(k+

c+2q)/N]-jsin[πuk(k+c+2q)/N]。

(14)

ZC序列的实部和虚部的峰均比分别为

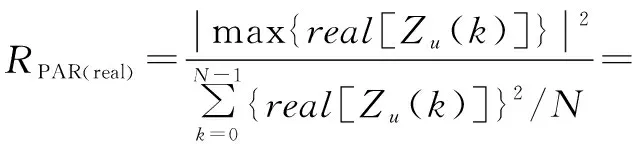
(15)

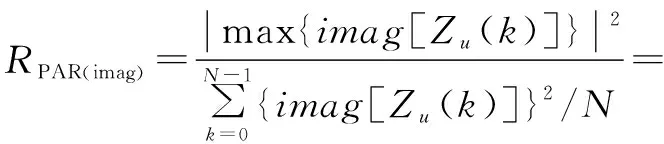
(16)

将式(3)用欧拉公式展开，可得

(17)

Oppermann序列的实部和虚部的峰均比分别为

(18)

(19)

当k为奇数，i为偶数时，Oppermann序列实、虚部的峰均比可分别表示为

(20)

其他情况时，Oppermann序列实、虚部的峰均比可分别表示为

(21)

图3给出了N=10 000，u=1的ZC序列与N=10 000，m=1，p=1，n=2.007 2的Oppermann序列的峰均比特性。

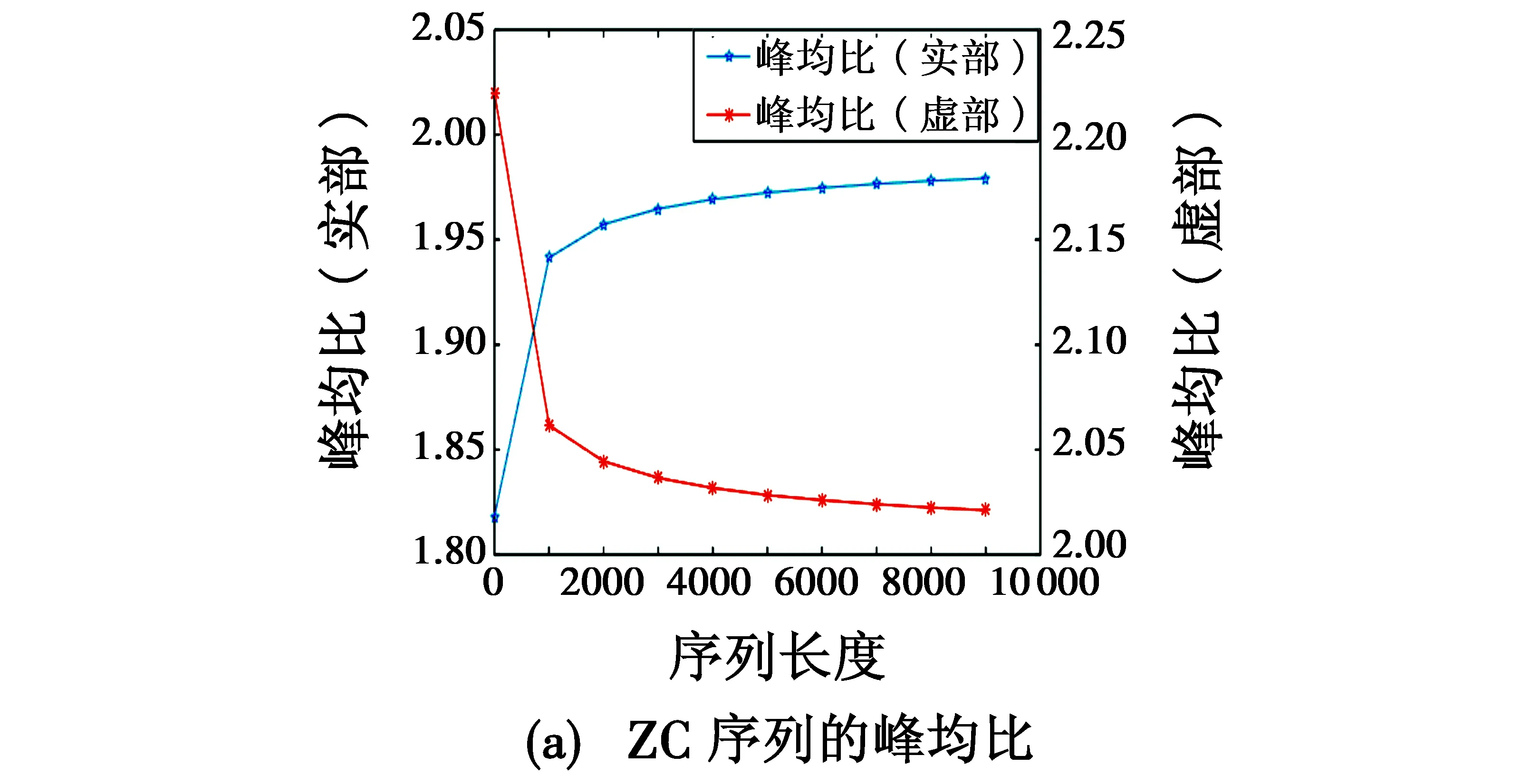
图3 两种序列的峰均比特性比较Fig.3 Comparison of peak to averageratio characteristics of two sequences

由图3可知，随着序列长度的增加，ZC序列实部的峰均比值逐渐增大，最大值接近于2，虚部峰均比值逐渐减小，最后趋近于1.82;但Oppermann序列实部峰均比值和虚部峰均比值都逐渐增大，实部峰均比值趋近于6，虚部峰均比值趋近于5.7。因此，ZC序列的峰均比特性优于Oppermann序列，更有利于雷达功率放大器工作在饱和区域。

2 两种信号的雷达探测特性研究

为了充分验证两种序列调制的OFDM信号的探测性能，本文将ZC-OFDM信号和Oppermann-OFDM信号的模糊函数、多普勒容限特性进行对比，验证了两种信号作为雷达探测信号的可行性。

2.1 模糊函数分析

OFDM信号提供了一种在频域上设计波形、时域上输出波形的DFT数字调制方式。

OFDM信号的数学表达式为

(22)

式中:bk是调制序列，为第k路子信道中的复输入数据;fk=f0+kΔf，f0为起始频率，Δf为频率间隔。

由式(22)可知，雷达脉冲序列的复包络可表示为

(23)

在雷达接收端，回波信号相对发射信号会引起时延和多普勒频移。假设信号波形的时延为τ，多普勒频移为fd，信号在传播过程中衰减为原来的A倍，则信号的回波信号可表示为

(24)

模糊函数是雷达探测波形分析的重要工具，通过对信号波形的模糊函数分析，可以得到信号波形的距离分辨率、多普勒分辨率及多普勒容限特性。模糊函数的定义为

(25)

式中，E为信号的总能量。

式(25)一般表示连续时间信号的模糊函数，离散时间序列的模糊函数表示为

(26)

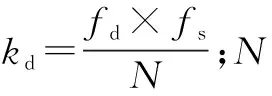
由于ZC序列是离散序列，由式(26)可知ZC-OFDM信号的模糊函数为

(27)

因为Oppermann序列和ZC序列同为离散序列，所以由式(26)知Oppermann-OFDM信号的模糊函数可表示为

(28)

图4所示为ZC-OFDM和Oppermann-OFDM信号的模糊函数。由图4可知，ZC-OFDM信号的模糊函数和Oppermann-OFDM信号的模糊函数类似，呈现出角度不同的“斜刀刃”特性，但ZC-OFDM信号的模糊函数具有较低的旁瓣，因此具有更好的探测性能。两种信号的模糊函数切面对比分析如图5所示。由图5可知，ZC-OFDM信号模糊函数的多普勒切片和时延切片具有相对较窄的主瓣宽度，具有更高的时延和多普勒分辨性能。

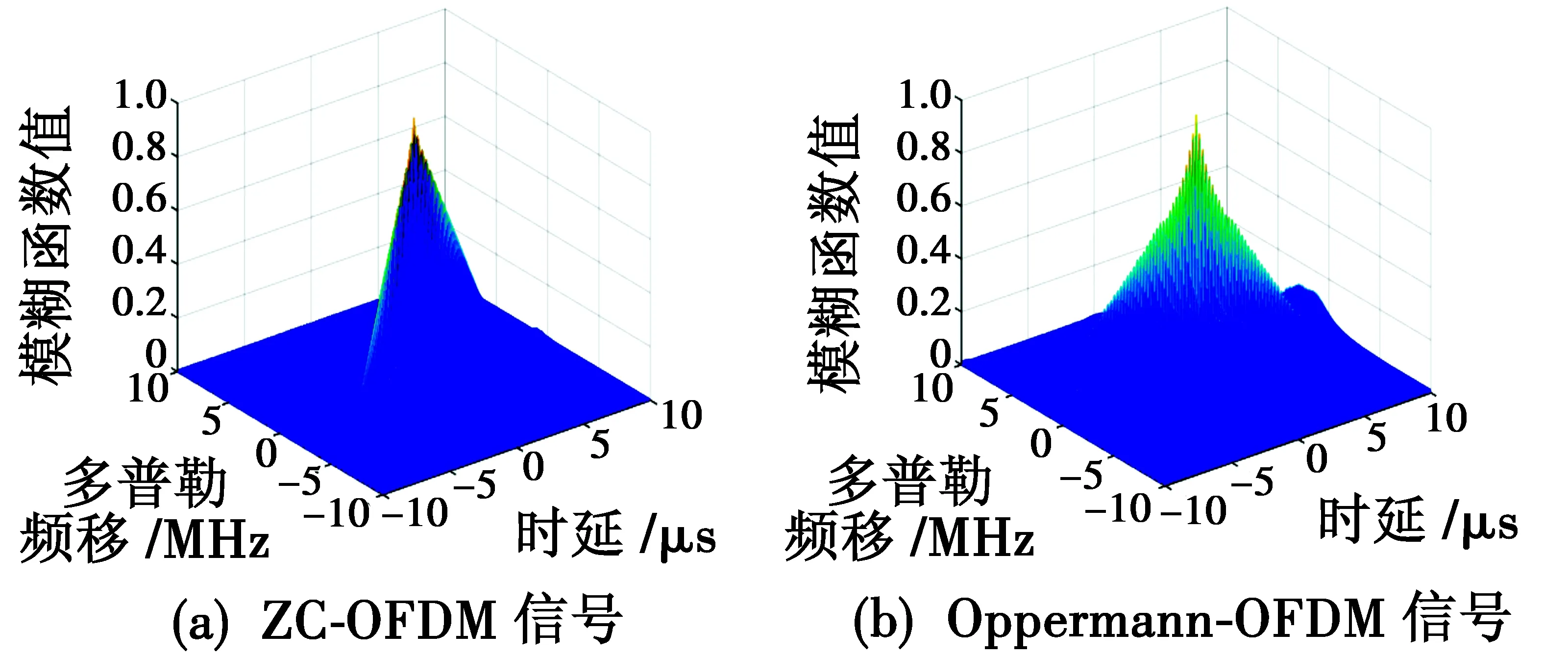
图4 两种OFDM信号的模糊函数Fig.4 Ambiguity functions of two OFDM signals

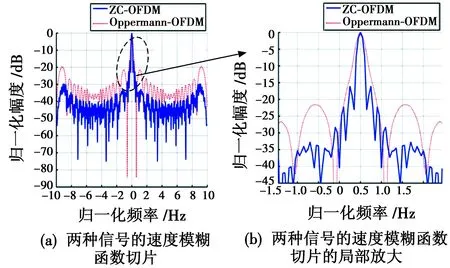
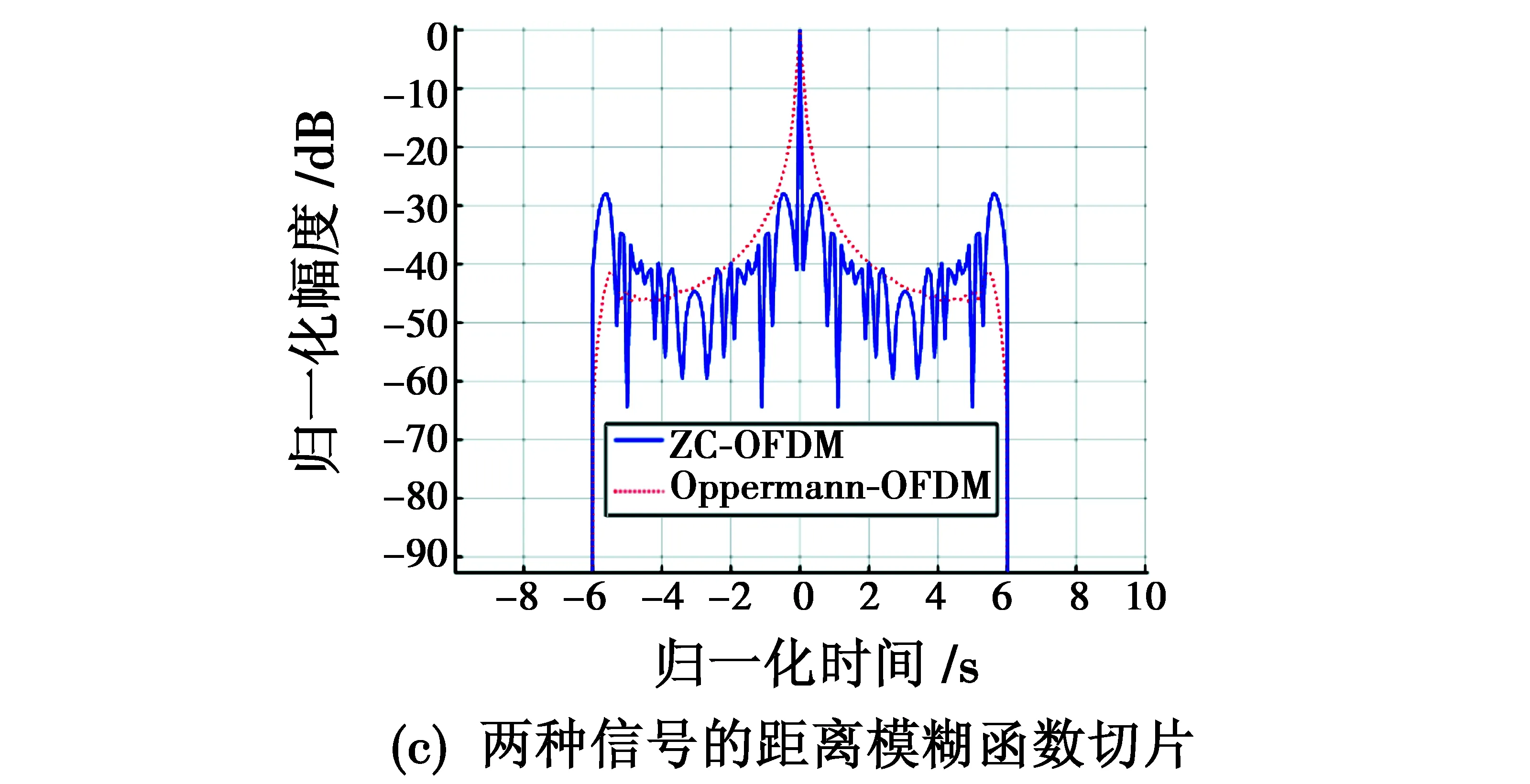
图5 两种OFDM信号的模糊函数特性Fig.5 Ambiguity function characteristics of two OFDM signals

2.2 多普勒容限特性研究

在相同脉宽条件下，回波信号的脉压增益下降到最低容许程度时的多普勒频移称为多普勒容限特性。多普勒容限检测函数为

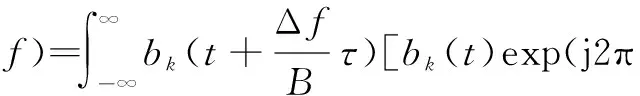
(29)

式中，B为信号带宽。

对式(29)两边以Ts(1/fs)为间隔周期进行采样，令t=nTs，则有

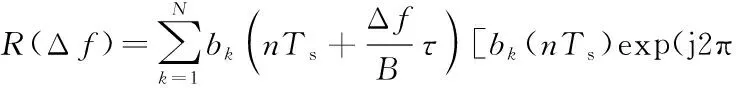
(30)

可得离散多普勒容限检测函数R(m)为

(31)

由式(31)得ZC-OFDM信号的多普勒容限检测函数为

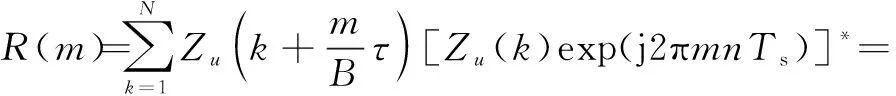
(32)

同理，由式(31)得Oppermann-OFDM信号的多普勒容限检测函数为

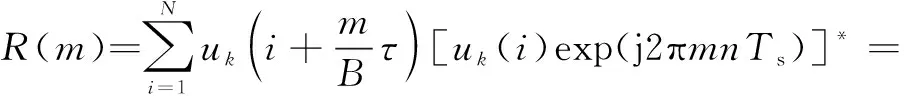
(33)

根据式(32)和式(33)，在同等采样率fs=20 MHz，带宽B=10 MHz，时宽长度t=10 μs的条件下，两种OFDM信号的多普勒容限特性如图6所示。

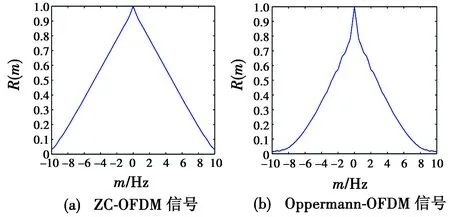
图6 两种OFDM信号的多普勒容限特性Fig.6 Doppler tolerance characteristics of two OFDM signals

由图6可知，ZC-OFDM信号和Oppermann-OFDM信号具有相似的多普勒容限特性，但ZC-OFDM信号的多普勒容限特性曲线比较平滑，即ZC-OFDM信号具有更好的多普勒容限特性。

3 结论

通过对ZC序列和Oppermann序列调制的OFDM信号波形特性的对比分析表明ZC-OFDM信号比Oppermann-OFDM信号具有低峰均比特性和更好的多普勒容限特性，ZC-OFDM信号和Oppermann-OFDM信号具有相同的“斜刀刃”型的模糊函数特性、较好的速度分辨率特性和距离分辨率特性，但是ZC-OFDM信号的模糊函数特性及多普勒容限特性相比于Oppermann-OFDM信号具有更好的探测性能。但是，由于两种OFDM信号具有相同的“斜刀刃”型的模糊函数特性，因此两种信号都存在距离和多普勒频移耦合的现象。