几何效应的可拓知识表示研究

葛标标，杨春燕，汤龙

（1.广东工业大学 可拓学与创新方法研究所，广东 广州 510006;2.广东工业大学 机电工程学院，广东 广州 510006;3.南京信息工程大学 人工智能学院，江苏 南京 210044）

知识表示、知识获取和知识处理是知识工程 的三大支柱，而其核心是知识表示。知识表示是对知识的一种描述或者一种约定，是计算机可以接受的用于描述知识的数据结构。目前人工智能常用的知识表示方法有谓词逻辑、产生式知识表示、语义网络知识表示、框架表示、模糊逻辑知识表示等，但是它们也有各自的局限性[1-2]。

可拓学是以矛盾问题为研究对象，以形式化的模型，探讨事物拓展的可能性以及开拓创新的规律与方法的一门新学科[3-4]。可拓学建立了能够描述物、事和关系的可拓模型，该模型可以作为可拓知识表示的基础。可拓学的逻辑基础是可拓逻辑，研究了矛盾问题转化和推理的规律[4]。文献[5]提出了一种基于事元理论的机械运动系统行为知识表示；文献[6]针对现有计算机辅助工艺过程设计（computer aided process planning,CAPP）系统知识化表示不足，运用可拓学理论，建立了一种成衣制造可拓知识表达模式；文献[7]提出了可拓知识作为元知识的一种新表现形式；文献[8]基于可拓学中的规则，提出了一种可拓规则的知识表示方法；文献[9]提出了可拓信息—知识—策略的形式化表示体系，为计算机生成解决问题的策略提供了基础理论和方法；文献[10] 运用可拓模型表示机械概念结构的特征信息、连接约束信息、拓扑结构变换信息；文献[11]将可拓本体理论与知识库技术相融合，构建面向复杂产品方案设计及推理的可拓本体知识库系统；文献[12]提出一种面向生命周期的低碳设计可拓知识建模方法。

科学效应是阿奇舒勒通过对世界范围内的专利分析总结得出的一种解决问题的科学原理，是将效应中有关的量互相联系起来的各领域定律，主要面向功能问题的求解[13]。求解过程中，人们从具体的问题抽象出解决该问题的功能；根据实现功能查询科学效应库，找出解决问题的一个或者多个科学效应，再筛选出合适的科学效应，并将科学效应具体化得到功能原理解。目前，已经总结出的科学效应超过10 000 条，每条科学效应的具体应用又多种多样。为了高效地使用科学效应知识，快速获得解决矛盾问题的创新解，构建科学效应知识库是十分必要的，而科学效应的知识表示是构建科学效应知识库的基础。针对科学效应的知识表示已经有较多的研究，文献[14]以化学领域为例，提出了基于领域本体科学效应的知识表示；文献[15]提出基于Prolog 的科学效应知识表示；文献[16]提出了一种形式化表达物理效应知识的方法；文献[17]提出了基于本体的科学效应知识表达；文献[18-19]建立了基于本体论方法的物理效应知识表示模型，并且提出了一种用于更新物理效应数据库的多智能模型；文献[20]提出了基于知识粒度的科学效应；文献[21-22]基于知识图谱，提出一种科学效应知识库的构建方法。但是这些知识表示对科学效应中输入与输出的变换关系均未详细探讨，也没有对输入与输出进行形式化和定量化的知识表示。

本文从可拓学角度对科学效应中的几何效应机理进行分析，认为几何效应的输入与输出具有相关关系，输入的变换会导致输出的变换。因此根据可拓学中的可拓模型、发散规则、相关规则、可拓变换的蕴含规则、传导变换规则以及相关型知识，提出了一种新的几何效应的可拓知识表示方法，并以双曲面搅拌器设计为例，验证该方法的可行性。

1 可拓知识表示与科学效应

1.1 基于拓展规则的知识表示

一些简单的知识，可以直接用基元表示，但是一些相对复杂的知识包含基元之间的关系，因此需要用基于可拓规则的基元关系式来表达。可拓规则包括拓展规则、共轭规则、传导规则、基元的逻辑运算规则、变换的运算规则等[1]。基于拓展规则的知识表示，包括发散型知识、相关型知识、蕴含型知识和可扩型知识，统称为拓展型知识[23]。由于科学效应中几何效应的输入与输出具有相关关系，输入的变换会导致输出的变换，主动变换与传导变换之间具有蕴含关系。在实施主动变换前，首先要对待实施主动变换的基元进行发散分析，以获取变换的各种可能途径。但是限于篇幅，本文重点介绍相关型知识，其他类型的知识请参考文献[23]。

相关型知识是根据可拓逻辑中的相关规则得到的表示基元间相关关系的知识，主要包括如下类型：

1）两个基元B1=(O1,c1,v1)与B2=(O2,c2,v2)双向（互为）相关的相关型知识的一般表达式为B1～B2。

2）两个基元B1=(O1,c1,v1)与B2=(O2,c2,v2)为单向相关的相关型知识的一般表达式为B1B2。

3）一个基元B=(O,c,v) 与多个基元B1=(O1,c1,v1),B2=(O2,c2,v2),···,Bn=(On,cn,vn)的“单向与相关”的相关型知识的一般表达式为

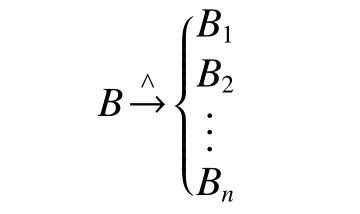
4）多个基元B1=(O1,c1,v1),B2=(O2,c2,v2),···，Bn=(On,cn,vn)与 一个基元B=(O,c,v)的“单向与相关”的相关型知识的一般表达式为

1.2 可拓知识表示

可拓数据挖掘的目的是获取基于可拓变换的知识，包括基于数据库的可拓分类知识、变换的传导知识、可拓聚类知识以及基于知识库的其他有关变换的知识，简称可拓知识[23]。本文旨在研究对科学效应的知识表示，即对已有的知识进行形式化表示研究，属于变换的传导知识和基于知识库的可拓知识。可拓知识的基础是拓展型知识，本节重点介绍本文研究所使用的基于相关型知识的可拓知识表示。

基于相关型知识的可拓知识是一种传导知识，是在相关型知识的基础上，对相关规则的前件实施某主动可拓变换时，其后件就会发生传导变换，变换后获得的传导规则知识。由于相关型知识包含很多类型，根据不同类型的相关型知识，依据发散规则实施不同的主动变换，根据可拓变换的蕴含规则和传导变换规则，相应的传导变换也不相同，因此可拓知识的表示方法也不相同。

1）基于两个基元间的单向相关型知识的可拓知识表示

同理，对于多个两两相关的基元形成的相关链（网）型知识的某一前件基元实施主动变换，会获得相关链（网）型知识的可拓知识链（网）[23]，此不详述。

2）基于多个基元与一个基元的“单向与相关”型知识的可拓知识表示

同理，对于一个基元与多个基元的“与相关”、多个基元与多个基元的“与相关”的可拓知识，也有类似的表示方法，此不赘述。

3）基于多个基元与一个基元的“单向或相关”型知识的可拓知识表示

同理，对于一个基元与多个基元的“或相关”，多个基元与多个基元的“或相关”的可拓知识表示，也有类似的表示方法，此不赘述。

1.3 科学效应

科学效应是各领域定律，它描述在科学原理和系统属性控制下输入与输出的转换关系，以实现相应的功能，包括几何效应、物理效应、化学效应和生物效应等[24]。在不同的理论体系，对科学效应输入与输出有着不同形式的表达。发明问题解决理论（theory of the solution of inventive problems，TRIZ）中认为，输入与输出形成效应；统一结构创新思维（unified structured inventive thinking，USIT）中认为，输入与输出经过转换形成效应；统一的TRIZ（Unified-TRIZ,U-TRIZ）中认为，两个属性相互作用形成效应[25]。上述对科学效应的这些研究，都没有形式化定量化地表述效应中输入与输出间的相关关系，也没有详细说明输入与输出之间的转换机理与转换过程，也没有提出利于计算机表示科学效应的知识表示模型。本文中研究的部分几何效应的输入与输出的关系，如表1 所示。

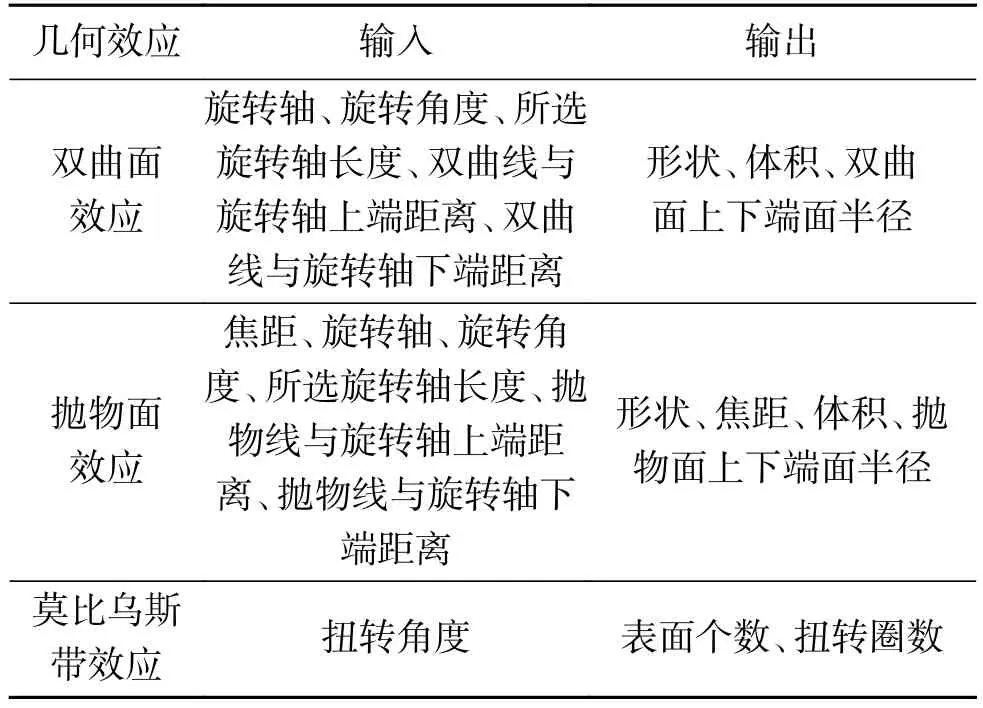
表1 部分几何效应表达Table 1 Expression of partial geometric effect

2 几何效应的可拓知识表示方法

在TRIZ 中，科学效应主要面向功能问题求解，是对系统输入输出间转换过程的描述，它是一种变化的知识，一个效应可以有多个输入、输出或控制流，即一个效应可能实现多个功能，一个问题的解也可能对应多个科学效应。目前对科学效应知识表示的研究，大都基于功能到效应的映射的知识表达，并没有详细地形式化表达出输入与输出之间的转换关系。而从可拓学的角度看，输入与输出之间是相关的，存在一定的函数关系，即具有相关关系的基元之间，若一个基元发生主动变换将导致另一个基元发生传导变换。本文运用可拓知识表示方法表示几何效应中输入与输出的变换关系，形成几何效应的可拓知识。几何效应的可拓知识表示方法流程如图1 所示。

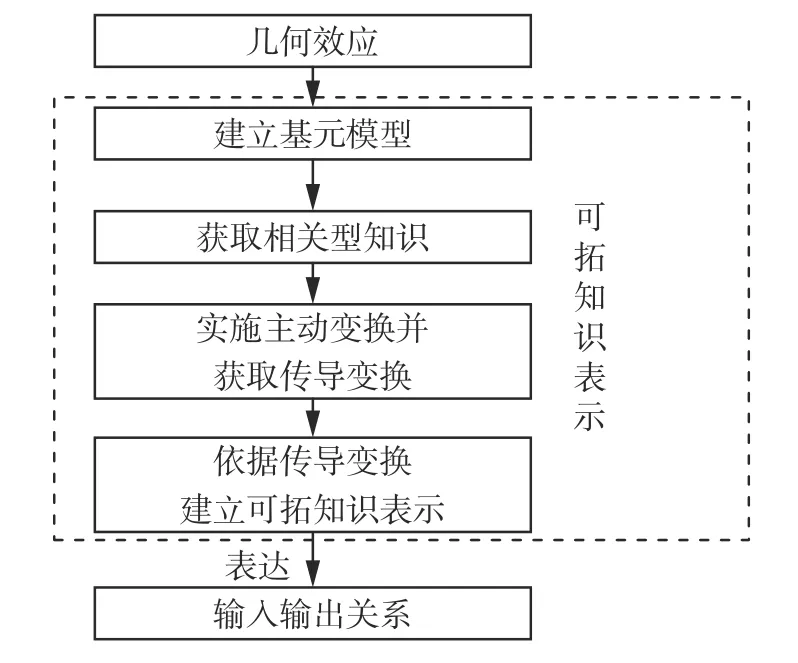
图1 几何效应的可拓知识表示方法流程Fig.1 Process of extension knowledge representation of geometric effects

具体步骤如下：

1）根据几何效应内容和工程技术领域应用需求，建立输入几何对象、输出几何对象的基元模型；

2）根据领域知识和基元的相关规则，建立基元间的相关关系，形成相关链（网）；

3）根据主动变换、传导变换知识和基元的发散规则，对相关网中某基元实施主动变换，再根据可拓变换蕴含系和传导变换规则，会得到一系列的传导变换，进而建立可拓知识表达式，实现输入与输出的转换关系的知识表示。

2.1 双曲面效应的可拓知识表示

双曲面效应是指双曲线绕某条选定的直线或其对称轴（作为旋转轴）旋转而生成的曲面[25]。在实际应用双曲线生成双曲面时，一般步骤是：首先根据实际问题的要求选取双曲线的类型，然后选择该双曲线的一侧图形，确定对应于要使用的旋转轴的长度及双曲线与旋转轴的最小距离和最大距离，再选定某条直线作为旋转轴并设定旋转角度进行旋转，生成所需的双曲面。

当工程技术领域应用该效应研制相应的产品时，一般是应用该效应产生解决技术领域相应问题的技术特征和相应的符合要求的范围。以图2 的右侧图形为例，介绍双曲面效应的可拓知识表示。

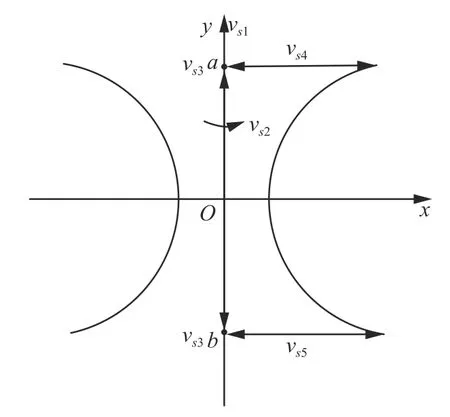
图2 双曲线Fig.2 Hyperbola

设Os为图2 中双曲线的右侧图形，选定某条直线vs1作为生成双曲面的旋转轴cs1，旋转角度cs2的量值为vs2，所使用的旋转轴的两个端点坐标cs3的量值为图2 中没有：vs3，所使用的双曲线与旋转轴上端的距离cs4和下端距离cs5的量值分别为vs4和vs5。设Od为由双曲线Os绕其对称轴y轴旋转而成的双曲面，建立物元模型:

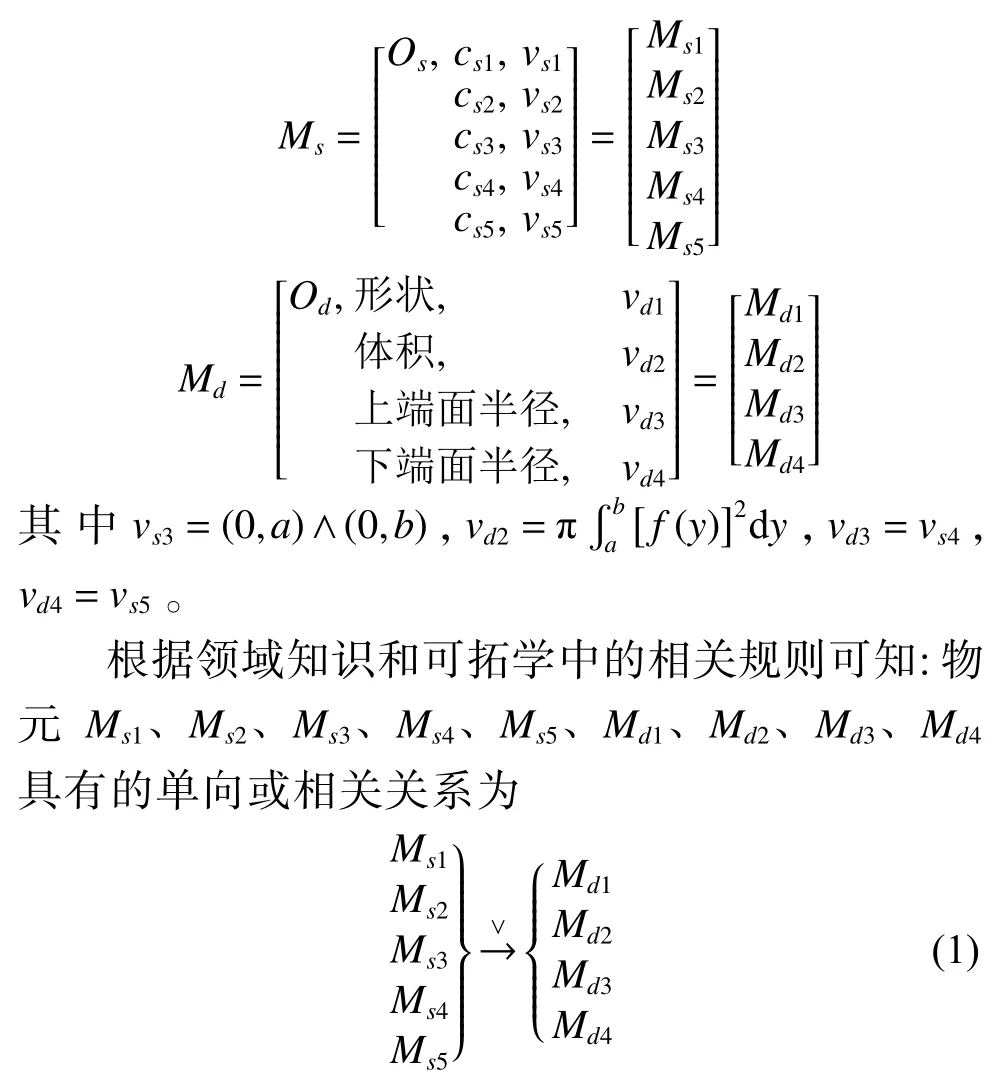
再根据主动变换、发散规则、相关关系式（1）及传导变换可知，若实施主动变换

说明：以上双曲面效应的可拓知识表示，是在不考虑领域应用的情况下的通用可拓知识，当在实际领域中应用该可拓知识时，还需要考虑该可拓知识的输出与领域问题的相关性，并在此可拓知识的基础上进一步拓展，获得面向领域应用的领域可拓知识。

2.2 抛物面效应的可拓知识表示

抛物面效应是指抛物线绕对称轴旋转所得到的曲面[25]。以图3 所示的抛物面为例，介绍抛物面效应的可拓知识表示。

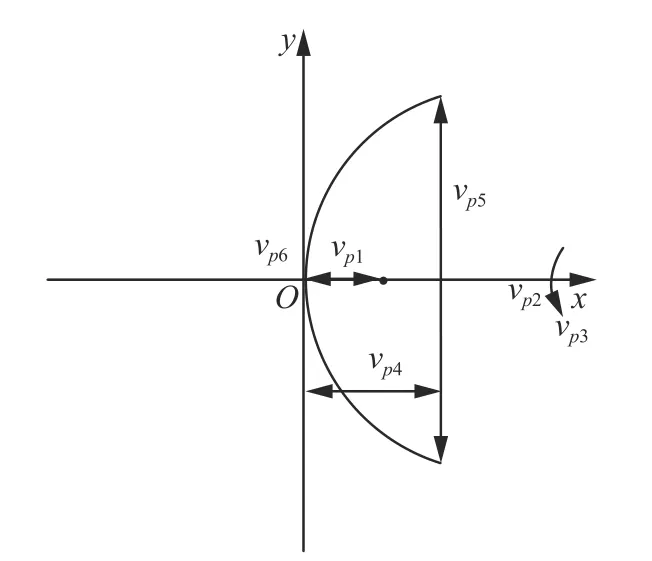
图3 抛物线Fig.3 Parabola

设Op为抛物线，其焦距cp1的量值为vp1，其对称轴vp2作为生成抛物面的旋转轴cp2，旋转角度cp3的量值为vp3，所使用的旋转轴的长度cp4的量值为vp4，所使用抛物线与旋转轴上端的距离cp5和下端距离cp6的量值分别为vp5和vp6。设Ot为抛物线Op绕其对称轴x轴旋转而成的椭圆抛物面，建立物元模型：

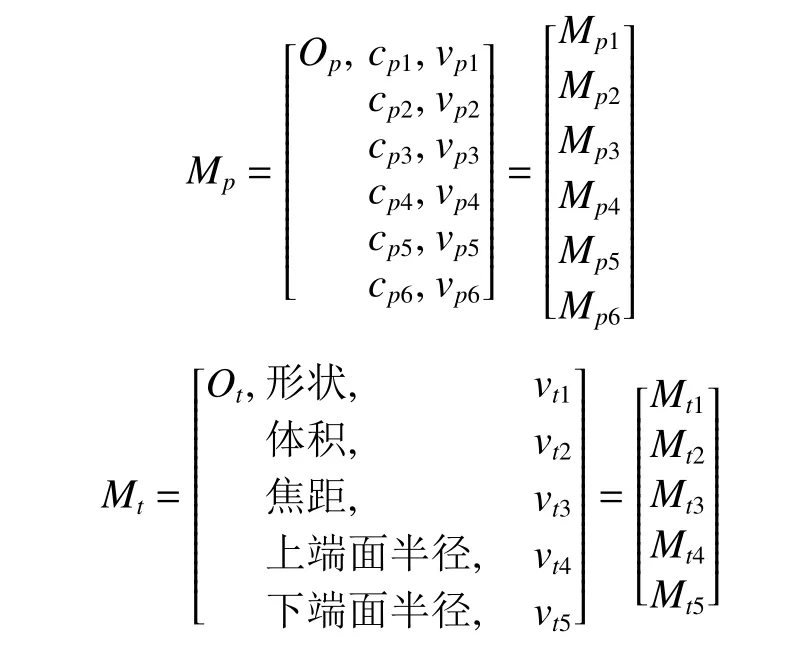
根据领域知识和可拓学中的相关规则可知：物元Mp1、Mp2、Mp3、Mp4、Mp5、Mp6、Mt1、Mt2、Mt3、Mt4、Mt5具有单向或相关关系：

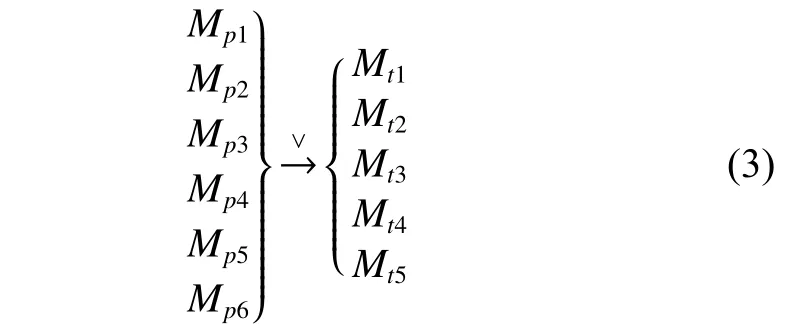
再根据主动变换、发散规则、相关关系式（3）及传导变换可知，若实施主动变换

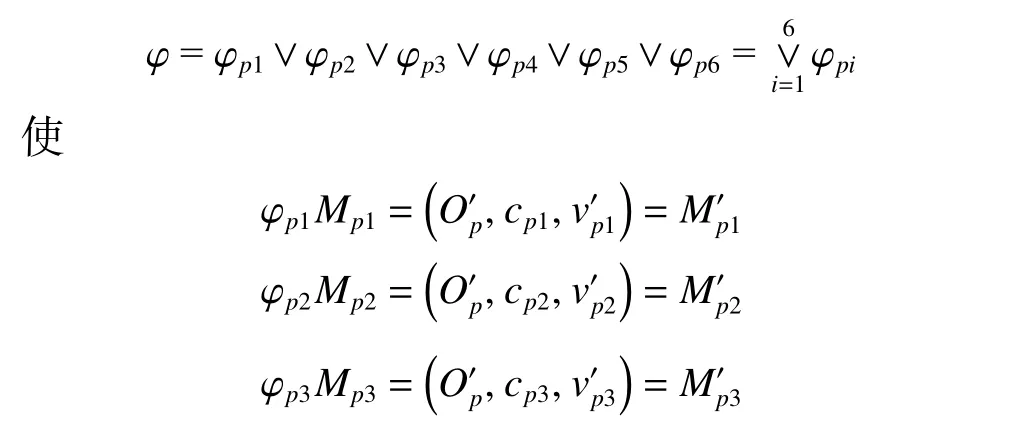
2.3 莫比乌斯带效应的可拓知识表示

莫比乌斯带效应是指将一条带的一端扭转180°，然后两端粘起来组成的只有一个表面和一个边界的带圈[25]，如图4 所示。

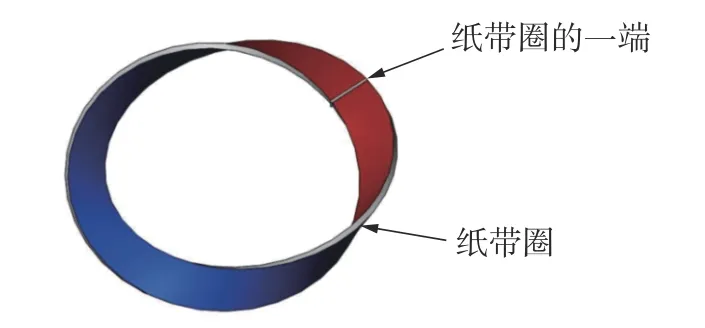
图4 莫比乌斯带Fig.4 Mobius belt

设Oz为某纸带的一端，Oq为由该纸带的两端粘起来组成的纸带圈，建立物元模型：

根据领域知识和可拓学中的相关规则可知：物元Mz、Mq具有单向与相关关系，即

再根据主动变换、发散规则、相关关系式（5）及传导变换可知，若实施主动变换 φz，使

其中n=1,3,···,2n-1。则莫比乌斯带效应的可拓知识表示为

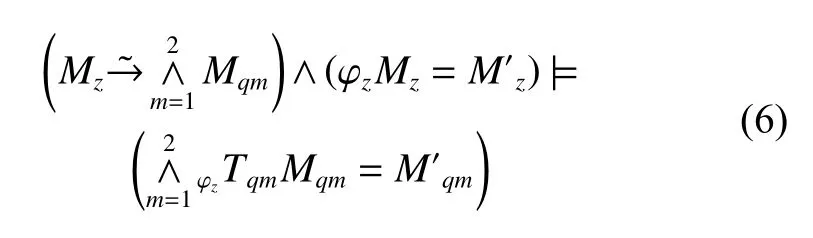
3 实例分析

城市污水处理工艺中，搅拌是关键工序之一，而搅拌器则是搅拌工艺中最重要的设备。目前主要有桨叶式、推进器式和双曲面式3 类。其中双曲面搅拌器是一种新型的搅拌器，它的叶轮体上表面是由双曲线xy=c绕叶轮体轴线旋转形成的双曲面，适用于污水处理中的厌氧池、缺氧池和选择池[26]。

某污水处理厂的正方形污水处理池，边长为9 m，水深为6 m。现有的双曲面搅拌器是由图5所示的双曲线xy=0.225绕y轴旋转360°而形成的双曲面，其叶轮半径为0.75 m，搅拌体积为216 m3。在目前的污水池中该双曲面搅拌器搅拌范围较小，可能会导致局部流速低、混合不充分以及搅拌池底有污泥沉积的现象。

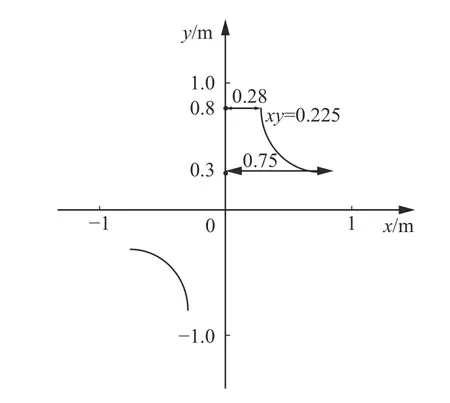
图5 双曲线Fig.5 Hyperbola

对上述的问题进行分析，发现需要通过增大搅拌器的体积来增大搅拌范围，再通过查询科学效应率，最终采用双面效应来实现。根据2.1 节的双曲面效应的可拓知识可知，选择不同的双曲线Os，可以获得不同形状和体积的双曲面Od。

为了将搅拌池内的污水充分混合均匀，就需要将该问题中搅拌器的搅拌体积增大到486 m3。

设与初始的双曲线、双曲面和双曲面搅拌机的物元模型对应的一般物元模型为

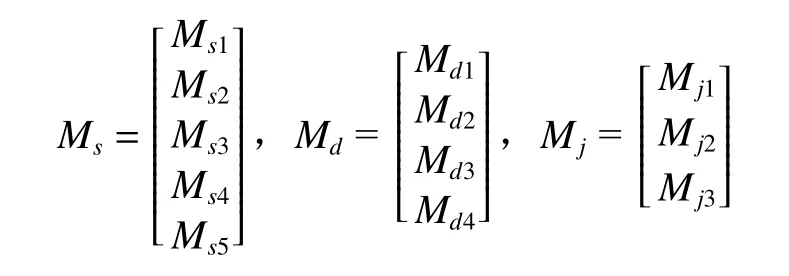
再根据双曲面效应的相关关系式（1），在旋转轴和旋转角度的量值不需要改变的情况下，结合实例应用的领域知识，以相关关系式（1）为基础，进一步分析得到结合领域应用的相关关系为

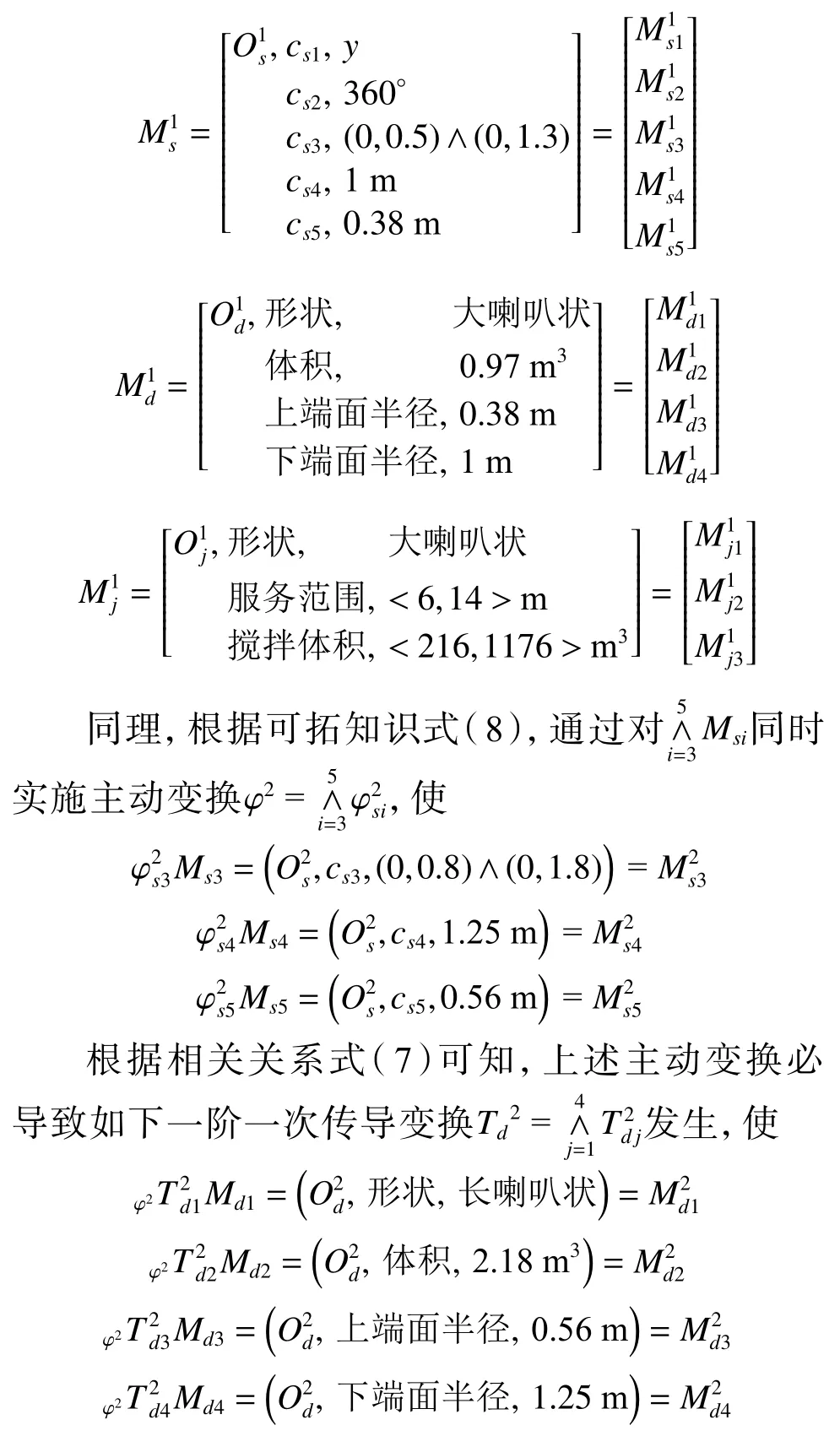
再根据相关关系式（7）可知，必导致一阶二次传导变换同时发生，使

经上述可拓变换，得到双曲面的下端面半径为1m 的双曲面搅拌器，其物元模型为

再根据相关关系式（7）可知，必导致一阶二次传导变换同时发生，使

经上述可拓变换，得到双曲面的下端面半径为1.25m 的双曲面搅拌器，其物元模型为

对上述的两种双曲面搅拌器仿真分析可得，选取叶轮半径vd4为1 m 的双曲面搅拌器能获得更佳的搅拌效果，还能有效防止污水池底部污泥的沉积。因此，利用可拓知识式（8），改良了原有的双曲面搅拌叶轮，通过改变双曲面搅拌机的母线双曲线，改变了双曲面的形状和体积，从而提高了双曲面型搅拌机的服务范围和搅拌体积。经过改良后的叶轮能够搅拌得更均匀，其结构如图6所示。

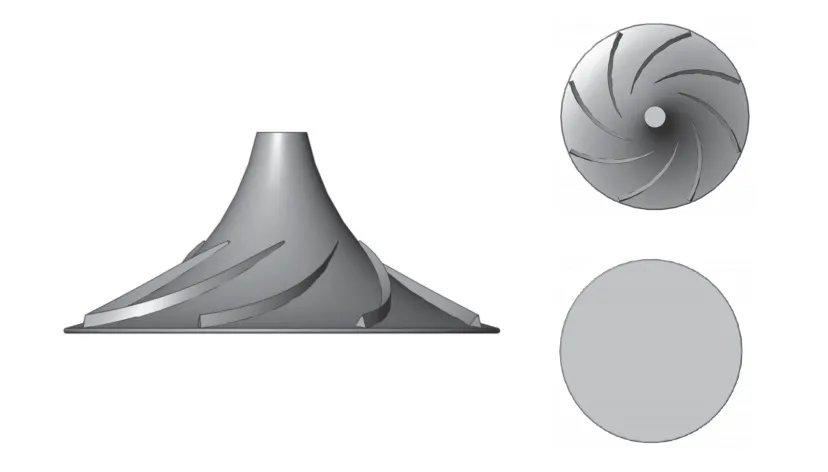
图6 双曲面搅拌机的叶轮及府视图Fig.6 Impeller and top view of hyperboloid mixer

4 结束语

科学效应对于解决产品创新、技术创新中的矛盾问题具有非常重要的作用。可拓学中的基元是形式化、定量化描述事物及其关系的基本元，可拓变换则是形式化解决矛盾问题的重要工具，可拓知识是基于可拓变换的知识。本文针对科学效应中的几何效应，结合可拓学中的发散规则、相关规则、可拓变换的蕴含规则、传导规则以及相关型知识，提出了一种面向实际应用的通用可拓知识表示方法，利用该方法能对实际应用中几何效应的输入与输出关系中所蕴含的可拓知识进行形式化表示，并通过双曲面搅拌器设计案例，介绍了结合领域知识进一步拓展相应的可拓知识以解决领域问题的方法，验证了该方法的可行性。对科学效应的可拓知识表示研究，可以使设计人员更加全面地理解几何效应实现的机理，为工程技术领域相关矛盾问题的求解提供知识依据，以便更准确地选择应用几何效应解决实际问题，也为其他类型科学效应如物理效应、化学效应和生物效应等的可拓知识表示研究打下良好基础，并可为进一步建立面向可拓智能设计的可拓知识库系统提供一种参考依据和可操作方法。