基于灵敏度聚类的含DG配电网电压分区控制方法

郭 沛，王利利，李 锰，陈 春

(1.国网河南省电力公司，河南 郑州 450000；2.国网河南省电力公司三门峡供电公司，河南 三门峡 472000；3.国网河南省电力公司经济技术研究院，河南 郑州 450052；4.长沙理工大学电气与信息工程学院，湖南 长沙 410114)

2020年习近平主席多次在国际会议上提到碳达峰、碳中和，提出力争2030年前二氧化碳排放达到峰值，努力争取2060年前实现碳中和。2021年3月1日，国家电网有限公司发布了“碳达峰、碳中和”行动方案，其中特别强调加强电力技术创新，大力发展清洁能源，最大限度开发利用风电、太阳能发电等新能源，坚持集中开发与分布式并举。

在此低碳化、去碳化的能源转型期，配电系统面临高渗透率可再生能源技术挑战。高渗透率分布式电源的接入，改变了传统配电网作为单一受端网络的特性，增加了配电网运行方式的灵活性[1-3]，但同时也带来配电网电压波动甚至越限问题，若配置不当还可能增加系统网络损耗，给配电网的运行安全带来隐患[4-6]。

目前针对含分布式电源(distributed generation，DG)的配电网电压控制已有相关研究。文献[7]充分考虑分布式电源的无功调节能力，结合节点电压灵敏度计算进行电压控制；文献[8]通过计算灵敏度考虑各种电压控制方法的相互影响，能有效降低网损；文献[9]基于模型预测，利用有载调压变压器调节系统电压，但目前有载调压变压器的调节能力较差，需考虑与分布式电源配合控制；文献[10]通过计算最优加权值来确定分布式电源的控制策略，对电压波动进行实时优化，但优化的经济性无法保证。

对于含DG配电网的电压控制方法研究很多采用分布式分区控制方法。文献[11]将配电网电压分为3种状态，对配电网电压进行分区协调控制；文献[12]以各节点间电气距离为依据进行聚类，实现配电网的电压分区控制；文献[13]通过计算灵敏度因子对配电网进行用户分区，利用逆变器进行无功调节；文献[14]提出双层优化方法，建立配电网分区和节点选择模式。以上电压控制方法通过分布式分区的方法进行配电网电压调节，但计算复杂度较高，不能针对电压薄弱点进行针对性的电压优化，导致电压调控效果不显著。

针对以上电压控制方法的不足，以提升配电系统电压水平为控制目标，提出基于灵敏度聚类的含DG配电网电压分区控制方法，首先通过潮流计算得到雅可比矩阵，然后计算各节点电压对DG出力的灵敏度，得到DG无功电压控制空间矩阵，再通过K-means算法进行聚类得到DG自适应分区，最后根据灵敏度和分区结果调节DG和无功设备出力进行电压调控。以IEEE 33节点系统作为仿真算例进行验证，该方法能有效提升系统电压水平，提高电能质量。

1 含分布式电源的配电网电压控制数学模型

配电网中电阻与电抗的比值较大，系统的有功和无功功率都很大程度地影响着系统节点电压与网络损耗。传统的电压控制方法无法满足当前配电网的可靠性要求，需要建立新的系统模型来进行电压控制。

基于灵敏度聚类分析的含分布式电源配电网电压控制方法，以提升配电系统电压水平为优化目标，考虑系统节点电压、网络功率平衡以及线路功率传输约束。

节点电压偏差最小数学描述如下：

(1)

式中n为配电网节点数量；δvq为电压偏差指标；Vi为第i个节点电压；Vei为第i个节点的额定电压。

优化的约束条件有节点电压、网络功率平衡、线路功率传输约束，分别为

Ui,min≤Ui≤Ui,max

(2)

(3)

Sij,min≤Sij≤Sij,max

(4)

式(2)～(4)中Ui为节点i的实际电压；Ui，max、Ui，min分别为节点允许的电压最大、最小值。PGi、PLi分别为与节点i相连的DG、负荷的有功功率；QGi、QLi分别为与节点i相连的DG、负荷的无功功率；N为节点数目；Ui、Uj分别为节点i、j的电压；θi、θj分别为节点i、j的相角；Gij、Bij分别为节点i与j间导纳的实部、虚部。Sij、Sij,min、Sij,max分别为节点i和j间线路传输功率及其幅值。

2 基于灵敏度聚类的分布式电源分区方法

2.1 节点电压的灵敏度计算

配电网电压水平受多种因素共同影响，任意节点的电压变化都是受系统中各节点的功率变化总和影响的[15-16]，需要计算各节点灵敏度值，选择电压薄弱点作为观测点，通过改变分布式电源出力提升系统电压水平，提高供电可靠性[17]。含分布式电源的配电网如图1所示。

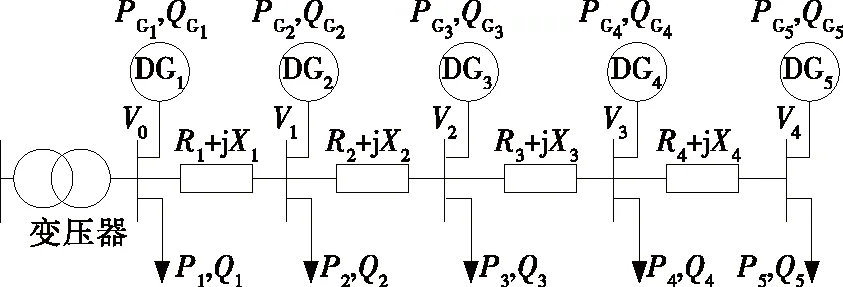
图1 含分布式电源的配电网Figure 1 Schematic diagram of distribution network with distributed generation

对于任意节点m，其节点电压为

(5)

式中Gf为节点0与m间的关联拓扑；I0m、X0m、R0m分别为电流、电抗、电阻；Ploss、Qloss分别为有功、无功功率损耗。

接入分布式电源后节点m的电压为

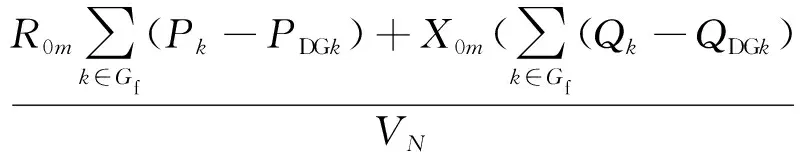
(6)

因此，在一定程度上增加分布式电源出力能有效提升系统节点电压水平。若系统有M个分布式电源，通过调节M个分布式电源的出力就能对节点m进行电压控制，节点m处的电压改变量ΔVm对M个分布式电源的有功、无功出力的改变量(ΔP，ΔQ)为

(7)

式中SP、SQ分别为节点电压Vm对于接入分布式电源的有功、无功出力的灵敏度。

通过改变分布式电源的有功、无功出力就可以进行电压控制；计算节点电压变量对分布式电源有功、无功出力的灵敏度，根据灵敏度确定分布式电源和无功设备的注入顺序。

根据式(6)，假定调节分布式电源出力时负荷功率不变，则节点m的电压Vm与接入分布式电源PDGk、QDGk的关系为

Vm=f(PDG1,PDG2,…,PDGN,QDG1,QDG2,…,QDGN)

(8)

改变分布式电源功率后节点m的电压改变量为

(9)

对于含有N个节点的系统，矩阵形式为

(10)

简化为

(11)

式中SP、SQ分别为节点电压V对于接入分布式电源的有功、无功出力的灵敏度。

通过潮流计算得到雅可比矩阵，从而计算系统节点电压对于分布式电源有功、无功出力的灵敏度，过程如下：

(12)

令

(13)

因为

(14)

所以

(15)

令

(16)

根据以上推导可得，系统节点电压Vm对于分布式电源有功、无功出力的灵敏度为

(17)

2.2 分布式电源分区方法

在配电网中，假设系统内部可控制电压的节点数目为n，分布式电源数目为w，求解某一分布式电源j注入的无功功率对n个节点电压控制的灵敏度，可以得出：

i=1,2,…，n

(18)

不断重复以上步骤，求解w个分布式电源注入的无功对各个节点的电压灵敏度，可以得到系统中 所有分布式电源无功电压控制的空间矩阵[18]：

(19)

满足分布式电源无功控制范围分区的有效性包含准则：①确保分区内的分布式电源能控制其余分区中的节点，需要分布式电源分区内的相关节点能与分布式电源有很强的耦合性；②为确保分布式电源自身的电压控制能力，需要合理控制分区的范围，还要保证分区内的节点处于互相连通的状态。

聚类分析法是处理分析数据并进行分类的重要方法，聚类分析可以将数据根据相似性或者其他标准进行分类。首先将分布式电源的无功电压控制空间矩阵进行处理，取出矩阵中灵敏度最大的元素，并将矩阵中某个元素除以最大元素Smax，得到新的元素记为Xij=Sij/Smax；然后对原矩阵中的每一元素均进行数学处理，可以得到处理后的新矩阵为

利用K-means算法计算新矩阵中的元素，将获得的数据分为3种不同类型。

K-means算法包括：①随机选取聚类中心或者借助直方图来完成选取；②将数据中心移到其所在类别的中心；③根据最邻近规则将数据点重新聚到聚类中心；④更新聚类中心，不断重复上述过程直到评价标准不再变化。评价标准为

(20)

式中J(·)为评价聚类中心的评价函数。

根据计算的灵敏度和分区结果，参考文献[17]中方法，调节电容器组和分布式电源出力，提高系统节点电压水平，整体思路如图2所示。

图2 基于灵敏度聚类的电压分区控制流程Figure 2 Voltage partition control flow chart based on sensitivity cluster analysis

3 算例仿真

采用IEEE 33节点系统作为仿真算例，如图3所示，母线电压为12.66 kV，系统总负荷为3 802.2+j2 694.6 kV·A。Vci、Vr、Vco分别取3、14、25 m/s，此处假设风机功率因数恒定，取pf=0.9，吸收和发出的有功功率为

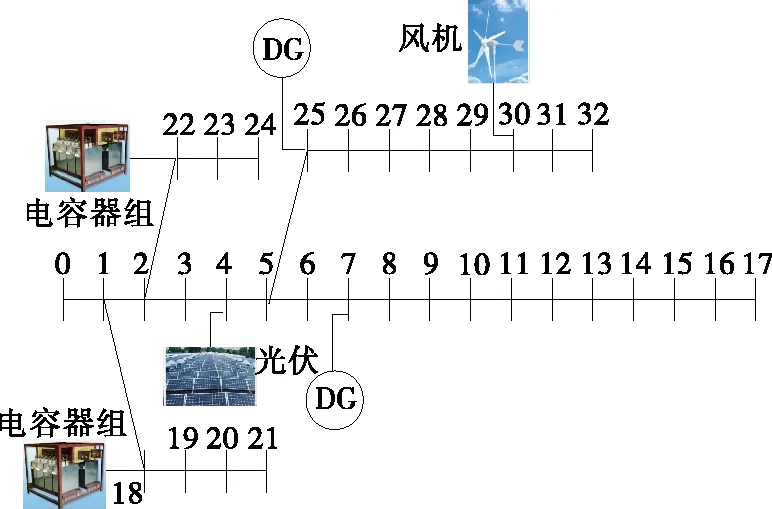
图3 33节点配电系统接线Figure 3 33-node power distribution system wiring diagram

(21)

Qw=Pw·tan(arccospf)

(22)

分布式电源、无功补偿电容器的安装位置与容量分别如表1、2所示。

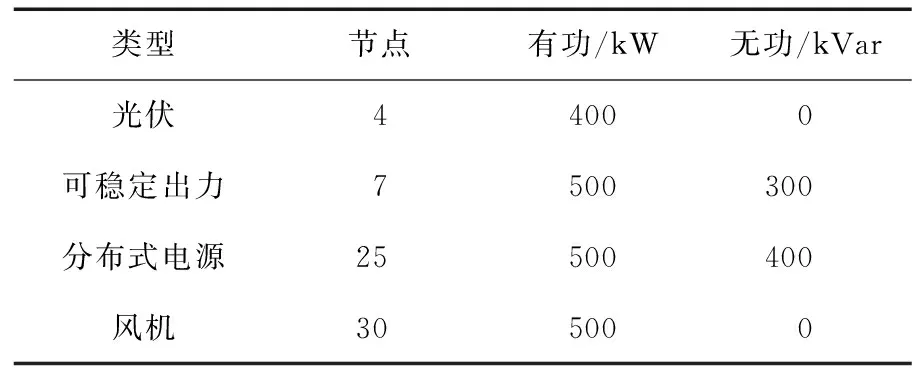
表1 DG安装位置与容量Table 1 Installation position and capacity of DG

表2 无功补偿电容器的安装位置与容量Table 2 Installation position and capacity of reactive power compensation capacitor

3.1 本文方法验证

首先计算系统潮流，投入DG前系统各节点电压分布如图4所示，通过牛拉法计算雅克比矩阵；然后计算有功和无功灵敏度矩阵，得到有功和无功出力对各节点的灵敏度情况，如图5所示。

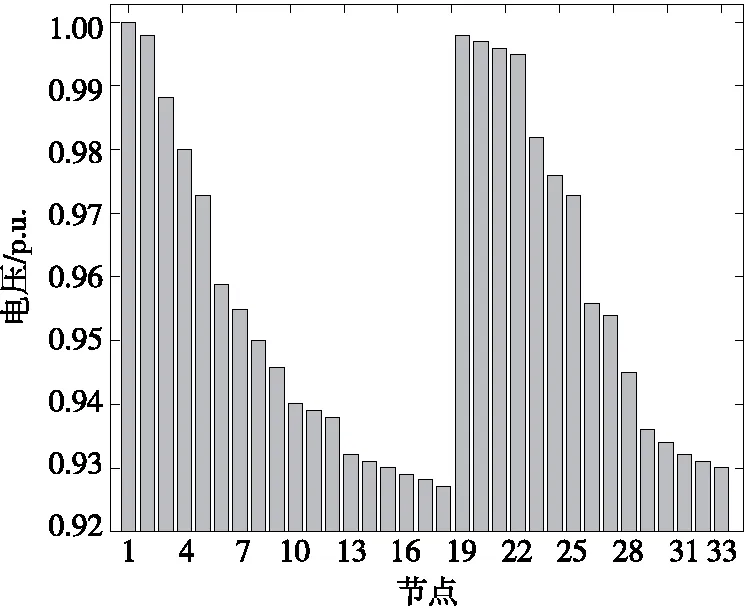
图4 投入DG前系统各节点电压分布情况Figure 4 Voltage distribution of each node in the system before DG input

图5 各节点灵敏度Figure 5 Sensitivity of each node

利用式(21)、(22)，将各节点灵敏度进行数据处理后可得

S=[6.014 2 14.563 6 7.894 6 21.391 2

14.883 7 22.388 4]

根据K-means算法，取聚类数k=3，即分为3个子类，得到的聚类结果为

子类1：6.014 20 7.894 60

子类2：14.565 3 14.883 7

子类3：21.391 2 22.388 4

根据聚类结果进行系统分区，如图6所示，根据计算的灵敏度以及电容器组与分布式电源的调节方法，得出投入节点12、25的DG出力，如图7所示，投入后系统节点电压水平满足要求。

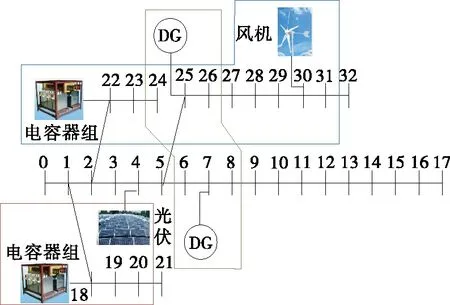
图6 分区结果Figure 6 Partition result diagram

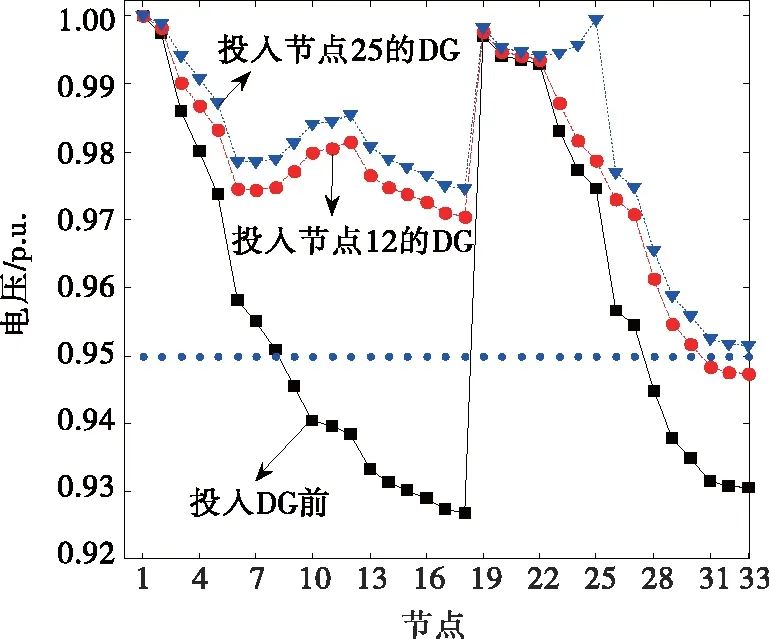
图7 投入DG后系统各节点电压分布情况Figure 7 Voltage distribution of each node in the system after DG input

投入节点12后DG系统依然存在节点31、32、33的电压不满足要求，但继续投入节点25后，系统的所有节点均满足要求。

3.2 本文方法与2种智能算法对比

将本文方法与和声、遗传算法进行对比，其中和声算法参数：和声记忆库的大小(HMS)取为10，记忆库的考虑概率(HMCR)为0.85，扰动概率(PAR)为0.3；遗传算法参数：种群数目(POP)为30，交叉概率(CP)为0.85，变异概率(MP)为0.05。

利用和声算法进行配电网电压调控，协调系统中分布式电源出力，通过选择随机数不断产生新解并不断更新最差解，直到系统节点电压均在合理范围内；利用遗传算法以电压偏差最小为目标进行电压调控，随机生成新个体，通过种群的交叉和变异不断优化，达到调控系统电压的效果；而本文方法通过聚类分析，不断更新聚类中心，得到各分布式电源的自适应分区结果，结合灵敏度计算实现系统的电压控制，相比于其他2种智能算法，本文方法利用灵敏度计算刻画系统电压薄弱点，通过聚类得到分布式电源分区，实现系统电压的分区控制。

3种方法投入分布式电源后各节点电压分布情况对比如图8所示，通过本文方法进行电压调控后系统各节点电压水平明显优于其他2种智能算法。

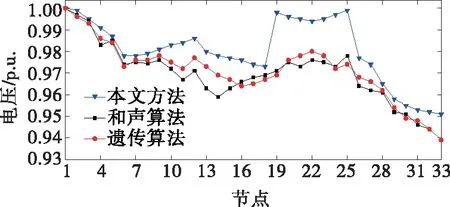
图8 3种方法投入DG后各节点电压分布情况对比Figure 8 Comparison of voltage distribution of each node after DG input by three methods

通过与和声、遗传算法对比，2种智能算法的求解过程需要不断搜索，计算时间较长，分别为2.19、3.47 s，而本文电压控制方法通过灵敏度计算和聚类分析，对分布式电源进行自适应分区，计算时间仅为0.62 s，且电压控制后能有效提升系统各节点电压水平，验证了本文方法的优越性。

4 结语

本文提出基于灵敏度聚类的含DG配电网电压分区控制方法。①通过计算分布式电源出力对所有节点电压的灵敏度，能直观地刻画出系统电压薄弱点，得到分布式电源有功和无功出力对于系统节点电压变化的影响程度；②根据灵敏度矩阵得出分布式电源的无功电压控制空间矩阵，再通过K-means算法进行聚类，得到分布式电源的分区情况，实现系统中分布式电源的分区调节；③根据灵敏度和分区结果调节分布式电源和无功设备出力，能针对电压薄弱点进行定向补偿，有效提高系统电压水平。通过33节点算例进行验证，经过本文电压控制方法，系统各节点电压均得到提升且满足要求，且与2种智能方法对比具有较明显优势，能有效提升系统电压水平，验证了本文方法的合理性与优越性。