基于MPA-SVM的煤矿抛掷爆破爆堆形态预测❋
2023-01-13王昱琛杨仕教郭钦鹏
王昱琛 杨仕教 郭钦鹏 尹 裕②
①南华大学资源环境与安全工程学院(湖南衡阳,421000)
②中钢集团马鞍山矿山研究总院股份有限公司(安徽马鞍山,243000)
引言
露天煤矿主要利用抛掷爆破拉斗铲倒堆工艺进行开采,抛掷爆破后的堆形(爆堆形态)是分析爆破效果的关键指标[1]。一方面,通过抛掷爆破技术将剥离岩土直接抛入采空区,减少二次剥离倒堆量,大幅度降低煤矿开采成本,提高拉斗铲倒堆工艺效率[2];另一方面,爆堆形态反映爆破设计参数是否合理[3-4],直接影响煤矿拉斗铲倒堆工艺流程的成本和效率,也为爆破参数优化提供必要的依据,可用于指导和优化爆破方案设计。因此,研究爆堆形态对煤矿开采具有重要的工程意义。
对爆堆形态的研究方法经历了从传统的经验分析到线性回归方程,再发展到仿真模拟及智能预测。目前,专家学者在爆堆几何形态研究中已取得一定进展。李胜林等[5]通过无人机摄影测量技术,采用Weibull概率分布曲线拟合爆堆轮廓,并与实际爆堆曲线进行对比,得到Weibull模型两个控制参数的取值范围;齐留洋等[6]建立了基于Weibull函数的爆堆形态神经网络预测模型,在巴润露天矿的现场应用结果表明,该方法相对误差小于10%,符合实际工程要求;韩亮等[7]为探究影响爆堆几何形态的主控因素,通过Weibull分布函数对爆堆参数进行量化,利用灰色关联度分析主次关系,认为适当提高炸药单耗可以获得理想的爆堆形态;李志航等[8]为提高爆堆形态的预测精度,提出了BP神经网络与Weibull模型相结合的预测方法,预测绝对误差未超过15%;刘希亮等[9]为进一步提高BP神经网络的预测准确率,利用遗传算法优化BP初始权值,显著降低了抛掷率的预测误差;温廷新等[10]引入极限学习机(ELM)对爆堆形态进行预测,并与BP进行对比,发现由ELM预测得到的结果更加接近实际爆堆形态。
但由于煤矿抛掷爆破数据的稀缺性,传统神经网络模型需要大量训练数据才能得到较为理想的预测效果,因此,在爆堆形态的预测应用中有一定的局限性。另外,针对爆堆形态的预测研究较少,仍存精度不足的问题。
鉴于此,为解决样本数量有限的问题,提高爆堆形态预测精度,采用专门研究小样本数据的支持向量机(support-vector machine,SVM)作为建模的理论基础。在前人研究的基础上,引入新型元启发式算法海洋捕食者(marine predators algorithm,MPA)优化惩罚因子C和核函数参数g,建立精度较高的MPA-SVM预测模型。将模型应用于煤矿抛掷爆破开采的研究中,通过黑岱沟工程实例的样本数据,对堆型进行预测模拟,进而通过预测结果指导爆破方案的设计。
1 MPA-SVM理论
1.1 MPA基本原理
MPA是Faramarzi等[11]于2020年在适者生存理论基础上提出的优化算法:捕食者根据猎物的位置信息搜索猎物,其中,顶级捕食者(最优解)具有更高的觅食天赋。
MPA根据捕食者和猎物的不同速度比,将优化过程分为3个阶段:
1)高速度比,即猎物移动速度快于捕食者;
2)等速度比,即捕食者和猎物速度几乎相同;
3)低速度比,即捕食者移动速度快于猎物。
针对不同阶段中运动性质的规则,对捕食者和猎物指定和分配特定的迭代周期。
1.1.1 高速度比(I阶段)
I∈(0,Imax/3),其中,I为当前迭代,Imax为最大迭代。该阶段,猎物的运动速度远高于捕食者,捕食者默认采取不移动状态,猎物采取随机移动模式搜索自己的食物。该阶段为全局搜索阶段,数学模型为
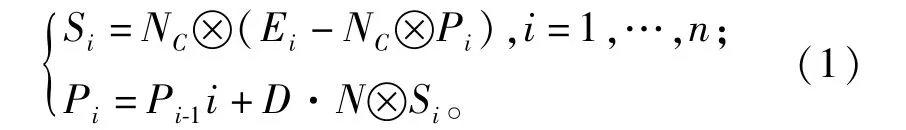
式中:Ei为捕食者种群;Pi为猎物种群;捕食者和猎物的个数均为n;Si为运动的步长;NC为服从正态分布的随机数的向量,表示布朗运动;NC与Pi的逐项相乘模拟猎物的运动;D为常数项,通常取D=0.5;N是[0,1]中的一个均匀随机数向量。
1.1.2 等速度比(II阶段)
I∈(Imax/3,2Imax/3)。该阶段,捕食者和猎物的移动速度相同,捕食者通过布朗运动搜索猎物,猎物通过莱维运动更新自身的位置。全局搜索与局部寻优并重。因此,该阶段中,种群被分为等量的两部分:一半的个体用于局部寻优;另一半被用于全局搜索。
猎物局部寻优数学模型为
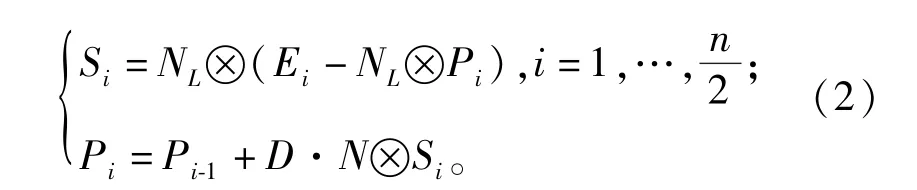
式中:NL为服从莱维分布的随机数的向量,表示莱维运动。
捕食者全局搜索数学模型为
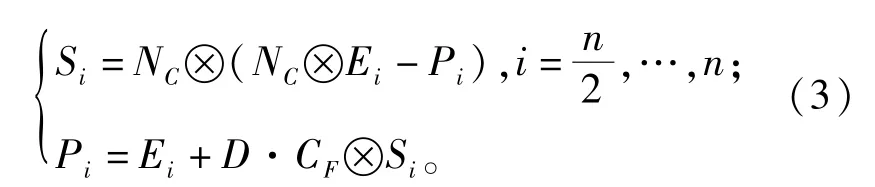
式中:CF表示步长的自适应参数,计算方式为
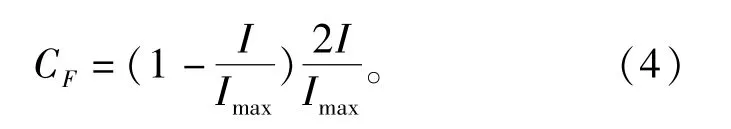
1.1.3 低速度比(III阶段)
I∈(2Imax/3,Imax)。该阶段,捕食者移动速度快于猎物,捕食者通过莱维运动搜索猎物。该阶段为局部寻优阶段,数学模型为

此外,在每次迭代结束后,MPA通过利用鱼群聚集装置效应(FADs)使捕食者进行更长的跳跃,以避免陷入局部最优。数学模型为
如果r≤FADs:

如果r>FADs:
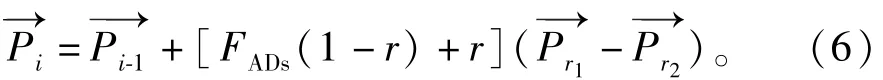
式中:FADs为影响概率,通常取0.2;为包含数组0和1的二进制向量,构造方法是在[0,1]中生成一个随机向量,如果数组小于0.2,则将数组更改为0,如果数组大于0.2,则将数组更改为1;r为[0,1]内的随机数;r1、r2分别为猎物的随机索引;和分别为猎物种群中同一维度的最小值和最大值。
1.2 MPA优化SVM算法参数
SVM[12]是近年来比较流行的一种从VC维(Vapnik-Chervonenkis dimension)概念中发展出来的机器学习算法,以结构化风险最小原理代替了传统神经网络中的经验风险,解决了小样本容量时难以克服局部极值的缺陷。
根据SVM的原理,选择不同类型的核函数参数会直接影响预测结果,惩罚因子C的大小也决定了预测效果的优劣。为了达到最优参数的目标,提出了利用MPA对C、g进行优化的方法。MPA-SVM模型流程如图1所示。

图1 MPA-SVM模型流程示意图Fig.1 Flow chart of MPA-SVM model
该方法建模步骤如下:
1)数据集预处理。将集合进行归一化操作后,划分为训练样本集和测试样本集。
2)模型初始化。设置海洋捕食者算法的最大迭代次数、种群规模数量和猎物初始位置,并测试、选取合适的损失函数,完成MPA算法的初始化。
3)计算两个种群中个体的适应度。
4)MPA优化。基于MPA算法的原理,依据当前迭代次数进行阶段的优化过程更新猎物位置。
5)应用式(5)(即FADS)更新猎物位置,依据猎物位置更新捕食者位置。
6)重新计算个体适应度,判断是否满足MPA结束条件。如果满足,输出最优化参数,更新C和g;若不满足,返回步骤3),直至符合适应度要求。
7)建立MPA-SVM模型。根据更新后的最优参数C、g建立新的MAP-SVM爆堆形态预测模型。
8)输出结果。将划分后的测试样本代入MPASVM模型进行预测和分析。
2 基于MPA-SVM的爆堆预测模型参数的选取
2.1 模型输入参数
露天煤矿抛掷爆破效果受许多不确定因素的影响,在目前的研究进展中,对于各因素与抛掷结果之间的复杂非线性关系,分3个方面进行研究[8]:岩石地质条件、爆破设计和炸药性质。
本次采用的黑岱沟露天煤矿抛掷爆破案例,工程开展区域台阶的岩石性质变化不大,因此,将岩石地质条件视为同质[4,9],不单独列为输入参数。另外,针对同一抛掷爆破工程,使用的炸药类型相同,爆破实施过程中通常不改变装药结构、填塞方法、布孔方式、起爆网路等。因此,重点通过调整炸药单耗、台阶高度、最小抵抗线、孔距、排距等设计参数优化抛掷爆破效果。
综合上述,选取以下8个参数作为预测模型的输入参数:炸药单耗Q,kg/m3;台阶高度H,m;煤层厚度Hc,m;采空区上口宽度Lk,m;最小抵抗线W,m;孔间距a,m;排间距b,m;坡面角a1,(°)。
2.2 模型输出参数
经过分析发现:一方面,由于爆破漏斗现象,在实际抛掷爆破过程中,爆堆曲线的后半段会出现下陷[6],去掉因爆破漏斗产生下陷的前半部分,曲线具有Weibull函数的分布特征;另一方面,Weibull函数在对爆堆形态进行模拟时,利用概率统计方法代替繁琐复杂的力学推导过程,操作简便性明显提高。
根据质量守恒定律,爆破前与爆破后的岩石质量相等,关系式为

式中:lm为最远抛掷距离,m;ρb和ρa分别为岩石爆破前和爆破后的岩石密度,kg/m3;h(x)为爆堆在x坐标轴上的爆堆高度,m;S0为爆破前岩石的剖面面积,m2。
将式(7)进行无量纲化,即

式(8)中,H(X)为Weibull概率密度函数,满足以下数学关系:
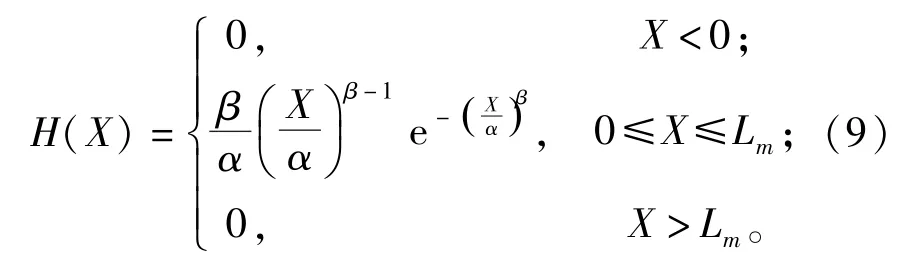
式中:α和β是控制Weibull曲线形状的关键参数,α为比例参数,β为形状参数,β>1。
如果α和β取值合适,可使得H(X)在Lm处的变化程度尽可能小。因此,式(8)可以进一步化为

将Weibull分布函数应用于对爆堆形态预测的过程中。自变量的取值范围对于真实爆堆的变化范围存在较大差距;因此,需要将真实爆堆曲线进行无量纲化处理,使得Weibull曲线与实际爆堆形态可以在同一个坐标系中进行反映。将爆堆形态曲线无量纲化后,通过改变α和β[10],即可实现对Weibull模型的调控。因此,选择松散系数ξ、控制参数α和β作为基于Weibull函数的爆堆形态预测模型的输出参数。
3 工程应用
3.1 数据样本
根据黑岱沟露天矿高台阶抛掷爆破的实际案例情况,引用文献[7-10]中的42组样本数据进行研究。其中,随机抽取10组作为测试样本,见表1。

表1 测试样本Tab.1 Test samples
设置初始化时,算法的最大迭代次数为100,种群个数为30。MPA算法中,FADs为0.2,P为0.5;PSO算法(particle swarm optimization,粒子群优化算法)中,c1和c2分别为1.9和1.4,惯性权重ω为0.9;SSA算法(sparrow search algorithm,麻雀搜索算法)中,PD为0.7,SD为0.2;设置SVM模型的核函数为径向基函数,ELM模型的隐含层个数为12,通过优化算法进一步确定最优权值和阈值。其中,惩罚因子C和核函数参数g的调整范围是:C∈
[10-2,1],g∈[2-5,25]。以均方误差RMSE作为迭代寻优过程中评价最佳适应度的标准。在建立模型前,均对数据进行归一化处理,以消除样本中数量级差异对结果的影响。最后,选取平均绝对误差RMAE、相关性系数R2和均方根误差RMSE作为性能评价的指标。
3.2 模型预测结果分析
3.2.1 优化算法对比
将PSO-SVM、SSA-SVM与MPA-SVM 3种优化算法的适应度进行对比,如图2所示。通过曲线对比可以明显看到,MPA-SVM收敛结果最小,下降速度较快。综合而言,MPA-SVM模型具备较好的寻优效率和极值搜索能力,并在快速迭代中显示出稳定性。因此,将该算法应用于SVM的C、g寻优是可靠的。

图2 3种模型适应度对比Fig.2 Comparison of adaptation curves of three models
3.2.2 预测模型对比
为了进一步测试MPA-SVM模型在煤矿开采应用中的拟合效果,验证该预测模型相较其他算法模型在煤矿爆堆形态预测方面具有一定优势,选择SVM、PSO-SVM、SSA-SVM、PSO-ELM和MPA-ELM 5种模型进行回归预测对比,针对松散系数ξ、比例参数α和形状参数β3个参数分别进行预测。预测结果如表2所示。6种模型预测相对误差对比如图3所示。

图3 相对误差对比Fig.3 Comparison of relative errors
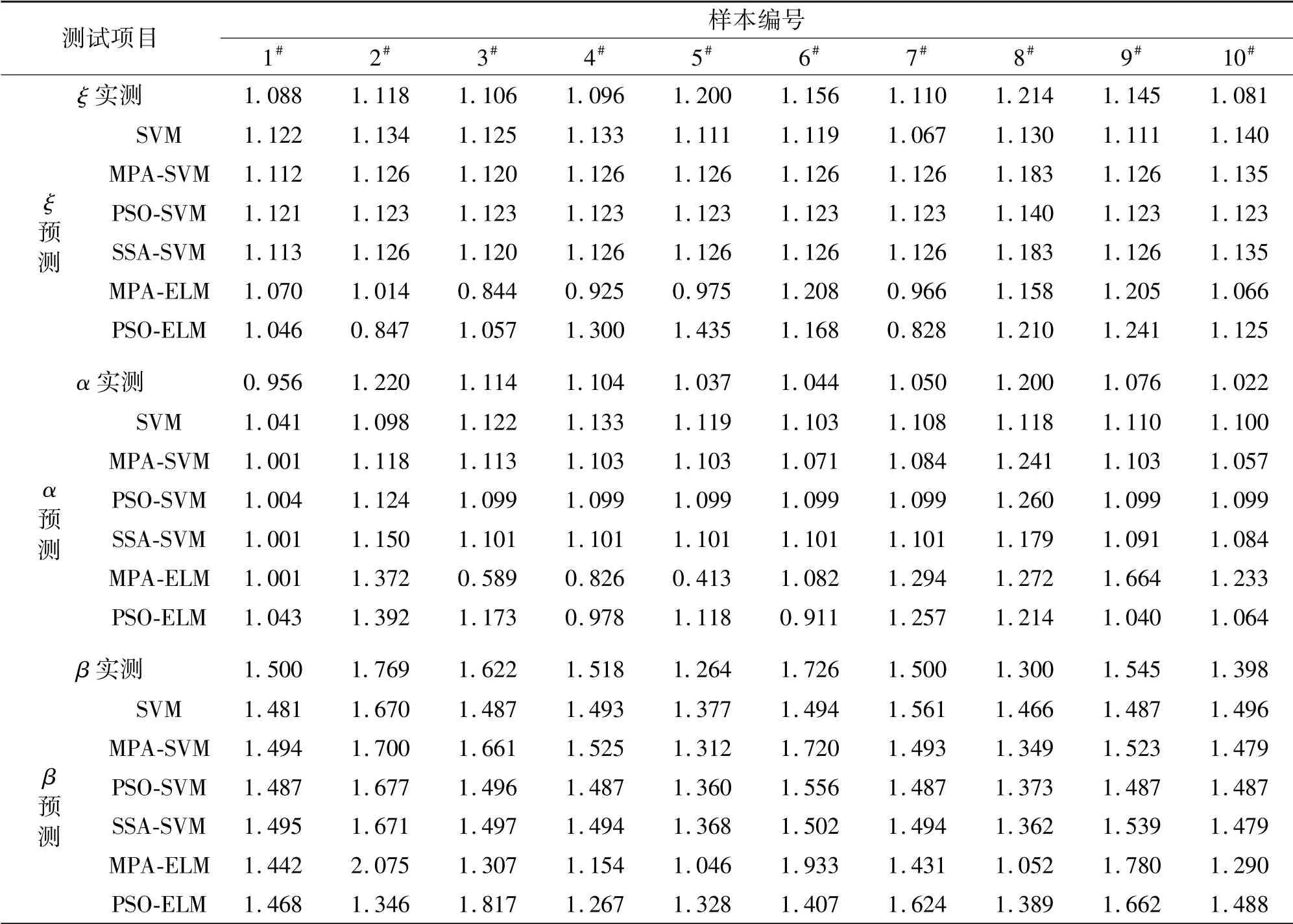
表2 各预测模型的测试结果Tab.2 Test results of each prodiction model
根据柱状对比图可知:相较于以ELM为基础的预测模型,以SVM为基础的预测模型整体预测结果相对误差更小;相较于其他5种模型,MPA-SVM对于3个参数的预测误差率都控制在5%以内,表现出较好的泛化能力。为更直接对比6种预测模型的准确性,引入RMAE、R2和RMSE评价指标进行验证,详细结果见表3。
通过表3的结果对比可知:

表3 性能指标对比Tab.3 Comparison of performance index
1)选择同一种优化函数的基础模型进行R2对比,MPA-SVM方法分别是0.955、0.978、0.946,MPA-ELM方法分别是0.863、0.680、0.621,PSOSVM方法分别是0.819、0.869、0.887,PSO-ELM方法分别是0.669、0.546、0.508。对比分析得出,以SVM为基础的模型的拟合结果较优。
2)MPA-SVM、PSO-SVM和SSA-SVM模型对ξ预测的RMSE分别为0.063、0.068和0.067,相较于基础SVM预测模型,分别降低了24%、18%和19%;预测α的RMSE为0.075、0.087和0.079,分别降低了59.1%、52.4%和56.8%;预测β的RMSE为0.116、0.117和0.138,分别降低了17.7%、17.0%和2.1%。对比可以看出,MPA对SVM的性能优化程度更好,预测结果更加准确。
为更加直观地看到MPV-SVM、PSO-SVM、SSASVM 3种优化算法之间的差异,分别选择实测样本5#和样本8#为对照,拟合Weibull分布如图4所示。可以看出,MPA-SVM预测的Weibull分布曲线相较于其他两种模型更加接近实际曲线。
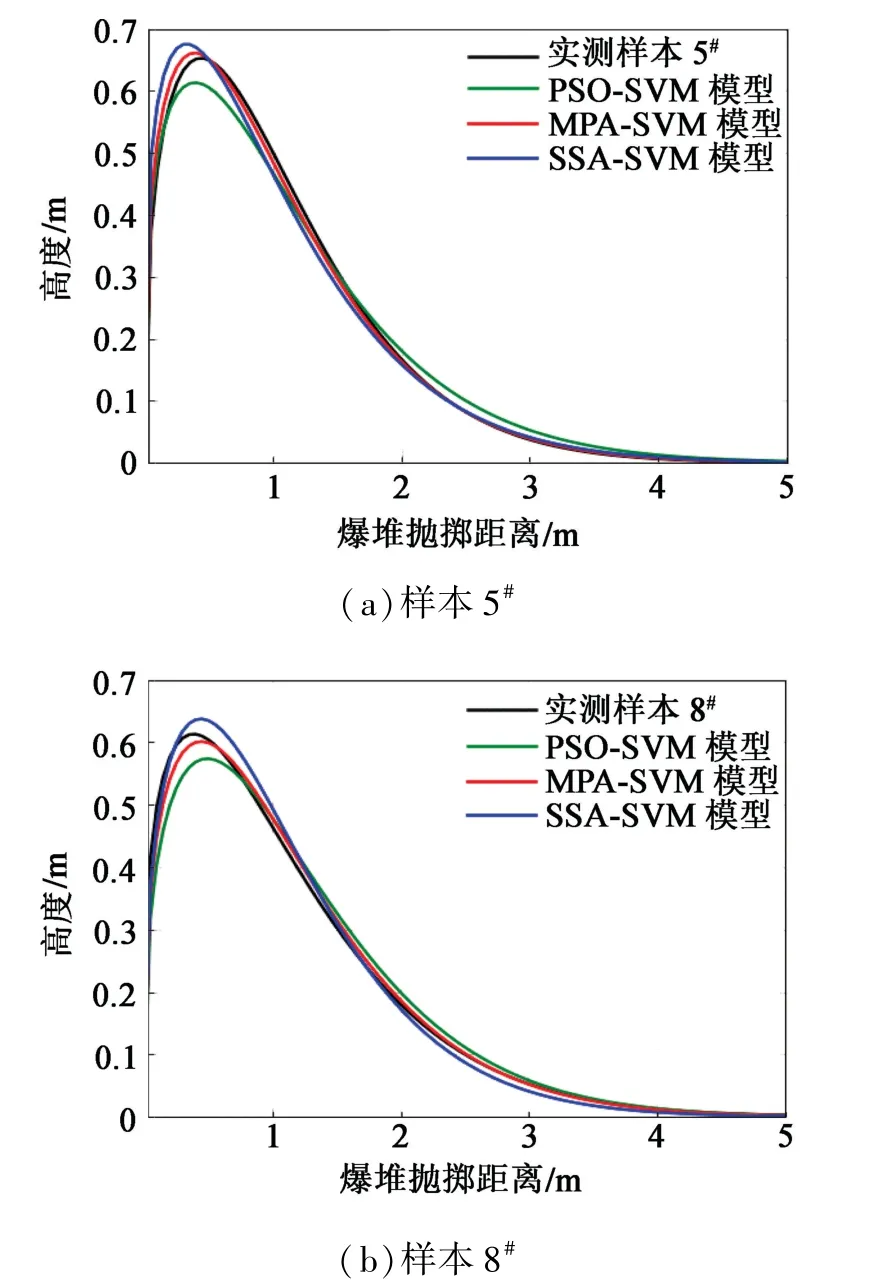
图4 预测曲线和真实Weibull曲线的对比Fig.4 Comparison of the predicted curves and the real Weibull curves
4 结论
1)采用Weibull函数模拟煤矿抛掷爆破爆堆形态,利用MPA-SVM模型,以8个设计参数为输入参数,对Weibull函数的两个控制参数和松散系数进行预测,从而实现对爆堆形态的预测,试验结果表明该方法切实可行。
2)MPA在同期条件下的迭代效率明显优于PSO和SSA算法。MPA收敛性强,具有较好的寻优精度和全局搜索能力。将MPA应用于SVM的优化
过程中,克服了常规SVM泛化能力过强、选取最优核函数参数难的问题。
3)结合黑岱沟露天矿抛掷爆破工程,MPA-SVM模型在实际应用中的相对误差控制在5%以内,预测效果明显优于其他5种模型,且拟合的Weibull曲线与实际露天矿爆堆曲线较吻合,有较好的实用价值和应用前景。
