无穷大的和与差等价代换定理及应用

田学刚，王少英

无穷大的和与差等价代换定理及应用

田学刚，王少英

（滨州学院 理学院，山东 滨州 256603）

研究自变量趋于有限值情形下无穷大的和与差等价代换问题．利用泰勒公式刻画出任意２个无穷大的和与差，当２个无穷大等价时，给出它们差的等价代换定理；当２个无穷大负等价时，给出它们和的等价代换定理．结合具体实例探讨等价代换定理在解决含无穷大和差的复杂未定式极限中的应用．

无穷大；等价；泰勒公式

极限是高等数学的主要工具，熟练掌握求极限的方法对理工科学生的专业学习非常重要，同时极限的计算也是硕士研究生考试的重点内容[1]．关于无穷大的比较及等价代换引起了国内学者的广泛关注，文献[2-4]给出无穷大比较的定义，提出了无穷大阶的概念，在２个无穷大非负等价（非等价）时利用极限运算法则研究了２个无穷大和（差）的等价代换，并推广到有限个无穷大的情况．孙卫卫[5]等在研究无穷大和差代换的基础上，进一步研究了幂指函数中的等价无穷大代换问题，给出了其在幂指函数的实例应用．李红菊[6]等利用极限运算法则研究了一类分子是无穷大差的分式未定式，得到了无穷大的差能代换的充分条件．李海霞[7]等讨论了几个常见无穷大阶的比较，重点给出了在极限计算、判定方程有根等方面的应用．张燕[8]等通过举例说明了２个相互等价的无穷大的差不一定是无穷大．王禧宏[9]和孟献青[10]讨论了利用无穷大和无穷小的关系求极限的方法．这些成果丰富了无穷大代换定理，为更好地求极限奠定了基础．目前，尚未解决的问题是２个相互等价的无穷大的差是否还是无穷大，２个相互等价的无穷大的差如何替换，以前的主要研究方法是极限运算法则和初等变形，本文利用无穷大和无穷小的关系、泰勒公式等技巧研究２个无穷大和与差的代换问题，给出寻找等价无穷大的方法和应用实例．

1　主要结果及证明

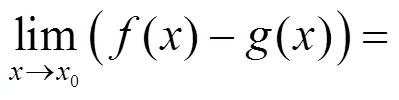
定理２的证明方法与定理1类似．

同理可以证明结论（2）． 证毕．

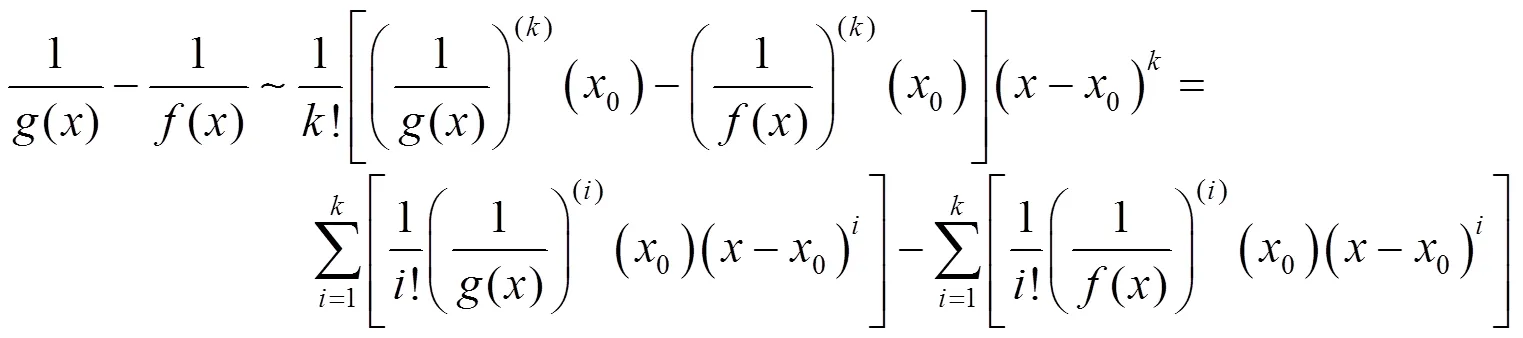
2　实例应用

[1] 同济大学数学系．高等数学：上册[M]．7版 北京：高等教育出版社，2014：52-55．

[2] 王梅英，陆伟东．无穷小与无穷大的阶在极限运算及判级数敛散性中的应用[J]．南京审计学院学报，2007，4（2）：73-76．

[3] 刘桂仙，刘庆升．求极限的等价无穷大代换[J]．高等数学研究，2011，14（1）：51-52．

[4] 张传芳．再谈关于无穷大量的等价性问题[J]．高等数学研究，2020，23（5）：5-6，9．

[5] 孙卫卫，孙建英．等价无穷大在未定式计算中的应用[J]．哈尔滨师范大学自然科学版学报，2014，30（3）：69-72．

[6] 李红菊，丁健．关于等价无穷大量代换求极限的补充[J]．长春大学学报，2015，25（10）：46-50．

[7] 李海霞，聂东明．无穷大的比较及应用[J]．山东农业工程学院学报，2016，33（10）：131-132．

[8] 张燕，程翔宇．无穷大相减极限问题求解[J]．安徽水利水电职业技术学院学报，2018，18（1）：68-70．

[9] 王禧宏．数列及函数极限不存在、无界及有关无穷大问题的讨论[J]．高等数学研究，1998（3）：25-26．

[10] 孟献青．几类常见函数的极限计算方法[J]．山西大同大学学报（自然科学版），2020，36（6）：33-36．

Equivalent substitution theorem of sum and difference of infinity and its application

TIAN Xuegang，WANG Shaoying

（School of Science，Binzhou University，Binzhou 256603，China）

The equivalent substitution of the sum and difference of infinity was studied when the independent variable tends to finite value．The sum and difference of any two infinities are firstly characterized by Taylor formula，and then the equivalent substitution theorem of their difference is given when two infinities are equivalent，and meanwhile the equivalent substitution theorem of their sum is provided when two infinities are negatively equivalent．Finally，some specific examples are given to show the application of equivalent substitution theorem in the calculation of complex indefinite form limit with infinite sum and difference．

infinity；equivalence；Taylor formula

1007-9831（2022）11-0026-06

O172

A

10.3969/j.issn.1007-9831.2022.11.005

2022-04-13

国家自然科学基金项目（61703050）——网络化随机系统的事件触发滤波与故障检测；滨州学院重点教改项目（BYJYZD201808）——新工科下基于应用型人才培养的高等数学模块化分层教学研究与实践；滨州学院教改项目（BYJYYB201733）——基于专业服务的应用型本科院校高等数学课程改革研究与实践

田学刚（1980-），男，山东邹平人，讲师，硕士，从事泛函分析和控制理论研究．E-mail：xuegangtian@163.com