基于隔震后的LNG储罐桩顶约束系数计算新方法

陈团海 彭延建 肖 立 扬 帆 刘 洋 陈严飞

1.中海石油气电集团有限责任公司 2.“油气管道输送安全”国家工程实验室·中国石油大学(北京)

0 引言

随着液化天然气（Liquefied Natural Gas，LNG）储罐技术的不断发展，储罐的罐容越来越大。目前中国石化设计的全球最大27×104m3LNG储罐已经在青岛LNG项目完成穹顶浇筑工作，中国海油设计的17座27×104m3LNG储罐也均已开工建造，其中11座已经完成了气升顶作业。由于大型LNG储罐为典型的大跨度及超高剪力墙结构，地震荷载为储罐设计的控制荷载，为了满足设计要求，包含桩基础的超大型LNG储罐均需采取减隔震措施降低地震荷载的作用。对于常规罐容（16×104m3及以下）的储罐，也有大量采用减隔震措施降低地震荷载从而提高储罐安全性，比如中国海油大鹏LNG、中国石油唐山LNG、中国石油江苏LNG和中国石化天津LNG等项目。不同于建筑结构，采用减隔震措施后由于通风需要，LNG储罐通常不会设置隔震层，而是直接在桩顶与承台之间安装隔震支座，这种减隔震设计方案使得桩基与承台之间原来的刚性约束变为柔性约束，为桩基承载力的计算带来一定困难。根据《建筑桩基技术规范：JGJ 94—2008》[1]，在计算桩基水平抗力时，需要考虑群桩效应，通过群桩系数反映，LNG储罐桩基群桩系数（ηh）通过桩相互影响效应系数（ηi）乘以桩顶约束效应系数（ηr）得到。

目前对群桩系数的研究大多集中在ηi计算方面，包括理论公式推导[2-3]、大尺度模型实验研究[4-5]及有限元数值研究[6-8]。而对ηr的研究较少，在桩基设计规范只给出了桩顶嵌入承台长度50～100 mm时的取值，本文参考文献[9-10]对规范中ηr取值与实际工程存在的差异性进行了分析，但是并没有给出确实可行的准确算法，而对于在承台和桩顶设置隔震支座这种柔性约束情况，规范没有给出明确的数值及算法，也没有文献进行过相关的研究。通过咨询《建筑桩基技术规范：JGJ 94—2008》规范编制组，给出的意见是：隔震后ηr取值应该介于1.00～2.05，在没有实验和理论研究的情况可保守考虑取1.00，有实验和理论计算的情况可以根据计算结果确定。若ηr取1.00可以大大简化计算，同时桩基承载力的计算结果也是保守的，可以确保储罐的安全性，但是同时也会造成一定的浪费，由于通常LNG储罐桩基水平承载力安全系数本身就不大，在很多场地若ηr简单取为1.00会造成桩基水平承载力计算值不满足要求，导致LNG储罐需要设置双层承台的情况，大大增加储罐建设成本及施工周期。为此，笔者根据桩顶约束系数计算原理，确定了隔震后LNG储罐桩顶约束系数计算公式及数值计算方法，并进行了参数敏感性分析，研究影响桩顶约束系数的因素及影响规律，为工程设计提供指导。

1 桩顶约束系数数值计算方法

根据《建筑桩基技术规范：JGJ 94—2008》规范编制组的意见，桩顶约束系数可以根据实验或者理论计算确定，实验方法结果准确，能够真实反映桩基受力情况，但是一旦桩基参数和地层参数发生变化，就需要重新做实验，费用和时间成本较大，不具推广性。而理论计算则可以采用数值计算方法模拟桩—土相互作用，根据桩头位移或者桩身弯矩计算桩顶约束系数，该方法可以根据每一个项目的桩基和地层参数建模计算，相比实验方法费用低、时间短，具有很好的推广性，而且在LNG储罐结构分析中，有大量采用数值方法计算且结果准确度满足要求的案例[11-15]。因此，笔者主要研究采用数值手段计算桩顶约束系数的方法。

数值计算方法第一步是验证其准确性，因此本文首先采用已有的实验结果验证数值计算方法的准确性，在满足准确性前提下再进行参数敏感性分析。《建筑桩基技术规范：JGJ 94—2008》规范编制单位建研院于2020年7月在建筑科学期刊发表了论文《桩基水平承载力群桩效应系数试验研究》[16]，该论文做了8组实验，其中桩顶自由单桩4组、桩顶承台约束1组、群桩3组，为了避免群桩相互影响效应，本次主要利用桩顶自由单桩和单桩承台约束的结果来验证数值计算方法。

1.1 计算模型的建立

根据本文参考文献[16]的实验模型建立数值计算模型，模型由土体、桩和承台组成，其中桩直径为150 mm，长度为3.5 m，配置6根直径6 mm的钢筋；承台尺寸为1.6 m×0.4 m×0.4 m，顶部和底部配置间距200 mm、直径12 mm的钢筋；土体尺寸为13.4 m×5.4 m×4.0 m，采用分层回填夯实的方法进行基础处理，每层土体的物理力学指标如表1所示。

表1 实验用土的物理力学指标表

根据以上条件采用有限元软件ANSYS建立分析模型（图1）。在模型中，采用非线性实体单元SOILD186模拟土体和承台混凝土，采用梁单元BEAM188模拟桩，采用离散钢筋单元REINF264模拟钢筋，钢筋和混凝土自动装配，土体材料本构采用DP模型。

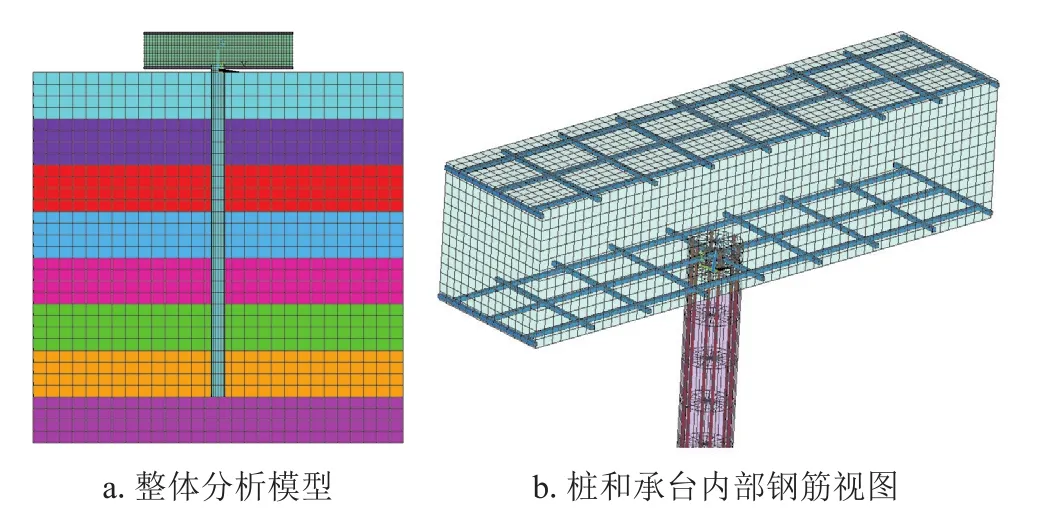
图1 数值分析模型图

1.2 计算结果及误差分析

根据本文参考文献[16]的荷载条件进行计算，确定不同桩顶荷载及桩顶约束情况下的水平位移云图如图2所示。

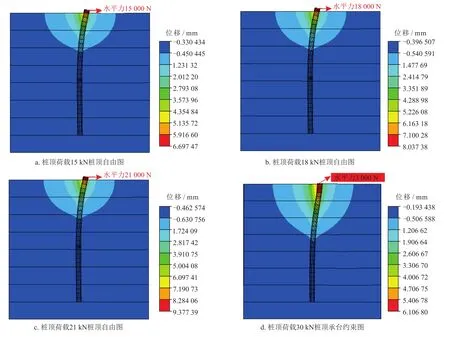
图2 不同桩顶荷载及桩顶约束情况下水平位移结果图

根据图2可以得到各个荷载作用下对应的最大位移，将最大位移与本文参考文献[14]中桩顶位移进行比较，计算数值与实验结果的误差，具体结果如表2所示。

表2 数值计算结果与实验结果对比误差表

由表2可知，数值计算结果与实验结果接近，对于桩顶自由的情况最大误差为4.203%；对于承台约束情况最大误差为6.390%。这是因为在承台上加载及承台与土体上表面的作用存在一定的不确定性因素导致误差增大，但是整体误差在可接受范围之内，说明数值计算模型是可靠的。

利用以上数值模型计算出桩顶自由和桩顶承台约束情况的位移或者弯矩，根据桩基规范计算即可确定桩顶约束系数。

2 隔震后桩顶约束系数的计算方法

2.1 计算公式的确定

桩顶约束系数的计算本质是桩顶完全自由情况下桩顶或者桩身力学响应结果与桩顶在施加一定约束情况下对应结果的比值，在《建筑桩基技术规范：JGJ 94—2008》中给出了桩顶嵌入承台深度5～10 cm时桩顶约束系数的计算公式，根据以位移控制和以强度控制两种情况分别给出了以位移和弯矩作为力学响应结果的计算公式。

以位移控制时，桩顶约束系数的计算如下：

以强度控制时，桩顶约束系数的计算如下：

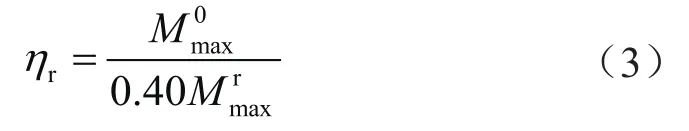
式（2）、（3）中系数1.25和0.40是考虑桩顶嵌入承台深度5～10 cm这种非完全嵌固相比完全嵌固对桩顶约束程度削减而设的系数，因为通常采用公式或者数值计算时只能计算得到桩顶完全嵌固这种约束条件下的位移和弯矩，而难以得到桩顶嵌入承台深度5～10 cm这种非完全嵌固约束条件下位移和弯矩的准确结果。

而对于桩顶设置隔震支座这种情况，采用数值方法可以准确地模拟桩顶约束情况，故可以通过数值方法准确计算出桩顶位移和桩身弯矩，因此计算桩顶约束系数时只需要比较桩顶设置隔震支座这种柔性约束与桩顶完全自由这两种约束条件下桩顶位移或者桩身弯矩即可，由于柔性约束条件桩身位移和弯矩分布情况与桩顶自由时基本一致[17-18]，不再需要转换。因此，隔震后桩顶约束系数计算如下，以位移控制时，隔震后桩顶约束系数的计算公式为：

以强度控制时，隔震后桩顶约束系数的计算公式为：

2.2 数值计算方法

前面已经给出了非隔震情况下桩顶约束系数的数值计算方法，并且结果可靠；对于隔震情况，只需要在桩顶增加隔震支座，隔震支座里面的橡胶为非线性材料，计算时需要充分考虑非线性，而材料非线性特性可以通过支座大变形实验的滞回曲线得到[19-20]，隔震支座可以采用ANSYS的非线性弹簧单元COMBIN40进行模拟[21-24]。在前面模型基础上增加直径100 mm的隔震支座，支座力学参数如表3所示，建立的隔震后桩顶约束系数计算模型如图3所示。

表3 隔震支座力学参数表

图3 隔震后桩顶约束系数计算模型图（1/4剖面）

对模型中承台施加15 kN水平力进行计算，得到整个模型的水平位移云图如图4所示。

图4 隔震后水平位移结果图

由图4可知，隔震后承台位移远大于桩头的水平位移，承台的最大水平位移达到9.259 mm，桩头的位移为5.926 mm，这是因为隔震支座发生了较大的变形。而由图2-a可知桩头自由时施加水平荷载15 kN对应的桩头水平位移为6.697 mm，按照式（3）位移控制公式，可计算得到ηr为1.130。

若考虑按照强度控制，则可提取桩顶自由及隔震两种情况桩身的弯矩云图（图5、6），由图可知，桩顶自由时桩身最大弯矩为4.829 kN·m，隔震后桩身最大弯矩为4.246 kN·m，根据式（5）可计算得到ηr为1.137，对比可知采用按照位移控制和按照强度控制计算的桩顶约束系数基本相同。

图5 桩顶自由时桩身弯矩云图

图6 隔震后桩身弯矩云图

3 参数敏感性分析

为了更好指导LNG储罐的减隔震设计，研究隔震后桩顶约束系数的影响参数及参数敏感性。根据桩顶约束机理，桩顶约束系数的大小可能与桩顶、桩身约束结构的刚度及桩本身的刚度相关，对桩顶的约束刚度主要体现在隔震支座水平刚度；而桩身的约束刚度主要体现在土体刚度方面，可以土壤的弹性模量进行表征；桩本身的刚度在材料和配筋不变的情况下主要与尺寸相关，在长度不变的情况下改变桩径即可改变桩的刚度。另外桩顶约束系数除与刚度相关，还可能与外部荷载相关。

综合以上分析，主要研究隔震支座水平刚度、土壤弹性模量、桩径以及桩顶水平荷载对桩顶约束系数的影响规律。以表1中的土壤弹性模量、表2中的隔震支座刚度、桩径150 mm、桩顶水平荷载15 kN为基准，对这些参数比例缩放计算桩顶约束系数变化规律并绘制曲线，结果如图7～10所示。

图7 隔震支座等效刚度影响曲线图

图8 土壤弹性模量影响曲线图

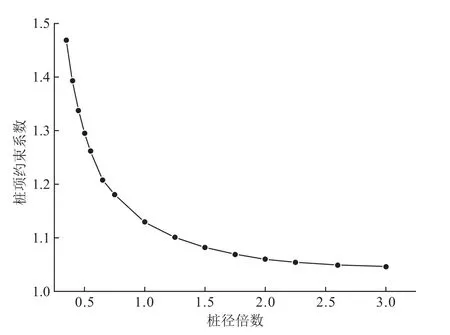
图9 桩径影响曲线图

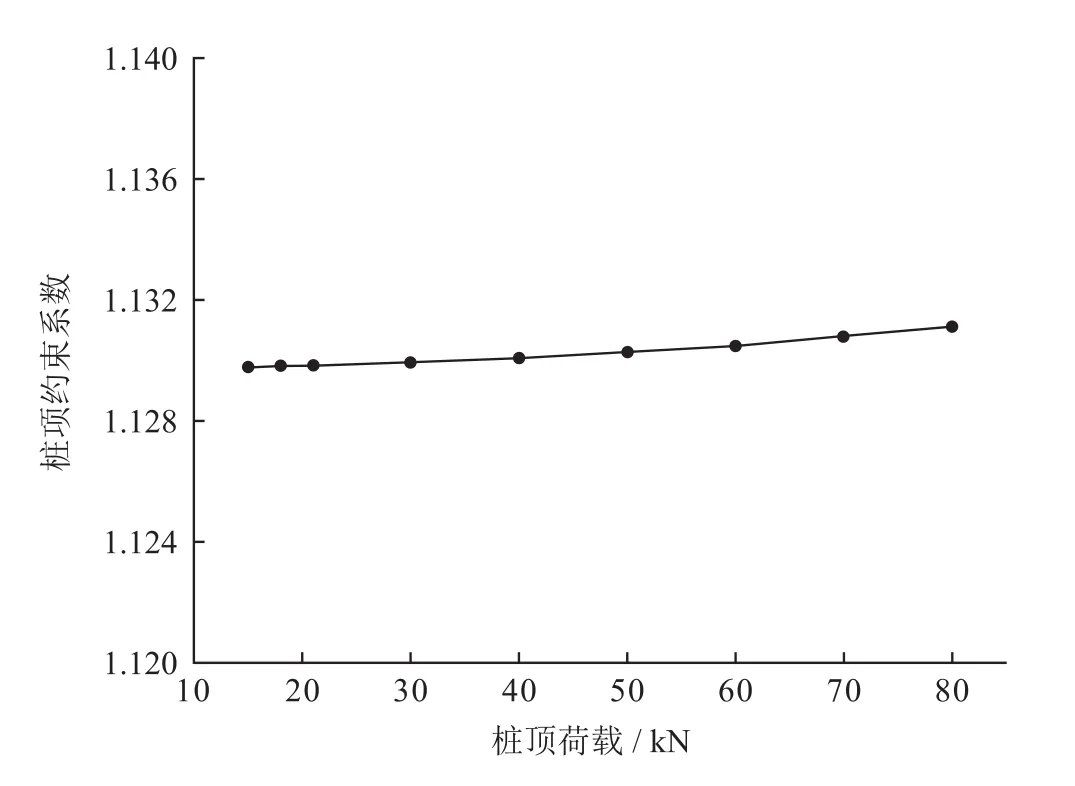
图10 桩顶荷载影响曲线图

由图7可知，随着隔震支座等效刚度的增加，桩顶约束系数几乎保存不变，因此可以认为隔震支座水平刚度对桩顶约束系数无影响，这是因为隔震支座主体为橡胶材料，其刚度远小于混凝土材料，作用在承台的水平荷载通过隔震支座完全传递至桩头，并且支座对桩头几乎没有约束作用。

由图8可知，随着土壤弹性模量的增加，桩顶约束系数呈线性化增加的趋势，这是因为土壤刚度越大对桩身的约束越强，桩头的变形越小，相应地桩顶约束系数增大。

由图9可知，随着桩径的增加，桩顶约束系数以幂函数形式快速减小，这是因为桩径越大，在桩身材料和桩长不变的情况下桩的刚度快速增加，但是土壤刚度不变，土壤相对于桩来说变软，对桩的约束力下降，因此桩顶约束系数下降。

由图10可知，随着桩顶荷载的增加，桩顶约束系数略有增加，但是增加量可以忽略不计，荷载增加6倍之后，桩顶约束系数只增加了0.1%，因此可以认为桩顶荷载对桩顶约束系数无影响。

由以上分析结果可知，不同条件下的桩顶约束系数介于1.05～1.50，在进行LNG储罐减隔震设计时，增加隔震支座刚度并不会增大桩顶约束系数；而对于地层条件好的场地，除了地层承载力大以外，隔震后桩顶约束系数也大，桩基承载能力强，这种场地适合采用减隔震措施；当储罐建造场地条件确定以后，设计时适当降低桩直径能够大幅提高桩顶约束系数，从而提高整个储罐桩基础承载力；而储罐自身受到的荷载对桩顶约束系数及桩基础承载能力没有影响。

4 结论

针对规范中没有规定桩顶柔性约束条件下桩顶约束系数计算方法的问题，研究了采用数值计算确定隔震后LNG储罐桩顶约束系数的方法，首先利用实验结果对数值计算结果的准确性进行验证，其次根据桩顶约束系数计算原理确定了隔震后桩顶约束系数的计算公式并研究了数值计算方法，最后对桩顶约束系数进行参数敏感性分析，确定了影响的关键因素，得到以下结论。

1）LNG储罐隔震后，采用位移控制和强度控制的方法计算桩顶约束系数结果基本一致，其值介于1.05～ 1.50。

2）地层条件及桩径对桩顶约束系数有较大的影响，随着地层土体弹性模量的增加桩顶约束系数线性增大，而随着桩径的增加桩顶约束系数以幂函数形式减小。

3）隔震支座的力学性能及外部荷载对桩顶约束系数没有影响。