考虑多种约束类型的放射状集输管网布局优化研究
2023-01-13杨永兴梁昌晶
肖 娟,李 军,杨 港,杨永兴,孙 晔,梁昌晶
1.中国石油华北油田公司第一采油厂,河北任丘 062552
2.中国石油华北油田公司二连分公司,内蒙古锡林浩特 026000
3.华北油田华港燃气集团有限公司,河北任丘 062552
集输管网作为油气田生产的重要组成部分,其设计不仅要满足开发规模和布局要求,还要考虑自身的经济性和运行的稳定性[1]。集输管网中的流量、压力、温度等数据属于连续变量,管径、管网连接方式等属于离散变量,同时井口与计量站、计量站与集中处理站的连接方式会随生产井数量的增加呈指数增加,故集输管网布局优化是一类混合整数非线性规划(MINLP)问题,已被学者证明是NP-hard完全问题[2-3]。对于管网布局优化的求解,一种是采用传统的Dijkstra算法[4]、Floyd 算 法[5]、Kruskal算 法[6]、Prime 算法[7]等,这些算法虽原理不尽相同,但均基于穷举法,其运算量是时间复杂度的平方,当管网复杂时,运算时间不能满足生产需求。另一种是采用群智能优化算法求解,王博弘等[8]以管网总费用最低为目标函数,采用遗传算法(GA)对环枝状结构的管网局部进行优化;王昊等[9]通过果蝇算法(FOA)中的群体位置变化对放射状气田集输管网进行优化;黎彬等[10]采用粒子群算法(PSO)对管网进行优化。智能算法在求解布局优化问题时可以从多点搜索,增加最优解的可靠性,但智能算法不依赖于拓扑优化的数学性质,在搜索时具有随机性和概率性,导致其在求解上存在不稳定性、易陷入局部最优解等问题。此外,前人对于管网布局多为分步优化计算[11-12],即按照布站方式,从下向上逐级递进优化,其分步优化结果得到的是局部最优解,与多约束类型下的全局最优解尚存在一定差距[13]。基于此,以计量站、集中处理站、管道投资费用最少为目标函数,建立受约束下的放射状集输管网布局优化模型,采用混沌差分算法对其求解,并对比分步优化和整体优化,得到集输管网各部分的投资费用,以期指导油气田地面工程设计,降低初步设计和施工图设计投资概算。
1 数学模型
根据油气田现场实际情况,结合图论和最小生成树的相关知识,将管网结构分为枝状、环状和放射状。放射状布局适用于面积较大、井较多、油藏面积分散的油田,其运行稳定性较环状和枝状好,是目前油气田集输管网布局最常用的拓扑形式。在此以放射状管网为基础,定义井到计量站或集中处理站的管道为一级管道,计量站到计量站/集中处理站的管道为二级管道,以站和管道建设费用最少为目标函数,公式如下:
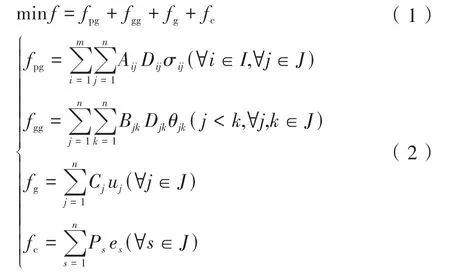
式中:minf为总投资费用最少函数,元;fpg为一级管道投资,元;fgg为二级管道投资,元;fg为计量站投资,元;fc为集中处理站投资,元;Aij为第i口井到第j个站的一级管道单位价格,元/m;Dij为第i口井到第j个站的一级管道长度,m;σij为第i口井到第j个站的状态变量,连接时取1,未连接时取0;Bjk为第j个站到第k个站的二级管道单位价格,元/m;Djk为第j个站到第k个站的二级管道长度,m;θjk为第j个站到第k个站的状态变量,连接时取1,未连接时取0;Cj为一个计量站投资,元;uj为计量站状态变量,取值为1和0;Ps为一个集中处理站投资,元;es为集中处理站状态变量,取值为1和0。其中,I、J分别为井和站的集合;m、n分别为井和站的数量。
2 约束类型
2.1 隶属关系约束
在放射状集输管网中,低级别的节点只能与一个高级别的节点相连,但高级别的节点可同时与多个低级别的节点相连,即每个井只隶属一个计量站或集中处理站,公式如下:

2.2 集输半径约束
集输半径约束表现为水力条件和热力条件,一方面要求井口回压不超过2 MPa,另一方面要求单井产液进站温度高于凝点3~5℃,故每条一级管道长度不能超过最大集输半径Lmax,公式如下:

2.3 处理量约束
为保证流量分配平衡,计量站和集中处理站的设备需满足最大处理量约束Qmax,以便达到较好的分离效率,公式如下:

式中:qi为第i口井的流量,m3/d;Qmax为站的最大处理量,m3/d。
2.4 井式约束
站内汇管通常具有一定的连头数量要求,不能超过最大连头数量Nmax,公式如下:

2.5 拓扑关系约束
井和站连接以及站和站连接时需保证井、站必须存在,且二级管道数量较站(计量站+集中处理站)的数量多1,防止二级管道形成星状和环状结构,公式如下:

2.6 集中处理站数量约束
集输管网拓扑关系中,定义集中处理站的数量为1,公式如下:

3 混沌差分算法求解及步骤
差分算法是为解决Chebyshev多项式提出的基于群体差异信息的启发式智能算法,包括变异(将解的一部分改变)、交叉(几个解之间互换)和选择(是否在下次迭代中保留当前解)等操作[14]。但差分算法与遗传算法类似,易出现早熟现象,且无法平衡全局开采与局部搜索,对于群体之间竞争与协作关系的统筹较差,考虑到Logistic混沌映射具有较强的遍历性,可提高初始种群多样性,故将混沌理论融入差分算法[15],其变异操作为:
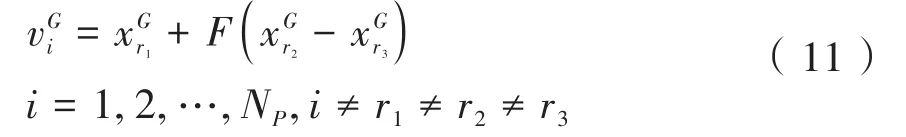
式中:viG为目标个体i在G次迭代中对应的变异个体;为种群在G次迭代中的3个互不相同的个体;F为缩放因子;Np为种群数量。其中,F的取值为定值,取值范围[0,1],导致种群多样性不足,故将混沌算法替代F,公式如下:

式中:zk为第k次产生的混沌序列值,μ为控制参数。当μ=4时,标准Logistic混沌映射产生的混沌分布均匀性最好,遍历性最强。
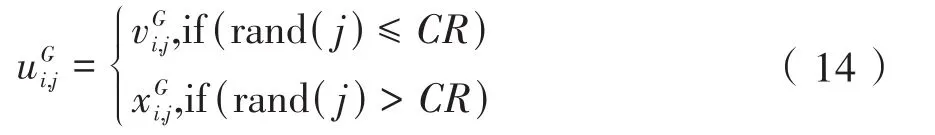
式中:ui,jG为目标个体i在j维上在G次迭代中对应的交叉个体;CR为交叉因子,取值范围[0,1];D为算法维度;rand()为[0,1]的正态随机数,确保交叉后的个体至少有一维变量由变异个体提供。
在交叉操作后完成个体之间的选择操作,从目标个体和试验个体中选择最优的值作为下一代,公式如下:
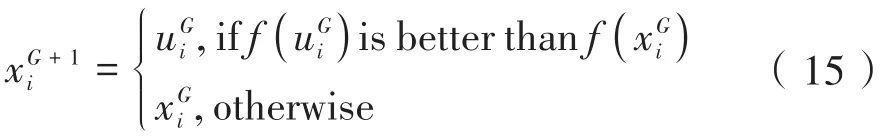
混沌差分算法(CGLSDE)的求解步骤如下。
(1)初始化参数,包括种群大小、维度、交叉因子、最大迭代次数、约束类型和决策变量的阈值、混沌局部搜索次数等。
(2)对种群中的每个个体进行评价,选出适应度最好的个体作为当前种群的最优解,此时迭代次数为1。
(3)根据式(12)、(13)进行变异操作,根据式(14)进行交叉操作。
(4)根据式(15)进行选择操作,如选择后的个体适应度优于当前种群最优解,将最优解替换。
(5)不断重复上述步骤(2)~(4)操作,当迭代次数等于最大迭代次数,或适应度值达到设定阈值时,迭代停止,算法完成。
4 实例分析
4.1 考虑单个约束类型
在油气田集输管网设计中,需遵循本文第2章提出的约束类型设置,考虑集输半径、处理量和井式约束对拓扑形态的影响。当地面系统投资过大时,只能减少计量站和集中处理站的投资,但可能导致部分计量站的处理量超标或集输半径不满足要求,故三者之间是相辅相成且互相依存的。在此先考虑单个约束类型对集输管网布局的影响,以30×104t/a产能的区块为例,各部分的投资定额见表1,油井产量和井位坐标见表2。

表1 集输系统各部分投资定额
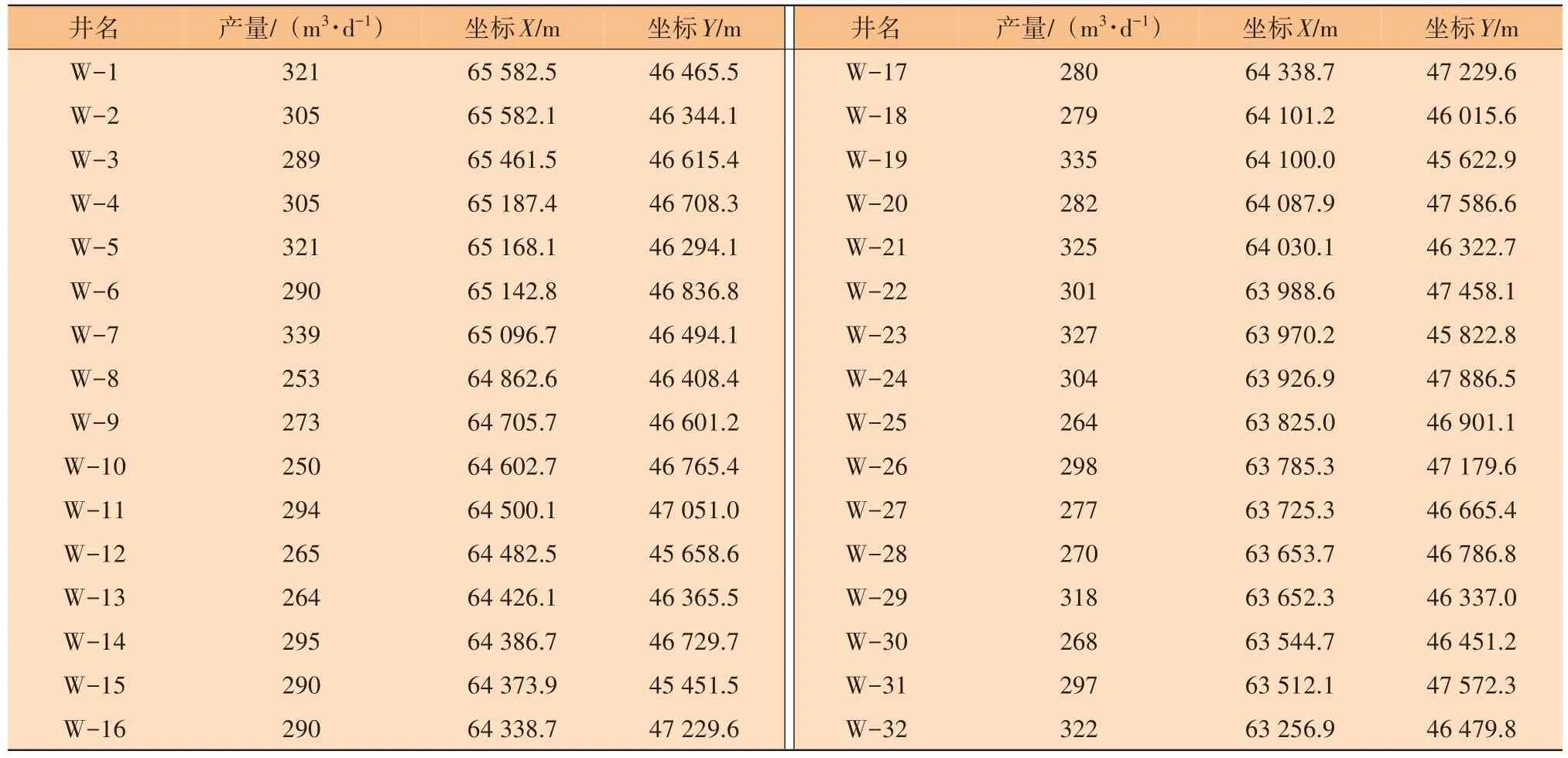
表2 各油井产量
设置CGLSDE算法种群,大小为40、维度为3、交叉因子为0.5、最大迭代次数为100,总的混沌搜索次数和局部搜索次数分别为8和4,每个问题求解10次,对单约束类型下的管网布局进行求解,不同约束类型下的集输管网投资明细见表3,管网布局见图1。

表3 不同约束类型下的集输管网投资
当只考虑处理量约束时,分别在W-25、W-10、W-16和W-7井上建立4座计量站,在S2计量站的基础上建立集中处理站,S1、S3、S4站的来液通过二级管道汇入集中处理站。其中,S1、S2、S3和S4站的油井来液分别为2 598 m3/d、2 572 m3/d、2 423 m3/d和2 339 m3/d,均未超过约束限值,说明模型运行成功。但从图1(a)中可见距离S1站较近的W-27、W-29井未接入S1,却接入了距离较远的S2站,同理距离S3站较近的W-21井未接入S3站,却接入了距离较远的S2站,这保证了各站以最大处理量方式运行,但距离较远会使采出液温降过大,如W-27、W-29到S2站的距离分别为883 m、1 042 m,均超过了最大集输半径800 m的限值要求。此外,生产井以放射状结构布局,站间以枝状结构连接,形成了二级放射状管网布局,证明了模型算法的准确性和科学性。
如图1(b)所示,当只考虑集输半径约束时,此时的管网布局与只考虑处理量时截然不同,在S3计量站的基础上建立集中处理站,S1站的来液汇聚到S2站后进入集中处理站,S4站来液直接汇入集中处理站。其中,W-11井距离S1站的距离最远为653 m,未超过Lmax,说明模型运行成功。S1、S2、S3和S4站的油井来液量分别为2 055 m3/d、1 719 m3/d、2 670 m3/d和2 940 m3/d,S3、S4站的流量超过处理量限值,且不同站间的流量分配不均,当油气田滚动开发时,S3、S4站附近的新增加密井无法接入系统,而S2站处理的余量又太大,造成资源浪费。
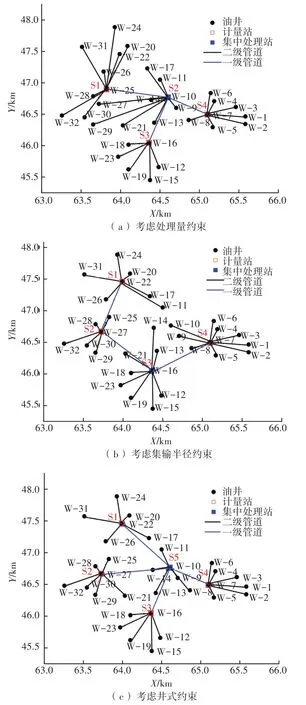
图1 不同约束类型下的集输管网整体优化布局
如图1(c)所示,当只考虑井式约束即站内连接头数量时,各站均在井组中心,计量站数量为5,且在S5计量站的基础上建立集中处理站。S1、S2、S3、S4和S5站的连头数量分别为6、7、6、7、6,均未超过井式约束,说明模型运行成功。此约束类型下不存在集输半径的影响,但计量站数量增加,与处理量约束类型相比,一级管道长度减少,二级管道长度增加,导致总投资在三种单约束类型中最大。
综上所述,单独考虑任何一种约束类型均不利于集输管网的经济性和稳定性。
4.2 整体优化和分步优化对比
综合考虑集输半径、处理量和井式约束对拓扑形态的影响,进行整体优化求解,约束类型如表3所示,同时对比其与分步优化求解的结果,即先进行集输半径,再依次进行处理量和井式约束优化求解,整体优化与分步优化结果对比见表4,管网分步优化布局井组划分见图2,管网整体优化布局井组划分见图3。经核算,两种优化方式的结果均满足约束条件,按照单井和计量站的关系划分井组,两种优化方法均划分了5个井组,但每个井组所辖的井号不同。井组2在两种优化方式中所辖油井相同,但管网连接方式不同,计量站位置也不同;整体优化中属于井组5的W-17井在分步优化中属于井组1,整体优化中属于井组3的W-13井在分步优化中属于井组5,整体优化中属于井组5的W-8井在分步优化中属于井组4,可见不同优化方法的结果直接影响站点布局、一级管道和二级管道的长度,最终影响管道投资。分步优化与整体优化相比,一级管道长度变短,二级管道长度变长,这是由于分步优化先以一级管道长度最小为目标函数求解,而整体优化在两级管道中有所取舍,造成一级管道的投资较大。整体优化较分步优化总投资降低了16.44万元。
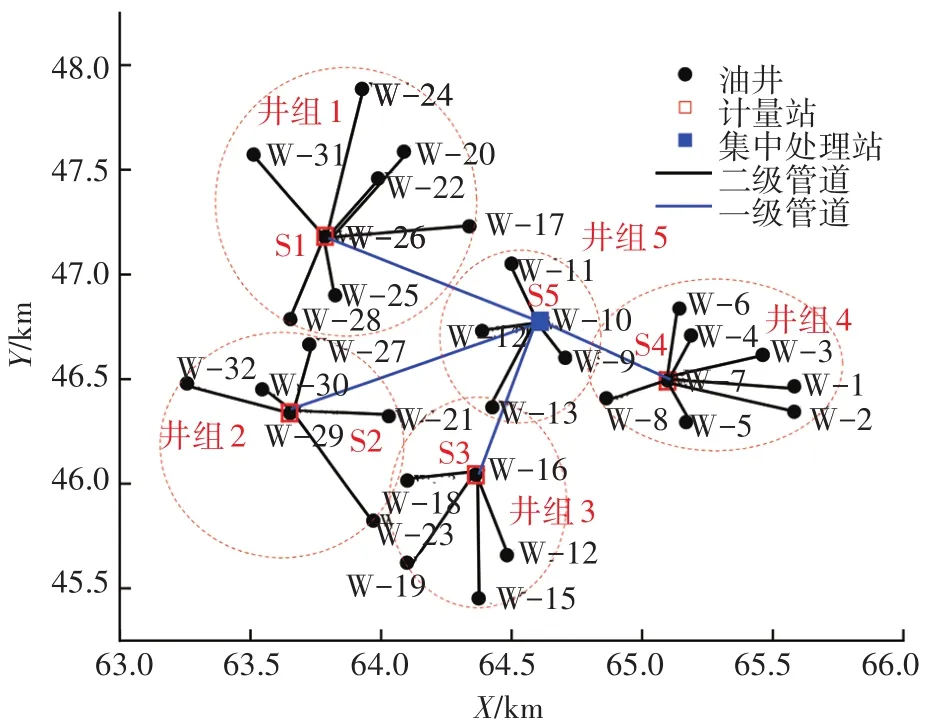
图2 分布优化布局井组划分

图3 整体优化布局井组划分

表4 整体优化和分步优化结果对比
以整体优化结果中的总投资为基准,与表3中的单约束类型的优化结果进行对比,集输半径、处理量和井式约束的总投资变化率分别为-1.61%、-1.82%和0.16%,说明对集输管网投资影响最大的为处理量,其次为集输半径和井式约束。
4.3 求解方法对比
为验证CGLSDE算法的准确性,分别采用GA、FOA和PSO算法进行对比,其参数设置与文献一致,以一级管道长度为例,取10次求解中的最大值、最小值、平均值,并比较标准差和迭代稳定后的平均计算时间,如表5所示。从求解精度上考虑,CGLSDE算法的最大值、最小值和平均值均为11 308 m,其余算法的结果均比CGLSDE算法大,说明CGLSDE算法的总投资结果较小;从求解稳定性上考虑,标准差越小,算法稳定性越强,CGLSDE算法的标准差较其余算法小了两个数量级,说明CGLSDE算法在求解稳定性上有明显优势;从计算时间上考虑,CGLSDE算法较其余算法计算时间大幅减少,降低约73%~76%,这在大型集输管网优化求解中是难得的。CGLSDE算法的迭代历史见图4,10次求解过程均在30次左右收敛至最优解附近,求解速度较快,收敛后10次结果的管道长度相差不超过0.05 m,说明该算法具有很好的鲁棒性和科学性。
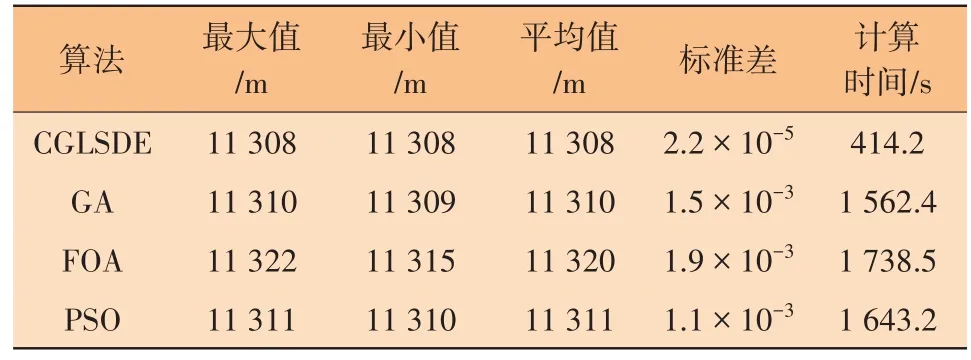
表5 不同算法对比结果
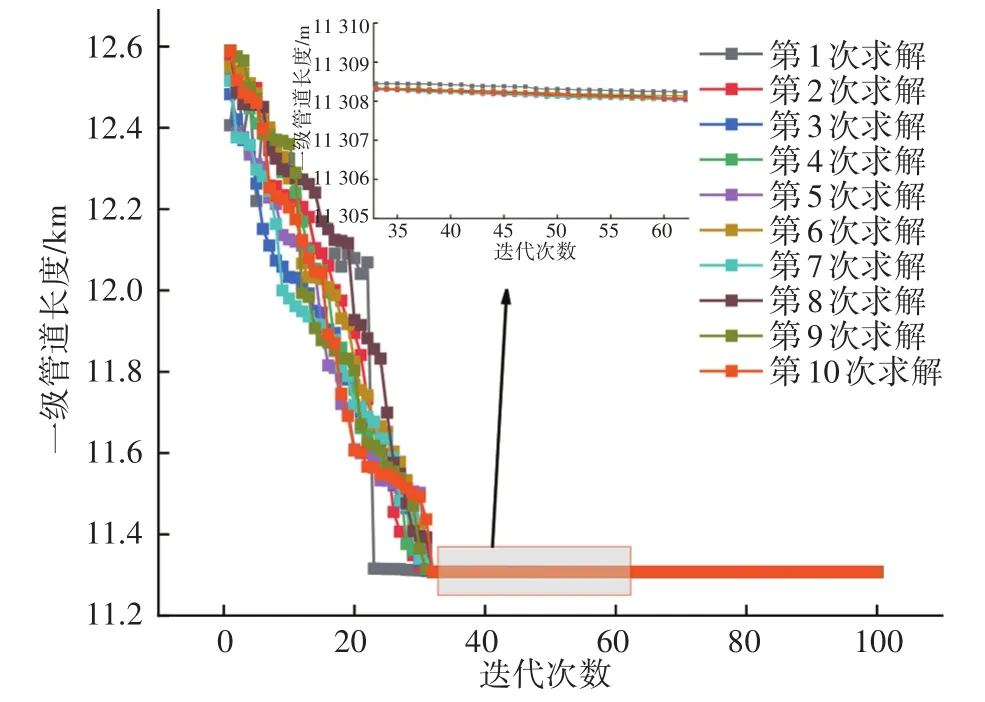
图4 CGLSDE算法的迭代历史
5 结论
(1)针对集输管网优化布局这类NP-hard完全问题,建立以站和管道费用最少为目标函数的混合整数非线性规划模型,通过约束条件限制,采用CGLSDE算法对其进行求解,获得站点位置、管网拓扑形态以及各部分对应的投资组成。
(2)单独考虑任何一种约束类型均不利于集输管网的经济性和稳定性,其中单独考虑井式约束时不存在集输半径的影响,但计量站数量增加,导致总投资在3种单约束类型中最大。
(3)整体优化和分步优化的结果具有相同的井组数量,但每个井组所辖的井号并不相同;整体优化得到的是全局最优解,其总投资较分步优化有所降低。
(4)CGLSDE算法在求解精度、稳定性、计算时间和迭代次数等方面较GA、FOA和PSO算法具有明显的优势,证明了该算法的鲁棒性和科学性。
(5)以上研究可用于平原地区的集输管网布局,后期应加入三维地形、坡面坡度、自然障碍等因素的影响,使集输管网在考虑经济性的同时也考虑风险性。
