防渗墙“柔性材料”的研制

包承纲

（长江科学院，湖北 武汉 430010）

前文[1]已述及，三峡二期深水围堰是一座具有挑战性的工程，该围堰相当复杂，采用风化砂水下抛填堰体和防渗墙防渗的方案，即堰体先是将风化砂在60 m水深中抛填，出水后，上部30 m高度采用干填法施工。形成堰体后，依高度的不同，在堰体中轴线附近打1道或2道防渗墙。由于堰体比较庞大，边坡也较平缓，因此，围堰的静力稳定问题不大，也就是说，常规土石坝设计中主要的计算之一，即边坡整体稳定分析无大困难，但它的工作性状却很难预测，尤其是防渗墙体的应力应变状况比较复杂，而它对围堰的安全又十分重要。这个预测只有采用数值分析法才有可能[1]，这种技术在当时（20世纪80年代初）的我国才刚刚开始研究应用。

不难想像，防渗墙墙体在水压力和堰体土压力的作用下，会向下游弯曲，而由于防渗墙是插在不密实的风化砂堰体中的，因此，墙体必然产生较大位移，并存在较大的弯曲应力，上游面为拉应力，下游面为压应力。根据有限元计算，若采用常规混凝土，防渗墙墙体的应力状况不良，底部存在较多的塑性区，且上下游贯通，故其安全性堪虞。因此我们曾想以“强身固体”的思路来解决问题，即增加墙体的刚性和强度。但计算表明，此法并不奏效。据分析，增加墙体弹模并未改善其工作状况。经过多次分析，感悟到墙体的应力和变形主要受庞大的堰体控制，而增加这么大堰体的刚度又谈何容易！这样就只好转而采用“柔”的思路，即降低墙体材料的刚度，增大其柔性，以加强其承受变形的能力，而且该刚度必须大幅度的降低，但同时还必需保证材料一定的初期强度，因为墙体高度近90 m，墙体还要受到两侧风化砂堰体负摩擦力的作用，墙体内存在一定的应力。这样性能的材料就不是一般常规混凝土可以满足的。因此，研制一种“低弹高强”较为柔性的墙体材料就成为十分关键的任务。当时工程施工已在进行，这种柔性材料必须尽快进行攻关，研制出来，时间紧迫，施工不等人。

具体需要什么样的“低弹高强”材料？这仍需依仗有限元分析才能回答。经过多次敏感性分析计算，若材料的性能达到下列要求：弹性模量≤1 000 MPa；初期强度R28≥4 MPa（深槽部位为5 MPa），即模强比为250（或200），则墙体的应力和变形可以过关。而渗透系数需达K≤10-7cm/s。因此，这就成为所需材料的攻关目标。由于这种材料的模量很低，而强度又有一定要求，因此，此非一般“塑性混凝土”可以归属。同时，考虑到它的原材料主要是易碎的花岗岩风化砂，并无其它粗骨料，因此，就把它称为“风化砂柔性材料”，简称“柔性材料”。柔性材料中其它的成分还有黏土和水泥以及少量的添加剂。试验表明，这种柔性材料的特性既不同于混凝土（或塑性混凝土），也不同于土，但较接近土的特性，故研究分析中可以借用土力学中的有关原理和方法。

要研制这样的材料殊非易事，因为上述的性能要求并不简单，而围堰施工在即，时间紧迫。为此，长科院动员了搞材料和化学方面的研究力量与土工研究人员一起，在室内和现场多地，同时展开了研制工作。以室内试验为先导，进行了三百多次的配方试验，找到若干组优化配方，然后在高坝洲、隔河岩电厂围堰工地、三峡一期围堰等几个工地现场进行中试和初步应用。其后，再回到室内进行配方优化和理论研究，如此反复几次，最后获得了合乎要求的最优配合比。

柔性材料配合比是指单位体积柔性材料中，水泥、黏土、风化砂3种主要原材料的用量（以每立方米的公斤数表达），以及水胶比（水/（水泥+黏土））的值。

鉴于柔性材料中有3种主要成分，这样在配方优化研究中就形成了3因素10水平的试验方案。该3因素10水平的试验组合，共有1 000组，这么大的试验组数是难以进行的，为此需进行专门的试验设计来挑选有代表性的试验点。这种试验设计的方法有多种，不同的方法有不同的精度和工作量，例如最常用的是正交设计法，其特点是“均匀分散，整齐可比”。但3因素10水平试验若用正交设计理论，仍需进行至少100组配比试验，工作量仍然太大，因此必需寻求新的试验设计理论，如此一来当时诞生不久的均匀设计法就被选中。

均匀设计是中科院数学所王元、方开泰于1978年提出的一种崭新的试验设计方法，近年来应用表明，它非常适合于多水平的试验设计。“均匀设计是只考虑试验点在试验范围内均匀散布的一种试验方法”，它的数学原理是数论中的一致分布理论。均匀设计挑选试验点的出发点是“均匀分布”而不是考虑“整齐可比”，因而与正交设计相比可大幅度降低试验工作量，这一点使得均匀设计特别适用于多因素多水平的试验设计。例如，当试验中有s个因素，每个因素有q个水平，则共有qs种组合，正交试验方法是从这些组合中挑选出q2个点，而均匀设计法是利用数论中一致分布理论选取q个点，并用这q个点进行试验，其效果与全面试验相近。由于应用数论方法使试验点在积分范围内散布得十分均匀，因此便于计算机统计建模。均匀设计的试验布点有一套严格的计算方法，而在应用中已有预制好的均匀设计表可直接查用[2]。

对于这里的柔性材料只需做 10组试验，例如其第1组试验为：C1A7F5，即水泥C取第一水平，黏土A取第七水平，风化砂F取第五水平，对应这些水平的材料重量各为：水泥180 kg/m3，黏土150 kg/m3，风化砂1 400 kg/m3。其余9组试验情况不再赘述。

10组初选配比中有 3组配比较优秀，即C6A9F8、C7A5F2和C9A8F1，它们28 d的抗压强度分别为3.09 MPa、4.24 MPa 和3.87 MPa，初始切线模量分别为800 MPa、1 110 MPa 和920 MPa，模强比分别为258、262和237。即该3组配合比的强度指标和模强比指标均接近初期的攻关目标，只是其中后2组的初始切线模量略高，但可以进一步调整改善。由此表明上述试验设计基本是成功的。

其次研究配比与力学指标的关系，并依此建立柔性材料配合比模型。

对于建立柔性材料配合比模型，常规的统计方法并不合适，主要原因如下：

（1）一般的统计方法均是先确定数学模型然后进行统计，而柔性材料是一种复杂的材料，很难预知用什么模型来反映柔性材料配合比与其力学参数的关系；

（2）多元统计法和逐步回归法将统计信息包含在为数较少的回归系数内，此外非线性度也不够，难以反映柔性材料的复杂特性；

（3）一般的统计方法只能建立单因变量的统计关系，而柔性材料中强度与模量是一对不可分割的数据，希望能建立双因变量模型。

10组初选配比的试验结果隐含了柔性材料的原材料含量与其力学参数的关系。例如柔性材料中水泥、风化砂的含量与其强度、模量呈正相关关系，而黏土含量与强度、模量则呈反相关关系，但这种定性规律尚不足以有效地指导配比优化，为此，我们建立了一种定量或半定量的模型，据此来优化柔性材料的配合比。

近年来广泛应用的人工神经网络（简称ANN）技术具有很强的非线性映射能力，它本身就是一个模型，通过网络内部权值的调整来拟合系统的输入输出关系，即只根据输入数据和输出数据反映十分复杂的关系，网络的输出端点个数不限，因而很适合于多因变量、多自变量统计中的建模。我们采用人工神经网络技术来建立柔性材料配合比（原材料含量）与其力学参数之间的模型[3]，图1是水泥用量分别为280 kg/m3，290 kg/m3时的配合比图谱。

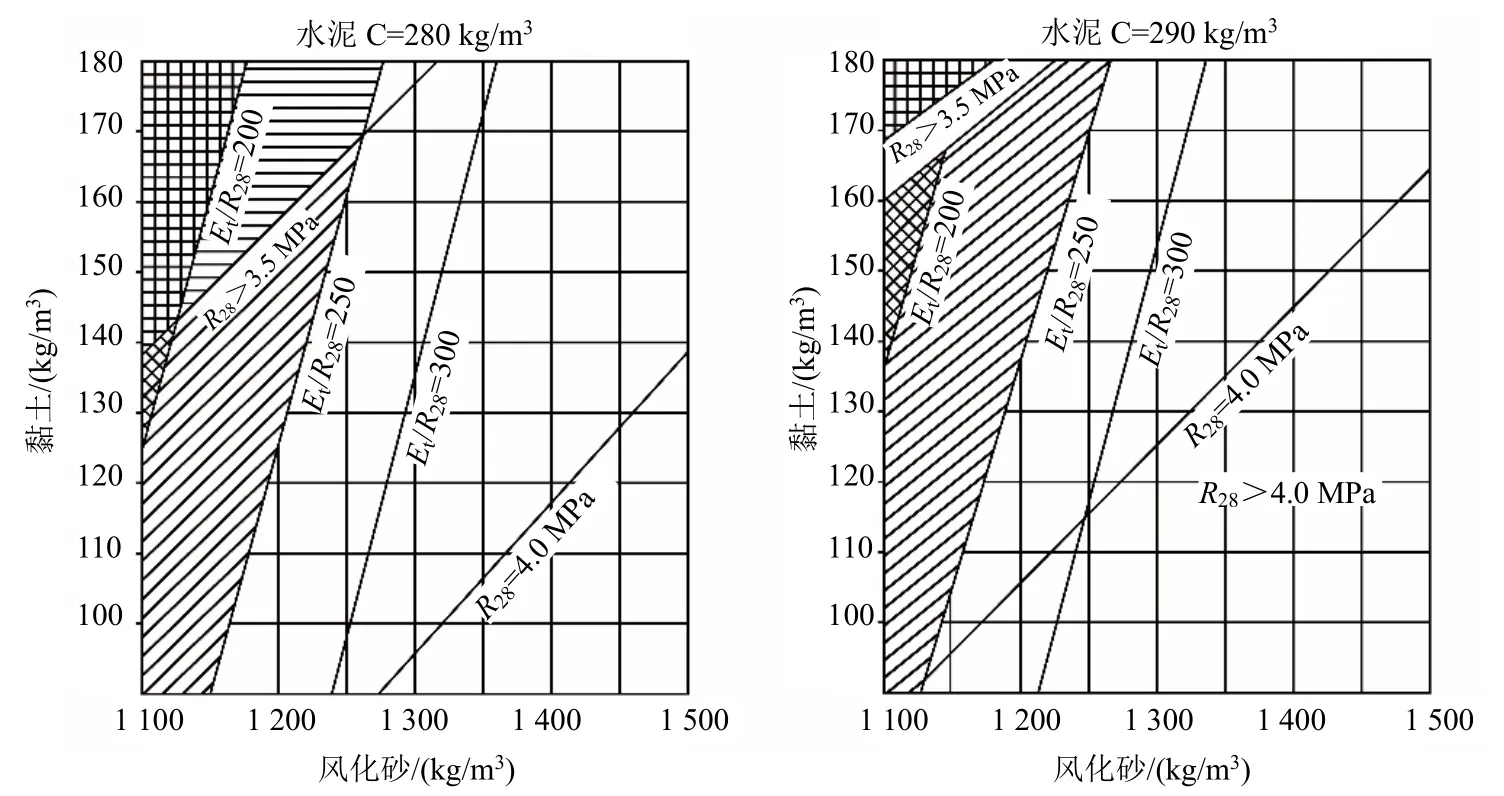
图1 柔性材料配比图谱（水泥用量分别为280 kg/m3，290 kg/m3）Fig. 1 Proportion map of flexible material (the cement dosage is 280 kg/m3 and 290 kg/m3, respectively)

图谱非常直观地表达了在给定的强度和模强比要求下，柔性材料的3组分重量的依从关系，因此根据不同的力学指标要求可以很方便地从图谱中查到所需的柔性材料配合比。据此可达到优化配合比的目的。该图是依固定水泥用量而绘制的，当然也可以将黏土或风化砂含量固定而形成类似的图谱，同样可以达到优化配合比的目的。

清华大学土力学研究者对柔性材料（TKF2）用于二期围堰防渗墙的安全性进行了邓肯-张 E-B模型（j=l）和E-μ模型（j=2）的计算复核。计算结果表明，墙体最大应力水平为：在应力集中区为0.7，在非应力集中区为0.6左右，相应安全系数分别为1.7左右，按摩尔-库仑强度准则判断，用柔性材料构筑三峡二期围堰防渗墙是安全的[4]。

研究发现，添加剂对获得“低弹高强”的性能十分重要。合适的添加剂在使土的性质发生化学变化的结构中，可以形成连续的黏合料，这种黏合料使土颗粒内部的黏结力很坚固，形成具有天然材料中所没有的性质优越的材料。本次选用的添加剂为硫酸钠早强剂，可以提高早期强度50%～100%。除上述添加剂外，也适当加入了少量减水剂，以改变水泥的水化进程，促进水化矿物晶体的成长，改变水泥石孔隙结构，提高密实度。

经研究选用的三峡二期围堰柔性材料的施工配合比见表1。

表1 三峡工程二期围堰柔性材料的配比Table 1 Proportion of flexible materials for the stage II cofferdam of the Three Gorges Project

对柔性材料的时间因素影响也在试验室进行了初步研究。成果表明，以28 d强度为基准，90 d的强度为28 d的1.5～2倍，1年的为2.5～3倍，2年的为5倍。以强度和模量而论，若28 d的抗压强度为2 MPa，E=200～300 MPa，数年后强度可达4～9 MPa，而E=1 000 MPa。由此看出，随时间延续，材料的性能不仅没有弱化，反而趋向优化。因此，这种材料可用于永久工程。

上述研究和施工经历了好几年的历程，在这过程中，3项工作的意义特别值得再提及：

（1）配方优化中的均匀设计

均匀设计是只考虑试验点在试验范围内均匀散布的一种试验方法，它的数学原理是数论中的一致分布理论。与正交设计相比可大幅度降低试验工作量。只需做10组试验，即可获得最优配合比，等价于正交设计的L 100（103）。这种方法是中科院数学所新的研究成果，在工程界应用尚不久，今后值得推广。

（2）力学参数与原材料关系的神经网络ANN模型

上述得到的最优配比是根据满足一定的力学特性要求而确定的，由于现场原材料的条件常有变化，如3种主要原材料水泥、风化砂、黏土中，除水泥特性比较固定外，其他2种都易变化，于是力学性质也可能随之变化。为了施工中随时了解力学性质是否能够满足，需建立原材料与力学性质的定量关系。而人工神经网络ANN技术具有很强的非线性映射能力，它本身是一个模型，很适合于多因变量、多自变量统计中的建模。根据建立的ANN模型，可预测出满足力学性质要求的柔性材料配合比。为了简化，将模型的预测数据降维，如先固定比较稳定的水泥用量，由ANN模型很快计算出不同风化砂和黏土含量，这种柔性材料的强度和模强比是能满足力学指标的。根据每一个水泥用量可绘制一个配合比图谱，并在图谱中标出合乎力学指标要求的配合比范围。使用表明，它对施工现场的控制十分方便和适用。

（3）柔性材料特性的时效问题

风化砂柔性材料具有良好的初期力学性能，施工方便、就地取材、经济性特好、环境效益尤佳、还易于拆除，确是一种好材料。但以往从未用过，而且其中含有大量易风化的颗粒，其性能会否随时间而衰化？运用5年后性能将如何？而且还有一个问题，就是防渗墙施工期前后持续很长，近300 d，若这期间材料性能变化很大，会否导致整个墙体的性状很不均匀，从而影响全墙的应力应变状况？这个问题虽在研制阶段做过室内的研究，表明其模量与强度均将增大。但最终结论还是在运用5年后，围堰拆除时的实地取样检验得出的，实测表明[5]，强度和模量都会随时间而增大，但强度比模量增加稍快，故模强比反而略有减小。渗透系数可降低3～4倍。如左漫滩段柔性材料抗压强度均值为7.23 MPa，初始切线模量均值为1 692 MPa，模强比均值为234；而右漫滩段的相应值各为5.93 MPa、1 467 MPa和247；右预进占段的相应值为4.29 MPa、797 MPa和186。可见，运用5年后，材料的性能不仅不会衰化，且更趋优化。

三峡二期围堰柔性材料的研制和成功应用是一件很有意义的事，它不仅可以在水利工程的防渗墙中应用，而且在基坑工程的地连墙、防渗墙中也有用武之地。