盾构下穿对既有地铁隧道沉降变形的影响研究
2023-01-13朱建才王蔡祥李新伟孙雅珍宋金龙
朱建才,王蔡祥,李新伟,孙雅珍,宋金龙
(1. 浙江大学建筑设计研究院有限公司,浙江 杭州 310027;2. 沈阳建筑大学 交通工程学院,辽宁 沈阳 110168;3. 中铁隧道股份有限公司,河南 郑州 450001)
0 引 言
在盾构施工下穿既有地铁隧道时,土体损失率C会影响既有隧道的沉降量,解决问题的关键在于正确得到土体损失率C及其与既有隧道沉降量间的关系。目前,国内外许多学者利用理论研究、数值计算、模型试验和实测分析的方法在盾构穿越对既有地铁隧道影响方面取得了一定的研究成果。魏新江等[1]对盾构穿越既有地铁隧道影响研究的现状进行了总结与展望;张琼方等[2-3]研究了盾构机与已建地铁隧道相对位置关系不同时,已建隧道的沉降变化规律;李倩倩等[4]通过地表沉降监测及盾构隧道变形监测等数据,研究了地层与既有结构的变形特性并分析了新建隧道与既有结构间的相互作用。陈越峰等[5]通过数值模拟,剖析了盾构下穿施工中变形沉降的变化规律及相应的施工影响,并与实测数据进行了对比分析,其结果可为施工方案设计提供依据。
不少学者选择工程研究的手段对此类盾构近接下穿既有结构的工程进行了研究。首先对于新建隧道引起的土层变化研究有:石杰红等[6]通过计算和数值模拟结果对比,认为修正 Peck公式及数值模拟法均可用于计算隧道开挖引起的竖向位移;宫志群等[7]通过室内模型试验并结合数值模拟得到了隧道开挖过程中洞周土体和地表土体的变形规律;HUANG等[8]进行了盾构隧道纵向模型试验,探究了盾构隧道下穿不均匀下卧层时纵向沉降的影响因素;YANG等[9]对软硬土层的隧道开挖进行数值模拟以研究其破坏模式。其次对于新建隧道穿越既有建筑(例如隧道等)的研究有:仇文革[10]通过研究重叠隧道建设、地铁区间邻桩施工、车站邻近基坑施工等典型邻近既有结构施工工程,阐明隧道近接施工及其影响预测的力学原理;王明年等[11]和章慧健等[12]模拟了盾构掘进施工,认为重叠隧道及隧道邻近建筑物施工的近接影响分区;LIN等[13]通过数值模拟研究了新建双洞斜穿既有隧道的变形特性,并研究了新隧道和既有隧道之间的交角对既有隧道变形沉降的影响;魏纲等[14]采用转动错台模型预测盾构穿越引起的既有盾构隧道纵向变形,并选取工程实例进行预测准确性验证;张晓慧等[15]根据盾构隧道近接下穿双层地下空间结构施工的模拟结果,研究了不同顶推力下盾构施工引起的沉降和附加内力的变化规律。隧道正交下穿施工扰动的情况下,既有上卧盾构隧道管片与接头处应力集中明显,局部裂损风险高[16]。上述研究虽然为实际施工提供了一些技术参考,但在盾构下穿既有地铁隧道的施工中,由于地质条件、现场施工技术的差异,仍需根据工程实际情况进行施工风险分析。
本文以杭州某工程盾构下穿地铁2号线项目为依托,采用非线性土体本构-小应变土体硬化模型(HSS模型),通过现场实测数据结合PLAXIS 3D软件进行参数反分析确定土体损失率C,为盾构下穿地铁2号线进行数值模拟提供符合实际的参数,分析施工过程中可能存在的风险,为下穿盾构施工提供技术参考。
1 工程概况及地质条件
1.1 快速路下穿地铁2号线段设计概况
本工程采用泥水平衡式盾构,刀盘直径为13.46 m,盾构隧道管片外径13.00 m,内径11.90 m,壁厚0.55 m,环宽2.00 m。隧道管片每环由10块组成,楔形量50 mm(双面),错缝拼装的通用衬砌环。衬砌环由1个封顶块(F),2块邻接块(L1、L2)及7块标准块(B1~B7)组成,如图1所示。接缝连接包括20颗环向连接螺栓(M36)和28颗纵向连接螺栓(M36)。管片混凝土强度等级为C50,抗渗等级P12。
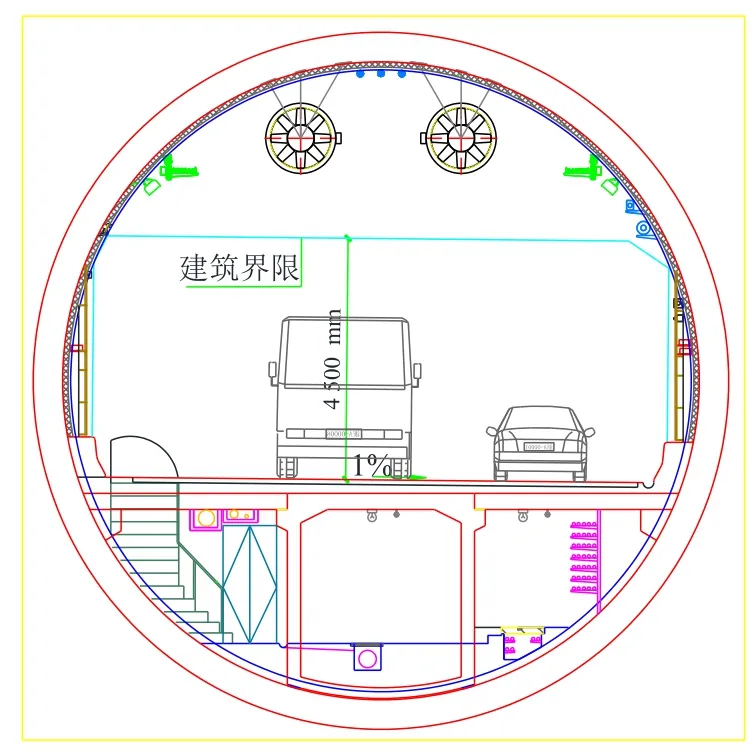
图1 快速路隧道剖面示意图Fig. 1 Schematic of shield tunnel
内部结构采用预制及现浇施工,主要包含烟道板、行车道板、防撞侧石、混凝土侧墙、预制口字件等内容。其中箱涵口字件、烟道板采用预制现场拼装施工,其余构件现场现浇施工。
1.2 快速路与地铁2号线的关系
南北线隧道在对应里程下穿地铁2号线如图2所示。
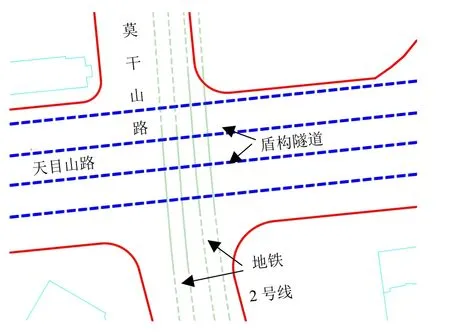
图2 快速路南北线盾构隧道与地铁2号线平面关系图Fig. 2 Relationship between shield tunnel of expressway north-south line and Metro Line 2
北线隧道顶距地铁 2号线左右线净距如图 3所示。
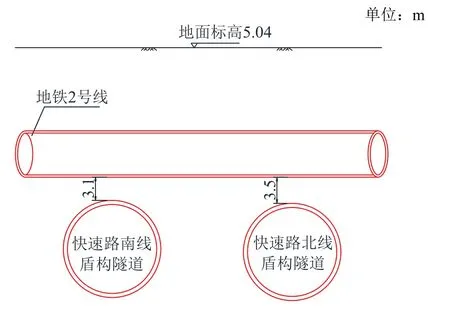
图3 快速路横断面与地铁2号线关系图Fig. 3 Relationship between the expressway cross-section and Metro Line 2
1.3 地质条件
根据下穿地铁2号线区域的勘察报告,快速路隧道覆土厚度约21 m,地铁2号线隧道覆土厚度约11 m。北线隧道断面范围主要为⑥1淤泥质黏土、⑥2黏土、⑦1粉质黏土、⑨1含砂粉质黏土、⑨2砾砂、⑩1黏土。南线隧道断面范围主要为⑥1淤泥质黏土、⑥2黏土、⑦1粉质黏土、⑳1全风化晶屑玻屑凝灰岩、⑳2强风化晶屑玻屑凝灰岩。隧道断面基本为上软下硬的复合地层。
1.4 土体损失率与反分析
根据Peck提出横向地面沉降估算公式为:
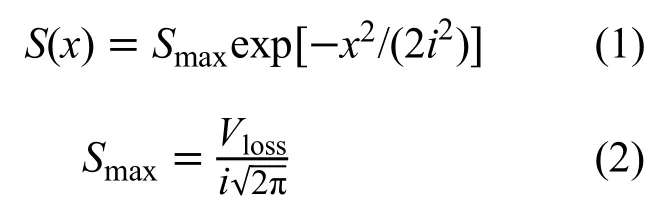
式中:x为距隧道轴线横向水平距离;S(x)为x位置处的地面沉降量;Smax为隧道轴线上方最大地面沉降量;Vloss为单位长度土体损失量,Vloss=πR2C,C为土体损失率;i为地面沉降槽宽度系数,i=kh,k为地面沉降槽宽度参数,h为隧道轴线埋深。
反分析通过有限元模拟设置多种不同的土体损失率C的工况,将有限元的地表横纵向沉降结果与实测值进行对比分析,选出与实测值最接近的土体损失率C的工况,并用于后续相同土体条件下的沉降变形预测分析。
1.5 MJS加固设置
地铁隧道加固桩共4排,共计50根,其中快速路北线17根,南线33根,加固深度为:快速路隧道顶至地铁隧道顶约9.7 m;其中地铁2号线隧道底以下采用直径为3.0 m的全圆加固对2号线隧道托底,控制隧道沉降;地铁隧道高度范围采用半圆180°摆喷加固,MJS桩中心距离地铁隧道外边线控制在 1 m,桩中心间距为 2.4 m,全圆加固咬合0.6 m(根据现场管线情况调整)。加固材料:P.O 42.5级散装水泥。其中地铁加固剖面图如图4所示;平面图如图5所示。
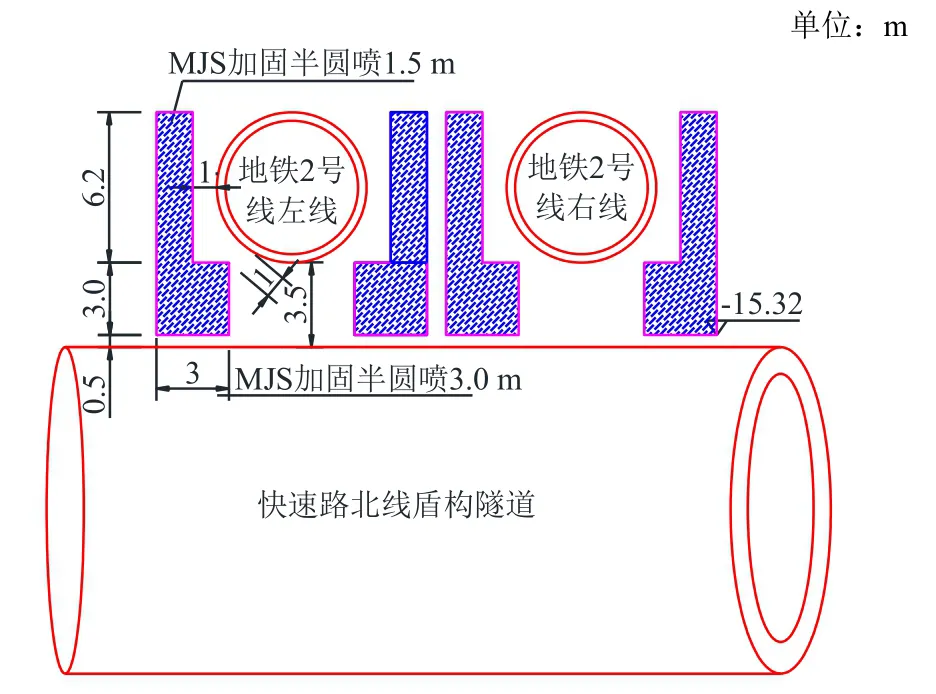
图4 地铁加固剖面图Fig. 4 Sectional view of metro reinforcement

图5 地铁加固平面图Fig. 5 Plan of metro reinforcement
2 小应变土体硬化模型(HSS)
HSS本构模型考虑了土体的剪切硬化和压缩硬化的特性与土在小应变时的刚度非线性变化的特征,土体刚度呈S型曲线衰减[17];与理想弹塑性模型不同的是,硬化塑性模型的屈服面在主应力空间中随塑性应变的发生而不断扩张,并非固定不变。土体硬化模型是一个可以模拟包括软土和硬土在内的不同类型的土体模型。
考虑相应的塑性应变,源于剪切硬化屈服函数的形式如下:

除了塑性应变外,该模型还考虑了弹性应变。塑性应变仅在初始加载中产生,而弹性应变在初始加载和卸载、再加载中同时产生。对于 σ2=σ3=常数的三轴排水试验应力路径,弹性杨氏模量Eur保持不变,则弹性应变由下式给出:
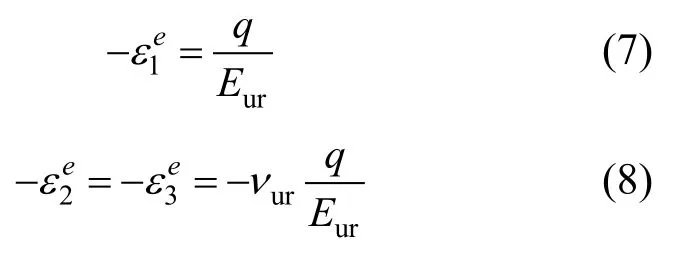
式中:νur是卸载和再加载阶段的泊松比。
3 数值计算与结果分析
3.1 参数反分析-土体损失率C的确定
为了确保大直径盾构下穿地铁2号线施工过程中地铁2号线的安全,在盾构下穿施工前通过有限元数值计算结合现场实测数据的方法预测盾构下穿对既有地铁2号线的影响。对北线已建NK3+890~NK3+730段建立三维数值模型结合实测沉降数据,通过参数反分析得到盾构模拟参数,以便为后续盾构下穿地铁2号线的数值模拟提供一定的依据。
以盾构隧道纵向为X轴,盾构隧道横向为Y轴,竖向为Z轴建立三维有限元模型,其中为了消除边界条件的影响,模型尺寸取 160 m×200 m×86 m(X·Y·Z),模型网格采用空间四面体10节点单元划分,共82 833个单元,119 734个节点。有限元整体模型如图6所示。边界条件为土体底部施加x、y、z方向的约束,土体沿z方向的两侧施加z方向的约束,土体沿x方向的两侧施加沿x方向的约束。计算过程严格按照实际施工步序来模拟,本次对施工过程的数值模拟将划分为 86个工况,如表 1所示。
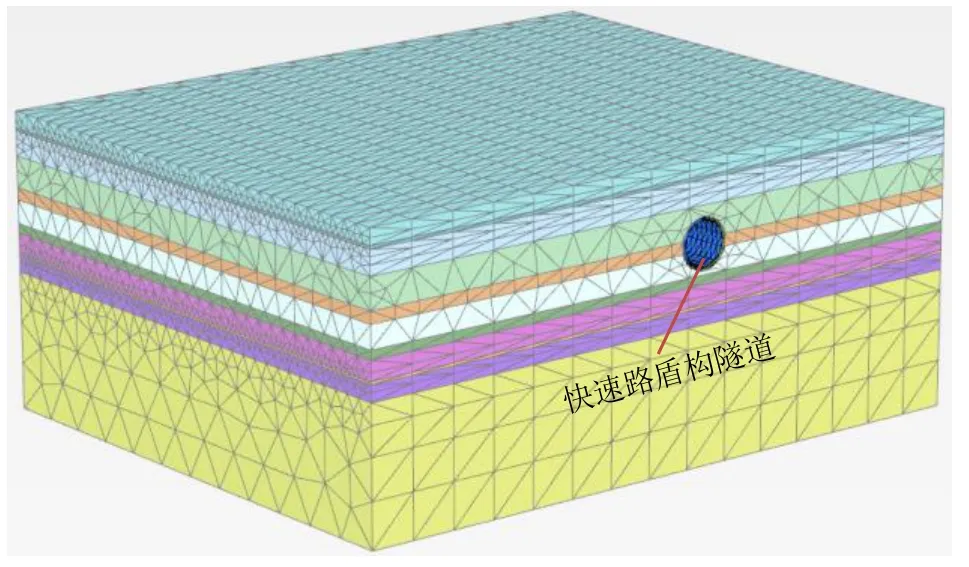
图6 北线已建NK3+890~NK3+730段盾构隧道有限元模型Fig. 6 Finite element model of section NK3+890~NK3+730 of the north line
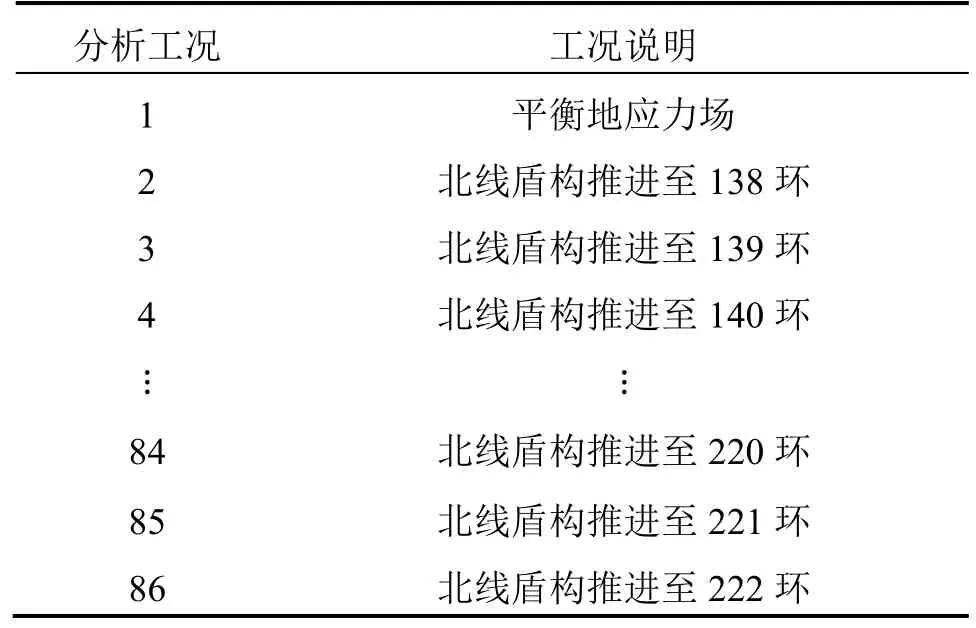
表1 北线已建NK3+890~NK3+730段盾构隧道分析工况Table 1 Working conditions of section NK3+890~NK3+730 of the north line
在NK3+890~NK3+730段计算模型的基础上,通过调整模型土体损失率C进行参数敏感性分析,并将模拟结果与实测地表横纵向沉降值进行对比,从而确定最接近的土体损失率C,并为后续的分析提供基础。反分析中土体损失率C依次取0.05%、0.09%、0.10%、0.15%和0.20%,并通过在Plaxis 3D中盾构机开挖推进时的Cref来设置实现。
计算完毕后,提取不同土体损失率C情况下北线盾构顶推至第179环时的模型竖向位移云图如图7所示。从图中可以看到,随着土体损失率C的增大,模型沉降变形不断增大。当土体损失率C>0.15%时,最大沉降将大于10 mm。
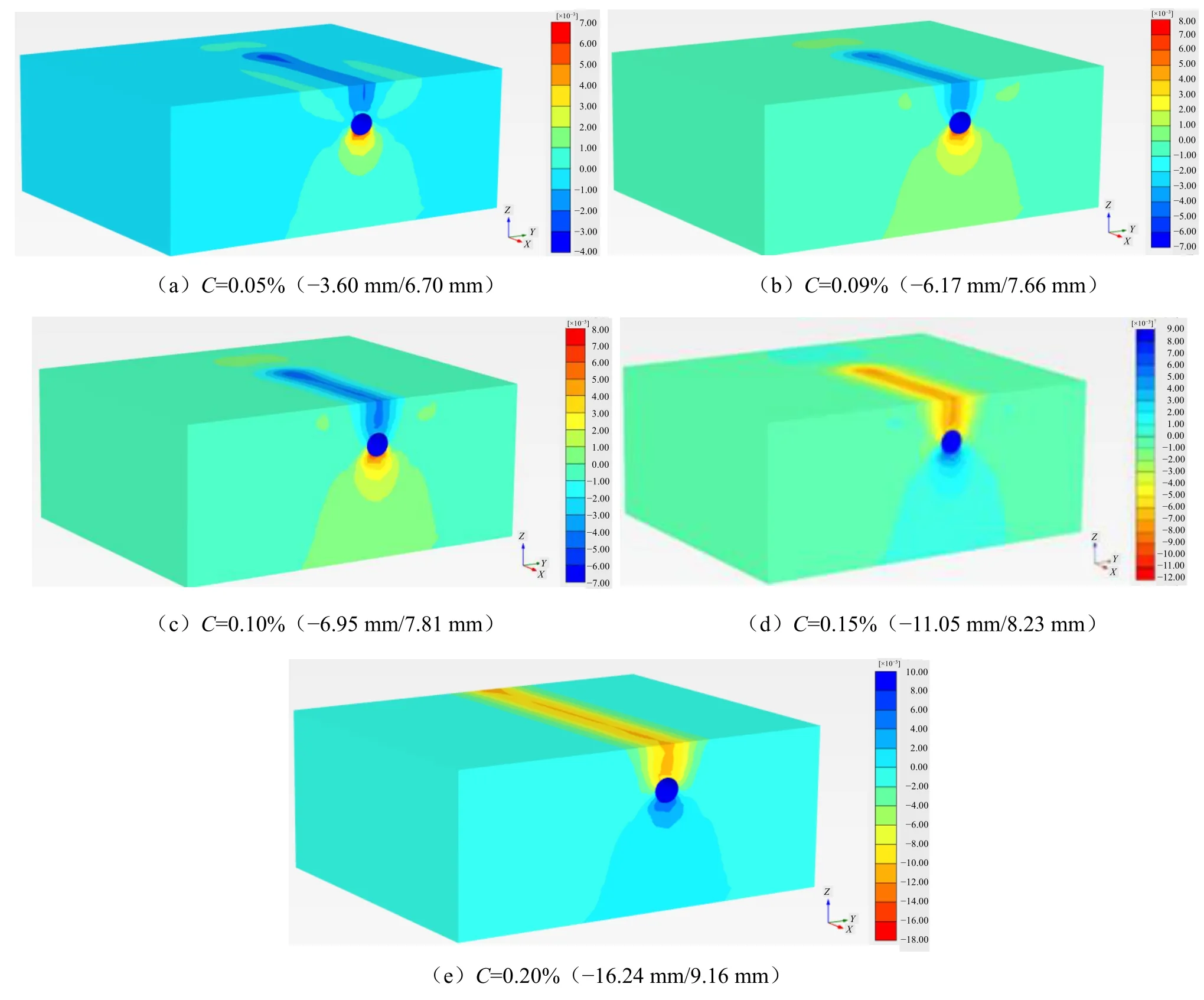
图7 模型竖向位移云图Fig. 7 Cloud map of vertical displacement
根据空间几何位置关系,确定实际监测点在有限元模型中的相应位置,提取对应测点位置沿隧道纵向和横向分布的地表沉降数据,并将不同土体损失率C情况下的地表沉降数据与实测数据绘制成曲线图,如图8所示。由图可知,随着土体损失率C的增大,地表横向沉降及纵向沉降均不断增大;地表横向沉降在盾构隧道中轴线位置出现最大值,并向两侧逐渐减小;地表纵向沉降最大值出现在盾构机对应范围内;盾构机所在范围内地表沉降变化不大;盾尾后方地表沉降随着与盾构机距离的增大略有所减小;掌子面前方地表沉降随着与盾构机距离的增大而不断减小。图中数据显示,当土体损失率C=0.09%~0.10%时,计算值与实测值较为接近,因此后续可采用该土体损失率C对盾构下穿地铁2号线进行分析以预测盾构施工对地铁2号线的影响。
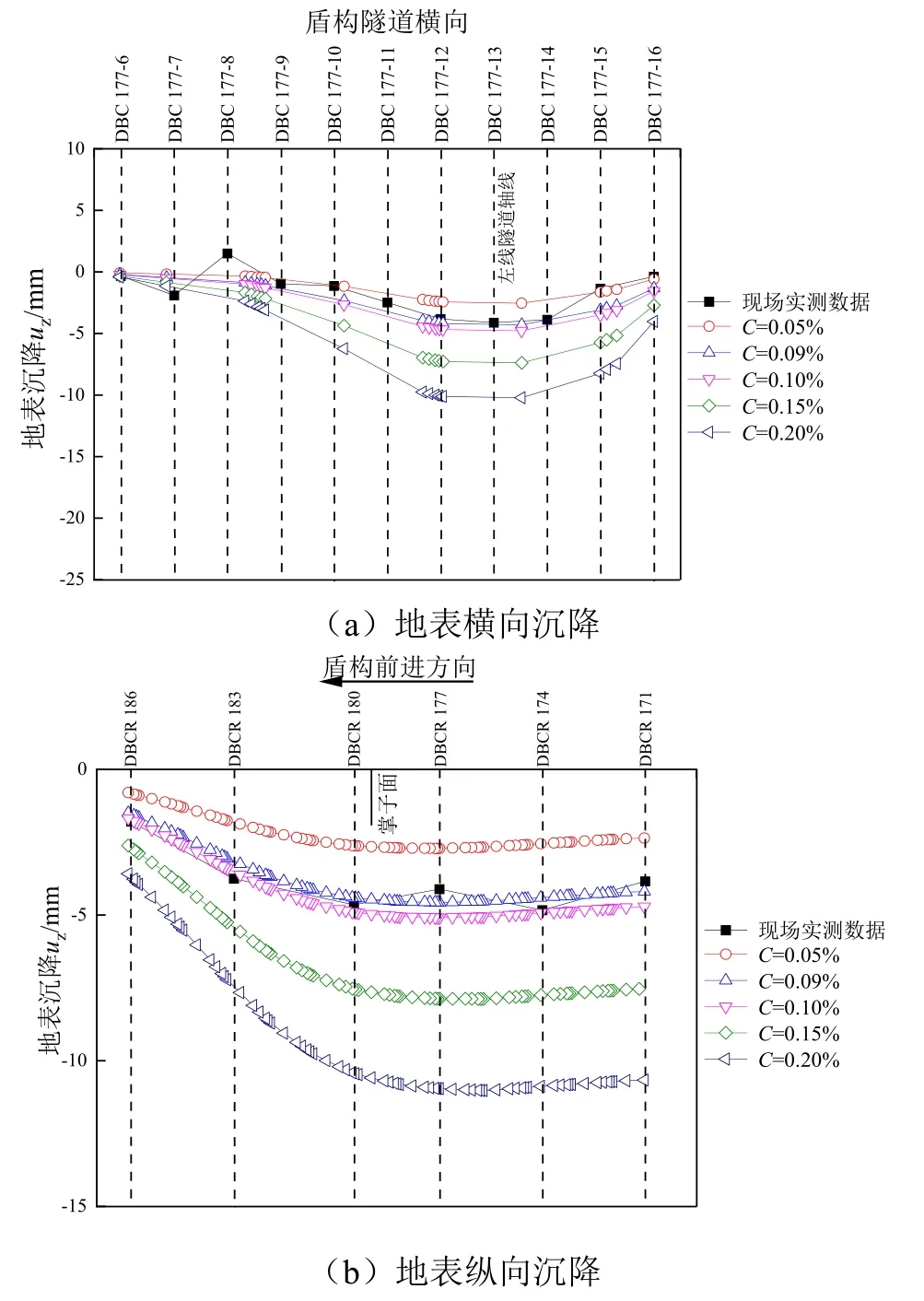
图8 地表沉降计算值与实测值对比Fig. 8 Comparison of calculated and measured values of surface settlement
3.2 盾构下穿地铁2号线数值建模
(1)盾构下穿地铁2号线计算模型
根据地铁控制保护区范围对盾构下穿地铁2号线段进行建模分析,考虑盾构南、北线第345~403环管片顶推施工先模拟北线盾构施工,待北线穿过地铁控制保护区后,再模拟南线盾构施工。盾构下穿地铁 2号线计算模型同样以盾构隧道纵向为X轴,盾构隧道横向为Y轴,竖向为Z轴建立三维有限元模型,其中为了消除边界条件的影响,计算模型尺寸取118 m×200 m×86 m(X·Y·Z),模型网格采用空间四面体10节点单元划分,模型共149 761个单元,217 871个节点。有限元整体模型如图9所示,地铁、盾构隧道以及MJS加固模型如图10所示。计算过程严格按照实际施工步序来模拟,本次对施工过程的数值模拟将划分为130个工况,如表2所示。
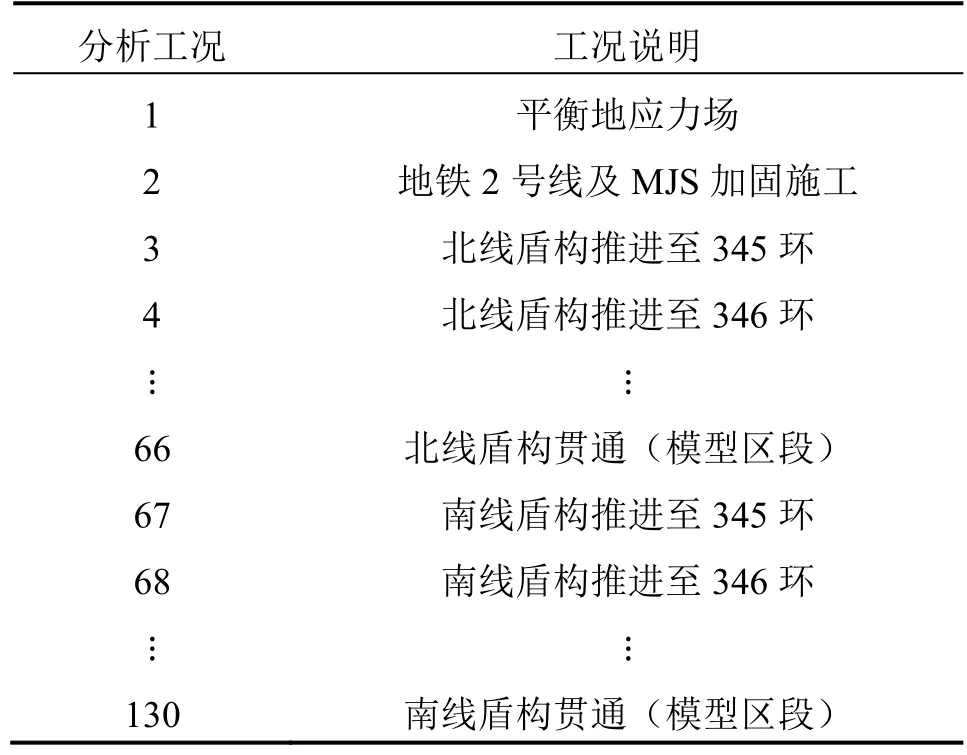
表2 快速路盾构隧道下穿既有地铁2号线运行隧道分析工况Table 2 Working conditions of expressway shield tunnel through existing running tunnel Metro Line 2
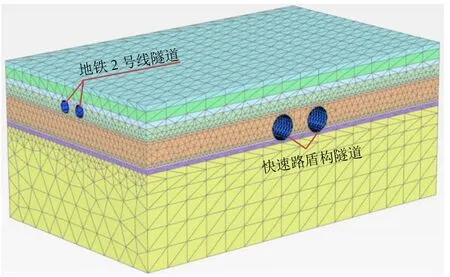
图9 快速路盾构隧道下穿既有地铁2号线运行隧道有限元整体模型Fig. 9 Finite element model of expressway shield tunnel through existing running tunnel Metro Line 2

图10 地铁、盾构隧道以及MJS加固有限元模型Fig. 10 Finite element model of subway, shield tunnel and MJS reinforcement
(2)结构尺寸与土体参数
隧道与盾构器械结构尺寸参数如表3所示;已建地铁2号线隧道管片参数如表4所示;土体HHS参数如表5所示。

表3 结构尺寸参数Table 3 Structure size parameters m

表4 地铁2号线隧道管片参数Table 4 Parameters of tunnel segments of Metro Line 2
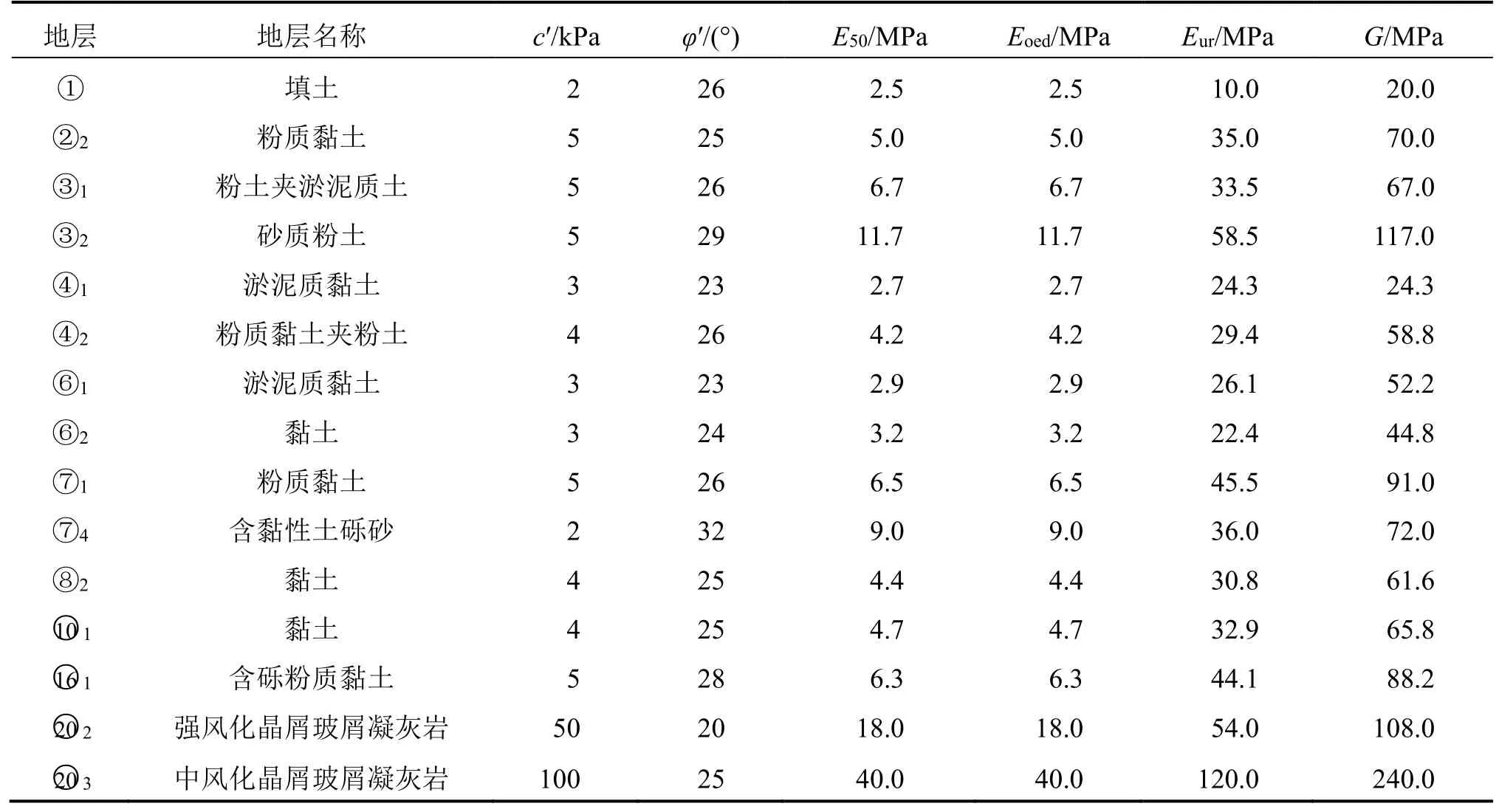
表5 HSS土体本构模型参数表Table 5 Constitutive parameters of HSS model
(3)盾构开挖模拟步骤
PLAXIS 3D模拟盾构隧道掘进过程如下:
a)进行地应力平衡。
b)模拟盾构机进入,每一环向掌子面施加 盾构支护力,防止地表发生沉降变形。
c)“冻结”土体以此来模拟土体开挖,随后“激活”盾构机单元,最后在掌子面上施加支护压力。
d)“激活”对应位置的衬砌和同步注浆单元,设置注浆压力模拟注浆过程来释放多余应力,最后“冻结”上一步中激活的盾构机单元。
e)重复步骤c)和d),直至开挖完毕,盾构机出土后移除注浆压力模拟注浆体固结。
3.3 盾构下穿地铁2号线模拟结果分析
根据 NK3+890~NK3+730段参数反分析得到的土体损失率C=0.10%对相同土体条件下的盾构下穿地铁2号线进行数值模拟,分析盾构下穿对地铁2号线的影响。
图 11为下穿施工过程中不同工序下的地铁隧道沉降变形云图,从图中可以看到,随着盾构的不断推进,地铁隧道沉降不断增大,其中沉降主要发生在盾构机顶推至地铁隧道下方过程中,而当盾构机通过后,地铁隧道后续所产生的沉降相对较小。南北线盾构施工分先后顺序,在北线盾构隧道贯穿后,南线盾构开始施工,当南线隧道下穿地铁2号线时,由于对地铁2号线产生两次影响,地铁隧道沉降进一步增大。其中369环为盾构刚到达既有2号线右线的位置,在此位置进行南北线盾构施工时的沉降数据,主要监测南北线施工先后顺序的两次影响。本次地铁隧道总体沉降均较小,与现有规范[18]相比较,满足了地铁变形控制的要求。
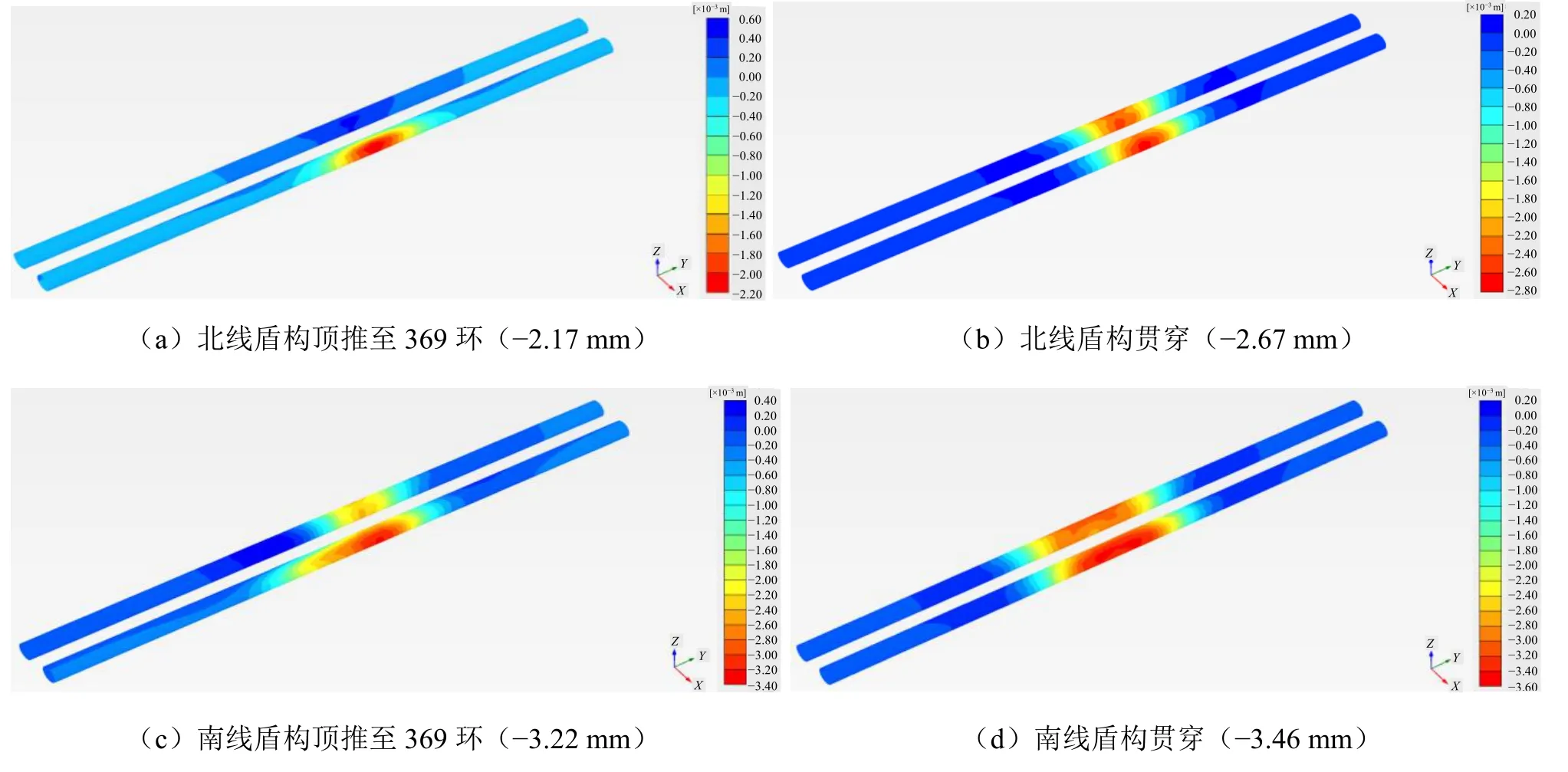
图11 盾构隧道沉降变形云图Fig. 11 Settlement deformation contours of shield tunnel
3.4 MJS加固效果分析
本工程中采用MJS对地铁 2号线进行了预先加固。为了探究MJS在盾构下穿过程中对地铁隧道变形的控制作用,采用有限元数值模拟的方法对比分析了无加固情况下及采用 MJS加固情况下盾构下穿对地铁2号线沉降变形的影响。
图12与图13分别为采用MJS加固和无加固情况下地铁隧道沉降变形云图和双线地铁隧道中间剖面竖向变形云图。
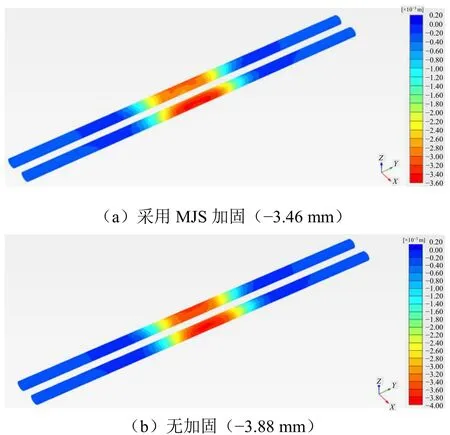
图12 盾构隧道沉降变形云图Fig. 12 Settlement deformation contours of shield tunnel
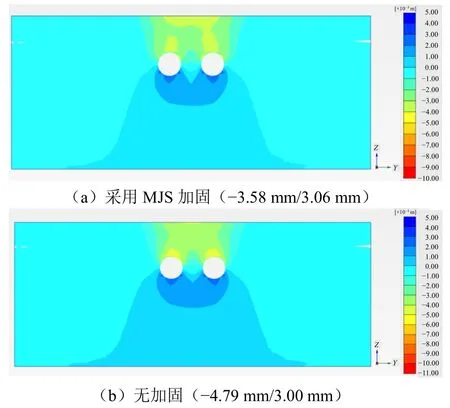
图13 双线地铁隧道中间剖面竖向变形云图Fig. 13 Vertical deformation contours of the middle section of double-track Metro Line 2
由图可知,采用MJS加固后,地铁隧道沉降变形由无加固时的-3.88 mm减小到了-3.46 mm,即MJS加固在一定程度上减小了地铁隧道的沉降变形,起到了控制作用,但从数值上分析,沉降量仅减小了0.42 mm,换算成控制效率仅为10.8%,控制效率较为一般。MJS加固对控制双线地铁隧道中间剖面土体沉降变形效果较好,控制效率达到了25.3%。
3.5 多工况对比分析
在有限元数值模拟中,土体损失率的取值与盾构施工过程中各方面因素均有关。有限元数值模拟结果显示土体损失率的取值与盾构施工过程中各方面因素均有关。
通过对北线 NK3+890~NK3+730段的多工况反分析所得到土体损失率C结果显示,该工程在此段盾构施工质量较好,土体损失率C仅为 0.10%左右。若后续下穿地铁2号线施工质量能够保证,可按该土体损失率C进行有限元预测,若后续施工过程中受部分施工因素影响,导致土体损失率C有所提高,则需在适当提高土体损失率C取值的前提下进行有限元预测。考虑到后续施工过程中可能受部分施工因素影响,导致土体损失率C有所提高,因此研究中通过适当提高土体损失率C的取值展开了进一步分析。图14为地铁隧道沉降变形云图。
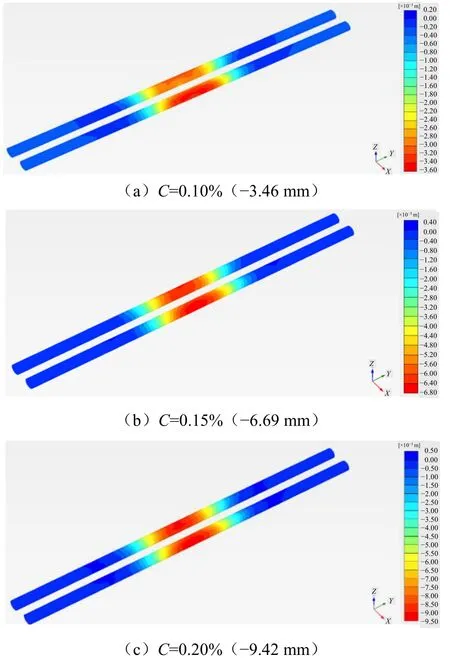
图14 地铁隧道沉降变形云图Fig. 14 Settlementand deformation cloud map of Metro Line 2
图15为不同土体损失率C时地铁隧道沉降变形云图。由图可知,随着土体损失率C提高,地铁隧道沉降变形逐渐增大。根据土体损失率C与地铁沉降关系图显示,当C=0.10%~0.20%范围内,地铁沉降与土体损失率C为近似的线性关系。
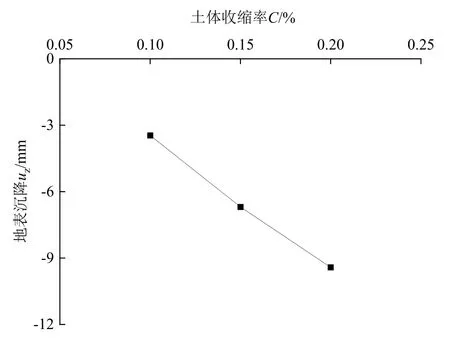
图15 土体损失率C与地铁沉降关系Fig. 15 Relationship between soil loss rate C and subway settlement
4 结 论
本文对杭州某盾构隧道工程下穿地铁2号线施工数值计算预测分析,以完工的 NK3+890~NK3+730段为依据,对该段建立三维有限元计算模型,在此基础上结合实测数据进行参数反分析,得到盾构施工模拟参数——土体损失率C,进而对盾构下穿地铁2号线进行数值计算预测分析。通过本次计算,主要得到以下结论:
(1)NK3+890~NK3+730段的多工况分析结果显示,盾构在该区段施工时所对应的土体损失率C约为0.10%。
(2)采用NK3+890~NK3+730段参数反分析得到的土体损失率C对盾构下穿地铁2号线进行数值模拟发现,地铁隧道总体沉降变形较小,满足地铁变形控制要求;地铁隧道沉降主要发生在盾构机顶推至地铁隧道下方过程中,而当盾构机通过后,地铁隧道后续所产生的沉降相对较小。
(3)采用有限元的方法对MJS加固效果进行分析发现,MJS对地铁隧道沉降变形具有一定的控制效果,但控制效率仅为10.8%左右;MJS对控制双线地铁隧道中间剖面土体沉降变形效果较好,控制效率达到了25.3%。
(4)基于盾构下穿地铁2号线计算模型对土体损失率C进行多工况分析发现,当C=0.10%~0.20%时,地铁沉降与土体损失率C为近似的线性关系。
