U-系统与V-系统的理论及应用综述

陈 伟，蔡占川，李 坚，梁延研，熊刚强，宋瑞霞

U-系统与V-系统的理论及应用综述

陈 伟1，蔡占川2，李 坚3，梁延研2，熊刚强4，宋瑞霞5

(1. 江南大学人工智能与计算机学院，江苏 无锡 214122； 2. 澳门科技大学计算机科学与工程学院，澳门 999078； 3. 澳门理工大学应用科学学院，澳门 999078； 4. 广东医科大学信息工程学院，广东 东莞 523808； 5. 北方工业大学理学院，北京 100144)

传统的Fourier 级数在逼近间断信号时因 Gibbs现象的干扰，会产生比较大的误差。针对此问题，国内学者齐东旭教授带领的课题组提出了非连续正交函数系的研究课题，其中U-系统和V-系统是两类典型的非连续完备正交函数系。从数学理论上来说，U-系统和V-系统分别是对著名的Walsh函数和Haar函数由分段常数向分段次多项式进行推广的结果，其最重要的特点是函数系中既有光滑函数又有各个层次的间断函数。因此，U，V-系统可以处理连续和间断并存的信息，在一定程度上弥补了Fourier 分析和连续小波的缺憾。本文从理论与应用2个方面对U，V-系统进行了综述。在理论方面，首先介绍了单变量U-系统与V-系统各自的构造方法，其次介绍三角域上U，V-系统的构造方法，最后介绍U，V-系统的主要性质。在应用方面，介绍了若干具有代表性的应用案例。

U-系统；V-系统；正交函数；非连续；频谱分析

熟知，用有限项Fourier级数表达间断信号时，在间断点处会出现波动，且这种波动不能因求和项数增大而彻底消失，即著名的Gibbs现象。Wilbraham于1848年首先观察到这一现象，之后Gibbs (1839—1903年)做了深入细致地研究。Gibbs现象的研究之所以引起关注，在于其出现造成了数据偏差。在数字图像、语音处理，以及用Fourier方法求解微分方程等问题中，人们需设法消减其影响[1-2]。

在几何信息处理问题中，Gibbs现象的影响更应引起重视。因为在二维及三维几何造型中，几何对象往往包含许多部件和零件。作为几何图组，其子图相互分离(强间断)以及非光滑连接(弱间断)的情况不可避免。几何造型的精度要求很高，如果说信号处理的某些问题中Gibbs现象的出现尚可接受，那么在几何信息表达中则是不可容忍的。

众所周知，在图像、语音等信号处理中，正交函数理论是频谱分析与综合的数学基础，由此发展出一系列强有力的实用算法，有利于生成或提取对象的特征，从而在分类，乃至识别问题里得到应用。正交函数与正交变换在数字信号处理领域的成功应用，有必要扩大到几何信息特别是几何造型的领域。将频谱分析方法引入几何造型，首先是正交重构问题，其关键是采用什么样的正交函数才能避免Gibbs现象。具有好的连续性的正交函数，在此反而派不上用场。于是，研究既能用于通常的信号处理问题，又能适应几何图组整体表达与分析需要的非连续正交函数，无论是理论还是实用，都是十分重要的[3]。

非连续正交函数的研究，兴起于20世纪初期。历史上，为了回答“是否存在非连续的完备正交函数系”的问题，美国数学家WALSH[4]构造了后人称之为Walsh函数(1923年)，初衷仅作为数学上的“反例”。然而，到了70年代，随着半导体技术与大规模集成电路的出现，此类仅取值1或–1的二值函数，显示了独特的功效，在信号处理领域一度掀起Walsh函数的研究热潮。

比Walsh函数出现得更早些，1910年匈牙利数学家HAAR[5]提出了称之为Haar函数的完备正交函数系。若不考虑规范系数，Haar函数则仅取值1，–1或0。其中强调Walsh函数与Haar函数的等价性，给出了相互线性表示的关系，但是Haar函数具有更加简洁的结构。几十年后，当小波兴起之后，人们发现Haar函数恰是最简单、最基本的小波，从而使得Haar函数在小波分析中占有重要地位。

Walsh函数和Haar函数是非连续正交函数的典型代表，其均是分段零次多项式。从函数逼近角度，其收敛速度不高。而在实际问题中，信号往往既包含渐变(光滑)部分，又包含突变(间断)部分，而只具有强间断性的函数很难实现信号的自适应表达。

U-系统和V-系统，完整的名称应该叫“次U-系统[6]和次V-系统[7]”，是由一系列次分段多项式组成的2[0, 1]上的2个正交完备函数系，犹如姊妹篇，特点是函数系中既有光滑函数又有各个层次的间断函数。U，V-系统可以处理连续和间断并存的信息，在一定程度上弥补了Fourier分析和连续小波的缺憾。

特别值得注意的是，当=0时，U-系统就是Walsh函数，V-系统则是Haar函数，因此U，V-系统分别是Walsh函数和Haar函数的自然推广。将一个0次函数系推广到次函数系，无疑是极具数学意义的。Walsh函数和Haar函数分别创建于1923年和1910年，而U，V-系统分别建立于1983年和2007年，Walsh函数推广到U-系统历时60年，而Haar函数推广到V-系统则历时近百年。

这里需要说明一下U，V-系统与小波的关系。小波分析是调和分析的重大发展，在小波分析的发展史上，最早可以追溯到1910年Haar构造的一组完备规范正交基(即Haar函数)，不过当时还没有“小波”这个概念。一个公认的事实是，1984年法国工程师让·莫莱特(Jean Morlet)在分析地震波的局部性质时，发现传统的Fourier变换难以达到要求，因此其首次引入小波分析这一概念，用于地震数据的收集与分解中。随后其与物理学家亚历克斯格罗斯曼(Alex Grossmann)将该研究工作发表在学术期刊上，从而拉开了小波分析研究的序幕[8]。

U-系统的基础理论研究由国内学者齐东旭教授与冯玉瑜教授在1980—1982年在美国Wisconsin (Madson)大学数学研究中心(MRC)访问期间合作完成，并于1981年首次在MRC公开报告[9-10]，回国后随即于1983年在国内中国科学技术大学学报上公开发表学术论文[11-12]。虽然U-系统不是严格意义上的小波，但是U-系统中已经出现了小波的“基因”，且离小波仅“一步之遥”。因此，当小波出现后，美国IBM公司的MICCHELLI和北达科他州立大学的XU[13]明确指出，U-系统是一类“预小波(prewavelet)”。而V-系统出现后，文献[14]已从数学理论上证明了，V-系统是一类严格的有限区间上的多小波基。

在U-系统研究的初期，齐东旭教授将U-系统作为参与中国早期计算几何协作组的专题，从1983年开始在吉林大学招收硕士研究生，接着在中山大学、中科院列入培养博士研究生计划，同时在特区澳门科技大学招收博士研究生。继而U-系统的研究获得国家自然科学基金的资助。本世纪初，齐东旭教授团队在U-系统的基础上提出了V-系统，在保留U-系统几乎全部优点的基础上，更具有小波特性，从而在理论及应用上获得更加满意的结果。在连续十余年间，相关学者做出许多新推进，得到多项国家自然科学基金资助。作为阶段性总结，本文将从理论和应用方面对U，V-系统进行综述。

1 U-系统与V-系统理论

1.1 单变量U-系统与V-系统的构造

单变量U-系统是齐东旭教授和冯玉瑜教授于上世纪80年代初的研究成果，而单变量V-系统是齐东旭教授带领学生们在2007年的研究成果。

U-系统的构造继承了Walsh函数的思想，采用的是“压缩与正、反复制”的方法，只是初始函数不同；V-系统的构造则是在U-系统的基础上，继承了Haar函数系的思想构造得到的。次U，V-系统均由分段次多项式构成，也都是2[0,1]上的完备正交系。

次U-系统的构造步骤：

步骤1.取区间[0,1]上的前+1个Legendre多项式，作为次U-系统的前+1个函数(即第一组函数)，记为0(),1(),···,l()，这是熟知的函数，有具体表达式。

步骤2.求出+1个分段次多项式，称之为生成元{f(),=0,1,···,}(生成元满足的条件见下文)，得到第二组函数。

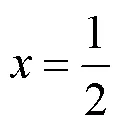
再由新生成的函数组经过“压缩、复制与反复制”，依次递归无限进行下去，得到的无限个函数构成的函数序列，即为次U-系统。

次V-系统的构造步骤：

步骤1和步骤2.同上述U-系统的过程完全一样。

步骤3.压缩并局部复制生成后续序列，将{f(),=0,1,···,}中每个函数按照下面的方式压缩复制为

因此得到次V-系统，也是由可数无穷多个函数构成的函数系。(注：上述所有函数在间断点处，可定义函数取值为左右极限的平均值)。

次U，V-系统均是从Legendre多项式出发，再构造+1个生成元，U-系统是通过对这些生成元的“压缩、复制与反复制”所得到，V-系统则是通过“压缩、局部复制”所得到。无论是U-系统还是V-系统，起核心作用的是共同的“生成元”，为了保证函数系的正交完备性，+1个生成元f(),=0,1,···,必须满足以下条件：

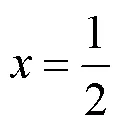
按照生成元的条件，可以用待定系数法通过求解非线性方程组而得到。=0～3次的生成元有直接表达式，见文献[3]。

文献[15]从另一个角度研究了U，V-系统生成元(文献[15]称为小波函数)的构造，从Legendre 多项式和截断单项式出发，通过Gram-Schmidt 正交化过程，得到生成元的数学通项表达，同时证明了生成元的存在性。

另一方面，次V-系统也可以经过次U-系统的线性组合得到。首先，完全相同的步骤1和步骤2，说明其前2(+1)个函数完全相同；其次，V-系统的步骤3得到每个函数，可以经过U-系统步骤)得到的某2个函数“相加或相减再除2”得到，见文献[3]。因此次U-系统和次V-系统从代数关系上说是等价的。

V-系统还有很多等价的构造方法，如从Franklin函数出发，从截断单项式出发，经过Gram-Schmidt正交化方法得到V-系统，见文献[3]。

U，V-系统最突出的特点是函数系中的间断信息，与物理学及工程技术领域的间断、跳跃、突变等紧密相关，因此可用于这些“异类”信号的处理问题。

=0,1,2,3次U，V-系统的前若干个函数的图形见图1。

1.2 U、V变换及其快速算法

对离散信号进行U，V-系统分析，必须用到有限U，V变换。在实际应用中，一般需要构造离散U-系统或离散V-系统的正交矩阵。以离散U矩阵为例，将区间[0,1]等分为=2个子区间，在每个子区间上分别对前个基函数0(),1(),···,U-1()作积分，得到=2个向量，形成矩阵

一般说来，矩阵并不是正交的，需要再经正交化得到相应的正交U矩阵或正交V矩阵。有了正交矩阵，就可以对离散信号进行U，V正交变换与分析。

可以看出，通过上述方法实现的U，V变换，需要事先计算并保存某一固定阶数的变换矩阵，当信号的长度很大时，计算效率将变得很低。

图1 U-系统和V-系统部分函数图((a) k=0～3次U-系统部分函数；(b) k=0～3次V-系统部分函数)

关于次离散U变换的研究，文献[16]给出了更一般的阐述，特别对2次离散U变换，建立了矩阵表示的递推关系与快速算法，具体给出了4点、8点、16点矩阵的快速算法流程图。并利用Kronecher积，推导出正交U变换的直接分解算法。

而对于快速离散V变换，有2种算法给予实现[3]。一种是间接方法，先对信号进行快速U变换，再经Hadamard矩阵变换得到V变换结果；另一种是直接运用V-系统多小波的特性，得到相应的小波分解与重建算法，即Mallat算法，此不赘述。

1.3 三角域上U-系统与V-系统的构造

从一维情形向二维或更高维情形的推广，简单而直接的形式是张量积，将正交函数用于图像处理问题，普遍用到张量积形式。但对几何信息处理、特别是计算机辅助曲面造型问题，除了张量积形式，更有三角域形式要研究，因为三角面片在几何造型中具有简便灵活的优点，三角域上的曲面造型已经得到非常广泛地应用。

研究三角域上次U，V-系统的定义[17-18]，一个重要目的在于实现曲面造型的正交重构，从而能将频谱分析方法引入几何设计。

1988年齐东旭教授得到了三角域上的Walsh 函数和Haar函数的具体表达，2008年又率领弟子们得到了三角域上的U，V-系统的表达，且有直角坐标和面积坐标2种表达形式。

由于三角域上的表达较复杂，限于篇幅，仅给出构造的大概思想，具体细节参考文献[3]。

三角域上的次U，V-系统也是分组构造的：

第(≥3)组：对第二组中的生成元进行4-2倍压缩，然后在三角域4-1剖分子区域上，U-系统按照“复制和反复制”生成后续函数列，V-系统则按照“局部复制”生成后续函数列，此过程中为了保证函数列的规范性，需要配置恰当的规范系数。至此得到完整的三角域上次U，V-系统。

图2给出了三角域上V-系统的构造示意图。

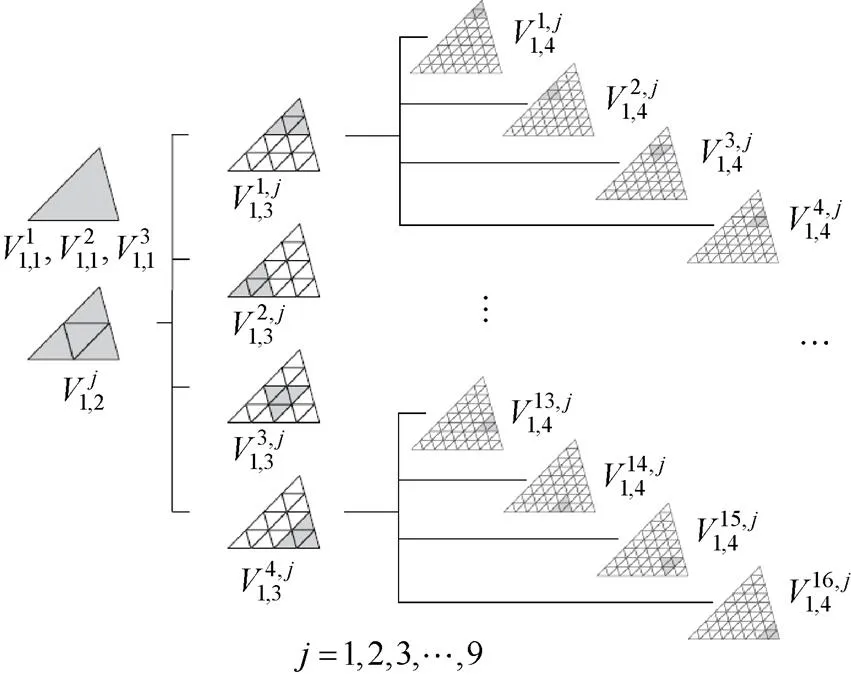
图2 三角域上V-系统的构造示意图

1.4 主要性质

作为2类关系十分紧密的完备正交函数系，U-系统与V-系统既具有相同的性质，也具有各自不同的特征。本文将列出一些主要的性质，具体证明可参考文献[3]。

性质1.完备正交性。

任意次U-系统和次V-系统都是2[0, 1]上的完备正交函数系。

性质2.级数收敛性。

记{1(),2(),···,(),···}为次U-系统或次V-系统基函数，给定函数，相应的Fourier-U级数或Fourier-V级数为

则有

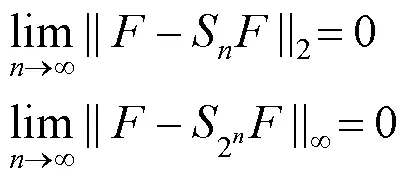
其中，SF为式(4)右端的部分和，即

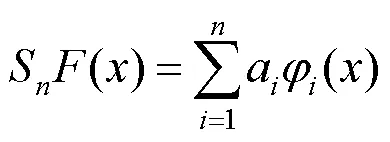
性质3.级数再生性。

性质4.U-系统序率性。

当从0到1增大，U-系统函数值符号的改变次数呈递增规律。

性质5.离散1次U-系统是斜变换。

斜变换在信号处理中有广泛的应用价值，且有快速算法。因此U-系统也可以看作是斜变换的推广。

性质6. U-系统是一类有限区间上的预小波。

性质7. V-系统是一类有限区间上的正交多小波。

V-系统中第一组函数，即前+1个Legendre多项式，就是多小波的尺度函数；第二组即+1个生成元函数就是小波函数。

小波分析是上世纪80年代末发展起来的调和分析方法，并在信号与图像处理的众多领域中得到了广泛地应用。多小波是在单小波研究基础上提出的概念，早期的单小波，是由一个尺度函数生成的小波。单小波不可能同时具备对称性、有限支集、正交及二阶消失矩等性质，但是多小波却可以同时具备这些性质。因为V-系统的多小波特性使得V-系统的应用更为广泛。

2 U-系统与V-系统的应用举例

U，V-系统是Walsh函数和Haar函数向高次情形的推广，在间断点处具有各个层次的间断：从-1阶导数、-2阶导数，···，直到函数本身间断。正是由于U，V-系统中的函数出现各个层次的间断，使其在表达用分段多项式描述的几何对象时，用有限项的Fourier-U，V级数可以精确重构原来的几何模型。

国内学者在U，V-系统的理论和应用方面做了许多探索[19-58]，本文仅摘录几类典型例子。

2.1 几何模型的精确重构与频谱分析[19-27]

几何信息处理与图像信息处理的数学技术有很大差别。前者的研究，大体归为计算几何学(代表性的数学工具诸如样条插值与拟合、Bernstein- Bezier方法、子分割算法等数值逼近理论，及计算复杂性理论)；后者归为数字图像处理技术(代表性的数学工具有各种正交变换：Fourier，Walsh，Hadamard，Slant和Wavelet等)。以Fourier及小波分析为代表的变换理论，无论在理论上还是广泛地应用方面，在包括图像在内的信号处理方面，已经表明其是强有力的数学工具。然而，利用正交变换的频谱分析这一强有力手段，在几何信息的描述(如曲线、曲面的数学表达、几何图组的整体特征生成与提取)方面，却没有足够的表现与施展。简言之，关于曲线与曲面的数学，关注基函数(如Bernstein，B-样条，NURBS等)的研究，但不追求基函数的正交性，因而计算几何学的研究内容未包括频谱分析。

为什么现行的诸多正交函数(如Fourier函数系、小波等)未被用来表达曲线与曲面呢？其中Gibbs现象是主要障碍。由Fourier分析理论可知，在间断点出现的地方，Fourier级数的不一致收敛性质，使得有限的计算步骤不能避免Gibbs现象。U，V-系统的出现，使得频谱分析方法引入计算几何学，用U，V-系统表达几何对象时可以消除Gibbs现象，做到精确重构。

图3是V-系统对汽车模型(作为一个几何图形)的重构与Fourier重构效果的比较。显然V-系统128项就可以精确表达，而Fourier重构中即使用3 000项，Gibbs现象依然存在。

三角域上U，V-系统可将3D几何对象精确表达，图4是三维模型中很有代表性并经常被引用的Dragon模型，试验中使用的模型有871 414个三角面片。通过对三角面片的V-系统分解，得到，，3个方向的谱，就可以对模型精确重构。

图3 V-系统对几何图组的精确重构((a)汽车轮廓； (b) Fourier重构(100项)；(c) Fourier重构(500项)； (d) Fourier重构(1500项)；(e) Fourier重构(3000项)； (f) 3次V-系统重构(128项))

图4 Dragon模型及其3个方向的频谱 ((a) 3D几何模型；(b)频谱)

当把一个几何对象精确表达之后，就可以通过U，V-系统的正交性特点，从U，V-系统的谱系数中提取几何对象的特征，进而进行分类识别，这就是几何对象的频谱分析方法。

2.2 分形曲线生成[28-29]

通过上述介绍可知，给定一个几何对象(不论是单体的还是群组的)，U，V-系统可以实现对其的正交分解及精确重构。实际上，作为一类特殊的基函数，通过对U，V-系统的频谱系数进行改变，能够主动生成新的几何模型。以分形为例，在分形的生成问题中，一般是通过对某个初始几何对象的迭代操作来实现，经典的方法包括L系统、迭代函数系统(iterative function system，IFS)等。而在文献[28-29]中，首次提出了分形曲线生成的频谱方法，分别提出了基于V-系统和正交Franklin函数系的分形曲线生成算法。

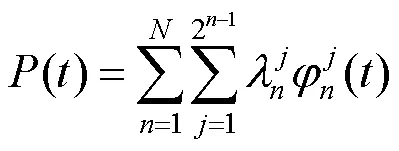
若将第层全部基函数记作向量形式

相应的频谱向量为

那么，

可以看出，上式给出了分形的一种新的表示方法，并使得分形的高低频分布层次更加分明，更好地刻画了分形的自相似结构。

为了对频谱系数进行修改，对每层的频谱向量引入一个调节参数α，=1,2,···,，得到

其中，()为对原分形频谱系数进行修改而生成的新的分形。因此，通过设置不同的参数向量，可以得到不同的重构曲线。图5给出一个从Hilbert曲线出发，通过改变V-系统参数，生成多种新的分形的例子。

2.3 2D形状检索和3D模型检索[30-43]

U，V-系统可以定义相应的描述子和矩，用于识别、分类以及检索。本文以V-系统为例(U-系统完全类似)，给出2D商标的特征描述。

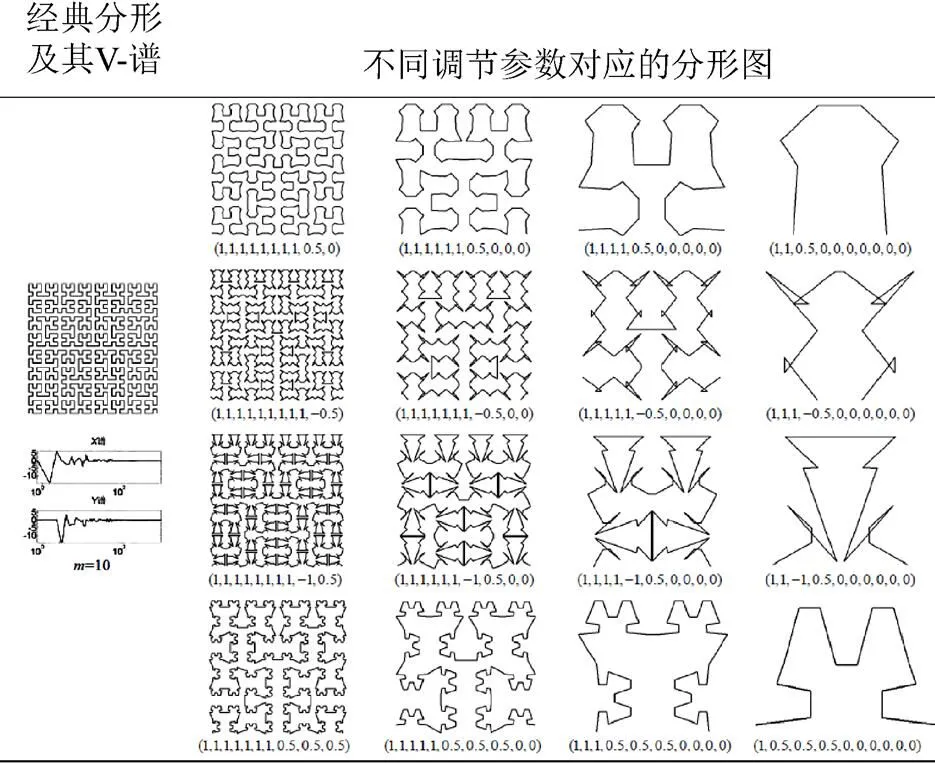
图5 基于V-系统频谱的分形曲线生成

对商标检索或几何对象分类，需先解释下面一些必需的概念。

(1) V-系统的离散化：即求一个2阶的离散V-矩阵，其过程是：取V-系统的前2个基函数，对第个基函数在[0，1]区间均匀地取2个值(也可以取函数在每个小区间上的平均值)，构成一个2阶方阵的第行，当=1,2,···,2，就构成一个2阶方阵；一般来说这个方阵还不是正交矩阵，对其正交化即得到离散正交V-矩阵。的取值由所处理的信号来决定。

(2) V-描述子：对图像或几何对象提取边界，得到边界点列{P(x,y)|=1,2,···,2}(可以采用插值方法使其边界点数为2)。对这个边界点列进行正交V-变换为

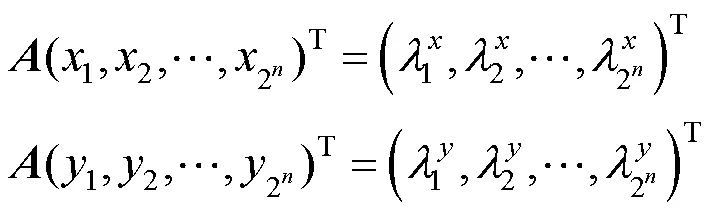
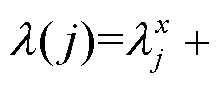
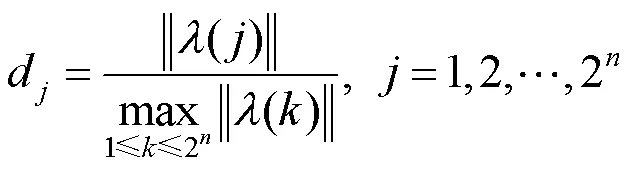
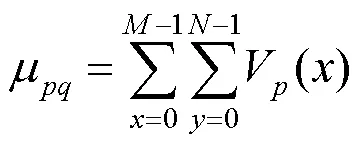
利用特征向量的欧氏距离可以度量2幅图像的差距，从而实现图像的分类和检索。检验算法的可靠性要在通用商标数据库中进行实验，V-描述子和V-矩在商标检索时取得了较好的实验结果。图6给出了一个检索例子。

图6 针对实验数据库中的商标检索比较实验

(4) 分层V-系统：文献[31]给出基于层次V系统的复杂商标表示方法，提出基于多阶次(=0,1,2,3)的V-系统生成的分层V-系统(HV系统)，层次结构带来了更详细的形状表示信息的同时，仍然保持了V系统本身在正交系统中的优势。同时还提出层级式V系统的正交化描述子(HV描述子)，证明了HV描述子满足旋转、平移和尺度变换的不变性。层次V-系统方法可以在避免产生Gibbs现象的同时，用合理的描述符、且较少的项数来表示复杂的商标，并能获得准确地表示结果。图7给出层次V系统的算法流程。

图7 层次V系统的算法流程图

(5) U，V旋转不变矩：旋转不变性在图像模式识别中具有基本的重要性，传统的以Zernike矩为代表的变换在模式识别、边缘检测、纹理分类、方向估计、图像重建等领域得到了广泛地应用。然而，传统矩方法均以多项式为核函数，存在表达式复杂、数值计算不稳定、特征提取能力弱等缺点。文献[33]将U系统与三角函数结合，构造了一类极坐标系下的二维旋转不变的数学变换。

记u()为次U系统中的第个基函数，定义单位圆盘上的U-调和基函数为

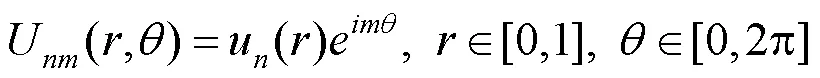
其中，=0,1,2,···；=0,±1,±2,···。可以看出，U-调和基函数由角向的三角函数和径向的U系统函数的乘积组成。

设定义在单位圆盘上的图像为(,)，其二维旋转不变U变换为

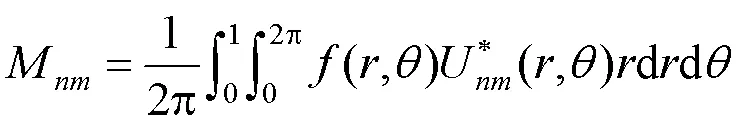
则图像(,)旋转前后，其二维旋转不变的U变换系数的模||M||不变。

除了旋转不变性以外，二维旋转不变的U变换还具有诸如多分辨率性、函数支撑均匀性、序率性、间断性以及数值计算简单等，这些性质在图像特征提取中均起着重要的作用，详细内容见文献[33]。

需要指出的是，虽然U系统是一类正交函数系，但式(14)定义的U-调和基函数不再满足正交性。一般说来，同时具备正交性、旋转不变性以及分段低次性是很困难的。在文献[34]中，通过对V系统基函数的改造，构造了一类正交旋转不变V变换。

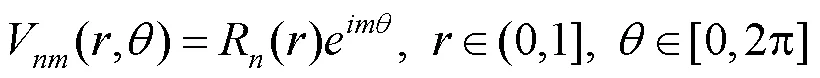
那么，需满足正交性要求，即

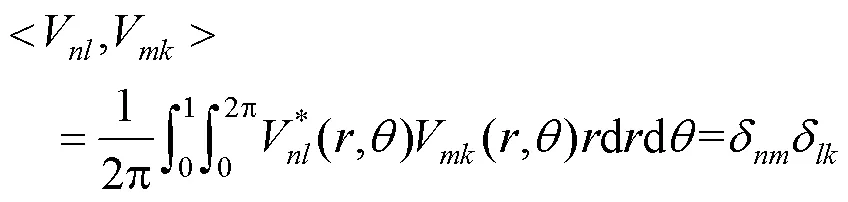
因此，可实现正交旋转不变V变换及正交重构。在实际计算过程中，由于在加权V-系统基函数在零点附近存在奇点，若直接计算会导致数值不稳定，文献[34]通过重采样技术得到极坐标系下等面积扇形像素(如图8(a)，(b)所示)，从而能够精确计算出积分结果。

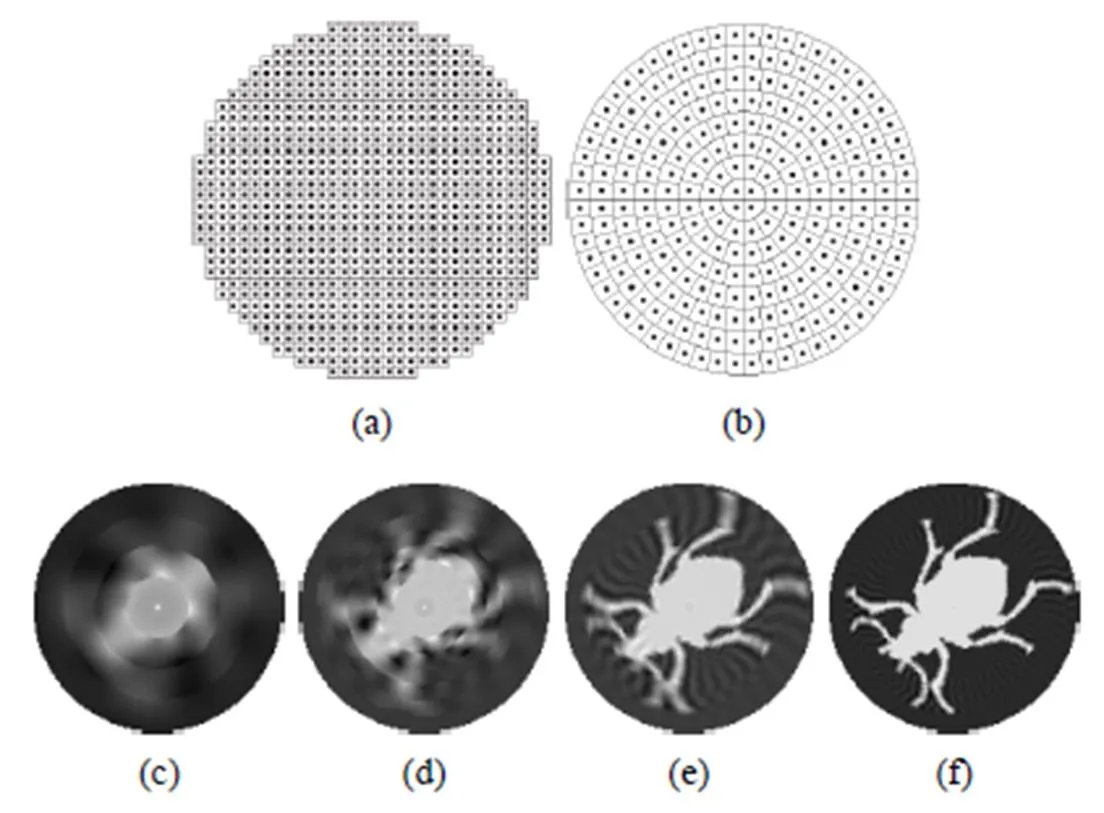
图8 正交旋转不变V变换中的重采样及正交重构((a)笛卡尔系下像素；(b)极坐标系下像素；(c)～(f)分别用8阶、16阶、32阶、64阶基函数进行图像正交重构)

基于正交旋转不变的V变换的图像重构如图8(c)所示。文献[34]将正交旋转不变的V变换应用于二值图像的检索，取得满意效果。

对3D几何模型的检索要用到三角域U，V-系统，首先要将几何模型参数化，将模型的三角网格映射到三角域(图9)，然后对参数化后的模型进行U，V-系统的分解，得到，，3个方向的谱系数。设模型(可以是群组)在U，V-系统下频域表达为

文献[32]基于V-系统提出V-Laplace描述子，用于3D模型检索，取得非常好的效果，图11是其中一个检索例子。

2.4 2D图像和3D模型的数字水印[44-46]

将一个信号(2D图像或3D几何模型)在U，V-系统之下分解后，得到谱系数，可以精确重构原信息。基于这个原理，可以实现数字水印的植入。具体植入水印的方法很多，最基本的是在谱系数的中频部分植入水印的谱系数。为了保证水印的鲁棒性，要设计高质量的植入技巧，使得水印可以抵抗各种攻击。

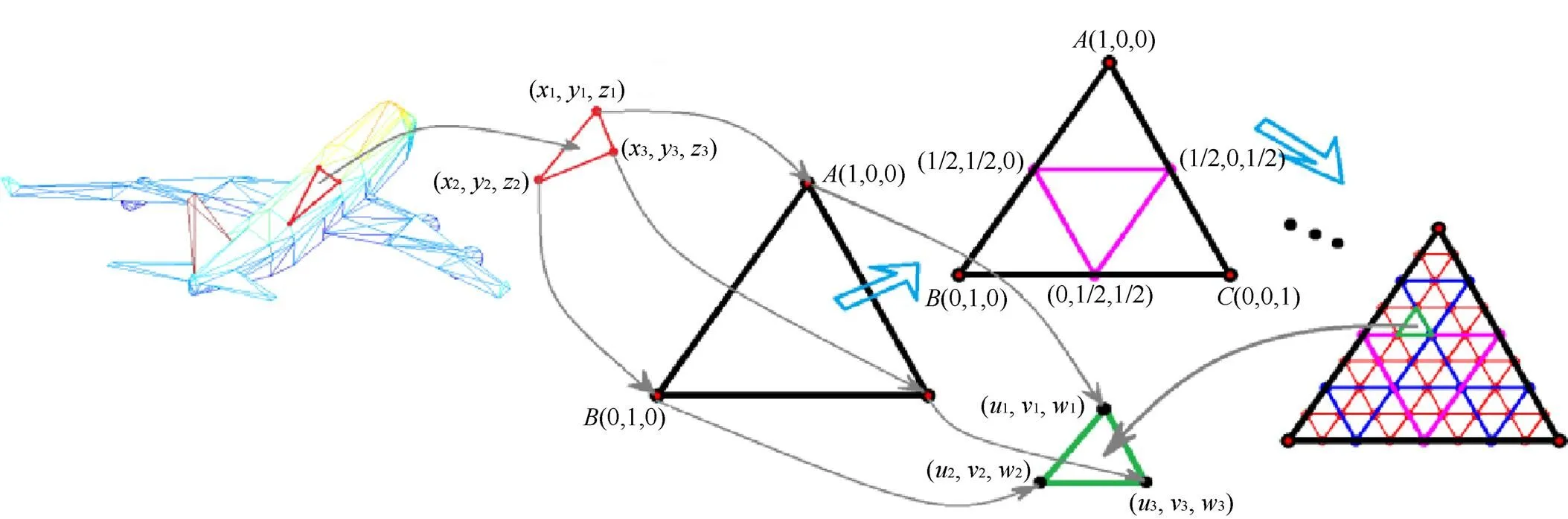
图9 三角网格模型参数化示意图

图10 3D模型群组检索的比较试验((a)本文方法；(b)几何矩方法；(c)剪影轮廓FV方法)

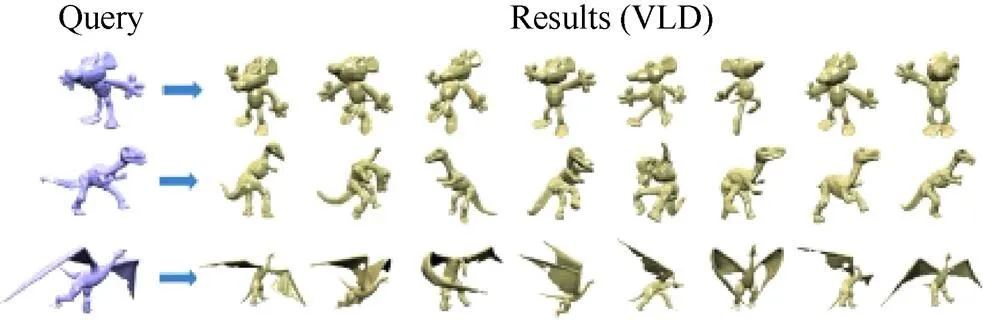
图11 V-Laplace描述子用于3D模型检索

图12所示是2D图像的数字水印例子，小图像“手”是水印。

3D模型水印的植入，首先要将3D模型参数化，然后在V-系统下展开，得到3个方向的谱系数，将水印的谱植入到模型的谱中，整个过程技巧很多。表1～3是一个3D模型水印植入和提取以及抗攻击的效果，其中的二值图像“中国梦”为水印。

图12 基于V-系统的数字水印植入及抗攻击实验

Tabel 1 Subjective and objective evaluation of the watermarked model and extracted watermark

表1 水印模型和提取水印的主观及客观评价

表2 噪声攻击实验结果

2.5 多尺度全月球粗糙度分析[47]

地形粗糙度是描述地理信息中地形复杂程度的重要参量。传统的粗糙度技术只将粗糙度当作是地形高低差异的统计参量，并未对粗糙度信息进行提取和分析。因此，现存的粗糙度可视化模型(图像、三维模型)并不能准确地显示出地形的粗糙度信息。通常对于地形粗糙度的研究更多是将粗糙度当作描述地形高程变化的参量，并未将粗糙度特征提取作为重心，更多只是在地形高程变化差值的基础上，改变统计量化的方式来描述地形粗糙度特征。基于高阶离散小波V-系统(2次，3次)能够使用非线性分段次多项式来表达几何信息的特点，提出了基于V-系统的地形特征提取因子的构造算法和提取后特征量化算法，用来反映不同尺度复杂地形地貌表面的起伏程度，解决传统大部分算法基于局部高低差进行量化，导致结果忽略密度高，地形起伏频度高，但高低变化不明显特征变化的问题。

表3 裁剪攻击实验结果

传统算法不仅无法将地形信息中的光滑部分去掉，还会丢失相当一部分的粗糙度信息。使用V-系统中的非连续函数可以更准确地将地形粗糙度特征从原始数据中提取出来。如图13所示，V-系统粗糙度技术不仅在可视化图像中能够显示出更多的粗糙度信息，且从统计结果上看(表4)，V-系统粗糙度地图对于细小的粗糙度信息的提取更加准确，0.0～0.1区间内，V-系统的特征点比传统技术更少，说明V-系统在这些被传统算法认为完全或者几乎是光滑的区域内识别到更多的粗糙度信息。

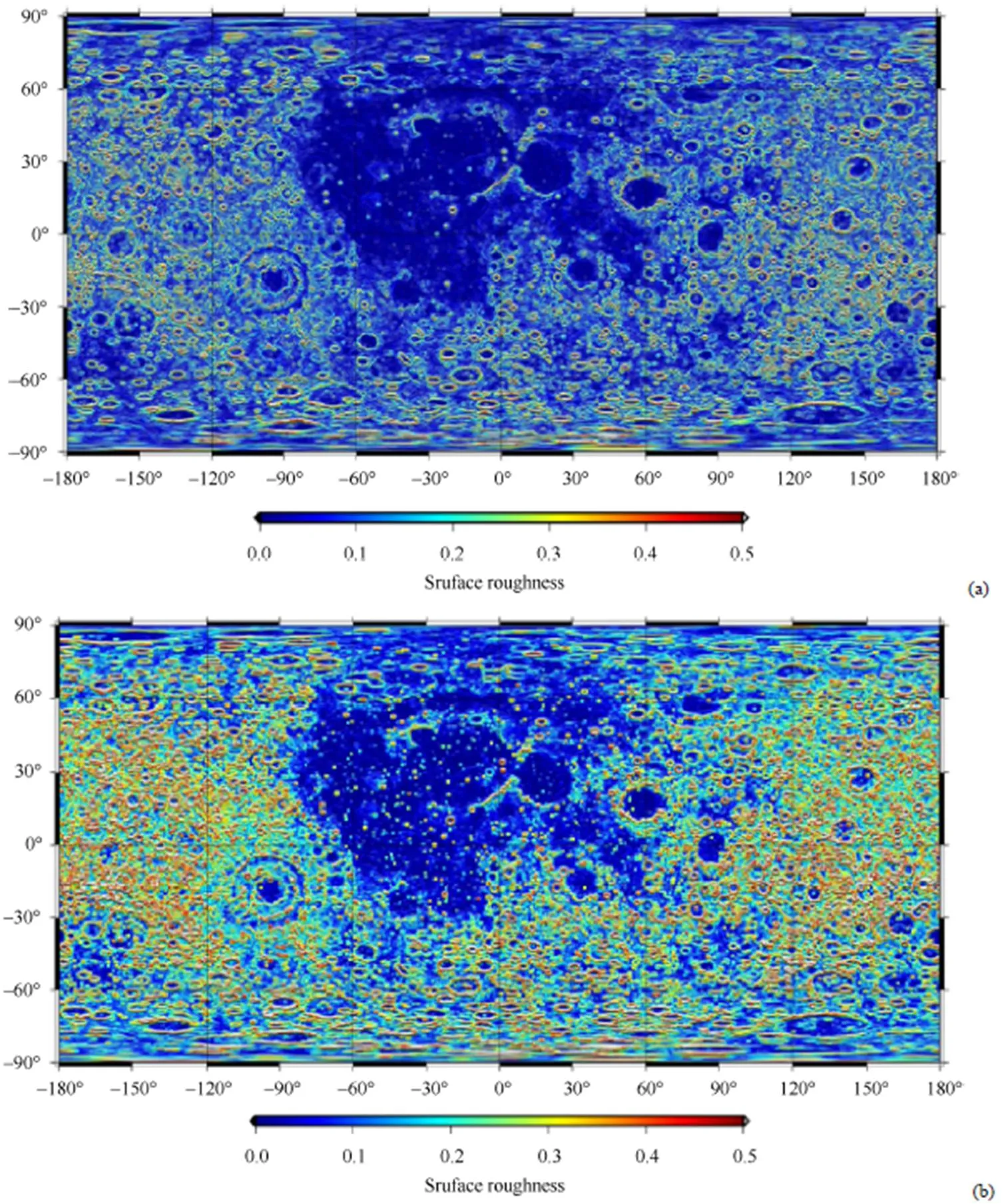
图13 基于V系统的月球地形地貌分析

2.6 数字图像处理[48-56]

U，V-系统在图像处理中的应用，与一般正交系原理相同，但V-系统因为是多小波，所以具备更多小波的功能。图14说明V-系统能有小波一样的分解，这样的性质使得V-系统在图像压缩、图像去噪、图像去雾、图像增强、图像融合中有特别的应用。图15～17所示为图像去雾、增强及融合的例子。

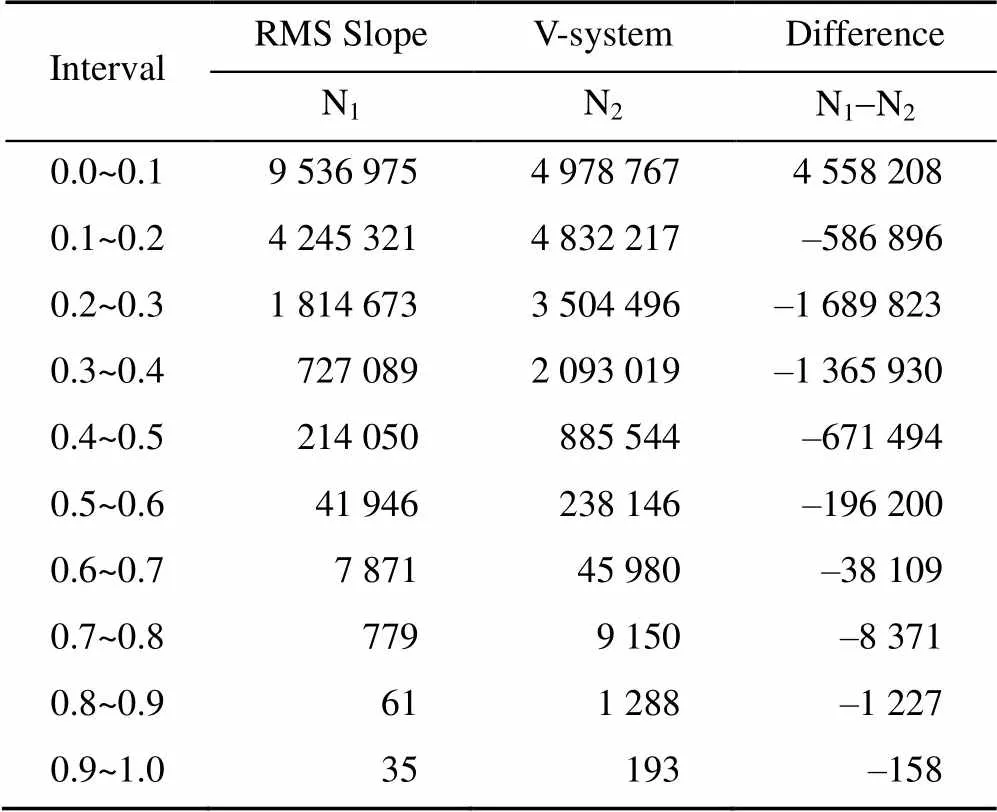
表4 月球地表粗糙度统计结果

图14 图像的三层V-系统分解

图15 图像去雾((a)雾图；(b)去雾图像)[52]

2.7 V-系统与神经网络结合[57]

文献[57]提出了一种基于V-变换与卷积相结合的图像超分辨率模型(图18)。新的模型主要由V-变换模块、特征融合模块和上采样模块组成。一张低分辨图像(low resolution image，LR)首先经过V-变换模块完成初级特征提取的任务，然后经过特征融合模块获取更丰富的信息，所有的信息输入到下采样模块中，将学习到的特征变为需要的大小，最终得到清晰的超分辨图像(super-resolution image，SR)。特征融合模块的位置可以被现存的任何卷积神经网络替代，只需要匹配接入网络的输入和输出通道大小。

图16 图像增强((a)低照度图像；(b)增强图像)[53]

图17 医学图像融合((a) CT图像；(b) MRI图像；(c)融合图像)[54]

图18 模型示意图

2.7.1 V-变换与卷积

V-变换需要经过两次矩阵乘法，因为矩阵乘法的计算方式，使得运算对于正交V-矩阵和LR图像的大小有很大的限制，且必须保持一致。因此带来了计算力和时间的消耗，而且一旦的大小发生变化，一个固定大小的矩阵在大小上不能与之匹配，网络的训练就会出错，对于V-变换的使用变得死板。文献[55]通过将矩阵乘法转化为卷积点乘的方式解决该问题，用2×2矩阵示意，即

2.7.2 V-变换模块

图19为V-变换模块。一张输入图像分别经过V-变换、卷积层和激活层之后，将过程中产生的所有信息都相加输入到后续网络中。以往的超分辨卷积神经网络模型，无论是否与小波变换相结合，网络结构多么复杂，模型深度如何，在网络特征提取的初期都会使用一个3×3的卷积，直接将网络的通道数增加到64，这样直接且简单地处理不能很好地完成早期的特征提取任务，后续深度卷积神经网络的表达能力会受到限制，造成网络效果不好。

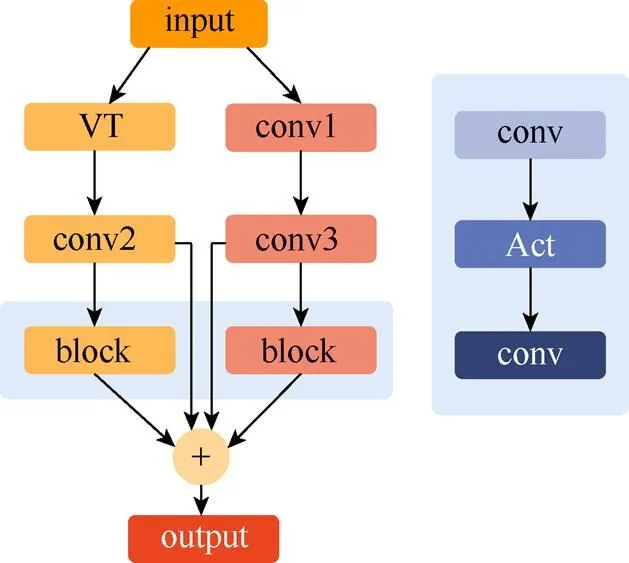
图19 V-变换模块示意图

V-变换能更好地在特征提取的初期提取频次信息，丰富的信息可以促进卷积神经网络的表达能力。首先利用V-变换作为过渡，将网络通道数缓慢地增加到64，既可以提取到更多超分辨任务关注的频次信息也可以细致地捕捉更多细节；其次，V-变换与普通卷积并行，也就是空域与频域并行，将所有捕获的特征都输入到后续的卷积神经网络中，为后续的训练提供丰富的特征。

2.7.3 V-损失函数

本文提出新损失函数的理论基础是，无论在空域还是频域，超分辨图像(SR)和高分辨图像(high-resolution image，HR)损失函数的值达到最小时，预测结果最准确。V-损失为

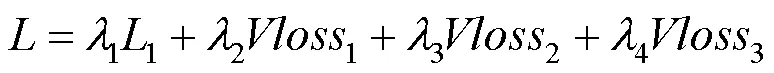
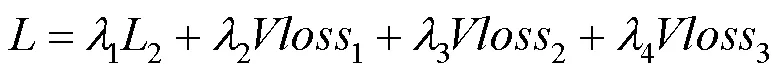
采用两阶段的训练方法。将式(19)作为主损失函数，先对网络进行一轮训练，充分利用L1损失函数保留信息的能力和V-损失对于高频信息在重建中的引导作用，训练得出的参数对于超分辨任务已经有了很好地预测作用。第二阶段的训练，用(2.5)对已经训练好的参数进行提纯，进一步提升网络预测能力。无论第一阶段的训练还是第二阶段的训练，都是在频域上进行，因此两阶段的训练都有V-损失函数的出现。

只是一个简单的训练手段，未添加任何新的模块，两阶段法可以提升PSNR值，这样低成本的提升方式是人们一直寻找的。

上述方法在图像超分辨率重构任务中有出色的表现，在通用数据集上的实验结果表明，与当前很多优秀的算法相比，无论是定性还是定量标准，都具有更好的实验结果，见文献[57]。

2.8 V-系统用于新冠肺炎评估[58]

数字图像特征识别技术的研究具有重要的意义，诸如生物工程、医疗诊断、机械行业等。为了开展基于胸部CT图像的新冠肺炎感染区分割、检测和诊断研究，文献[58]提出了一种基于V系统的从胸部CT影像中识别肺部感染特征新方法，并根据选取的影像特征评估COVID-19肺部感染的严重性(图20)。首先在胸部CT影像中，针对双肺的分割，校正确定肺部区域，并获得肺轮廓；然后，选取粗糙度、对比度、粗略度和熵作为感染区域纹理特征以获取COVID-19感染区域，以及病变轮廓；最后，将纹理特征和V描述子融合为COVID-19严重性估计的评估描述符。与大多数现有方法相比，新描述符包含的信息更多，因此，新方法更适合评估COVID-19肺部感染的严重性。

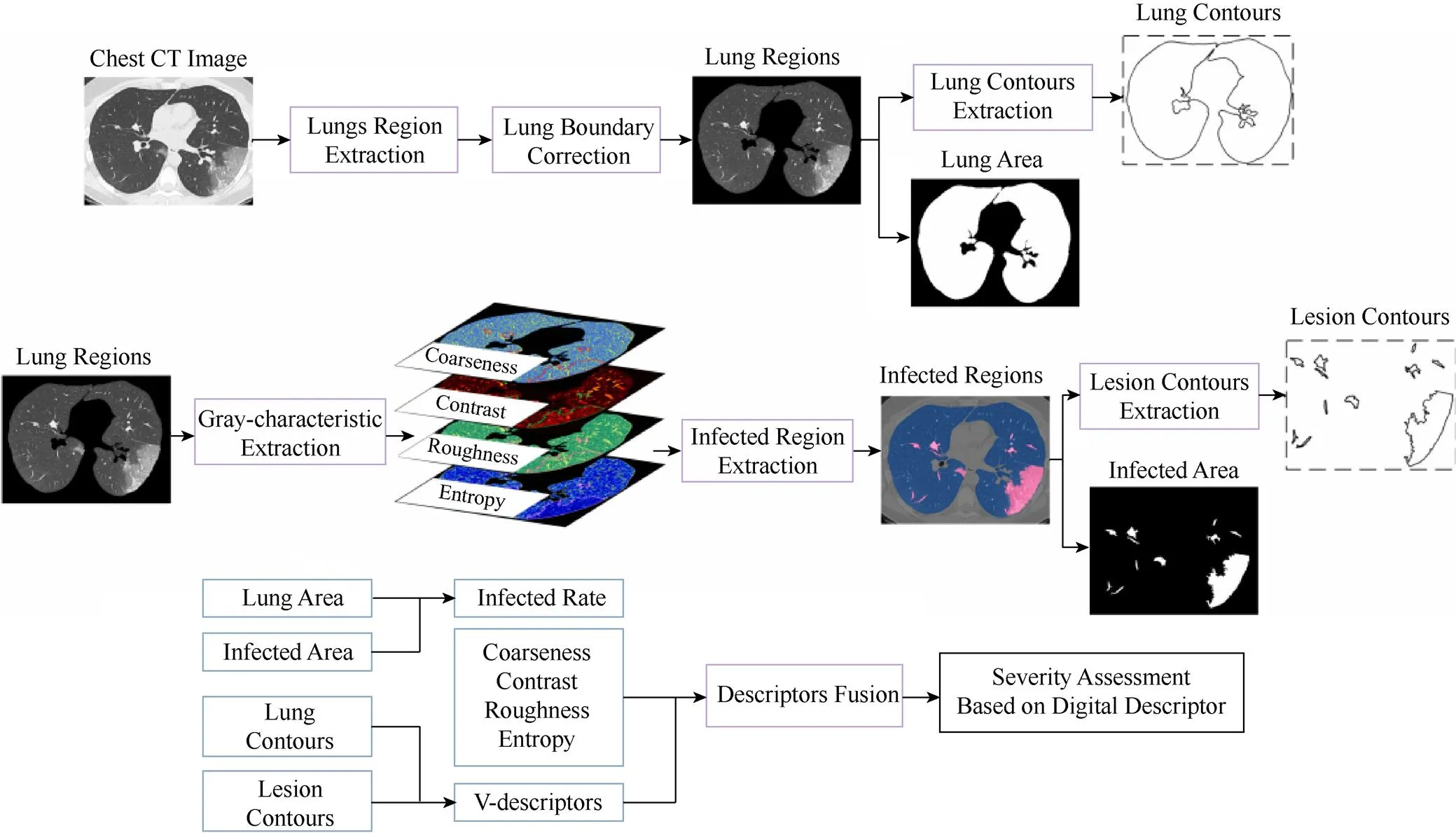
图20 基于V描述子的新冠肺炎评估算法流程图

3 结 论

一百年前，Haar函数与Walsh函数相继面世，且为分段的2值或3值函数。在微积分发展历程中，注重连续函数，对这样的间断对象，其研究成果并不多见。到了上世纪初，人们的关注点大有改变，物理学及工程技术领域的热点话题是间断、跳跃、突变、跨音速、冲击波等。相应地，数学家对非连续函数的研究兴趣出现甚至可以说高涨起来。

Walsh函数和Haar函数都是2[0,1]上的完备正交系，这2类函数的跳跃间断出现在/2处(,为正整数)。其元素的成分，皆为方波或若干个方波的组合，而方波恰是狄拉克函数()经斯切克洛夫平滑算子作用的第一步结果；而引申出的U，V-系统，其结构中的元素均为都是分段多项式，形成了分段多项式族。U，V-系统最突出的特点是函数系中的间断信息，这与物理学及工程技术领域的间断、跳跃、突变等紧密相关，因此均可以用于这些“异类”信号的处理问题。

本文仅对U，V-系统的理论及典型应用进行了阶段性总结，不足与欠妥之处在所难免，希望对本文内容有兴趣的读者提出宝贵意见，我们诚恳欢迎任何批评和建议。

(致谢：齐东旭教授是我国计算几何和计算机图形学学科的主要开创者和引领者之一，U，V-系统是齐东旭教授的重要研究成果之一，他对本文的写作给予热情支持和亲切关怀，在此表示崇高敬意！)

[1] GOTTLIEB D, SHU C W. On the Gibbs phenomenon and its resolution[J]. SIAM Review, 1997, 39(4): 644-668.

[2] JERRI A J. The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations[M]. Boston: Springer US, 1998:1-3.

[3] 齐东旭, 宋瑞霞, 李坚. 非连续正交函数: U-系统、V-系统、多小波及其应用[M]. 北京: 科学出版社, 2011: 1-10, 107-217.

QI D X, SONG R X, LI J. Discontinuous orthogonal functions: u- system, V- system, multiwavelet and their applications[M]. Beijing: Science Press, 2011: 1-10, 107-217 (in Chinese).

[4] WALSH J L. A closed set of normal orthogonal functions[J]. American Journal of Mathematics, 1923, 45(1): 5.

[5] HAAR A. Zur theorie der orthogonalen funktionensysteme[J]. Mathematische Annalen, 1911, 71(1): 38-53.

[6] FENG Y Y, QI D X. A sequence of piecewise orthogonal polynomials[J]. SIAM Journal on Mathematical Analysis, 1984, 15(4): 834-844.

[7] MA H, QI D X, SONG R X, et al. The complete orthogonal V-system and its applications[J]. Communications on Pure & Applied Analysis, 2007, 6(3): 853-871.

[8] GOUPILLAUD P, GROSSMANN A, MORLET J. Cycle-octaveand related transforms in seismic signal analysis[J]. Geoexploration, 1984, 23(1): 85-102.

[9] FENG Y Y, QI D X. A Sequence of piece-wise orthogonal polynomials[R]. MRC Technical Summary Report #2217, Mathematics Research Center, University of Wisconsin- Madison, 1981.

[10] FENG Y Y, QI D X. A Sequence of piece-wise orthogonal polynomials[R]. MRC Technical Summary Report #2229, Mathematics Research Center, University of Wisconsin -Madison, 1981.

[11] 齐东旭, 冯玉瑜. 关于Fourier-U 级数的收敛性[J]. 中国科学技术大学学报(数学专辑), 1983, 13(5): 7-17.

QI D X, FENG Y Y. Convergence of Fourier-U series[J]. Journal of University of Science and Technology, 1983, 13(5): 7-17 (in Chinese).

[12] 齐东旭, 冯玉瑜. 关于一类分段多项式快速变换的注记[J]. 中国科学技术大学学报(增刊), 1983, 13(6): 10-15.

QI D X, FENG Y Y. A note on the fast transform of a class of piecewise polynomials[J]. Journal of University of Science and Technology (suppl), 1983, 13(6): 10-15 (in Chinese).

[13] MICCHELLI C A, XU Y S. Using the matrix refinement equation for the construction of wavelets on invariant sets[J]. Applied and Computational Harmonic Analysis, 1994, 1(4): 391-401.

[14] HUANG C, YANG L H, QI D X. A new class of multi-wavelet bases: V-system[J]. Acta Mathematica Sinica, English Series, 2012, 28(1): 105-120.

[15] 宋瑞霞, 李成华, 王小春, 等. V-系统的小波函数的数学结构[J]. 中国科学: 数学, 2016, 46(6): 867-876.

SONG R X, LI C H, WANG X C, et al. Mathematical structure of wavelet functions of the V-system[J]. Scientia Sinica: Mathematica, 2016, 46(6): 867-876 (in Chinese).

[16] 郭芬红, 熊昌镇. 正交U变换及其快速算法[J]. 中国图象图形学报, 2011, 16(8): 1552-1560.

GUO F H, XIONG C Z. Orthogonal U transform and its fast algorithm[J]. Journal of Image and Graphics, 2011, 16(8): 1552-1560 (in Chinese).

[17] SONG R X, WANG X C, OU M F, et al. The structure of V-system over triangulated domains[M]//Advances in Geometric Modeling and Processing. Berlin: Springer, 2008: 563-569.

[18] 宋瑞霞. 三角域上一类正交函数系的构造[J]. 系统科学与数学, 2008, 28(8): 949-960.

SONG R X. The construction of a new class of orthogonal functions over triangular domain[J]. Journal of Systems Science and Mathematical Sciences, 2008, 28(8): 949-960 (in Chinese).

[19] LIN A J, SHANG P J, MA H. The orthogonal v-system detrended fluctuation analysis[J]. Fluctuation and Noise Letters, 2011, 10(2): 189-206.

[20] 熊刚强, 李子丰, 郭芬红, 等. 一类四进制U-正交函数系[J]. 中国科学: 数学, 2011, 41(2): 145-163.

XIONG G Q, LI Z F, GUO F H, et al. A class of quaternary orthonormal U-system[J]. Scientia Sinica: Mathematica, 2011, 41(2): 145-163 (in Chinese).

[21] 梁延研, 宋瑞霞, 王小春, 等. 完备正交V-系统及其在几何信息重构中的应用[J]. 计算机辅助设计与图形学学报, 2007, 19(7): 871-875, 883.

LIANG Y Y, SONG R X, WANG X C, et al. Complete orthogonal V-system and it's application in geometrical information reconstruction[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(7): 871-875, 883 (in Chinese).

[22] 李坚, 宋瑞霞, 叶梦杰, 等. 基于三角域上V-系统的三维几何模型的正交重构[J]. 计算机学报, 2009, 32(2): 193-202.

LI J, SONG R X, YE M J, et al. Orthogonal reconstruction of 3D model based on V-system over triangular domain[J]. Chinese Journal of Computers, 2009, 32(2): 193-202 (in Chinese).

[23] 宋瑞霞, 陈曦, 孙红磊, 等. 形状群组的分类和检索算法[J]. 计算机辅助设计与图形学学报, 2011, 23(12): 1981-1986.

SONG R X, CHEN X, SUN H L, et al. A novel algorithm of classification and retrieval for shape group[J]. Journal of Computer-Aided Design & Computer Graphics, 2011, 23(12): 1981-1986 (in Chinese).

[24] 张巧霞. 基于三角域上二次V-系统的几何模型的正交重构[D]. 北京: 北方工业大学, 2011.

ZHANG Q X. Reconstructed geometric model by V-system of degree 2 over triangulated domains[D]. Beijing: North China University of Technology, 2011 (in Chinese).

[25] SONG R X, ZHAO Z X, WANG X C. An application of the V-system to the clustering of Chernoff faces[J]. Computers & Graphics, 2010, 34(5): 529-536.

[26] 梁延研, 蔡占川, 李坚, 等. 尺度不变V变换信号消噪[J]. 计算机学报, 2013, 36(9): 1929-1942.

LIANG Y Y, CAI Z C, LI J, et al. Scale-invariant V-transform signal denoising[J]. Chinese Journal of Computers, 2013, 36(9): 1929-1942 (in Chinese).

[27] 王小春, 宋瑞霞, 齐东旭. 三角域上正交W系统的构造与应用[J]. 计算机辅助设计与图形学学报, 2010, 22(9): 1538-1544.

WANG X C, SONG R X, QI D X. The structure of W-system over triangular domains and its application[J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(9): 1538-1544 (in Chinese).

[28] 宋瑞霞, 朱建旺, 王小春. 分形的正交频谱分析[J]. 计算机辅助设计与图形学学报, 2016, 28(3): 488-497.

SONG R X, ZHU J W, WANG X C. Spectrum analysis of fractals based on orthogonal decomposition[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(3): 488-497 (in Chinese).

[29] 陈伟, 乔洁雯, 周晨. 分形曲线生成的频域方法[J]. 中国图象图形学报, 2020, 25(9): 1904-1914.

CHEN W, QIAO J W, ZHOU C. Fractal curve generation method based on the frequency domain[J]. Journal of Image and Graphics, 2020, 25(9): 1904-1914 (in Chinese).

[30] 蔡占川, 孙伟, 齐东旭. 基于正交完备U-系统的图形分类与识别方法[J]. 软件学报(增刊), 2006, 17: 21-27.

CAI Z C, SUN W, QI D X. A Classification and Recognition Method for Planar Figures Based on Complete Orthogonal U-System[J]. Journal of Software (Suppl), 2006, 17: 21-27 (in Chinese).

[31] YE B, CAI Z C, LAN T, et al. A novel shape representation method for complex trademark image[J]. IEEE Access, 2019, 7: 53800-53811.

[32] WANG Z H, LIN H W. 3D shape retrieval based on Laplace operator and joint Bayesian model[J]. Visual Informatics, 2020, 4(3): 69-76.

[33] 陈伟. 二维旋转不变U变换及其应用[J]. 自动化学报, 2016, 42(9): 1380-1388.

CHEN W. 2D rotation-invariant U transform and its application[J]. Acta Automatica Sinica, 2016, 42(9): 1380-1388 (in Chinese).

[34] 陈伟, 张晓婷. 正交旋转不变V矩及其在图像重建中的应用[J]. 自动化学报, 2015, 41(2): 376-385.

CHEN W, ZHANG X T. Orthogonal rotation-invariant V moments and application to image reconstruction[J]. Acta Automatica Sinica, 2015, 41(2): 376-385 (in Chinese).

[35] 宋瑞霞, 孙红磊, 王小春, 等. 边界特征和区域特征相结合的商标检索算法[J], 软件学报, 2012, 23: 85-93.

SONG R X, SUN H L, WANG X C, et al. Trademark retrieval algorithm based on combination of boundary and region features[J]. Journal of Software, 2012, 23: 85-93 (in Chinese).

[36] WANG X C, WANG Y N, SUN H L, et al. Application of a hybrid orthogonal function system on trademark image retrieval[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2014, 8(6): JAMDSM0077.

[37] 宋瑞霞, 王也娜, 李成华, 等. V-系统在形状相似检索中的应用[J]. 计算机辅助设计与图形学学报, 2014, 26(11): 1930-1937.

SONG R X, WANG Y N, LI C H, et al. Application of V-system on shape similarity retrieval[J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(11): 1930-1937 (in Chinese).

[38] 张波, 邹建成, 刘旭丽. 一类新的V描述子在形状识别中的应用[J]. 计算机辅助设计与图形学学报, 2007, 19(7): 920-926.

ZHANG B, ZOU J C, LIU X L. A novel V-system descriptor in shape recognition[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(7): 920-926 (in Chinese).

[39] 刘玉杰, 李宗民, 李华. 三维U系统矩描述子及其快速算法[J]. 计算机工程与应用, 2006, 42(23): 27-30.

LIU Y J, LI Z M, LI H. 3D U system moments descriptor and its fast calculating method[J]. Computer Engineering and Applications, 2006, 42(23): 27-30 (in Chinese).

[40] 刘玉杰, 李宗民, 李华, 等. 三维U系统矩与三维模型检索[J], 计算机辅助设计与图形学学报, 2006, 18(8): 1111-1116.

LIU Y J, LI Z M, LI H, et al. 3D U system moments and 3D model retrieval[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(8): 1111-1116 (in Chinese).

[41] LI Z M, MEN X P, LIU Y J, et al. 3D model retrieval based on V system rotation invariant moments[C]//The 3rd International Conference on Natural Computation. New York: IEEE Press, 2007: 565-569.

[42] LIU Y J, YAO X L, LI Z M, et al. SHREC’08 entry: 3D model retrieval based on the V system invariant moment[C]//2008 IEEE International Conference on Shape Modeling and Applications. New York: IEEE Press, 2008: 249-250.

[43] SONG R X, YAO D X, WANG X C, et al. Retrieval method for 3D object group based on V-system[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2012, 6(3): 340-353.

[44] 丁玮, 闫伟齐, 齐东旭, 基于U系统的数字图象水印技术[J]. 中国图象图形学报: A辑, 2001, 6(6): 552-557.

DING W, YAN W Q, QI D X. Digital image watermarking based on U-system[J]. Journal of Image and Graphics: A, 2001, 6(6): 552-557 (in Chinese).

[45] 王茂森, 邹建成. 基于二次V系统的数字图象水印技术[J]. 北方工业大学学报, 2006, 18(3): 1-5.

WANG M S, ZOU J C. A digital watermarking method based on second degree V system[J]. Journal of North China University of Technology, 2006, 18(3): 1-5 (in Chinese).

[46] 宋瑞霞, 徐燕青, 王小春, 等. V-系统在3D模型数字水印中的应用[J]. 中国图象图形学报, 2015, 20(4): 533-543.

SONG R X, XU Y Q, WANG X C, et al. Application of the V-system to digital watermark of 3D models[J]. Journal of Image and Graphics, 2015, 20(4): 533-543 (in Chinese).

[47] CAO W, CAI Z C, YE B. Measuring multiresolution surface roughness using V-system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1497-1506.

[48] 熊刚强, 齐东旭. 基于U-正交变换的图像编码算法[J]. 中国图象图形学报, 2010, 15(11): 1569-1577.

XIONG G Q, QI D X. Algorithm of image encoding based on U-orthogonal transform[J]. Journal of Image and Graphics, 2010, 15(11): 1569-1577 (in Chinese).

[49] 熊刚强, 齐东旭, 郭芬红. 一种基于全相位双正交三次U变换的JPEG编码的新算法[J]. 自然科学进展, 2009, 19(5): 551-564.

XIONG G Q, QI D X, GUO F H. A new JPEG coding algorithm based on all-phase biorthogonal cubic U transform[J]. Progress in Natural Science, 2009, 19(5): 551-564 (in Chinese).

[50] ZHANG Y M, CAI Z C, XIONG G Q. A new image compression algorithm based on non-uniform partition and U-system[J]. IEEE Transactions on Multimedia, 2021, 23: 1069-1082.

[51] WANG X C, SUN X D, SONG R X. Single image dehazing with V-transform and dark channel prior[J]. Journal of Systems Science and Information, 2020, 8(2): 185-194.

[52] 宋瑞霞, 刚睿鹏, 王小春. 含有大片天空区域图像的去雾算法[J]. 计算机辅助设计与图形学学报, 2019, 31(11): 1946-1954.

SONG R X, GANG R P, WANG X C. Image defogging algorithm for images with large sky region[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(11): 1946-1954 (in Chinese).

[53] 宋瑞霞, 李达, 王小春. 基于HSI色彩空间的低照度图像增强算法[J]. 图学学报, 2017, 38(2): 217-223.

SONG R X, LI D, WANG X C. Low illumination image enhancement algorithm based on HSI color space[J]. Journal of Graphics, 2017, 38(2): 217-223 (in Chinese).

[54] 宋瑞霞, 王孟, 王小春, 等. 基于多层次多方向分解的医学图像融合算法[J]. 计算机工程, 2017, 43(10): 179-185.

SONG R X, WANG M, WANG X C, et al. Medical image fusion algorithm based on multi-layer and multi-direction decomposition[J]. Computer Engineering, 2017, 43(10): 179-185 (in Chinese).

[55] 宋瑞霞, 姚立君, 王小春, 等. 一种基于频域的红外与可见光图像融合新算法[J]. 激光与红外, 2017, 47(9): 1174-1180.

SONG R X, YAO L J, WANG X C, et al. Infrared andvisible images fusion algorithm based on frequency domain[J]. Laser & Infrared, 2017, 47(9): 1174-1180 (in Chinese).

[56] 宋瑞霞, 孙相东, 王小春. 基于HSI颜色空间和暗原色先验的去雾算法[J]. 系统科学与数学, 2017, 37(10): 2111-2120.

SONG R X, SUN X D, WANG X C. Haze removal algorithm based on HSI color space and dark channel prior[J]. Journal of Systems Science and Mathematical Sciences, 2017, 37(10): 2111-2120 (in Chinese).

[57] NAN N, YUE S J, GANG R P, et al. Image super-resolution algorithm based on V-transform combined with neural network[C]//The 5th International Conference on Image and Graphics Processing. New York: ACM Press, 2022: 339-345.

[58] YE B, YUAN X X, CAI Z C, et al. Severity assessment of COVID-19 based on feature extraction and V-descriptors[J]. IEEE Transactions on Industrial Informatics, 2021, 17(11): 7456-7467.

A Survey of theory and applications of U-system and V-system

CHEN Wei1, CAI Zhan-chuan2, LI Jian3, LIANG Yan-yan2, XIONG Gang-qiang4, SONG Rui-xia5

(1. School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi Jiangsu 214122, China; 2. School of Computer Science and Engineering, Macau University of Science and Technology, Macau 999078, China; 3. Faculty of Applied Sciences, Macao Polytechnic University, Macau 999078, China; 4. School of Information Engineering, Guangdong Medical University, Dongguan Guangdong 523808, China; 5. College of Sciences, North China University of Technology, Beijing 100044, China)

The traditional Fourier analysis and continuous wavelet method will produce relatively enormous errors due to the interference of Gibbs phenomenon. To solve this problem, Qi Dongxu proposed the research topic of discontinuous orthogonal function systems, among which U-system and V-system are two typical discontinuous complete orthogonal function systems. In terms of the mathematical theory, U-system and V-system are the results of the extension of the well-known Walsh function and Haar function from piecewise constant to piecewisedegree polynomial, respectively. The most important feature of U-system is that there are both smooth functions and discontinuous functions at various levels in the function system. Therefore, U- and V- systems can process both continuous and discontinuous information, making up for the shortcomings of Fourier analysis and continuous wavelet to a certain extent. This paper reviewed U- and V- systems from two aspects: theory and application. Theoretically, firstly, the construction methods of univariate U-system and V-system were introduced, respectively, then the construction methods of V-system on triangular domain were introduced, and finally the main properties of U- and V-systems were introduced. In terms of application, some representative cases of applications were introduced.

U-system; V-system; orthogonal function; discontinuity; spectral analysis

TP 391

10.11996/JG.j.2095-302X.2022061002

A

2095-302X(2022)06-1002-16

2022-07-31；

：2022-10-19

陈 伟(1986-)，男，副教授，博士。主要研究方向为计算机图形学、信号处理。E-mail：chenwei.must@gmail.com

宋瑞霞(1963-)，女，教授，硕士。主要研究方向为计算机图形学、计算几何。E-mail：songrx@ncut.edu.cn

31 July，2022；

19 October，2022

CHEN Wei (1986-), associate professor, Ph.D. His main research interests cover computer graphics and signal processing. E-mail：chenwei.must@gmail.com

SONG Rui-xia (1963-), professor, master. Her main research interests cover computer graphics and computational geometry. E-mail：songrx@ncut.edu.cn