基于改进人工势场法前车切入场景下的主动避撞路径规划

李胜琴， 孙 鑫

(东北林业大学 交通学院， 黑龙江 哈尔滨 150040)

局部路径规划是主动避撞路径的重要研究内容，对自动驾驶汽车实现避撞起着决定性作用.自动驾驶汽车可利用局部路径规划在存有障碍物的环境中规划出一条从起始位置状态到目标位置状态的避障路径，并满足道路交通的约束条件.

自动驾驶汽车主动避障局部路径规划算法主要有智能规划方法、插值曲线法和人工势场法.人工势场法是由Khatib提出的一种用于机器人运动规划的虚拟力方法[1]，该方法具有计算简单、实时性强、规划路径高效平滑和对检测偏差具有一定的鲁棒性等优点，但存在目标不可达和局部最小值的缺点.因此有部分学者对人工势场法进行了改进.唐志荣等[2]将车辆平面外形简化成长方形，采用椭圆化斥力场边界的概念对传统的人工势场法进行改进，并引入道路边界斥力场模型，但并没有考虑动态情况下的避撞.余政[3]以单向双车道超车行为为研究对象，建立了安全超车约束条件，通过改变斥力势场函数以及建立斥力角旋转对人工势场算法进行改进，但缺少对比，无法体现改进人工势场的优势.翼杰等[4]构建了用于评估道路车辆危险行驶状态的三维虚拟势能场,并确定了各关键参数的计算方法，分析了车辆主动避障过程中的车道保持、换道避障及制动避障等典型驾驶行为,并利用最小势能法获得了各驾驶行为之间的理论判断依据,但该模型只是解决了静态障碍物下的避撞路径规划，未考虑动态场景下的避撞路径规划.

目前对于人工势场的改进有很多，但考虑动态场景的研究相对较少，笔者在考虑汽车行驶安全性和合法性的前提下，提出一种改进人工势场算法，以前车切入的危险场景为研究对象，实现动态避撞路径规划，并通过仿真验证该算法规划避撞路径的有效性.

1 前车切入模型场景描述

1.1 试验场景

前方车辆变道切入本车车道可能会导致两车刮擦、碰撞等交通事故.当目标车遇到前方切入车辆时，一般会采取减速、制动进行避撞，当本车车速过高或切入点距本车过近时，本车无法通过减速、制动进行避撞，可采用转向避撞，为保证转向后可继续按原车速行驶，本车保持原车速进行转向.一般情况下，前车切入场景下的前车车速会比本车车速高，设定本车和前车在城市道路行驶，前车车速不小于本车车速，且换道的第3车道内无行驶车辆及其他障碍物，以该场景为研究内容，对前车切入下的局部避撞路径进行规划，试验场景如图1所示，其中： A为本车，纵向车速vh为40 km·h-1，侧方车辆B从前方切入本车车道，车速vp为60 km·h-1，θ为切入角，是移动障碍车运动方向与本车道车道线的夹角，θ=30°.

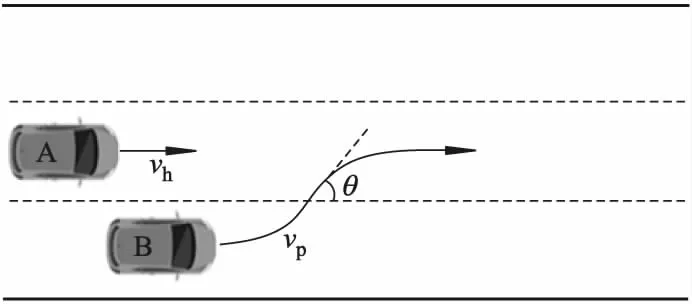
图1 试验场景

1.2 安全距离模型

研究交通场景危险性常使用碰撞时间tc作为评估驾驶安全性的特征值[5]，该指标是综合考量了前后车速间的纵向速度差及纵向相对距离，可在前车切入这一场景对危险等级进行划分.碰撞时间为

(1)

式中:drel为本车与切入车之间的纵向相对距离；vrel为本车与切入车之间的纵向相对速度.

针对驾驶场景的危险性评估，有学者基于3 200余个实际变道场景数据，按照tc值将跟车场景的危险性划分为4种危险级别[6]，如表1所示.

表1 基于tc划分的危险级别

2 改进的人工势场法

2.1 传统人工势场法

传统的人工势场法函数包括引力势场函数和斥力势场函数.传统引力势场的产生是因自动驾驶汽车要到达目标点的需求，自动驾驶汽车与目标点之间的距离是决定引力势场高低的主要原因，通常距离越大，引力势能越大，距离越小，引力势能也随之越小，且距离对引力势能的影响呈指数性变化[7].在二维空间通常将自动驾驶汽车视为一个移动的质点，其起始坐标与目标坐标固定.引力势场函数为

(2)

式中：eatt为引力增益系数；d(q,qg)是矢量，表示汽车的位置q和目标点位置qg之间的欧几里得距离|q-qg|，其矢量方向是从汽车的位置指向目标点位置.

对应的引力为引力场的负梯度，即

Fatt(q)=-∇Uatt(q)=eattd(q,qg).

(3)

传统斥力势场的产生是因自动驾驶汽车朝目标点行驶中遇到障碍物，障碍物可以是运动的动态障碍物，也可以是一直存在或突然出现的静止障碍物.自动驾驶汽车与障碍物之间的距离是决定斥力势场高低的重要原因，距离越大斥力越小，距离越小斥力越大.斥力函数为

(4)

式中：erep的为斥力增益系数；d(q,q0)是矢量，表示汽车的位置q和障碍点位置q0之间的欧几里得距离|q-q0|，其矢量方向是从障碍点的位置指向汽车位置；d0是矢量，为障碍物对自动驾驶汽车产生作用的最大距离.

对应斥力为斥力场的负梯度，即

(5)

自动驾驶汽车由目标点产生的引力势场和由障碍物产生的斥力势场叠加可以得到总的合力势场，自动驾驶汽车受到的合力势场常由一个引力势场和多个障碍物斥力势场叠加而成.当自动驾驶汽车受到来自障碍物的斥力和来自目标点的引力之间存在很大夹角，几乎在同一条直线上时，会出现局部极小值问题.当障碍物和自动驾驶汽车位于目标点的同一侧时，如果受到的斥力和引力大小相等方向相反也会出现局部极小值现象.自动驾驶汽车到达目标点，由目标点产生的引力会降为0，而来自障碍物的斥力不为0，这时自动驾驶汽车已到达目标点，但因斥力势场的作用，并不能停下来，出现目标不可达现象.传统人工势场法因为存在目标不可达和局部极小值的问题，不能保证其规划路径的有效性，需要对传统人工势场法进行改进.

2.2 改进人工势场法

2.2.1改变斥力势场

(6)

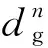
改进后自动驾驶汽车的受力情况如图2所示.

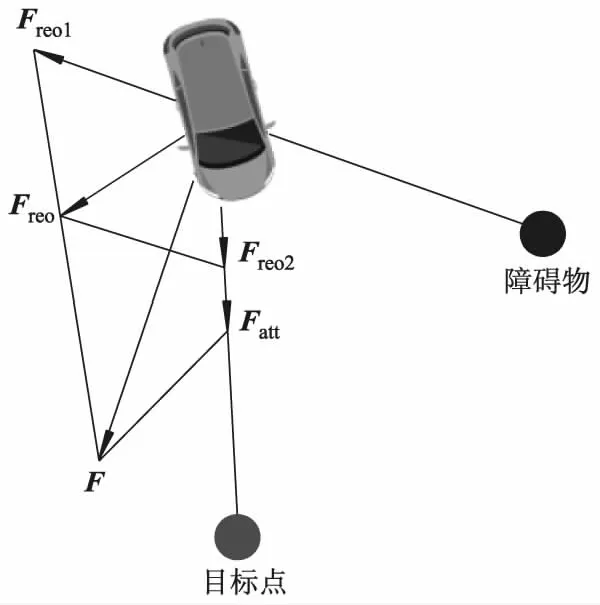
图2 改进后自动驾驶汽车的受力情况

对应改进后的斥力势场函数为

(7)

(8)

式中：Freo1为原斥力，方向从障碍物指向自动驾驶汽车；Freo2为改进后的斥力，方向从自动驾驶汽车指向目标点.

2.2.2增加道路边界势场

自动驾驶汽车在道路上行驶时，不考虑障碍物只考虑道路因素的影响，道路左右边界的危险系数最高，中间位置危险系数最小[9]，根据道路不同位置的危险程度，建立道路边界势场模型，通过建立道路边界斥力势场限制汽车的行驶区域，车道保持的横向移动距离如图3所示.

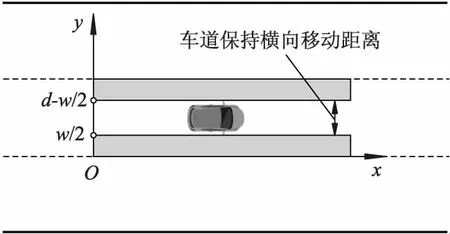
图3 车辆保持的横向移动距离示意图

车速对自动驾驶汽车避撞后的直线行驶也有影响，要考虑车辆速度对斥力场的影响.前车切入下的换道避撞，考虑2个车道的道路边界斥力势场，使自动驾驶汽车换道后依旧可以在道路中间直线行驶，道路边界斥力为

(9)

式中：d为车道宽度；w为汽车宽度；eedge为道路边界斥力的增益系数；v为自动驾驶汽车行驶速度.

4.4.3 气候变暖有助于不耐低温的作物生长，因此要针对引进的优良作物品种进行气候适应性研究，并与本地气候特征进行对比分析，科学合理确定种植制度，做到因地制宜、效益优先。由于气候变暖，使得作物生长季延长，因此，适当调整种植结构，民和县的川水地区可适当扩大冬小麦种植面积。

从式(9)可以看出：道路边界斥力的大小与道路边界斥力增益系数成正比，自动驾驶汽车与道路边界间的距离越小，斥力就越大；自动驾驶汽车与道路边界之间的距离越大，斥力就越小，由此将自动驾驶汽车的行驶区域限制在道路边界内.

2.2.3增加动态斥力势场

传统人工势场法无法对移动障碍物进行势场函数搭建，这是传统人工势场法的一个重大缺陷，针对这一问题对人工势场法进行改进.本研究的场景为前车切入场景，需要考虑切入车的车速以及切入时的角度，因此引入一个动态影响因子ξ.该动态影响因子ξ由纵向影响因子ξx和横向影响因子ξy组成.ξx为移动障碍物在纵向上对本车正常行驶中的影响程度；ξy为切入移动障碍物在横向上对本车正常行驶中的影响程度.计算公式为

(10)

ξy=sinθ，

(11)

ξ=ξxξy，

(12)

式中：vpx为前方切入车的纵向速度；vhx为本车的纵向速度.

一般情况下，动态影响因子ξ越大，该工况就越危险，ξ值越小，危险程度就更低.移动障碍物的动态斥力函数为

(13)

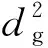
由式(13)可得移动障碍物的动态斥力为

Frep(q)=-∇Urep(q)=

(14)

由式(14)可知，动态影响因子与动态障碍物的斥力大小成正比，自动驾驶汽车距目标点距离与距动态障碍物的实时距离和斥力存在二次指数关系，且动态斥力方向由障碍物指向自动驾驶汽车.

3 试验验证

3.1 增益系数优化

自动驾驶汽车行驶在附着系数较大的路面上，通常要求自动驾驶汽车在转向时的侧向加速度不能超过0.4g，g为重力加速度.通过使用侧向加速度对自动驾驶汽车的转向进行约束，保证自动驾驶汽车在转向时的稳定性、安全性.另外王树凤等[10]研究认为，在紧急工况下，自动驾驶汽车转向时的侧向加速度ay应该被约束在限制值和最大值之间，限制级及最大级分别为

(15)

式中：μ为道路附着系数.

利用MATLAB与Carsim对改进人工势场算法规划避撞路径进行仿真验证.Carsim中的仿真车辆采用c-class、hatchback模型[11].

使用改进的人工势场算法进行路径规划，将本车和切入车看作2个质点，如图4所示.设定自动驾驶汽车行驶的道路宽度为3.750 m，车辆瞬间点位置为(0，1.875)m，障碍物的瞬时点位置为(5.000，0)m.设切入车车速为60 km·h-1，切入角为30°，本车车速为40 km·h-1，经式(1)计算得tc为0.42 s，由表1可知危险等级为4级，濒临碰撞，需要进行避撞路径规划，实现转向避撞.

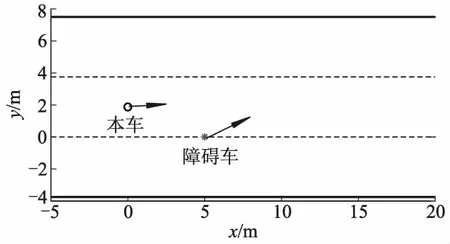
图4 场景示意图

引力增益系数、斥力增益系数和道路边界斥力增益系数对避撞路径均有影响，可以通过正交试验找到确定规划路径最优的增益系数.在切入车速60 km·h-1、本车车速40 km·h-1和前车切入角30°的情况下，对不同增益系数进行组合计算，其影响指标为车辆的侧向加速度.选取的正交表为L9(34),参数设置如表2所示，其中：A、B、C分别代表3种影响因素，A为引力增益系数，B为斥力增益系数，C为道路边界斥力增益系数；3个水平对应因素的不同取值.所设计的正交表如表3所示.

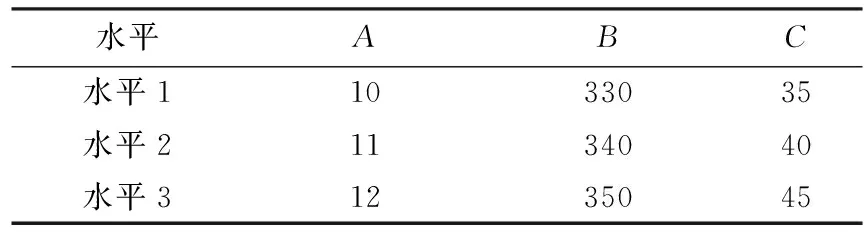
表2 参数设置

表3 正交试验表

表3中试验了9种增益参数搭配方案，利用MATLAB与Carsim的联合仿真，得到侧向加速度，再将侧向加速度填入正交试验表中，计算不同因素下的试验结果平均值，并计算极差，极差反映该因素对试验的影响程度，极差越大，影响程度就越大，通过对每个因素取平均值最小的水平得最优方案.从表3可以看出：引力增益系数对侧向加速度的影响最大，其次是斥力增益系数，再次是道路边界斥力增益系数，引力增益系数对侧向加速度影响最大.根据每个因素的均值可得最优方案为A3B1C2.对应的引力增益系数为12，斥力增益系数为330.道路边界斥力增益系数为40.将改进后规划的路径与未改进路径进行对比，如图5所示.

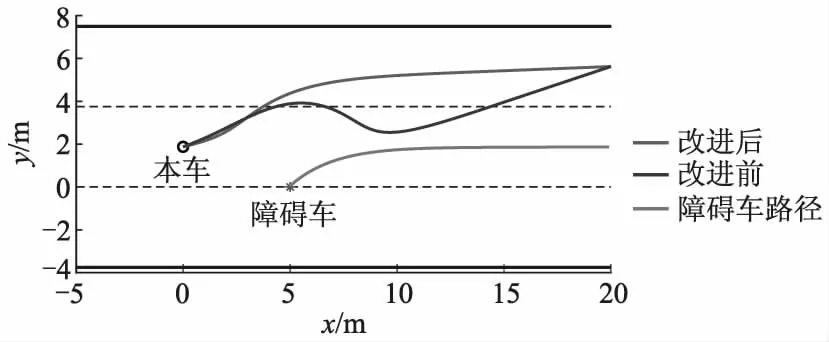
图5 改进前后的规划路径对比

障碍物为切入的汽车，若想实现换道避撞，自动驾驶汽车的侧向位移至少需要1.8 m.从图5可以看出：改进后算法规划出的路径更平滑，自动驾驶汽车沿该路径行驶时侧向移动距离可以更快实现，侧向移动距离更大，避撞时更安全.自动驾驶汽车在未改进算法规划的路径上行驶，因为侧向位移不足，存在碰撞风险，无法实现安全避撞.

3.2 障碍车切入车速不同时的本车运动状态

改变障碍车切入车速分别为40、50、60 km·h-1，切入角度为30°，本车车速为40 km·h-1时进行避撞路径规划，结果如图6所示.仿真试验得到本车侧向加速度、质心侧偏角的变化曲线分别如图7、8所示.

图6 障碍车切入车速不同时的避撞路径

图7 障碍车切入车速不同时本车侧向加速度的变化曲线

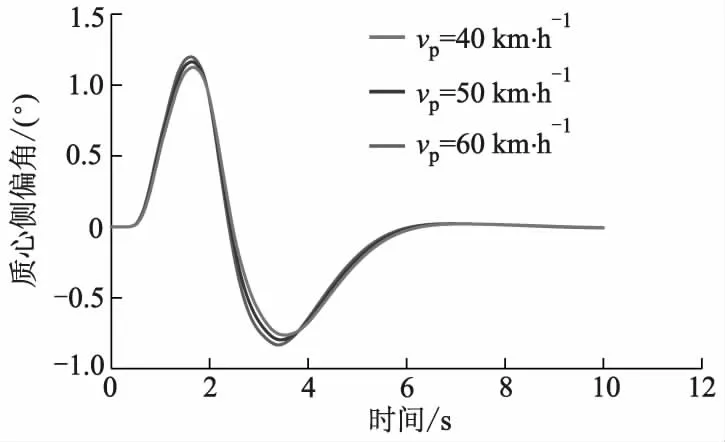
图8 障碍车切入车速不同时本车质心侧偏角的变化曲线

从图6可以看出：障碍车切入车速不同时，算法规划的路径不同，但均平滑且无碰撞风险.从图7可以看出：自动驾驶汽车在不同规划路径行驶时，侧向加速度均小于0.4 m·s-2，沿改进人工势场算法规划的路径行驶时，满足车辆动力学约束条件.刘伟[12]研究表明，普通没有经验的驾驶员通常在自动驾驶汽车质心侧偏角小于2°时可以正常驾驶.从图8可以看出:自动驾驶汽车在不同路径上行驶，其质心侧偏角均在2°以内,满足要求.

3.3 障碍车切入角不同时的本车运动状态

障碍车切入角分别为10°、30°和60°，本车车速为40 km·h-1，切入车速为60 km·h-1，进行避撞路径规划，如图9所示，障碍车切入角不同时改进算法规划出的路径也不同，但规划出的路径均平滑且无碰撞风险.仿真试验得到本车侧向加速度、质心侧偏角的变化曲线分别如图10、11所示，自动驾驶汽车在不同规划路径行驶时侧向加速度均小于0.4 m·s-2，其质心侧偏角均在2°以内，满足正常驾驶条件，沿改进后人工势场算法规划的路径正常行驶，且符合车辆动力学约束条件.

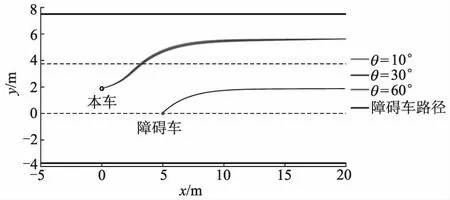
图9 障碍车切入角不同时的避撞路径

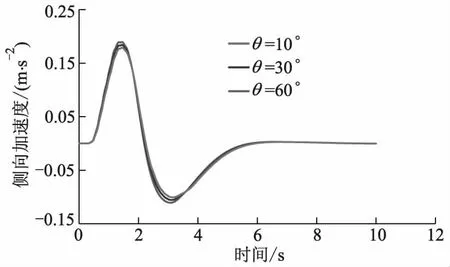
图10 障碍车切入角不同时本车侧向加速度的变化曲线

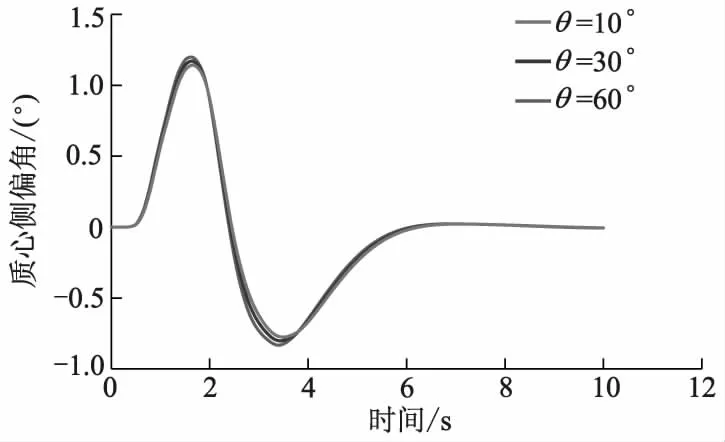
图11 障碍车切入角不同时本车质心侧偏角的变化曲线

3.4 障碍车车速不变本车车速不同时的运动状态

改变本车车速为40、50、60 km·h-1，切入车车速为60 km·h-1，障碍角为30°，进行避撞路径规划，结果如图12所示，仿真试验得到本车侧向加速度、质心侧偏角的变化曲线分别如图13、14所示.

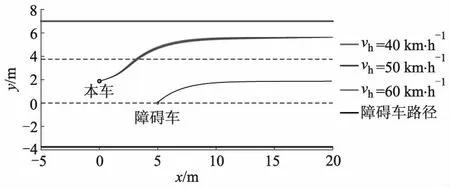
图12 本车车速不同时的避撞路径

图13 本车车速不同时本车侧向加速度的变化曲线

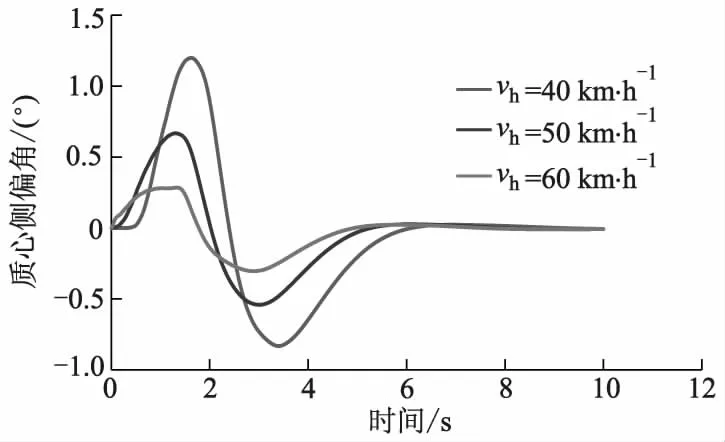
图14 本车车速不同时本车质心侧偏角的变化曲线

从图12可以看出：本车车速不同时算法规划出的路径不同，但规划出的路径均平滑且无碰撞风险.从图13、14可以看出：自动驾驶汽车在不同规划路径下行驶时侧向加速度均小于0.4 m·s-2，说明自动驾驶汽车沿改进人工势场算法规划的路径行驶符合车辆动力学约束条件，其质心侧偏角均在2°以内，也满足正常驾驶条件.

综上所述，自动驾驶汽车躲避前车切入时，使用改进算法可以有效规划避撞路径，且行驶时满足车辆动力学约束，改进后的算法具有可行性.

4 结 论

1) 通过改变斥力势场函数对传统人工势场的斥力场进行改进，增加道路边界斥力势场和引进动态影响因子建立动态障碍物势场，实现前车切入这一动态场景下的避撞路径规划，并对改进前后算法规划的路径进行对比，结果表明改进后算法规划的路径更符合实际要求.

2) 通过正交试验及MATLAB与Carsim的联合仿真得到各个增益系数对自动驾驶汽车侧向加速度的影响程度，确定增益系数搭配的最优方案.对侧向加速度影响程度从大到小的顺序为引力增益系数，斥力增益系数，道路边界斥力增益系数.

3) 分别改变障碍车切入车速、障碍车切入角度和本车车速，对本车路径规划和运动状态进行分析，结果表明：规划的路径平稳无碰撞风险，且自动驾驶汽车沿该路径行驶时满足车辆动力学约束，该算法具有可行性.