基于Optistruct某公交车后围板多目标形貌优化设计

徐明欣，马彩峰，韦淇鹏，陈 剑，苏秀花

（1.柳州五菱汽车工业有限公司，广西 柳州 545007；2.东风柳州汽车有限公司，广西 柳州 545005）

0 引言

在某开发平台上，需要将后对开门更改为公交车封闭行李舱，同时满足降本需求，尽量减少原内板支撑结构，用冲压板材通过合理布置加强筋形式，提高公交车后围板刚度，保证结构频率。

凭借工程师的经验构建多种加强筋方案，然后逐一进行有限元方法验算刚度和模态，得到的只是可行性设计而不是最优设计，这就需要采用先进的优化理念与分析工具寻求最优化的设计。形貌优化是在板金结构中寻找最优加强筋分布的概念设计方法，用来设计薄壁结构的强化压痕，在不增加结构重量的前提下，增加结构的刚度、模态频率等。形貌优化通过定义一个或若干个起筋区域，设定加强筋的最小宽度、起筋角度和高度即可进行计算。同时还可以考虑可加工性，软件提供多种加强筋的布置形式。优化后的加强筋形状可以通过OSSmooth工具直接产生有限元或CAD数据，供设计人员参考[1]。

1 多目标优化函数

通过初步试算，发现公交车钣金后围板在两个位置点刚度较低，优化分析中需要提高两个工况刚度，同时不能降低后围板模态频率，此问题属于多目标优化。在Optistruct中，多目标优化有多种处理方法，比较简单的方法是试算原方案分析结果，将多个优化目标中的一个作为目标函数，其余的目标作为约束响应，比如:柔度不大于原设计的柔度；重量不大于原设计的重量;变形不大于原设计的变形；一阶频率不低于原设计的频率等等。对于某些希望改进的参数，还可以把约束设计更严格，比如重量不大于原来的80%，但这需要经验和反复的尝试[2]。

对于本研究的问题，可以把两个工况刚度综合为一个目标，1阶模态频率作为约束考虑，或者将两个工况刚度和模态频率综合在多目标方程中。前者把两个工况综合为一个目标可以采用线性加权法和最小柔度法来处理。优化是不断尝试的结果，本研究采用3种方法对后围板进行形貌优化分析。

1.1 线性加权和法优化函数

柔度反映的是结构的应变能，是结构刚度的倒数。加权柔度是经典拓扑优化中考虑多工况的一种方法，它是每个独立工况的柔度加权总和，是针对整个结构的全局响应[3]。采用线性加权和法将两个工况刚度转化为单目标问题，同时约束1阶模态频率进行优化求解。

其中，W噪为第K个工况结构柔度加权，一般情况下W噪=1；C噪（ρ）为第K个工况结构柔度，是响应变量；Λ1（ρ）为结构一阶固有频率，是响应变量；CT为常数值。

1.2 最小柔度法优化函数

对于非凸优化问题，线性加权和法不能保证所有工况均得到最优解，现今研究刚度最大问题，可以采用折衷法等效为柔度最小问题来研究。折衷法多目标拓扑优化，即将单独工况载荷集中在一个工况中，用统一工况描述结构综合柔度，同时约束一阶模态频率进行优化求解。

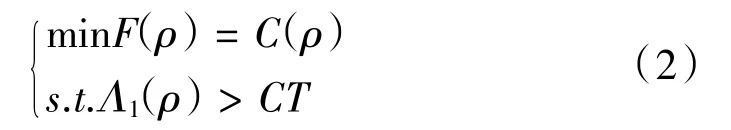
其中，C（ρ）为结构综合柔度，是响应变量；Λ1（ρ）为结构一阶固有频率，是响应变量；CT为常数值。

1.3 多目标方程法优化函数

结构多目标优化同时考虑静态多刚度目标和动态振动频率目标的优化，可以使用多目标优化的综合目标函数[4]。

（3）中，C1（ρ）为噪=1时结构的柔度，是响应变量；为噪=1时原始模型的柔度（原始模型的柔度最大）；为噪=1时单独做柔度优化计算后的柔度（因为经过优化得到最小柔度值）；Λ（ρ）为结构一阶固有频率，是响应变量；Λmax为单独做频率优化计算后的一阶固有频率（经过优化得到最大频率值）；Λmin为原始模型的一阶固有频率（原始模型的频率最小）；w为加权值，设置在0～1之间，一般情况下w=0.5。

2 后围板多目标优化

形貌优化主要用于提高钣金部件的刚度，多数情况下设置的响应类型为节点位移和模态频率值，这两者既可以做约束，也可以做目标函数。在Optistruct软件设置中，要注意加强筋最小宽度推荐值为单元平均尺寸的1.5～2.5倍，起筋角推荐值为60°～75°。形貌优化前，确保设计区域的单元方向一致，勾选缓冲区设置，系统将远离非设计区域放置形状变量，如果不勾选，则筋和非设计空间的边界会产生一个突变。加强筋模式组合中常用的有线性、平面对称等选项。通过上、下边界限制值来边确定起筋方式为凸筋或凹筋，边界忽略表示不保留设计区域内的载荷与约束。

图1为某公交车后围板优化模型，图中浅灰色区域为设计空间。要求加强筋水平放置，且加强筋的最小宽度25 mm、起筋角60°、起筋深度最大15 mm，设置缓冲区，根据优化结果确定凸筋或凹筋，不保留设计区域内的载荷与约束。确定设计变量后，固定约束后围板四周，综合考虑P1点变形、P2点变形和一阶模态频率。

图1 某公交车后围板优化模型

2.1 线性加权和法优化模型

分别在P1、P2两个位置点加载1000 N载荷，并将两种载荷定义在两个工况中。P1、P2点变形通过weighted comp的响应类型，将两个工况线性加权和为一个响应，并设置该响应为最小目标函数，同时约束一阶模态频率大于32 Hz，经过10次迭代计算，得出优化结果。图2是线性加权和优化加强筋分布云图，优化后结构柔度8500 mm/kN，一阶模态频率32.3 Hz。

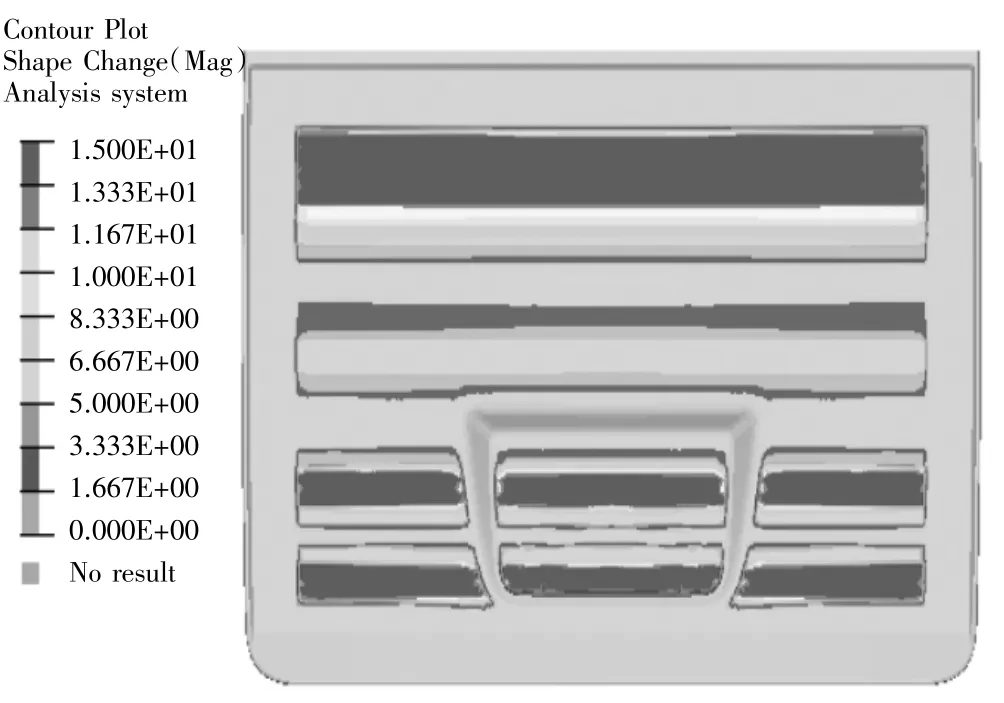
图2 线性加权和优化加强筋分布云图

2.2 最小柔度法优化模型

分别在P1、P2两个位置点加载1000 N载荷，并将两种载荷定义在一个工况中。P1、P2点变形定义为compliance的响应类型，并设置该响应为最小目标函数，同时约束一阶模态频率大于32 Hz，经过11次迭代计算，得出优化结果。图3是最小柔度优化加强筋分布云图，优化后结构柔度8300 mm/kN，一阶模态频率35.0 Hz。

图3 最小柔度优化加强筋分布云图

2.3 多目标方程法优化模型

利用Optistruct中提供的自定义函数考虑结构柔度和模态频率，首先计算出原始模型的柔度为50100 mm/kN、原始模型1阶频率为30.3 Hz、单独最小柔度优化后模型柔度8236 mm/kN、单独最大频率优化后模型1阶频率39.3 Hz。然后按照公式（4）在dequation中编辑软件可识别的自定义函数，接下来定义为function的响应类型，将方程中的变量（柔度和频率）和多目标优化函数关联起来，设置该响应为最小目标函数，经过30次迭代计算，得出优化结果。多目标方程优化加强筋分布云（图4），优化后结构柔度8700 mm/kN，一阶模态频率37.6 Hz。

图4 多目标方程优化加强筋分布云图

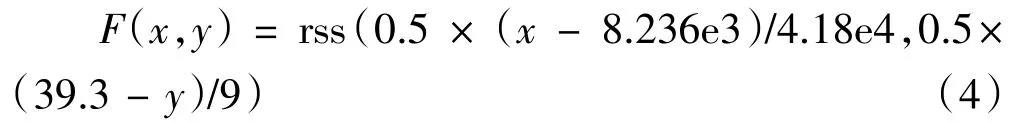
是各种优化方法数据对比见表1。从表中可以看出，最小柔度法优化方法的结构柔度和一阶模态频率均优于线性加权和法优化方案，该方法避免了线性加权和法不保证所有工况均得到最优解的情况，在多目标刚度优化中更具优势。多目标方程优化法可通过加权值来平衡柔度和一阶频率，权重0.5时后围板多目标方程优化方法比最小柔度约束优化方法得出的结构柔度增大5%，一阶频率提高7%。

表1 各种优化方法数据对比

3 后围板优化模型

选用多目标方程优化方法的后围板方案，优化后的加强筋形状通过OSSmooth工具直接产生CAD数据，设计人员在此基础上考虑外观件的美化因素，生成最终数模。是后围板优化模型见图5；原内板支撑结构见图6。原结构重18 kg，优化钣金结构后围板重10 kg，重量降低44%，且原结构存在大量焊接和粘胶工艺，优化结构直接冲压成型即可。

图5 后围板优化模型

图6 原内板支撑结构

在两种方案后围板的相同位置，各选取6个评估点，对不同评估点进行静刚度计算，得出表2各评估点刚度数值，可以看出优化结构较原内板支撑结构刚度分布更均匀，且平均刚度提高22%。

表2 各评估点刚度数值

4 结论

通过三种优化方法的分析结果对比，最小柔度法避免了线性加权和法不保证所有工况均得到最优解的情况，在多目标刚度优化中更具优势。而多目标方程优化法可适用于复杂不同约束的多刚度情况，如车身弯曲工况和扭转工况，同时通过加权值来平衡多个目标响应关系，在多目标优化中应用更广泛。本文优化后设计方案与原方案相比较，柔度下降了83%，一阶固有频率提高了24%，这说明优化在两组变量之间很好地找到了平衡点，较大地提高了部件本身的结构力学和NVH性能。优化后围板结构重量降低44%，评估点平均刚度提高22%，且无焊接和粘胶工艺，较大降低成本，提高结构性能。