面向控制的仿鸽扑翼机纵向动力学建模与分析
2023-01-12彭程孙立国王衍洋谭文倩肖峰
彭程, 孙立国, 王衍洋, 谭文倩, 肖峰
(北京航空航天大学 航空科学与工程学院, 北京 100191)
与一般的固定翼飞机相比,基于扑翼飞行生物仿生学设计的扑翼飞行器具有结构简单、质量轻、飞行机动性和灵活性强及气动效率高等优势,因此,仿生扑翼飞行器的研究已成为世界各国研究的热点[1]。 根据尺寸大小、翅膀扑动的频率及升力产生机理的不同,扑翼飞行器包括仿昆虫型和仿鸟型2 种类型扑翼机。 本文研究的仿鸽扑翼机属于仿鸟型扑翼机[2]。 仿鸟型扑翼飞行器尺寸较大,范围从厘米级到米级不等,其机翼扑动频率不高,小型鸟类一般不超过20 Hz,大型鸟类可能只有1 ~2 Hz,且其机翼相对于整个飞行器的质量占比较大。 仿鸟型扑翼机主要以平飞运动为主,其升力来源于机翼的扑动与空气的相对运动,此外,其机翼扑动在产生升力的同时还为其提供飞行的推动力[3-4]。
扑翼飞行器具有复杂的气动特性[3],想要建立精确的动力学模型非常困难。 面向控制问题建模时虽对精度要求有所降低,但仍具有较高难度,目前仍缺少一个通用模型,在能反映机翼运动产生的惯性力和力矩影响的同时,还能用于控制器设计的验证。 目前,扑翼飞行器的建模主要有2类方法。 一类是较为常用的采用了单刚体假设的牛顿-欧拉法[5-10]。 这种方法将扑翼飞行器视为质量分布均匀的单刚体模型,不考虑机翼扑扭运动产生的惯性力和惯性力矩。 另一类建模方法是将扑翼飞行器视为一个相对运动约束下的多刚体模型[11-13],考虑机翼运动时产生的惯性力和惯性力矩。 Orlowski 和Girard[12]的研究结果显示,当机翼相对于整个飞行器的质量占比达到5. 7%时,扑翼机的单刚体近似模型与非线性多刚体模型的惯性位置、俯仰角和俯仰角速率的仿真结果差别较大,此时多刚体模型更精确。 此外,要建立能用于控制器设计的动力学模型,还需要获取相关的气动系数、气动导数和操纵导数。 Dietl 和Garcia[8]利用Andersen 等[14]使用气动数据计算得到的气动导数和操纵导数,建立了扑翼飞行器面向控制的纵向动力学模型。 Kajak 等[9]利用最小二乘法估计得到了相关的气动系数和操纵导数,建立了无尾扑翼飞行器面向控制的纵向动力学模型。 Jiang 等[10]进一步考虑了尾翼的影响,利用Sun 等[15]给出的气动系数和气动导数及Armanini等[16]给出的操纵导数建立了扑翼飞行器面向控制的纵向动力学模型。 在扑翼飞行器建模的研究中[5-13],Kajak[9]和Jiang[10]等建立的模型属于仿昆虫型扑翼机,Dietl 和Garcia[8]建立的扑翼机尺寸虽然较仿昆虫型扑翼机大,但是其使用气动模型的雷诺数较低,适用于仿昆虫型扑翼机。对于仿鸟型扑翼机,目前还缺少相关的气动导数和操纵导数数据。 因此,在考虑机翼运动惯性力和惯性力矩影响的基础上,如何建立仿鸟型扑翼机面向控制的纵向动力学模型仍然是一个需要解决的问题。
为给仿鸟型扑翼机控制算法的研究提供设计验证平台,仍有待于从自然界鸟类的操纵机理来对仿鸟型扑翼机的动力学模型进行拓展。 结合扑翼飞行生物和微型飞行器的飞行特点,扑翼飞行器往往需要能够改变俯仰力矩的操纵机构来维持或改变俯仰姿态。 例如,李智[6]、Dietl 和Garcia[8]、Jiang 等[10]、年鹏等[17]采用升降舵的偏转角作为输入来改变俯仰力矩,Kajak 等[9]采用压力中心的水平位置来改变俯仰力矩。 此外,扑翼飞行器还需要以机翼的扑动速度作为输入来改变飞行时的推力,其中机翼在一个扑动周期内的平均扑动速度可以通过控制机翼的扑动角振幅[6,8]、扑动角位移[17]、扑动频率[6,9,18]等来改变。 然而,自然界中的鸟类在飞行中除了通过偏转尾翼来维持纵向姿态平衡及改变翅膀的扑动振幅或频率来改变飞行推力外,还会扭转翅膀来配合翅膀的扑动,以调节翅膀产生的升力方向。 但是,目前针对包含机翼扭转角振幅的面向控制的三输入仿鸟型扑翼飞行器纵向动力学模型仍有待于研究。
综上所述,为给仿鸟型扑翼机控制律设计提供通用验证平台,本文建立了三输入定扑动周期的仿鸽扑翼机线性时变周期系统模型,并进行了动稳定性分析和开闭环时域仿真分析等多角度的验证。 首先,考虑机翼运动产生的惯性力和惯性力矩的影响,利用Kane 方程建立了仿鸽扑翼机的多刚体非线性模型;其次,选择升降舵偏转角、机翼扑动角振幅和机翼扭转角振幅作为控制输入,结合已有气动数据及计算模型[19-22]工程估算了扑翼机的气动导数系数和操纵导数系数,建立了面向控制的仿鸽扑翼机纵向多余度线性时变周期系统模型;然后,基于Floquet 理论对该线性时变周期系统模型进行了动稳定性分析;最后,在设计基础控制器和控制分配方法的前提下,进行了开环和闭环仿真分析验证,阐释了模型的可信性及机翼扭转角振幅的引入对飞行操控能力的改善效果。
1 仿鸽扑翼机线性时变周期系统模型的建立
1.1 仿鸽扑翼机的多刚体模型
仿鸽扑翼机模型包含机身、一对对称的机翼和尾翼。 机翼通过铰链与机身相连接,绕xb轴上下扑动,同时绕机翼中心线扭转运动,扑动角为φ,扭转角为η,如图1 所示。

图1 仿鸽扑翼机概念示意图Fig.1 Diagram of a pigeon-like flapping-wing aircraft
仿鸽扑翼机稳定飞行时,机翼的扑动和扭转运动是周期性的,为了方便表示机翼的运动规律,参照Dietl 和Garcia[7]的方法将机翼扑动和扭转分别简化为频率为f1和f2的正弦运动:

式中:A为机翼扑动角振幅;R为机翼扭转角振幅;t为时间;φ1和φ2分别为扑动和扭转的相位角。
由于自然界中鸽子身体、翅膀的形状极不规则且在飞行中不断变化,要获取其精确的外形几何数据非常困难,为了方便分析,参照Orlowski 和Girard[12]的简化方法,考虑机翼扑动产生的附加惯性力和惯性力矩的影响,将扑翼机简化为图2所示的多刚体模型。 机身简化为一个质量均匀的圆柱体,长度为l,半径为r;左右机翼的形状简化为矩形,机翼展长为l1,单机翼质心到机身尾翼组合体质心距离为l2,单机翼弦长为l3;尾翼简化为矩形薄板,单个尾翼长、宽分别为l4、l5,左右两边尾翼作为仿鸽扑翼机的升降舵,由联动机构连接,同时偏转相同角度;机身尾翼组合体、左侧机翼、右侧机翼的质量分别为m1、m2、m3,其中m2=m3,机翼质心位于机翼几何中心,机身质心到机翼前缘的距离为xg,全机总质量为m,其中m1、m2和m3前“*”表示重心位置。 需要说明的是,由于在较低的飞行速度下鸟类飞行的升力和推动力主要由翅膀扑动产生,为了方便分析,主要考虑仿鸽扑翼机机翼扑动产生的气动力而忽略机身的气动力,因此,由机身形状的不同而产生的对全机气动力的影响可以忽略。
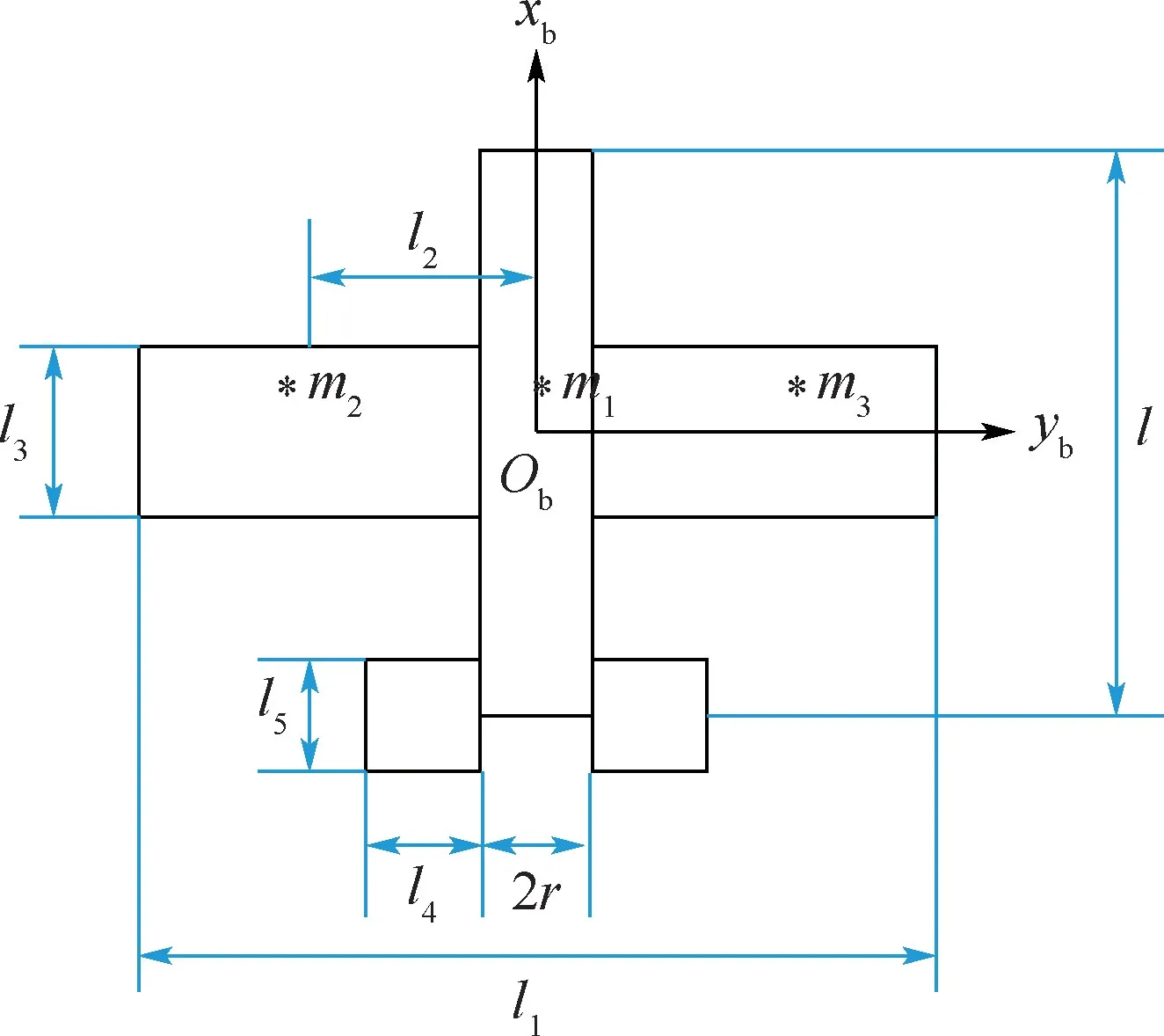
图2 仿鸽扑翼机简化模型Fig.2 Simplified model of pigeon-like flapping-wing aircraft
由于采用Kane 方程可以避免方程中出现对静矩的求导项,容易将动力学方程化为标准形式,便于编程计算[23],采用Kane 方程建立如式(3)所示的仿鸽扑翼机纵向多刚体动力学模型:
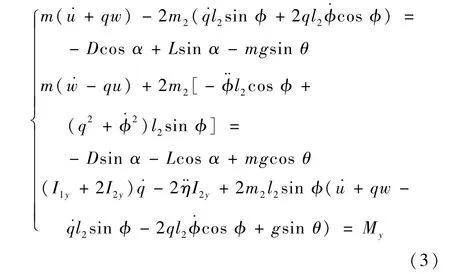
式中:u、w分别为扑翼机相对于地面参考系的速度在机体轴xb、zb方向的分量;q为扑翼机相对于地面参考系的俯仰角速度在机体轴上的分量,˙q、¨q分别为导数和二阶导数;θ为扑翼机相对于地面坐标系的俯仰角;α为扑翼机飞行迎角;L、D、My分别为扑翼机所受的升力、阻力、俯仰力矩,其与扑翼机飞行速度V、雷诺数、扑翼机飞行迎角α及机翼扑动时的平均迎角αw有关;I1y为机身在yb轴上的惯性矩,I2y为机翼在yb轴上的惯性矩。
该扑翼机模型的几何参数和机翼运动参数如表1 所示。

表1 仿鸽扑翼机几何参数Table 1 Geometry parameters of pigeon-like flapping-wings aircraft
当扑 翼 固 定 时,φ=η===== 0,式(3)为传统的固定翼飞机的纵向动力学方程,与其相比较,式(3)中包含和的项为机翼扑动引起的惯性力或力矩,包含¨η的项为机翼扭转引起的惯性力矩,多出来的其他项为机身运动引起的机翼产生的惯性力或力矩。
1.2 仿鸽扑翼机操纵机制
为阐明仿鸽扑翼机的操纵机制及设计依据,一方面,选取常规的升降舵偏转角作为操纵输入;另一方面,为了方便工程实践和系统建模分析,在定周期条件下选取机翼扑动角振幅和扭转角振幅作为操纵输入。 其中,升降舵偏转的变化可以通过伺服舵机电压的变化来工程实现;定周期下的机翼扑动角和扭转角振幅的实时变化可以通过无刷电动机、伺服舵机和无级调幅扑翼驱动机构[24]来工程实现。
本节以机翼扑动角为例,阐释仿真中定周期、变振幅的机翼扑动角在各离散采样时刻的实时变化情况。 在各个离散的采样时刻,机翼扑动角的变化如下:
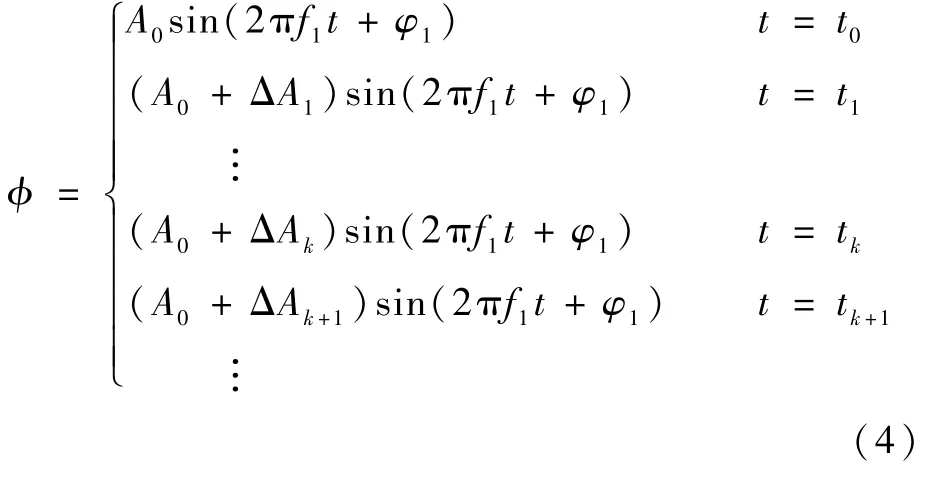
即在t=tk时刻,机翼扑动角位于振幅为(A0+ΔAk)的正弦轨迹线上。 以扑动频率10 Hz,扑动基准角振幅A0,仿真步长0.005 s,初始相位φ1=0 为例,机翼扑动角在一个周期为20 个离散采样点的变化曲线如图3 所示。
图3 中,机翼扑动角在一个周期T内的各采样时刻点的值如下:

图3 分时段变振幅扑动序列示意图Fig.3 Diagram of flapping sequence of time-varying amplitude
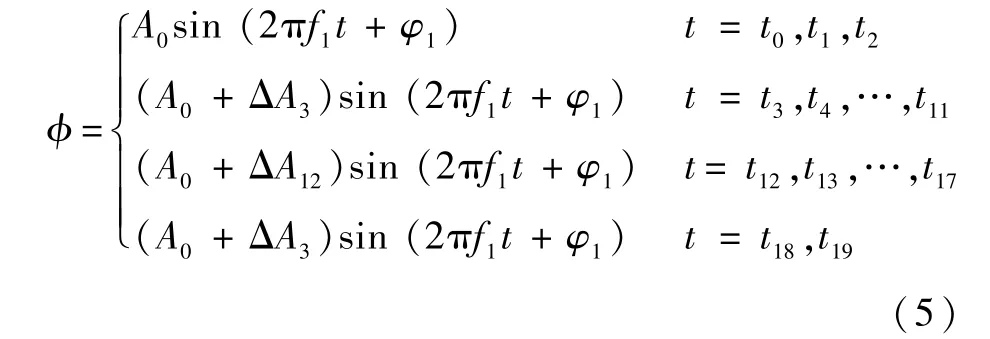
1.3 面向控制的线性时变周期系统模型的建立
为了方便后续线性时变周期系统的分析及控制系统的设计,本文对扑翼机非线性运动方程(3)解耦并进行小扰动线性化。 选择仿鸽扑翼机升降舵的偏转角变化量Δδe、机翼扑动角振幅相对于基准值的变化量ΔA及机翼扭转角振幅相对于基准值的变化量ΔR来作为被控对象的控制输入,即控制输入为v= [ΔδeΔAΔR]T;扑翼机纵向状态量相对于配平值的偏差为x=[uwqθ]T;选定速度为10 m/s、高度为20 m表示基准飞行状态,在基准飞行状态下的配平值如表2所示。

表2 配平值Table 2 Trimming values
最终得到扑翼机的线性状态方程:

式中:
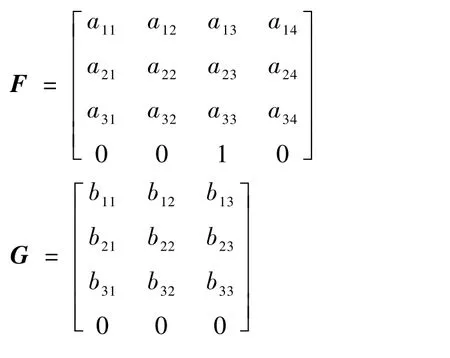
F中各元素由气动系数和气动导数构成,在气动系数方面F中各元素与升力系数CL、阻力系数CD和俯仰力矩系数Cm有关,在气动导数方面,a11、a21、a31与升力、阻力、俯仰力矩对速度u的导数Lu、Du、Mu有关,a12、a22、a32与升力、阻力、俯仰力矩对速度w的导数Lw、Dw、Mw有关,a13、a23、a33与升力、阻力、俯仰力矩对角速度q的导数Lq、Dq、Mq有关。G中各元素由操纵导数构成,其中b11、b21、b31与升力、阻力、俯仰力矩对升降舵偏转角δe的导数Lδe、Dδe、Mδe有关,b12、b22、b32与升力、阻力、俯仰力矩对机翼扑动角振幅A的导数LA、DA、MA有关,b13、b23、b33与升力、阻力、俯仰力矩对机翼扭转角振幅R的导数LR、DR、MR有关。F和G中各元素的具体表达式可以通过小扰动线性化推导得到。 为获取F和G随机翼运动的周期变化情况,本节将对仿鸽扑翼机的气动系数、气动导数系数及操纵导数系数进行计算。
1.3.1 总气动系数计算
特定扑翼翼型下的CL、CD、Cm大小与雷诺数Re、扑翼机飞行迎角α、机翼扑动时的平均迎角αw有关,而αw又与α、A、f1、R、f2、机翼尺寸大小及扑动扭转相位有关。 因此,CL、CD、Cm的大小由Re、α、A、R、f1、f2、t及机翼尺寸大小等元素共同确定。 由于仿鸽扑翼机的尺寸大小、飞行速度、Re与DOVE 扑翼机[25]基本相似,采用与DOVE 扑翼机相同的NACA4408 扑翼翼型,并结合其在Re为70 000 时CL、CD、Cm随迎角的变换规律[20]和夏风[19]给出的计算模型,计算得到各个采样时刻机翼运动产生的CL、CD、Cm大小。 在表2 中选定的基准飞行状态及表3 设定的基准机翼运动参数下,即Re、α、f1、f2均已设为定值,此时可以获得在不同的A和R下,扑翼机的CL、CD、Cm在扑动周期内的变化,其变化情况如图4 和图5 所示。
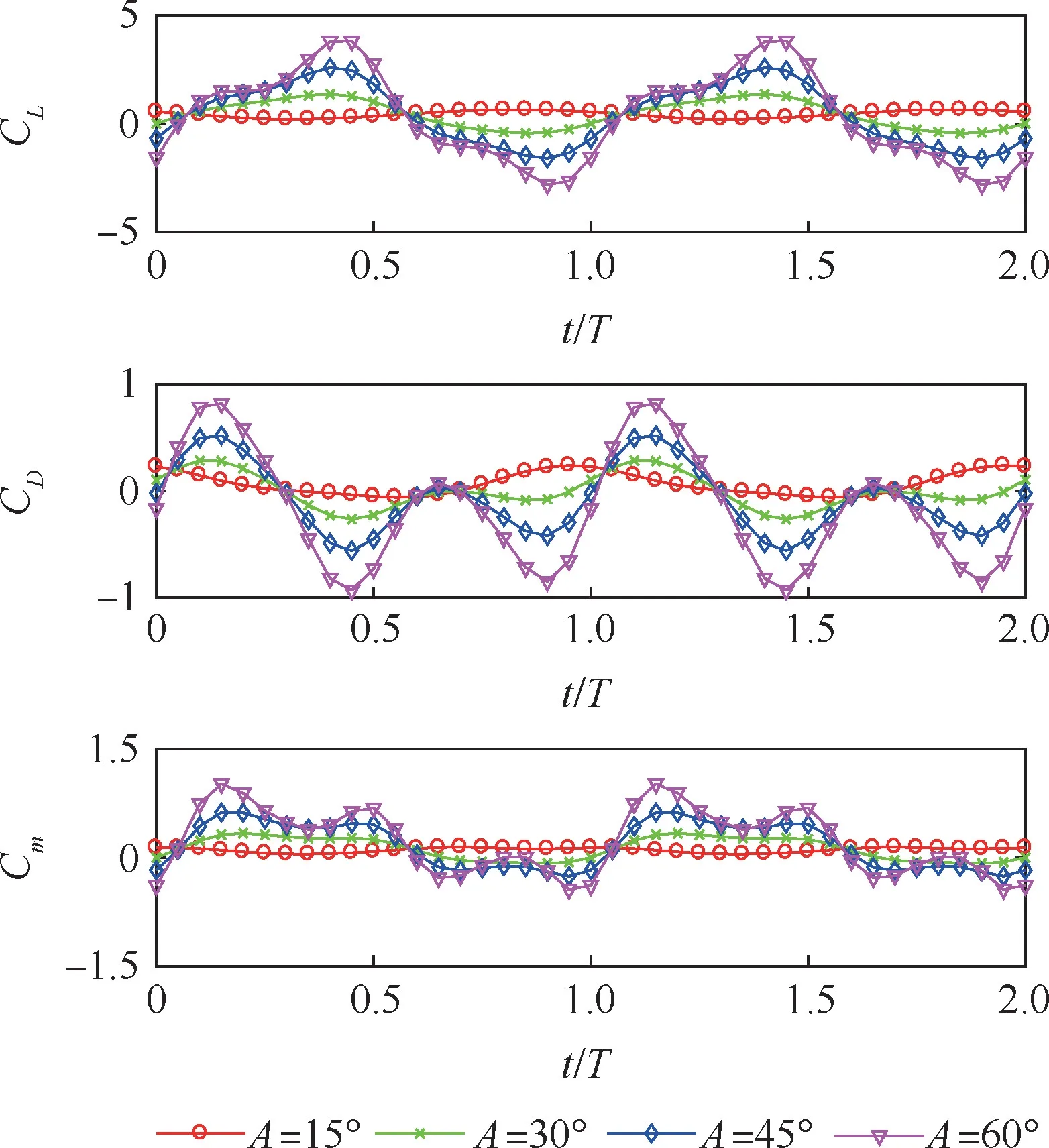
图4 不同机翼扑动角振幅下气动系数的变化Fig.4 Variation of aerodynamic coefficients with different amplitudes of flapping-wing angle
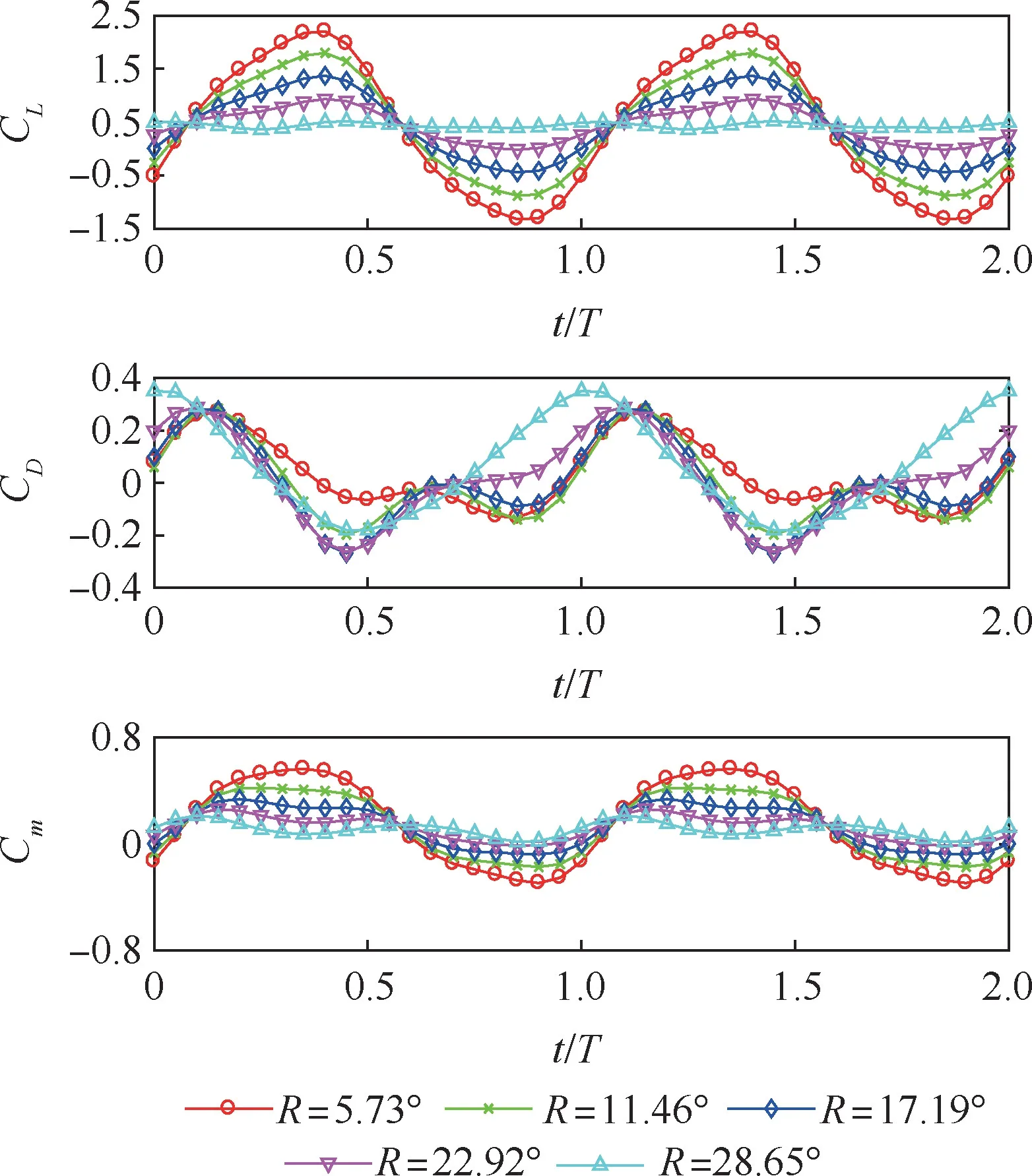
图5 不同机翼扭转角振幅下气动系数的变化Fig.5 Variation of aerodynamic coefficients with different amplitudes of wing torsional angle
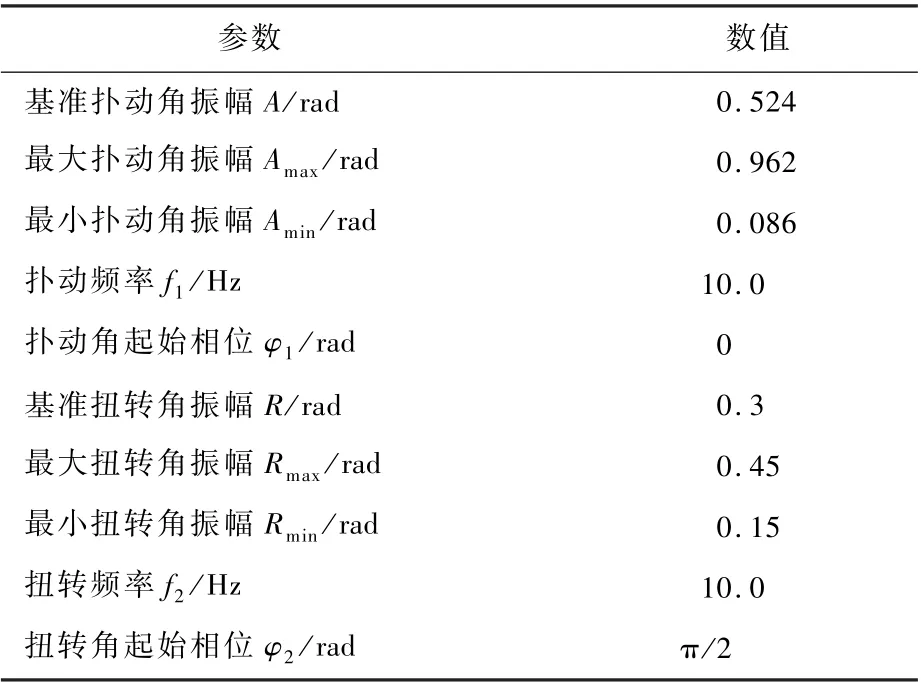
表3 机翼运动参数Table 3 Motion parameters of wings
由图4 可以看出随着A的增大,扑翼机的CL、CD、Cm的振幅增大,CD的平均值减小,即推力的平均值增大,这与自然界中鸟类的飞行特点相符合。 此外,在A=15°时CL、CD、Cm变化较为平缓,且CL的变化趋势与其他3 个不同角振幅下的变化趋势相反,这是因为角振幅过小时机翼的扑动速度减慢,此时机翼的迎角主要受到扭转的影响。 另外如图5 所示,当R增大时,CL的振幅减小,Cm的振幅也减小。 因此,可以期望通过调节R来减缓扑翼机飞行中由于CL和Cm的变化引起的θ的振荡和最大的法向过载。 此外,R不能无限增大。 当R过大时,会造成机翼扑动时迎角方向反向,从而造成升力反向,使飞行不稳定。 由图5可以看出R=28.65°时CL已经开始出现反向,因此A=30.03°时,R不宜超过28.65°。 图4和图5 中T为周期,1T=0.1 s。
1.3.2 气动导数系数和操纵导数系数估算
由于仿鸽扑翼机的平尾布局和作用与常规布局飞机类似,可以采用常规布局飞机的飞行动力学[21]对其进行估算。 其中,平尾尾容比Aht、平尾力臂lht及平尾升力线斜率CLα,t等参数将直接影响气动导数系数和操纵导数系数的大小,因此,选取合适的Aht、lht/¯c(¯c为平均气动弦长)及CLα,t至关重要。
本文中的仿鸽扑翼机取Aht= 0. 37,lht/¯c=1.67,对比表4 的扑翼机平尾容量系数典型值可以知道其Aht和lht/¯c的大小均在合理范围内。 平尾翼型参考熊超[22]使用的尾翼翼型,其CLα,t=2.92,效率系数ηe=0.85。 基于Aht和lht/¯c的数值大小及平尾的翼型和形状,可以估算得到仿鸽扑翼机的气动导数系数和升降舵的操纵导数系数。 此外,分别由图4 和图5 中的曲线插值可以得到A和R的操纵导数系数。 本节给出了气动导数系数和操纵导数系数的估算方法及重要参数的选取依据,进而可以得到气动导数系数和操纵导数系数的具体数值。
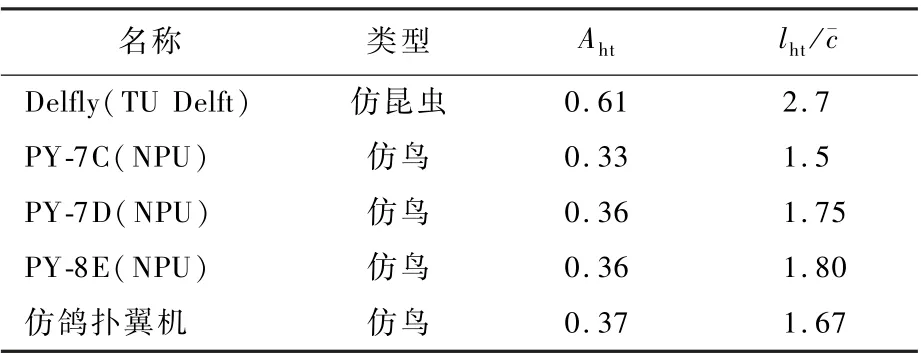
表4 扑翼机尾容量系数典型值[22]Table 4 Typical values of tail capacity coefficient of flapping-wing aircraft[22]
至此,获得了仿鸽扑翼机线性模型中所需的气动系数、气动导数系数及操纵导数系数,构建了一个完整的面向控制的线性时变周期系统模型。
1.3.3 状态矩阵特征值分析
在如式(6)所示的仿鸽扑翼机线性时变周期系统中,状态矩阵F的特征值变化及短周期阻尼比和自振频率变化情况如图6 所示,其中,T为周期,1T=0.1 s。

图6 F 的特征值变化Fig.6 Eigenvalues of F
可以看到,机翼的周期性扑动使得线性时变周期系统F中的模态极点周期性变化。 其中,2 个离虚轴较远的短周期模态极点的周期性变化表明系统短周期的阻尼比和自振频率周期性变化,短周期平均阻尼比为0.399 9,短周期平均自振频率为10.371 2 rad/s。 虽然短周期模态周期性变化,但其是稳定的,这是合理地选择平尾尾容比和平尾力臂等参数的结果。 此外还可以看到,2 个离虚轴较近的特征值在复平面的左右两边来回运动,这意味着该系统存在静不稳定的模态。因此,扑翼机是否周期稳定并不能由F直接确定,必须通过Floquet 动稳定性分析确定。
1.4 控制输入各通道操纵效率分析
本节在基准飞行状态下,以估算得到的操纵导数系数为原始数据,用G中各元素的表达式,计算得到仿鸽扑翼机的各输入通道的操纵效能,并对其进行分析,以明确各输入的操纵作用,从而为控制器的设计提供依据。
在2 个扑动周期内,扑翼机升降舵偏转的操纵效能、机翼扑动角振幅的操纵效能及机翼扭转角振幅的操纵效能如图7 所示,其中T为周期,1T=0.1 s。
如图7 所示,升降舵的偏转主要使q的平均值发生变化,从而改变扑翼机的俯仰姿态和平衡扑翼机的俯仰力矩。
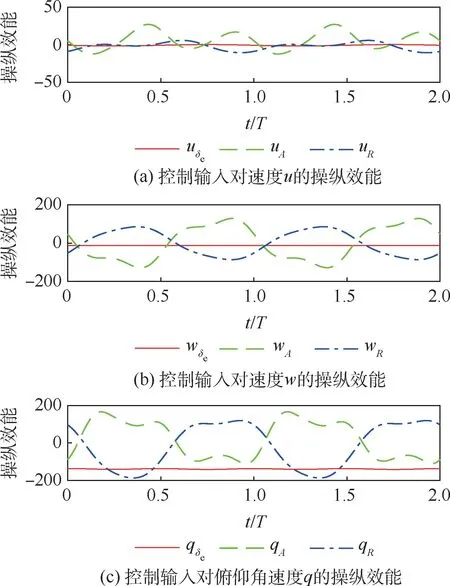
图7 控制输入的操纵效能Fig.7 Control efficiency of inputs
此外,uA、wA及qA随机翼的周期扑动而周期变化且其振幅都特别大,这是因为扑翼机的升力和推力主要是由机翼的扑动产生,而扑翼的升力和推力中心线不是一直通过扑翼机重心,而是随着机翼的扑动不断地变化。 在一个周期内,uA、wA和qA的平均值分别为5. 066 6 m/(s·rad)、0.676 7 m/(s·rad)和19.752 4 s-1。 可以看到,A增大可以使u增大,这与增大A来增大扑翼机推力的操纵机制相符合。 另外,由于qA的平均值较大且振幅较大,A的改变必将引起q的改变。因此,对扑翼机纵向俯仰姿态的控制需要升降舵和机翼扑动角振幅共同配合来完成。
由图7 可知,R增大对u、w和q的平均值影响很小,且对q的平均值影响可以通过升降舵来调节。 另外,在一个扑动周期内,wR的振动方向与wA相反,qR的振动方向与qA相反,uR的最大值相对于uA较小。 因此,在增大A的同时调节R的大小可以减缓扑翼机飞行时q和θ的振动及法向过载nz的振动。
2 基于Floquet 理论的线性时变周期系统的动稳定性分析
考虑到Floquet 理论具有较高的准确性[26],本节采用该理论对机翼质量占比为6.67% 的仿鸽扑翼机线性时变周期系统进行动稳定性分析。
当存在小扰动量时,线性时变周期系统的微分方程为

式中:F(t)∈Rn×n且F(t+T) =F(t),x(t)∈Rn×1。式(7)的基解矩阵为非奇异矩阵ψ(t)∈Rn×n。
存在非奇异常值矩阵C∈Rn×n满足:

矩阵C的特征值ρ1,ρ2,…,ρn即为式(7)的特征乘子。 根据Floquet 理论,可以获得以下关系:

式中:k∈N。 此时扰动状态量xj随时间的变化与矩阵C的特征值大小有关。 当矩阵C所有的特征值都在单位圆内时,扰动量将随时间的增加而逐渐消失,系统稳定;否则系统不稳定。
在基准飞行状态下,C的特征值为

矩阵C特征值模的最大值大于1,在单位圆外,系统动不稳定。
3 仿真分析
3.1 开环仿真结果
在基准飞行状态下,给升降舵一个脉冲信号,仿鸽扑翼机的开环响应如图8 所示。
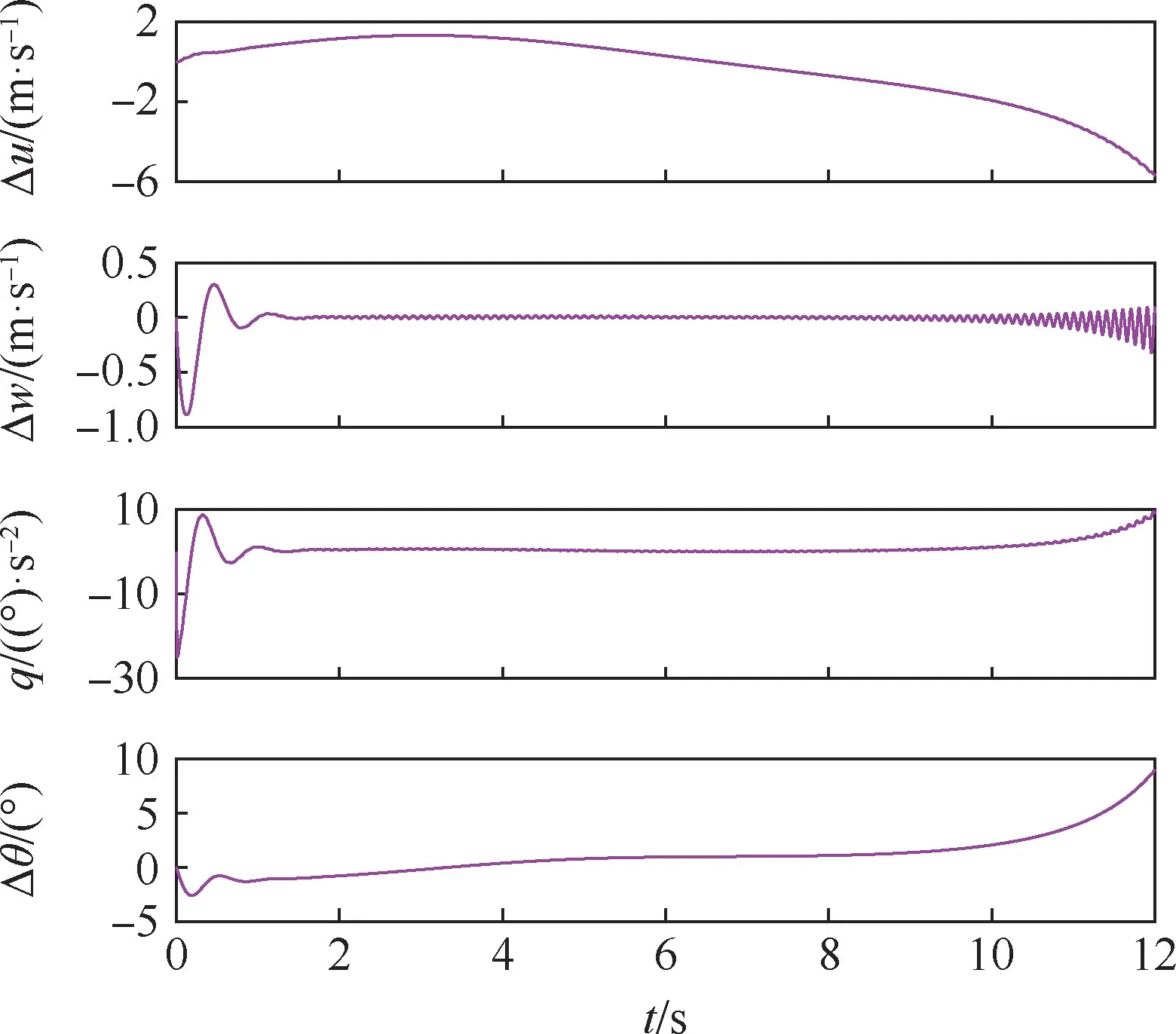
图8 升降舵脉冲信号下的开环仿真响应Fig.8 Open-loop simulation response under elevator pulse signal
如图8 所示,在给升降舵一个脉冲激励信号后,在短时间范围内,w和q较快地稳定下来,仿鸽扑翼机具有稳定的短周期模态,与1.3.3节分析结果一致。 在长时间范围内,u发散,而其他3 个状态量先是稳定在一个值上,最终随着u的发散而发散,这与第2 节的分析结果一致。
3.2 经典控制器设计
利用串级PID 经典控制算法设计了图9 所示的纵向轨迹跟踪控制器,以Δδe、ΔA和ΔR作为控制输入,高度h和u作为输出。 此外,针对操纵输入的冗余问题,考虑到有效集方法具有计算方便、步骤简单、实时性好等优点,采用有效集方法[27],进行控制分配器的设计,实现了升降舵和机翼扭转角振幅对俯仰姿态角回路的联合控制,其中ucmd为需要跟踪的u的指令信号,hcmd为需要跟踪的h指令信号,符号上方“ -”表示负反馈。
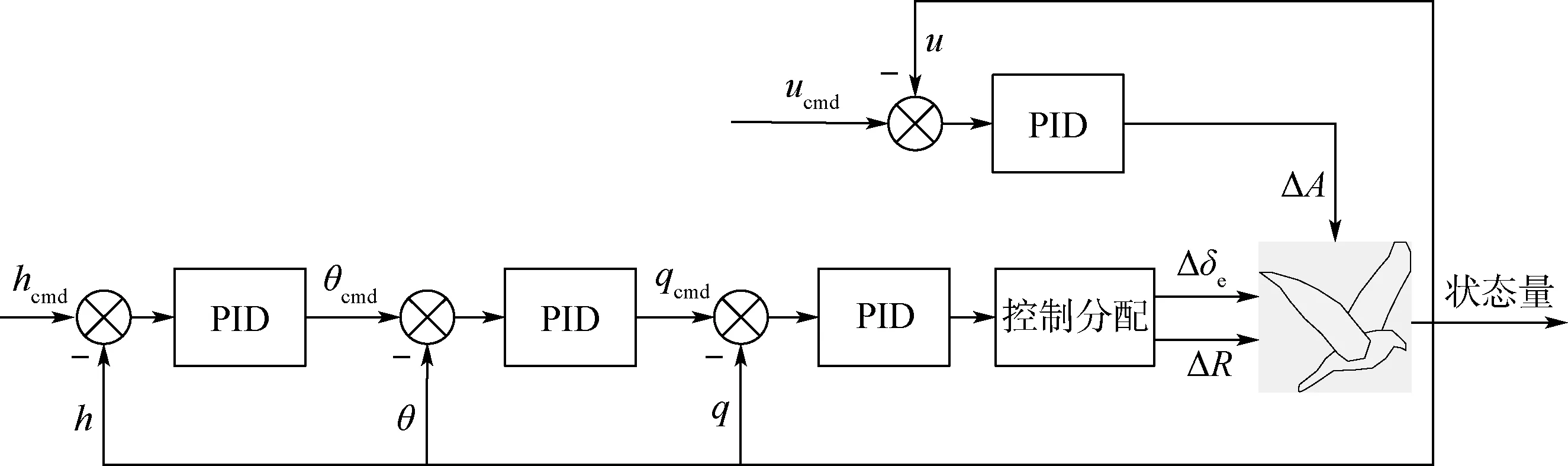
图9 纵向双通道闭环控制器结构Fig.9 Structure of longitudinal dual channel closed-loop controller
3.3 闭环仿真分析
在基准飞行状态下,给定一组周期为40 s、振幅为5 m 的正弦高度指令信号,对闭环系统进行仿真。 为了验证将ΔR作为控制输入的效果,将采用带控制分配的Δδe、ΔA和ΔR的三输入闭环仿真结果与只采用Δδe和ΔA二输入的闭环仿真结果进行对比。 最终的状态量响应和操纵响应分别如图10 和图11 所示。
由图11(a)可以看出,扑翼机要跟踪h指令时,首先要偏转Δδe来改变q,从而改变θ来实现h的变化,同时,由图11(b)可以看出,为了避免h变化引发的u变化,要改变ΔA来改变机翼扑动的速度。 此外,由图10(a)、图11(a) 和图11(b)可以看到,扑翼机并不是完全依靠Δδe来改变俯仰姿态,如在30 ~40 s 扑翼机上升时,Δδe处于上偏状态,这是因为此时A增大,其在产生推力的同时也会产生俯仰力矩从而对q产生影响,这一点也与图7 中qA的平均值19.752 4 s-1相符合。因此,对扑翼机俯仰姿态的操控是通过Δδe和ΔA的变化共同来完成。
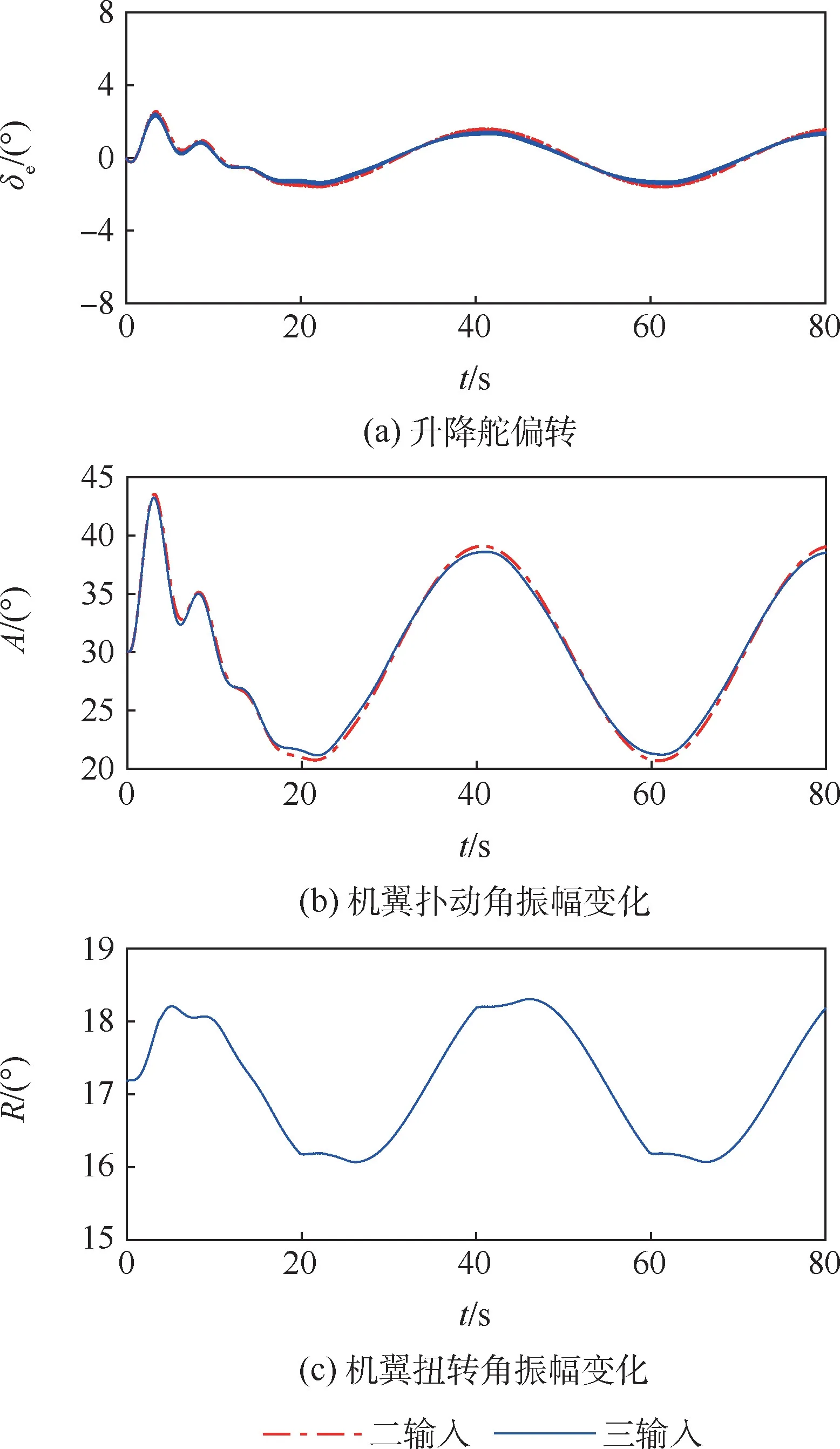
图11 闭环系统操纵响应Fig.11 Control response of closed-loop system
此外,从图10(c) ~图10(f)可以看出三输入模型的θ、q的振幅及˙q和nz的最大绝对值要明显小于二输入模型。 其原因在于:引入ΔR控制输入后,通过机翼在扑动过程中的扭转实时地调整机翼迎角,从而达到调整机翼产生的升力、阻力的大小和方向的目的,进而使得在扑动过程中全机的CL和Cm的振幅更小,最终达到减缓θ、q的振幅及˙q和nz的最大绝对值的效果。

图10 闭环状态量响应Fig.10 States response of closed-loop system
为对引入ΔR后的控制效果进行更有效评价,探索了评价指标的构建问题。 扑翼机飞行时的实际情况表明,θ振动过大会对空中投弹、侦查拍摄等任务造成不利影响,˙q和nz过大会使机体结构承受过大的弯矩和惯性力,从而造成结构疲劳。 因此,为了更清晰地表达减缓效果,提出式(10)所示的状态平缓度指标:

式中:κ1、κ2、κ3为归一化系数,取值分别为0.373 4、4.152 5 ×10-5、9.809 7;nz为法向过载。 仿真结果显示,二输入模型的状态平缓度指标为100.501 9,而三输入模型为83.450 7,减缓了17.05。
4 结 论
1) 鸽子飞行时常采用变频率和振幅模式来调控翅膀扑动、扭转以达到高效飞行的目的。 研究发现,定周期等振幅扑动翅膀条件下,仅靠尾巴偏转不能既实现高度的控制又实现速度的保持和控制,因此,需要引入机翼扑动角振幅作为控制输入来实现速度的保持,同时也有必要引入机翼扭转角振幅作为控制输入以进一步提升轨迹跟踪飞行的平稳性和高效性。
2) 基于Floquet 理论对仿鸽扑翼机线性时变周期系统模型展开了动稳定性分析,与开环时域仿真结果一致,表明了仿鸽扑翼机具有缓慢发散模态,从而指明了设计增稳和控制器的必要性。
3) 闭环仿真结果表明机翼扭转角振幅这一输入量的引入能显著提升轨迹跟踪过程的平滑性,使状态平缓度指标降低了17.05,验证了所建模型的有效性及模型输入维度增加带来的模型适应性。
