可变后掠翼联动驱动机构设计与尺寸综合
2023-01-12都显琛刘学翱董洋王辉何天宇王春洁
都显琛, 刘学翱, 董洋, 王辉, 何天宇, 王春洁
(北京航空航天大学 机械工程及自动化学院, 北京 100191)
可变后掠翼飞行器可通过改变其机翼后掠角,实现对飞行器临界马赫数、升力特性、阻力特性等性能的调节,从而在不同的飞行速度条件下,保持较好的飞行性能。
变后掠翼的关键技术之一是变后掠翼驱动的机构设计,传统的变后掠翼驱动机构通常采用平面四杆机构及其衍生机构[1],以平面四杆机构为基础进行设计与优化[2-3]。 平面四杆机构运动特性较为简单,但只可实现机翼后掠角的变化,无法在机翼后掠角变化的同时,令机翼做出其他动作。例如,蒙皮的一部分需要随机翼运动收拢或展开,使用传统后掠翼四杆驱动机构则需要额外添加驱动,会提高机构整体的复杂度。 基于平面复合连杆机构,提出一种联动驱动机构,能同时满足机翼和蒙皮的运动要求。 平面复合连杆机构相对于平面四杆机构,可以获得更加多样的运动特性,但其机构综合分析及可动性分析方法也更加复杂。 对于平面连杆机构的机构综合分析,常用方法为几何关系法、相对位移矩阵法、矢量方程法等,目标为解决机构综合中的函数生成综合[4]、位置生成综合[5-7]、轨迹生成综合3 大任务[8-11],Schreiber等[6]利用同伦法对典型Stephenson 机构进行了位置生成综合求解,周洪和邹慧君[10]对六杆机构双目标轨迹综合进行了分析求解。 对于平面连杆机构的可动性分析问题[12-15],张春等[12]针对一种平面复合连杆机构,利用几何方法与数学方法分别对该平面复合连杆机构进行了可动性分析;于红英和唐德威[15]推导了平面五杆机构的雅可比矩阵,并利用雅可比矩阵分析了机构的奇异轨迹。针对平面连杆机构的尺寸综合方法及可动性分析方法,学者们已经进行了许多研究。 而对于如何在机构尺寸综合求解的过程中,保证机构不产生可动性问题,相关研究还较少。
本文基于平面复合连杆机构,提出了一种可变后掠翼联动驱动机构,该机构可拆分为3 个平面连杆子机构,可通过单驱动同时实现机翼后掠角的改变及机翼部分蒙皮的展收。 利用矢量方程法,对机构进行机构综合分析,建立机构的矢量环路方程,并对机构可动性进行分析。 通过建立的机构矢量环路方程,对机构进行函数生成综合与运动生成综合相结合的尺寸综合设计求解,结合动力学分析软件与优化算法对机构可动性进行判断,获得了符合设计要求且满足可动性与尺寸约束要求的最优机构构型。
1 机构描述与分析
1.1 机构描述
变后掠翼机构运动简图与全局坐标系定义如图1 所示。 摇杆CBDE为飞行器机翼,构件FPG为需要展收的飞行器蒙皮,由P点指示其位置与转角。 摇杆CBDE绕C点转动实现变后掠翼动作,构件FPG执行蒙皮收拢与展开动作。
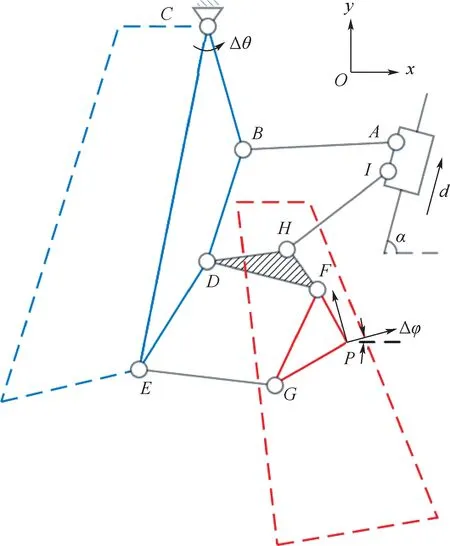
图1 机构简图Fig.1 Schematic diagram of mechanism
A-H均为转动副,该机构自由度计算式如下:
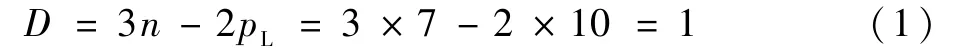
式中:n为机构中活动部件数;pL为机构中运动副数。 通过计算可知,该机构自由度为1,可通过滑块运动同时驱动摇杆CBDE及连杆FPG。 图1 中Δθ为摇杆CBDE相对初始机构初始位置转动角度,Δφ为蒙皮上点P相对初始位置的姿态变化角,d为滑块相对初始位置的位移,α为滑块的运动方向与水平方向夹角。
定义在该机构第j个状态(j=[0,1,…,n]),滑块相对初始位置位移为dj时,后掠翼CBDE转动角度为Δθj,Pj点位置为(xPj,yPj),姿态变化角为Δφj。 当j=0 时,变后掠翼驱动机构处于初始位置。 针对该机构,进行函数生成综合与运动生成综合相结合的机构综合分析。
1.2 机构综合约束的建立
矢量方程法是以矢量运算为基础的机构分析方法,普遍适用于机构的运动学分析,可用于解决机构综合问题。 利用矢量方程法,建立该机构的矢量环路方程。
将该平面复合连杆机构拆分为3 个子机构分别进行分析。 子机构简图如图2 所示,红色线条表示拆分得到的各子机构。 分别对子机构建立几何关系的矢量方程,得到机构整体的综合等式。
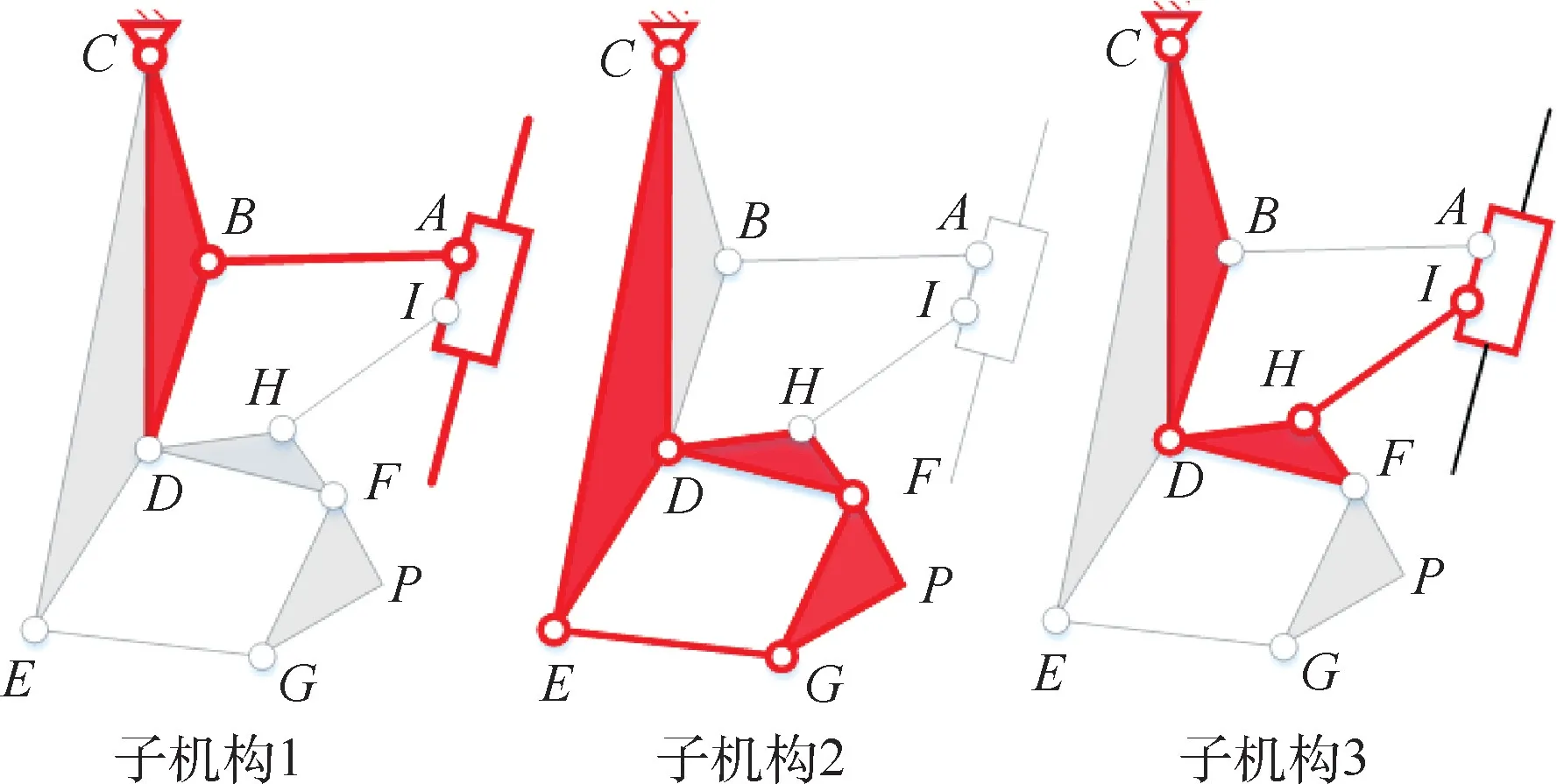
图2 子机构简图Fig.2 Schematic diagrams of sub-mechanisms
子机构1 为曲柄滑块机构,第j个状态矢量图如图3 所示。
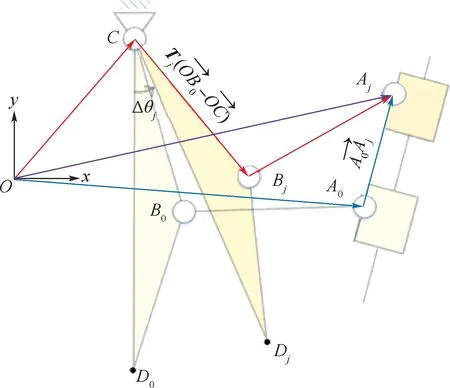
图3 子机构1 矢量图Fig.3 Vector diagram of sub-mechanism 1
根据矢量图,建立子机构1 的几何关系:

其中:Tj为旋转矩阵,表示为
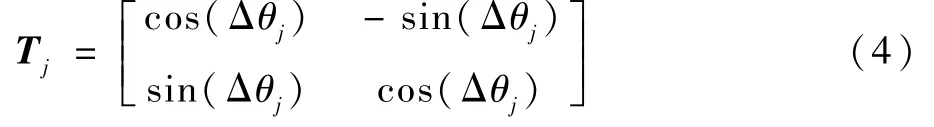
由机构运动状态,在机构的第j个状态,有式(5)成立:

AB杆长度不变,式(7)、式(8)联立即可建立滑块连杆机构的综合等式。

子机构2 矢量图如图4 所示。 根据图4 中,闭环ODFP及闭环OFGP的几何关系,可得
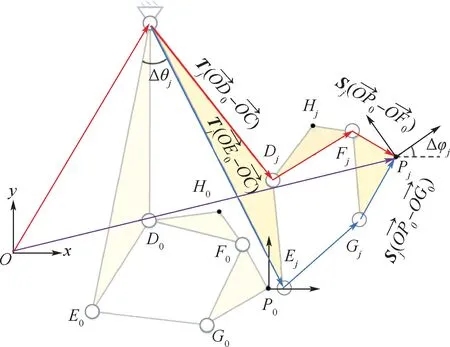
图4 子机构2 矢量图Fig.4 Vector diagram of sub-mechanism 2
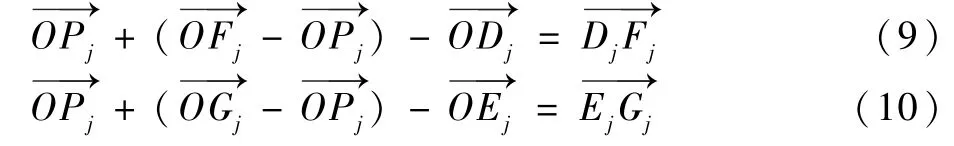
在机构运动过程中,DE杆随子机构1 中BC杆转动,可得
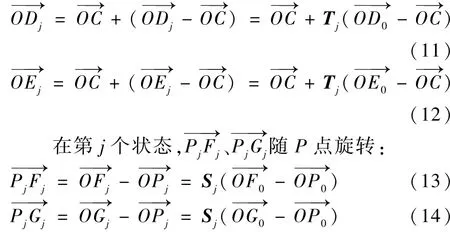
式中:Sj为P点姿态变化的旋转矩阵,表示为
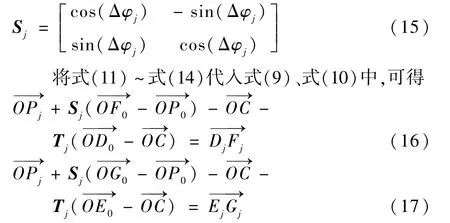
由FP、GP杆长度不变得

联立式(16) ~式(19),即可建立子机构2 的矢量环路方程。
子机构3 为五杆机构,其矢量图如图5 所示。
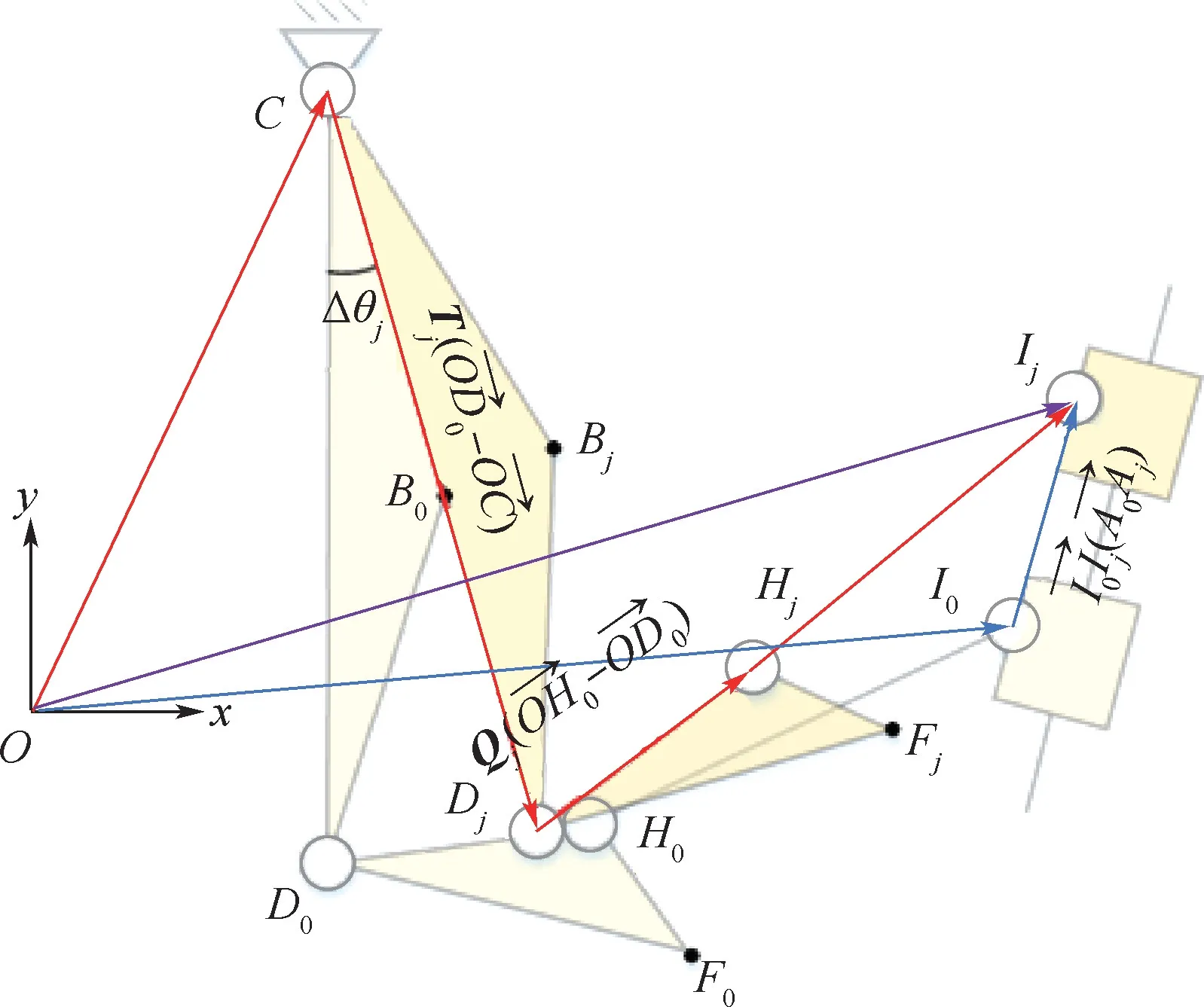
图5 子机构3 矢量图Fig.5 Vector diagram of sub-mechanism 3
根据图5 建立子机构3 的几何关系,如下:
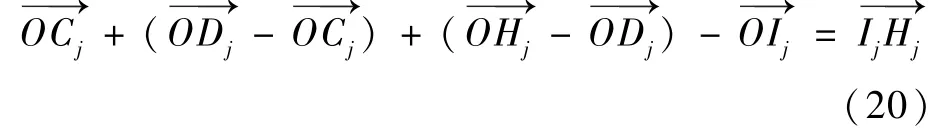
D0H0旋转至DjHj的旋转矩阵如下:
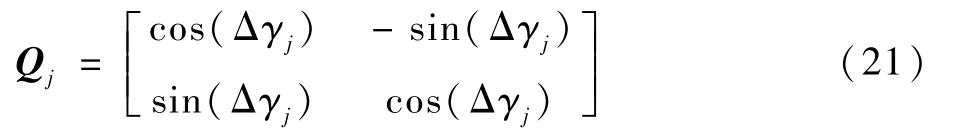
式中:Δγj为D0H0旋转角度。
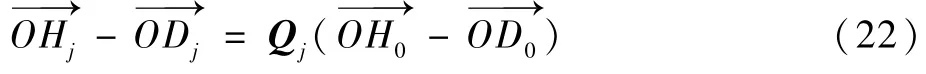
其中,构件DHF的运动与子机构2 的运动相关联,根据转角关系可建立子机构2、3 的运动耦合关系。 由构件DHF在子机构2 中的旋转可得
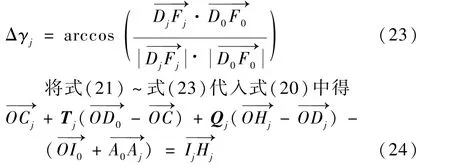
由IH杆长度不变,建立子机构3 的矢量环路方程为

由各子机构的几何关系, 综合式(8)、式(18)、式(19)、式(25),建立了可变后掠翼联动驱动机构的矢量环路方程。
2 机构可动性分析
2.1 机构奇异点分析
当机构雅可比矩阵奇异时,机构处于奇异点。 机构的奇异位形出现在雅可比矩阵行列式为0 或趋于∞处。 子机构1、2、3 中都可能出现奇异点,而任一子机构出现奇异都会导致整个机构出现奇异,故分别计算3 个子机构的雅可比行列式。
子机构1 闭环约束方程为
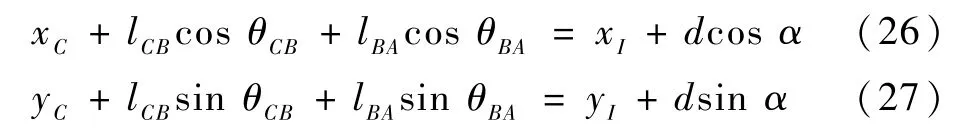
式中:lCB为C、B2点间杆件长度;θCB为C、B2点间杆件与水平方向夹角。
式(26)、式(27)两侧对时间求导可得
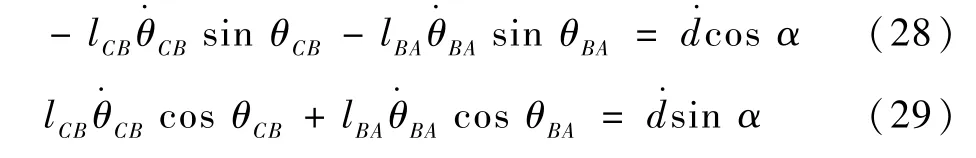
联立式(28)、式(29),得子机构1 的雅可比矩阵J1及其行列式:

由雅可比矩阵为零条件可得,子机构1 出现奇异点的条件为:θBA=θCB+mπ(m=0,1,…,n)时,正运动学出现奇异;θBA=α时,逆运动学出现奇异。
子机构2 闭环约束方程为
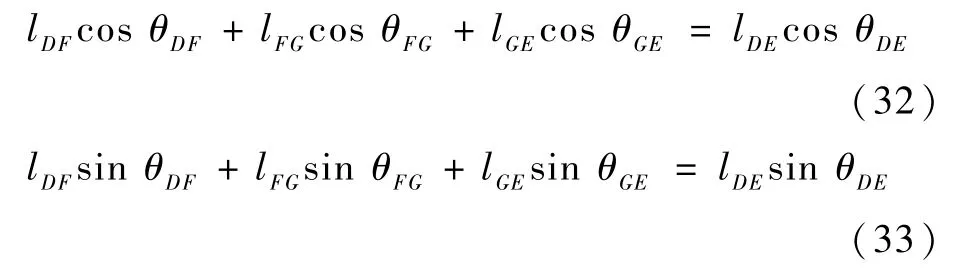
式(32)、式(33)两侧求导可得
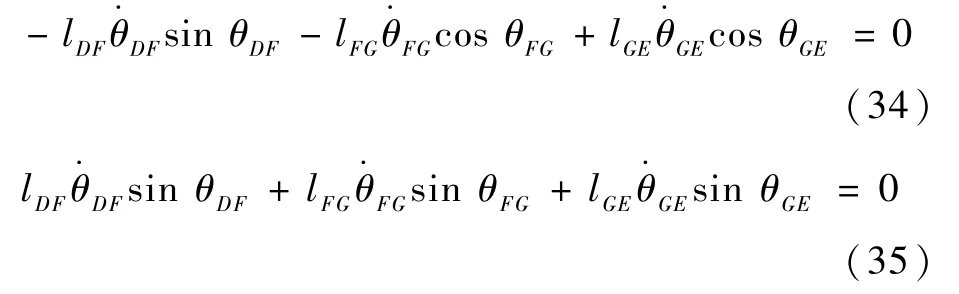
联立式(34)、式(35),得子机构2 的雅可比矩阵J2及其行列式:
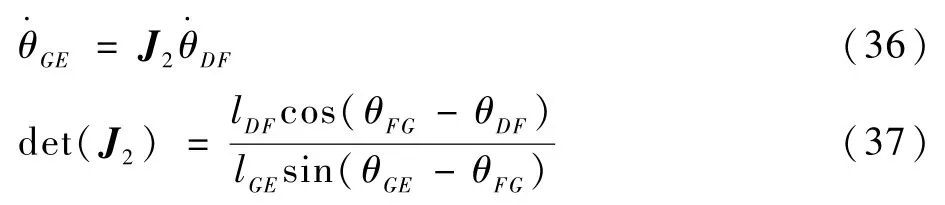
由雅可比矩阵为零条件可得,子机构2 出现奇异点的条件为:θGE=θFG+mπ(m=0,1,…,n)时,正运动学出现奇异;θFG=θDF+mπ(m= 0,1,…,n)时,逆运动学出现奇异。
子机构3 闭环约束方程为
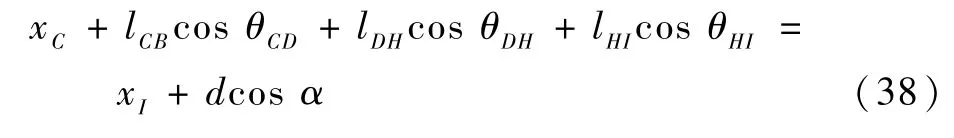
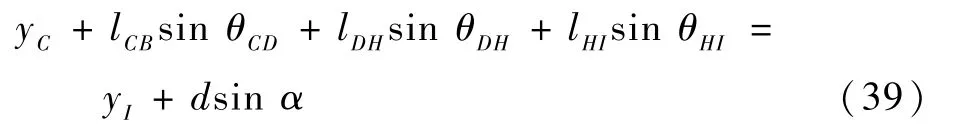
式中:θCD与滑块位移d在子机构1 中相关,f(d)为θCD与滑块位移d的映射关系:

将式(40)代入式(38)、式(39)中,并对时间求导可得
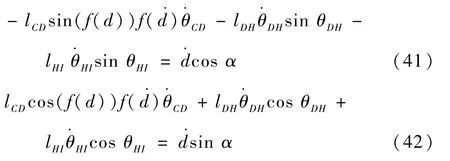
联立式(41)、式(42),得子机构3 的雅可比矩阵J3:

由雅可比矩阵为零条件可得,子机构3 出现奇异点的条件为:θHI=θDH+mπ(m=0,1…,n)时,正运动学出现奇异;逆运动学出现奇异位置,取决于子机构1 中θCD与滑块位移d的映射关系。
拆分得到的3 个子机构中,任一子机构出现奇异时,整个机构出现奇异。 在该机构的运动分析中,始终由滑块作为机构驱动,故只关注机构的正运动学奇异性。 根据分析可知,当A、B、C这3 点,D、H、I这3 点或E、G、F这3 点共线时,机构正运动学出现奇异。
2.2 机构可动性问题
平面连杆机构的可动性,是机构按照预期的运动方式依次通过若干位置的运动能力。 在该平面复合连杆机构中,影响机构可动性的因素主要为机构出现死点及机构运动分支的存在。
通过可变后掠翼机构奇异性分析可得,当机构正运动学出现奇异时,运动中出现死点的情况如图6 所示情况,当D、H、I点或E、G、F点在运动中处于同一直线时,机构出现死点。
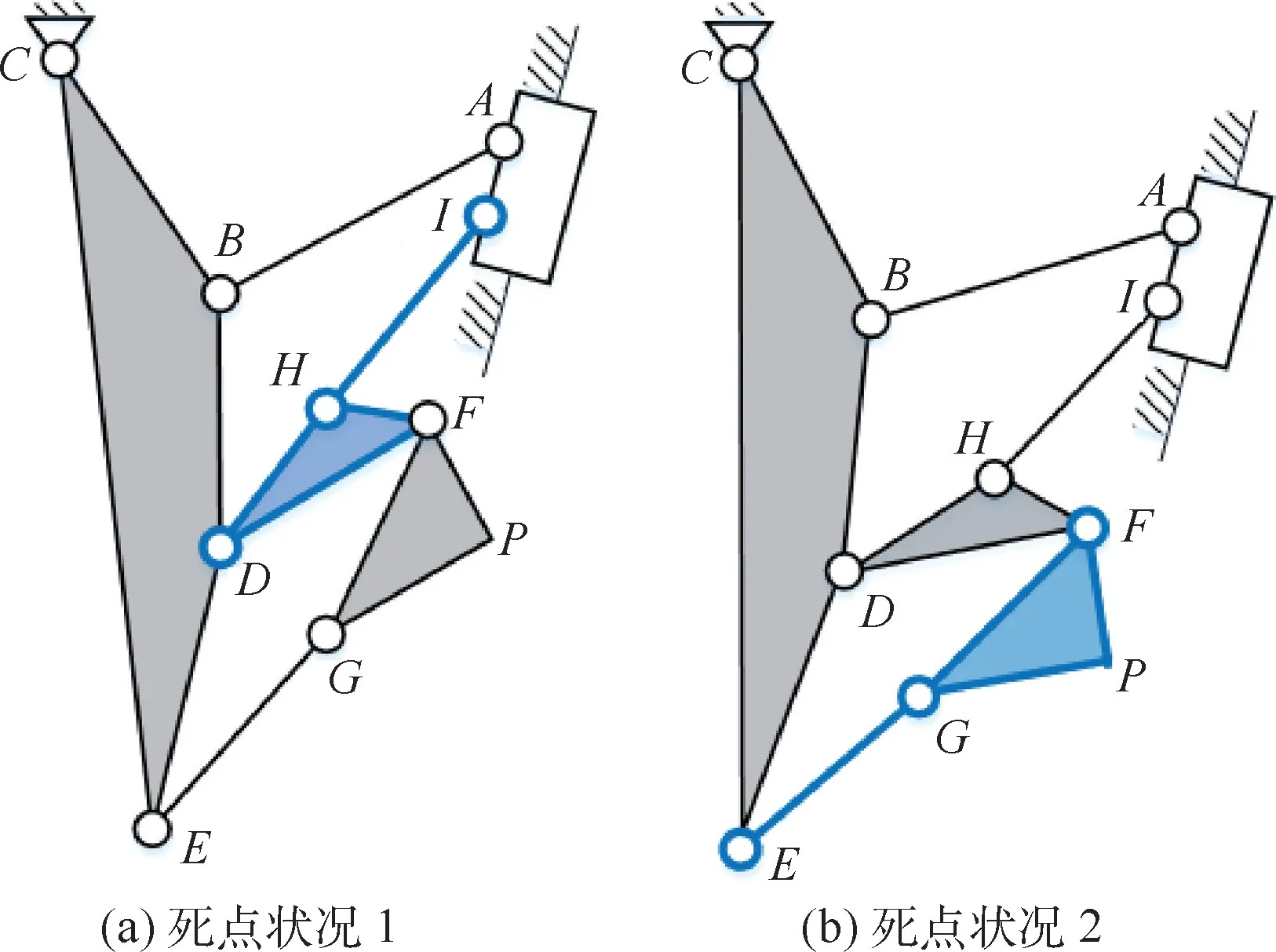
图6 机构死点Fig.6 Dead center of mechanism
由于回路分支的存在,导致可变后掠翼机构无法到达设计位置的情况。 如图7 所示,在同样机构尺寸的情况下,设计位置与实际位置不处于同一运动回路,导致机构无法到达设计位置,同样不满足机构的可动性需求。
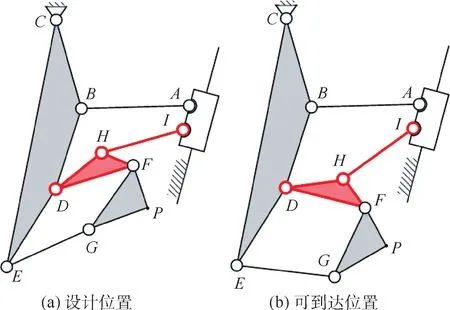
图7 机构运动分支Fig.7 Branch defect of mechanism
3 基于优化算法的机构综合求解
3.1 机构综合求解方法
由于可变后掠翼联动驱动机构较为复杂,在求解中难以通过解析方法给出机构出现死点和分支位置的判断依据。 针对该问题采用了一种基于机构综合方程,结合动力学仿真软件ADAMS 进行机构可动性判断,在铰链位置范围内,通过优化算法寻找机构最优解的方法。
单次迭代过程如图8 所示。 单次迭代中通过优化算法确定优化变量取值,结合机构综合等式进行求解,并且通过运动学分析进行可动性判断。
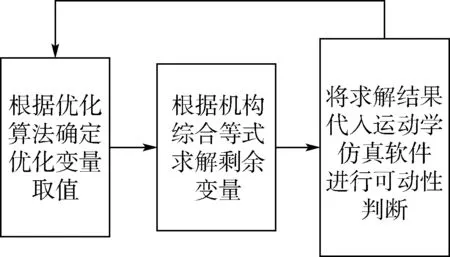
图8 单次迭代过程Fig.8 Single iteration process
3.2 目标函数与约束的建立
在可变后掠翼机构中,除保证机翼转角到位,还需要保证蒙皮运动中间位置合理。 以表1 中设计位置为例,位置2 为机构到位位置,位置1 为中间位置。

表1 设计位置Table 1 Target positions
机构中共19 个变量,分别为A-H点坐标(xA,yA) ~(xH,yH)及滑块运动方向与水平方向夹角α,根据3 个设计位置共可求解8 个变量,选择8个变量{xA,yA,xF,yF,xG,yG,yH,yI} 作为求解变量。
剩余11 个变量中,以B、E这2 点坐标及H、I这2 点横坐标为优化变量,固定C、D点坐标及滑块运动角度。 在机构设计中,由于可变后掠翼机构安装位置与空间的限制,优化变量范围与固定变量取值如下:

优化问题主要由目标函数和约束条件两部分组成。 本实例中目标函数为机构在初始状态的矩形包络面积,优化目标为使包络面积最小。 机构包络面积定义如下:
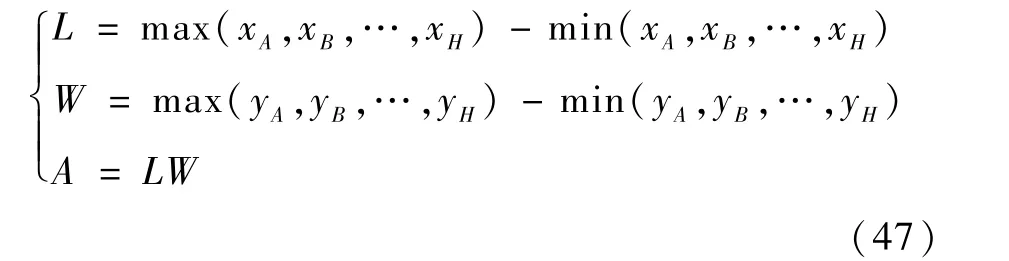
式中:L为机构初始状态的横向最大距离;W为纵向最大距离;A为包络面积。
约束为机构在运动中不出现死点,且设计位置处于实际运动回路,即机构可以完成运动行程,并到达设计位置1、2,约束等式为

3.3 优化结果及验证
使用Isight 软件中的pointer 算法进行优化,获得了机构在本次迭代中的最优解。 优化前后优化变量取值、机构运动情况及包络情况如表2 ~表4 所示。

表2 优化前后优化变量取值Table 2 Values of variables before and after optimization mm

表4 优化前后机构运动情况Table 4 Motion states before and after optimization
对求解得到的机构尺寸构型进行验证,机构尺寸构型及运动到位情况如图9 所示。

表3 优化前后求解变量取值Table 3 Values of the unknowns before and after optimization mm
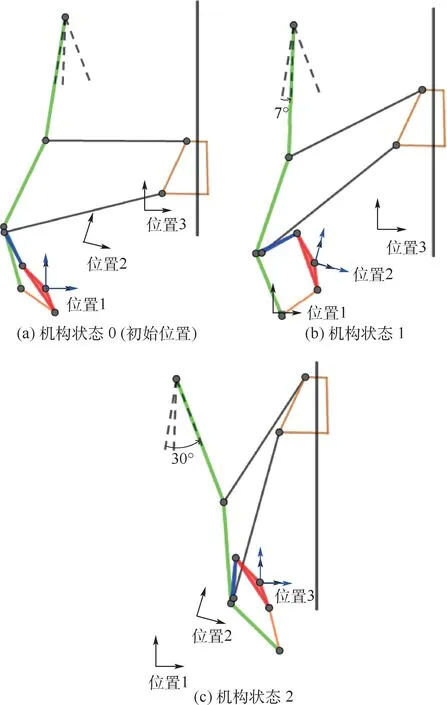
图9 运动到位情况Fig.9 States of movement
根据验证,求解得到的机构通过了设计转角与设计位置,满足机构功能需要。 通过所提方法,得到了符合可动性要求,且初始位置矩形包络相对初始设计更小的可变后掠翼联动驱动机构。
4 结 论
基于平面滑块连杆机构,设计了一种可同时实现机翼后掠角变化和蒙皮展收的可变后掠翼联动驱动机构,并对该机构进行了分析与优化。
1) 本文提出一种用于可变后掠翼机翼的联动驱动机构,基于平面复合连杆机构,实现了在单驱动条件下,同时完成变后掠翼与部分蒙皮展开与收拢。
2) 针对所提可变后掠翼联动驱动机构,对机构进行拆分,利用矢量方程法,建立了机构拆分后的各个子机构的矢量环路方程,并对机构的可动性进行分析。
3) 对于该机构运动生成综合与函数生成综合相结合的尺寸综合的求解,提出一种基于运动学分析软件与优化算法的求解方法,结合矢量环路方程,解决了尺寸综合任务中机构的可动性问题,获得了符合运动要求且包络较小的可变后掠翼机构尺寸构型。
