Tanabe 模型和Smith 热调节模型结合预测皮温效果分析
2023-01-12王涛张万欣李猛卜雪琴张宸王海亮
王涛, 张万欣,*, 李猛, 卜雪琴, 张宸, 王海亮
(1. 中国航天员科研训练中心人因工程重点实验室, 北京 100094; 2. 北京航空航天大学 航空科学与工程学院, 北京 100191)
热调节模型是人体内外传热的数学描述[1],其可对核心温度和皮肤温度等生理参数进行预测,为热感觉和热舒适评价模型提供输入条件,因此,热调节模型是热感觉和热舒适评价方法的组成部分[2]。 日常生活中人们经常处于各类室内环境中,了解人体对环境的热感觉,评价环境的热舒适程度是建筑暖通设计和节能的需要,由此促进了人体热模型的发展。
人体热调节模型始创于20 世纪初期,文献[3]指出,1911 年提出了一个经验模型把人体描述成一个节点与外环境传热。 1934 年Burton[4]创建了人体传热数学模型,模型中包括人体解剖结构和热调节控制方程。 这些发展初期的人体热模型无论是精度还是适用性都较差。 20 世纪60 ~90 年代,一些具有里程碑意义的模型相继出现,如Gagge 两节点模型[5]、文献[6]所提模型和Smith 多元模型[7]等,2000 年后模型的发展多是在以上经典模型的思路框架下对模型中受控系统和热调节系统进行的改进、完善和创新,并加快了模型应用研究。 2001 年Fiala 等[8]创建多节点模型,其受控系统模型把人体划分为15 个节段,共187 个节点,描述了人体与外界对流、辐射、汗液蒸发等多种传热形式,考虑了衣物热阻的影响,其在生理热调节模型的建立上是通过试验数据的回归分析获得的生理热调控模型,该模型可以预测稳态和瞬态下人体整体和局部的生理热响应。2001 年UC Berkeley 多节点模型[9-10]是以Stolwijk模型为基础建立起来的,其受控系统模型可以把人体划分为任意个节段,并考虑了身高、体重、肥胖和性别等个体生理和衣物穿着差异,模型将以上人因参数变量融合到人体生成器中,可以研究不同生理特征对人体热响应的影响,其在生理热调节模型的建立上主要用与设定点温度进行比较,完成反馈和控制,该模型可以预测瞬态和非均匀下人体整体和局部的生理热响应。 2002 年Tanabe 等[11]建立的多节点模型也是以文献[6]所提模型为基础,其受控系统模型把人体划分为16 个节段,每个节段分为4 层共64 个节点,第65 个节点定义为中心血液,其与64 个节点进行对流传热,人体与外界通过对流、辐射、汗液蒸发等形式进行热交换,在生理热调节模型的建立上主要用与设定点温度进行比较,完成反馈和控制,该模型可以预测瞬态和非均匀下人体整体和局部的生理热响应。 2016 年Lai 和Chen[12]建立的多节点模型允许在不同节段上设置衣物热阻,并在相邻节段间增设了血液传热模拟;2018 年Davoodi等[13]在Gagge 两节点模型上考虑体重、身高、性别、年龄和基础代谢等个体因素发展出了个体化热调节模型;2019 年Kang 等[14]创建的多节点模型在相邻节段间模拟了导热传热;2020 年范路[15]通过对大量文献研究指出每种人体热模型都有其适用范围,需要根据实际应用加以修正,今后模型的改进将集中在血液模型、服装模型、个体差异和特定环境模型的改进上。 人体热模型的应用主要体现在热舒适[16-19]、暖通[20]、医疗[21]、特种服装[22]和暖体假人[23-24]等领域。
从经验模型到两节点模型,再到多元模型是一个由简单到复杂的发展过程。 模型越复杂对人体划分得越细致,越适合描述非均匀环境下的人体热响应,但同时模型使用难度也越大,对计算机的运算和存储能力要求也越高。 随着计算机技术的普及应用,近30 年来人体热模型得到快速发展。Tanabe[11]模型、Fiala[8]模型和Berkeley 模型[9-10]等都是较为成功的模型。 尽管如此,目前用于生理参数预测的人体热模型还不能应用在热舒适评价的国际标准中。 这是因为模型没有统一公认的验证规范,研究文献中提供的试验验证方法和数据针对性强,无普适性。 这种状况使得模型预测精度和可靠性受到质疑[25]。 因此,现阶段人体热模型距离成熟应用仍有较大距离,还需要进一步的理论创新研究来夯实基础和试验研究积累数据。
本文创建的人体热调节模型在受控系统上采纳了Tanabe[11]模型,按生理自然节段把人体分为65 个传热节点,每个节点的传热采用Pennes 生物热方程,从传热学角度看Tanabe 模型对人体受控系统的划分更直观、简便、合理,抓住了人体内部传热的主要特征。 但其在热调节控制系统模型上采用与设定点温度进行比较反馈控制,该方法简单,个体差异对设定点温度值影响大,反映到模型预测上就是可靠性不高,相比之下,Smith 多元模型中的生理热调节模型是建立在大量人体解剖和生理数据基础上,热调节模型中的各类参数有其实际物理意义,更具客观性,更能描述人体生理热调节的客观规律。 因此,采用这2 种模型的组合可以有助于提高人体热调节模型的预测水平和可靠性,在学术和应用2 个方面体现出一定价值。2 种模型的组合在本文设定工况下对人体皮肤温度的预测和试验结果吻合度较高。
1 人体热调节模型
人体热调节模型可以分为受控系统模型和热调节控制系统模型2 部分。 受控系统模型是描述各层肌体组织、血液循环系统、呼吸系统和皮肤层与外界的传热;热调节控制系统模型用于描述人体应对外环境变化时肌体产生的热调节生理功能,包含血液系统输血量控制,皮肤血管舒缩引起的血流量变化控制,汗液分泌变化引起的蒸发散热控制,寒颤引起的肌肉层代谢产热控制。
1.1 受控系统模型
模型中的受控系统是从传热学角度对复杂人体组织的简化划分[11]。 依据人体结构特点将人体划分为头、胸、背、腹、上臂、下臂、手、大腿、小腿、足共16 个节段(下文用字母i∈[1,16]来指代身体各节段),每个节段沿径向分成4 层:核心层、肌肉层、脂肪层和皮肤层(下文用字母j∈[1,4]来指代各组织层),外加一个中心血池,这样人体就由65 节点构成。 如图1 所示,各层组织间通过导热形式传递热量,组织层与血液循环系统发生的传热被简化成与中心血池的传热,皮肤层与外环境间通过对流、辐射、蒸发和呼吸进行热交换,其中呼吸传热仅限头部和胸部。
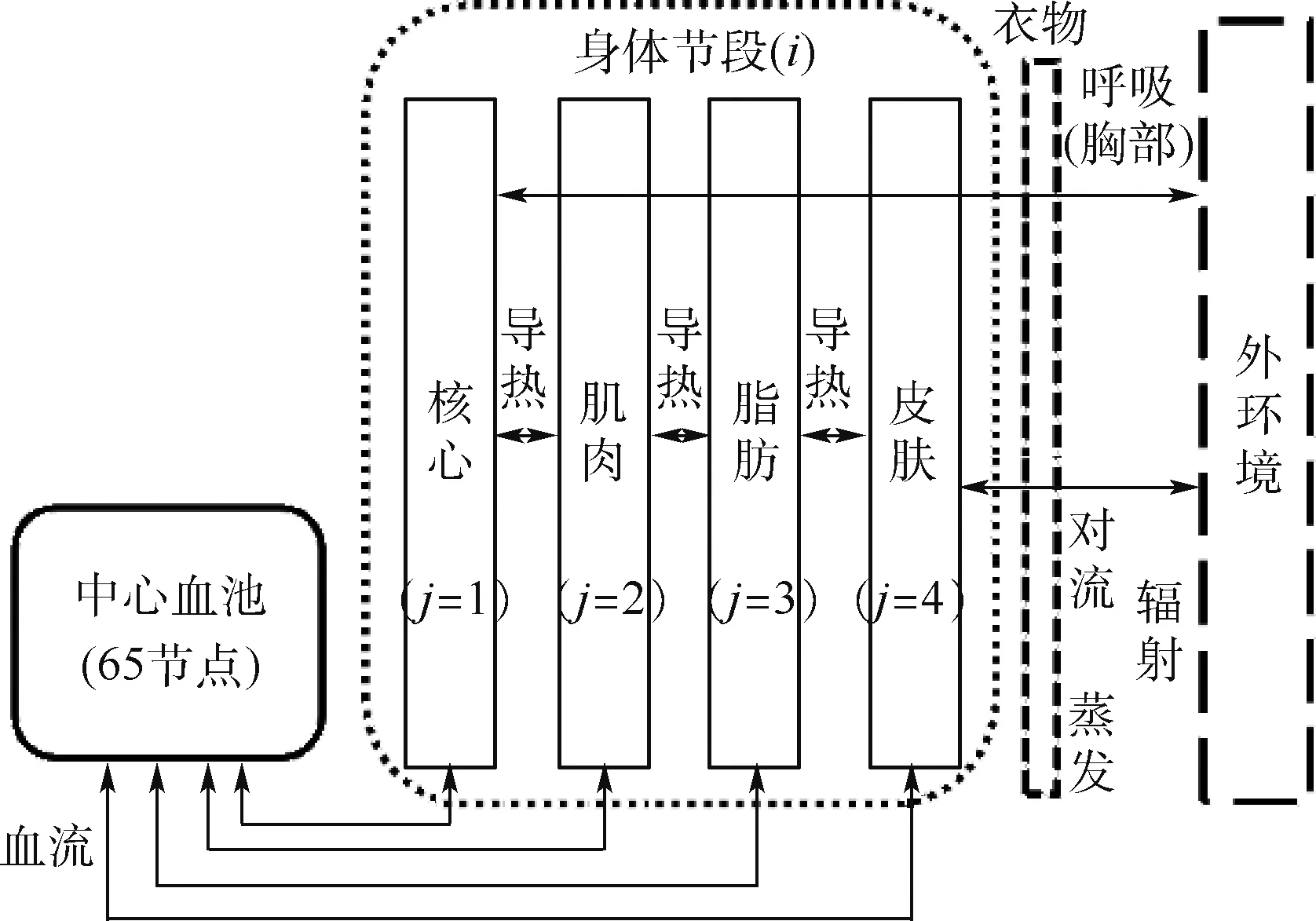
图1 人体受控系统传热原理Fig.1 Heat transfer schematic diagram of human passive system
利用Pennes 生物热方程对4 个组织层和中心血池建立能量平衡方程:
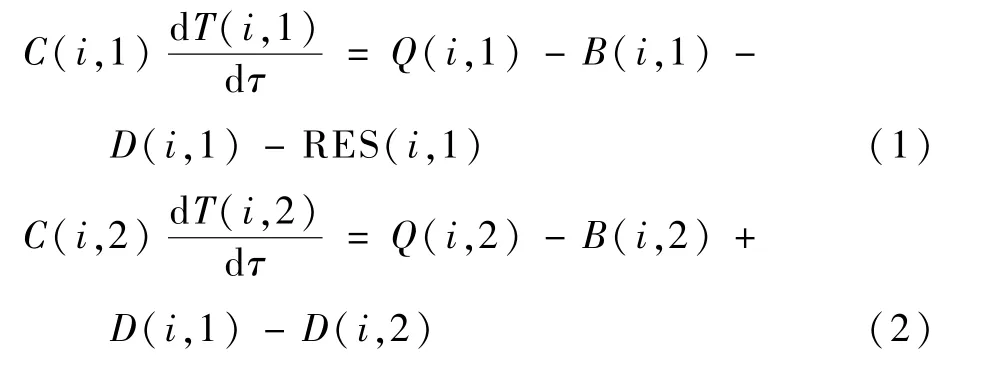

式中:C为人体组织比热容[11],(Wh)/℃;T为人体各层温度,℃;τ为时间,s;Q为代谢产热,W;B为血流传热,W;D为组织层间的导热,W;RES 为呼吸传热,W;QT为皮肤层与外界的显热传热,W;E为皮肤层与外界的潜热传热,W。1.1.1 代谢产热计算
代谢产热Q(i,j)计算如下:
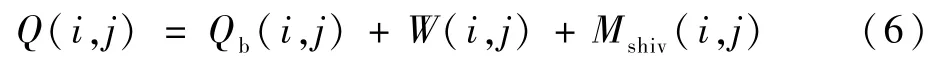
式中:Qb(i,j)为各组织层节点的基础代谢率[11];W(i,j)为对外做功产热;Mshiv(i,j)为寒颤产热。做功产热和寒颤产热只发生在肌肉层(即j=2),其他层为0。
人体对外做功计算如下:
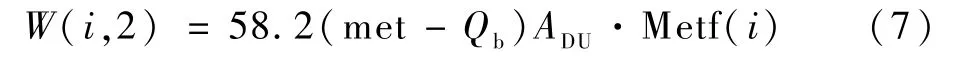
式中: met 为代谢当量( metabolic equivalent,MET),是一种表示运动强度的重要指标,1 met 定义为一个健康成年人静坐保持舒适状态时的新陈代谢率,约为58.15 W/m2;Qb为基础代谢率,是人体节段各组织层节点基础代谢的总和,约为0.778 met;Metf(i)[11]为对外做功引起的人体肌肉层产热在每个节段上的分配系数;ADU为人体表面积,由Du Bois 公式计算,表示为

式中:W为人体体重,kg;H为人体身高,m。
1.1.2 血流传热计算
血流传热B(i,j)是中心血池与各组织层间的热交换,其计算式如下:
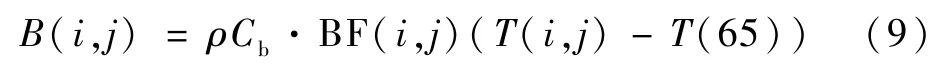
式中:ρCb为血液的体积比热[11],ρ为密度,Cb为比热;T(65)为中心血池温度;BF(i,j)为血流量,核心层、肌肉层和脂肪层血流量,其计算式为
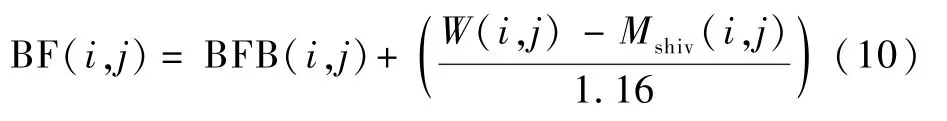
其中:BFB(i,j)为基础血流;式(10)等号右边第2项为代谢产热引起的血流增加量[11]。
1.1.3 组织导热计算
相邻组织层间的导热传热计算如下:
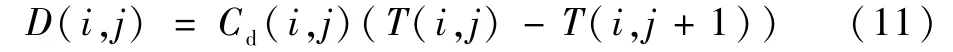
式中:Cd(i,j)为不同节段组织层的导热系数[11]。1.1.4 呼吸散热计算
人体的呼吸散热发生在头、胸部的核心层,即节点(1,1)和(2,1)处,RES(i,j)可表示为
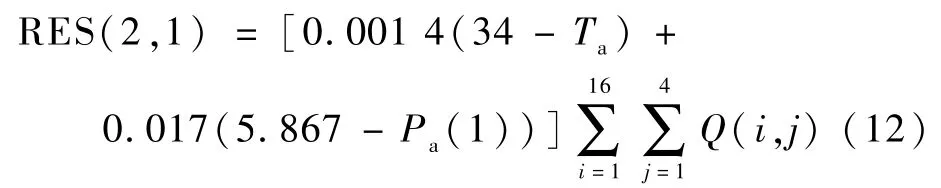
式中:Ta为环境温度,℃;Pa(1)为水蒸气压力,kPa。1.1.5 皮肤层与外界传热计算
皮肤层与外界散热有两部分组成:显热散热QT(i,4)和蒸发散热E(i,4),计算如下:
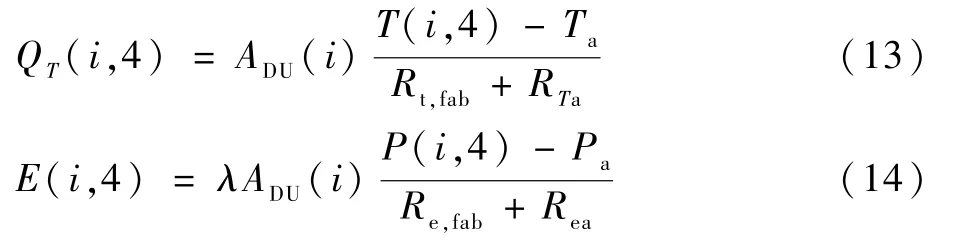
式中:λ为水的蒸发潜热,取33 ℃对应值2 422 kJ/kg;ADU(i)为节段i的体表面积[11];Ta为环境温度;P(i,4)和Pa分别为皮肤表面和环境水蒸气分压力,Pa;Rt,fab和Re,fab分别为衣物的热阻和湿阻,单位 分 别 为(m2K)/W 和(m2Pa)/W;RTa和Rea分 别为皮肤外表面空气层的热阻和水汽阻力,单位分别为(m2K)/W 和(m2Pa)/W,计算式为[26]
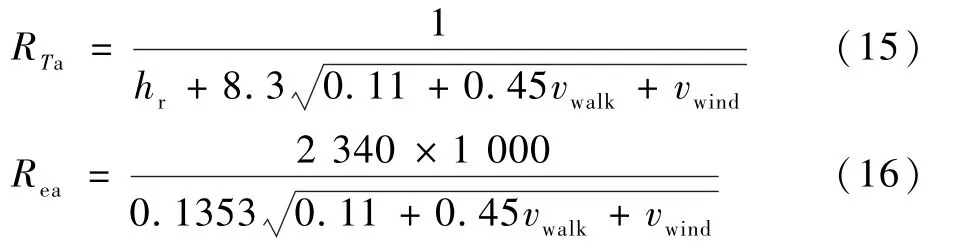
其中:hr为辐射传热系数,取5.0 W/(m2K);vwalk和vwind分别为步行速度和环境风速,m/s。
1.1.6 初始与边界条件
边界条件有环境温度、环境水蒸气分压力、风速、衣物热阻和湿阻等,均可通过试验测量。 核心层、肌肉层、脂肪层的初始温度参考文献[21]中热中性状态下的设定值,皮肤层的初始温度由试验值给出。
皮肤层水蒸气分压力P(i,4)和人体出汗率相关。 根据Umeno[27]的建议,人体皮肤表面汗液的聚集量不会超过35 g/m2的极限值,如有超出部分将会从皮肤上滴落或被内层衣物吸湿带走。在皮肤上的汗液聚集小于35 g/m2时,汗液聚集量等于出汗率加无感出汗减去汗液蒸发量,如下[28]:
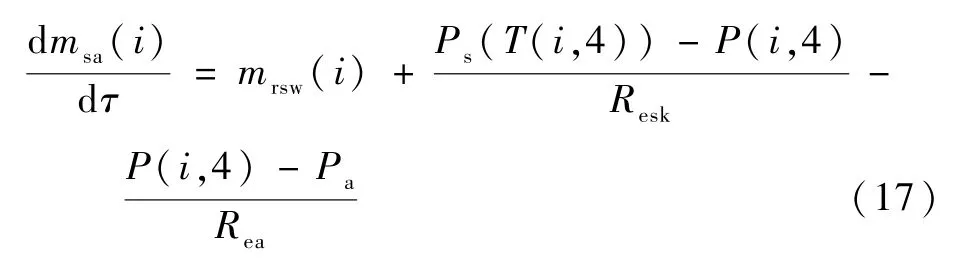
式中:msa(i)为第i节段皮肤层汗液聚集量,kg/m2;mrsw(i)为第i节段的出汗率,kg/(m2s);Resk为皮肤水蒸气阻力,(m2Pas)/kg;Ps(T)为环境温度Ta下的皮肤层饱和水蒸气分气压,Pa,计算式为

人体皮肤上出现汗液聚集时,皮肤表层的水气压力P(i,4)等于温度T(i,4)下的饱和水蒸气压力,在没有汗液聚集时,可由式(17)推导计算。由此P(i,4)计算如下:

1.2 热调节控制系统模型
热调节控制系统[7]原理如图2 所示。 人体皮肤层的温度感受器反馈信号与体温基准输入信号的偏差作为体温调节中枢的控制信号,控制调节肌肉寒颤、汗液分泌、血管舒缩或运动代谢来消除身体的冷热应激,维持人体核心体温和平均皮肤温度处于正常工作范围。
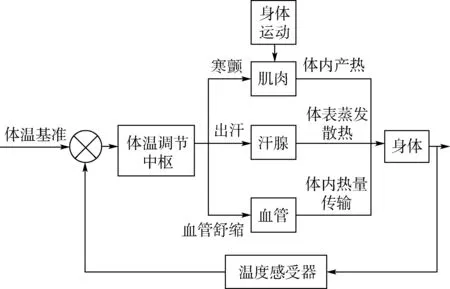
图2 人体热调节控制系统原理Fig.2 Schematic diagram of human thermoregulatory control system
人体热调节控制方程涵盖血管舒缩引起热量输送控制、汗液散热控制和肌肉代谢产热控制,反映了人体随环境改变的自适应调节功能特点,是人体热模型的重要组成部分。 本文采用Smith[7]基于试验数据提出的热调节控制系统模型。 模型中的控制变量为核心温度Tcore和平均皮肤温度Tskin,核心温度取中心血池温度T(65),平均皮肤温度计算如下:
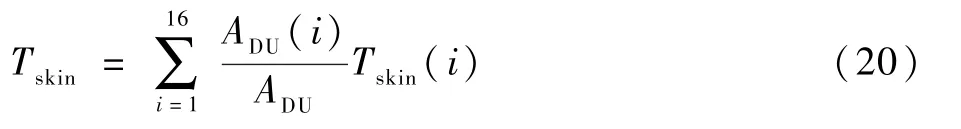
1.2.1 皮肤层血流量控制
皮肤层血管收缩时的血流量控制BFsk,con(i)计算如下:
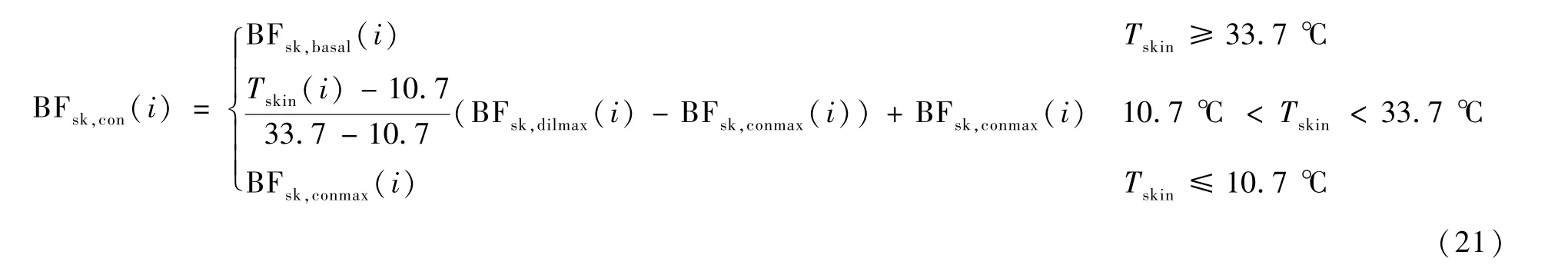
式中:BFsk,basal(i)为i节段皮肤层基础血流量[7];BFsk,conmax(i)为i节段皮肤血管最大收缩状态下的血流量[7]。
皮肤层血管舒张时的血流量控制BFsk,dil(i)为
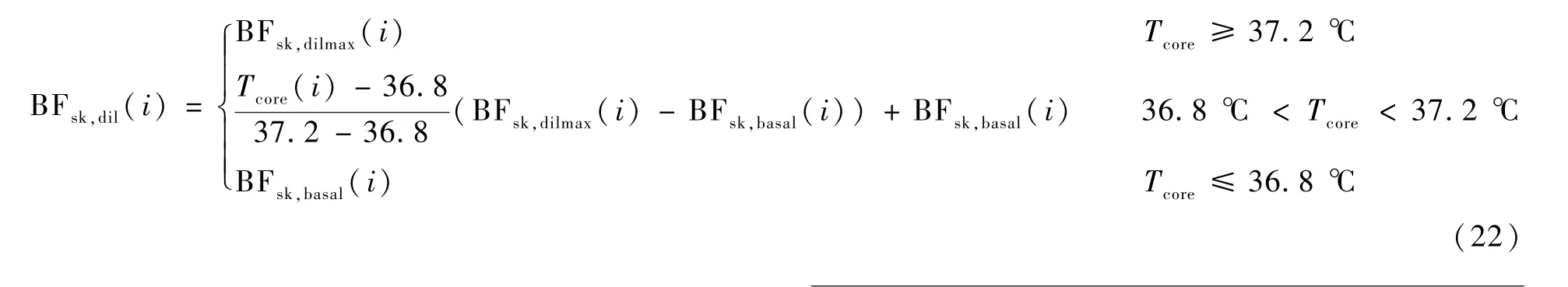
式中:BFsk,dilmax(i)为i节段皮肤血管最大舒张状态下的血流量[7]。
人体各节段皮肤层血流量计算如下:
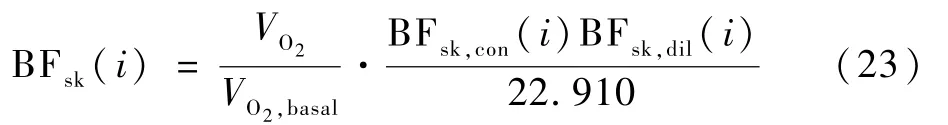
式中:等号右边第1 部分为人体耗氧量与热中性状态下耗氧量的比值,这说明血流量与人体运动耗氧成比例;VO2和VO2,basal分别为实时耗氧量体积和热中性状态下耗氧量体积,计算式为
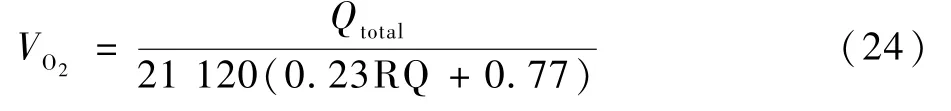
其中:Qtotal为总代谢率;RQ 为呼吸熵,定义为人体呼出二氧化碳体积流率与吸入氧气体积流率的比值,热中性状态下其值约为0.77。1.2.2 出汗率控制
核心温度Tcore超过了出汗阈值或37.1 ℃,人体会发生出汗现象。 出汗阈值Tsweat为平均皮肤温度Tskin的函数,计算如下:

人体出汗率最大值不超过0. 193 3 g/s。 整个人体出汗率msw,计算如下:
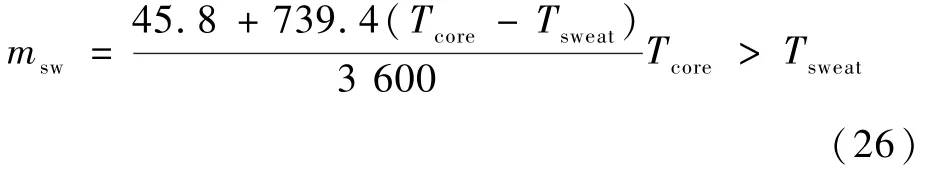
人体各节段的出汗率mrsw(i) (单位为kg/(s·m2)),计算如下:
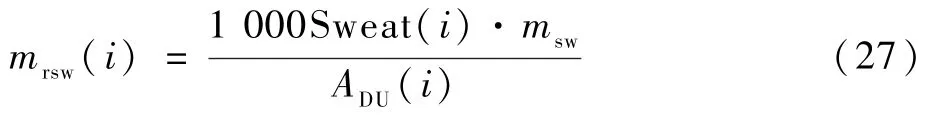
式中:Sweat(i)为每个节段出汗率的权重系数,是身体节段的汗腺数量与整个身体汗腺数量的比值[11]。
1.2.3 寒颤代谢产热控制
平均皮肤温度低于寒颤阈值Tshiv,则身体会发生寒颤现象,但当核心温度Tcore等于或高于37.1 ℃时,无论平均皮肤温度是多少,身体都不会发生寒颤。 人体发生寒颤的平均皮肤温度阈值Tshiv计算如下:
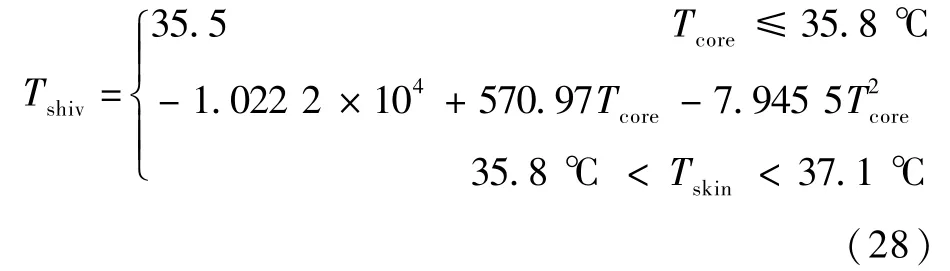
寒颤代谢率Mshiv计算如下:
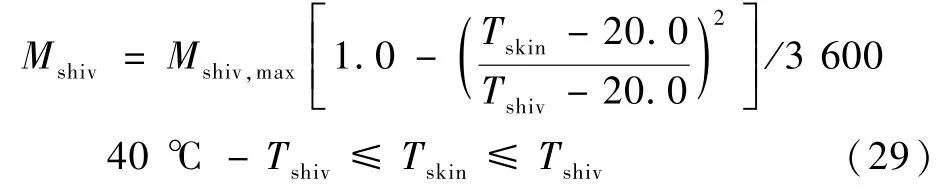
式中:Mshiv,max为寒颤引起的肌肉层最大代谢产热率,是核心温度的函数,计算式为
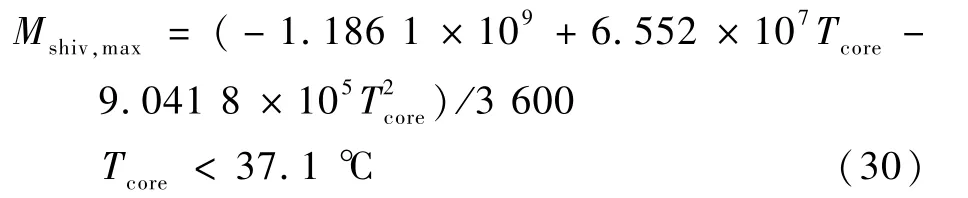
人体各节段肌肉层寒颤代谢产热率Mshiv(i,2)的计算需要引入寒颤加权系数Shiv(i)[11],该系数是将寒颤代谢Mshiv分配到身体每一节段的肌肉层中。 各节段肌肉层寒颤代谢产热计算如下:
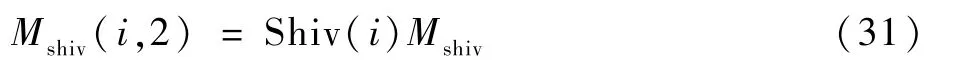
2 试验设计
考虑到在空调环境中的室内运动日益成为人们快节奏生活的选择,试验设计对此种情况设置了环境参数、运动工况,并对试验误差进行分析。
2.1 环境参数设置
根据常规室内空调环境,试验设定的环境温度、湿度、风速如表1 所示。 室内运动时穿着连体内衣,衣物整体热阻和湿阻的测定值如表1所示。

表1 环境参数汇总Table 1 Environmental parameters
为保障环境参数的一致性,受试者进入恒温舱完成上肢运动代谢流程,在此过程中采集人体皮肤温度等参数,试验现场照片如图3 所示。

图3 试验现场受试者做功照片Fig.3 Photo of a subject working at test site
2.2 运动工况设置
运动工况依据代谢量大小涵盖低强度活动量、中等强度活动量和高强度活动量。 低强度活动量下受试者做简单的上肢运动,中等和高强度活动量下受试者操作上肢功率计对外做功。 做功代谢量级、做功时间和间歇期的设定值依据GB/T 18048—2008[29]。 运动设置对应人体代谢产热量水平和运动工况信息如表2 所示。
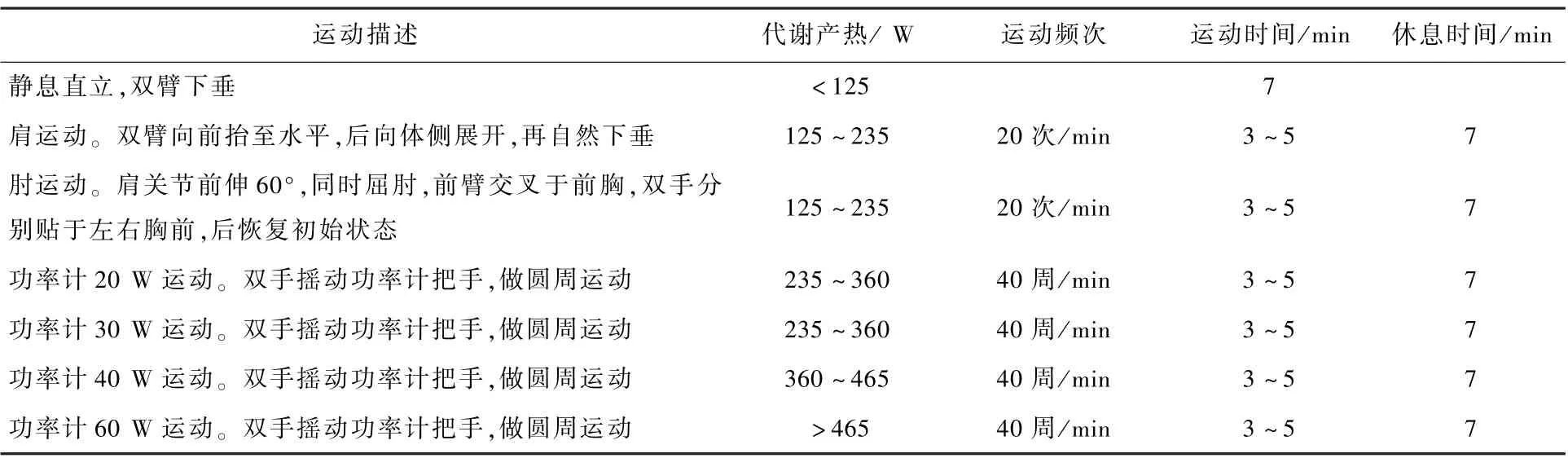
表2 运动工况设置Table 2 Motion settings
2.3 误差分析
试验测量的物理量有温度、湿度、流量、风速、质量和代谢量,相应的测量设备及精度信息如表3所示。肺功能仪用于实时采集人体吸入氧气和呼出二氧化碳的体积流量,以此计算人体代谢产热。计算方法如下:根据式(32)中的独立测量参数:氧气体积流量、二氧化碳体积流量、人体质量和人体身高,可以得到人体代谢产热测量误差,计算如下:

表3 试验设备信息汇总Table 3 Experimental equipment
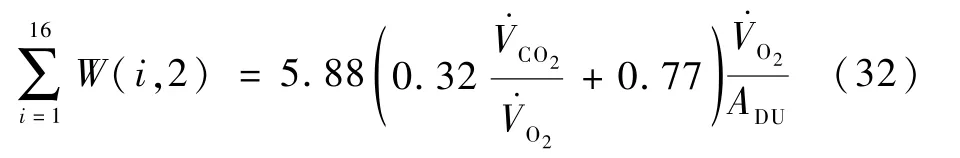
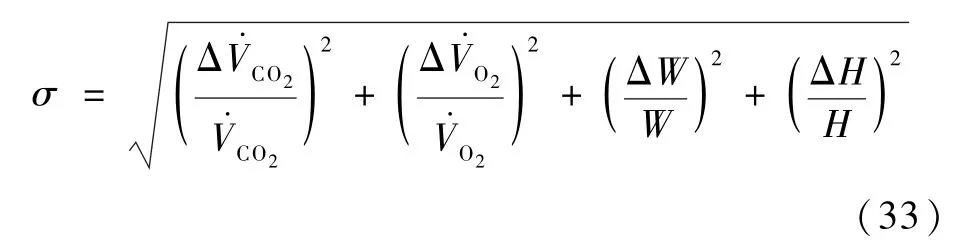
3 结果与分析
3.1 工况设置
受试者4 名,个人详细信息如表4 所示。
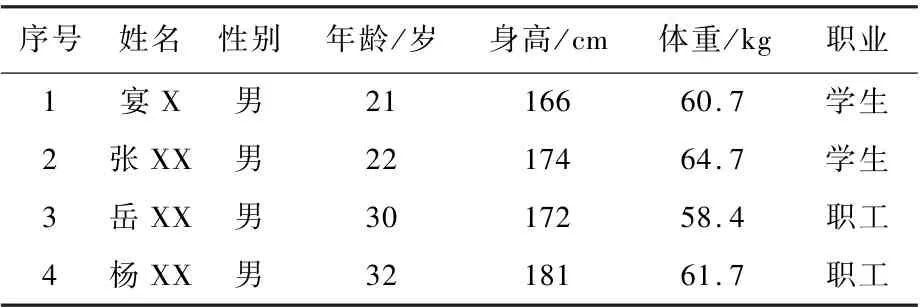
表4 受试者信息Table 4 Profile of subjects
试验中,受试者皮肤上贴附温湿度传感器,按规定着装后进入恒温室静坐1 h,恒温室温度设置为25 ℃,湿度为50%,风速为0(按0. 2 m/s 取值),在此过程中采集热中性状态下皮肤温度等生理参数,而后受试者如图4 所示,依次进行静立、肩运动、肘运动和操作上肢功率计对外20,30,40,60 W 做功。 受试者完成每一项运动用时4 min 左右,而后站立静息7 min,运动全程记录人体皮肤温度和外环境参数,试验中环境温度为25.6 ℃,大气相对湿度为54%。 人体周围风速为0.7 m/s,大气压强为98.6 kPa。
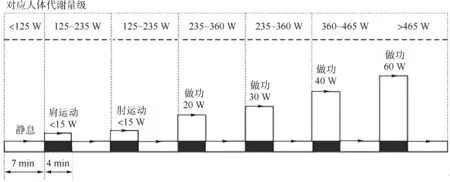
图4 人体运动做功流程Fig.4 Flow diagram of work by body movement
3.2 试验结果
图5 ~图8 为4 名受试者运动过程中各节段皮肤温度模拟计算值与试验值的对比分析。
图5(a)和图5(b)分别为受试者1 和2 与受试者3 和4 平均皮肤温度曲线和代谢产热曲线。随着对外做功负荷的增加,代谢产热随之升高,平均皮肤温度逐渐上升。 受试者1 ~4 的平均皮肤温度分别约为33.3 ℃、33 ℃、33.5 ℃和32.7 ℃。代谢产热曲线显示运动时人体产热增加,休息时下降。 在做功60 W 时,受试者1 和2 达到代谢产热约为6 met,受试者3 和4 达到代谢产热约为3 met,代谢产热的差别可能与年龄因素有关。4 名受试者平均皮温的仿真值与试验值最大误差小于0.7 ℃。 图6 为头部皮肤温度变化曲线。 曲线显示整个运动过程中,头部皮肤温度无明显变化,只在对外做功60 W 时略有增加。 这是因为头部不参与做功,其上汗腺分布密集,汗液的潜热散热可及时将热量散发到环境中。 4 名受试者头部皮肤温度仿真值与试验值最大误差均小于0.5 ℃。
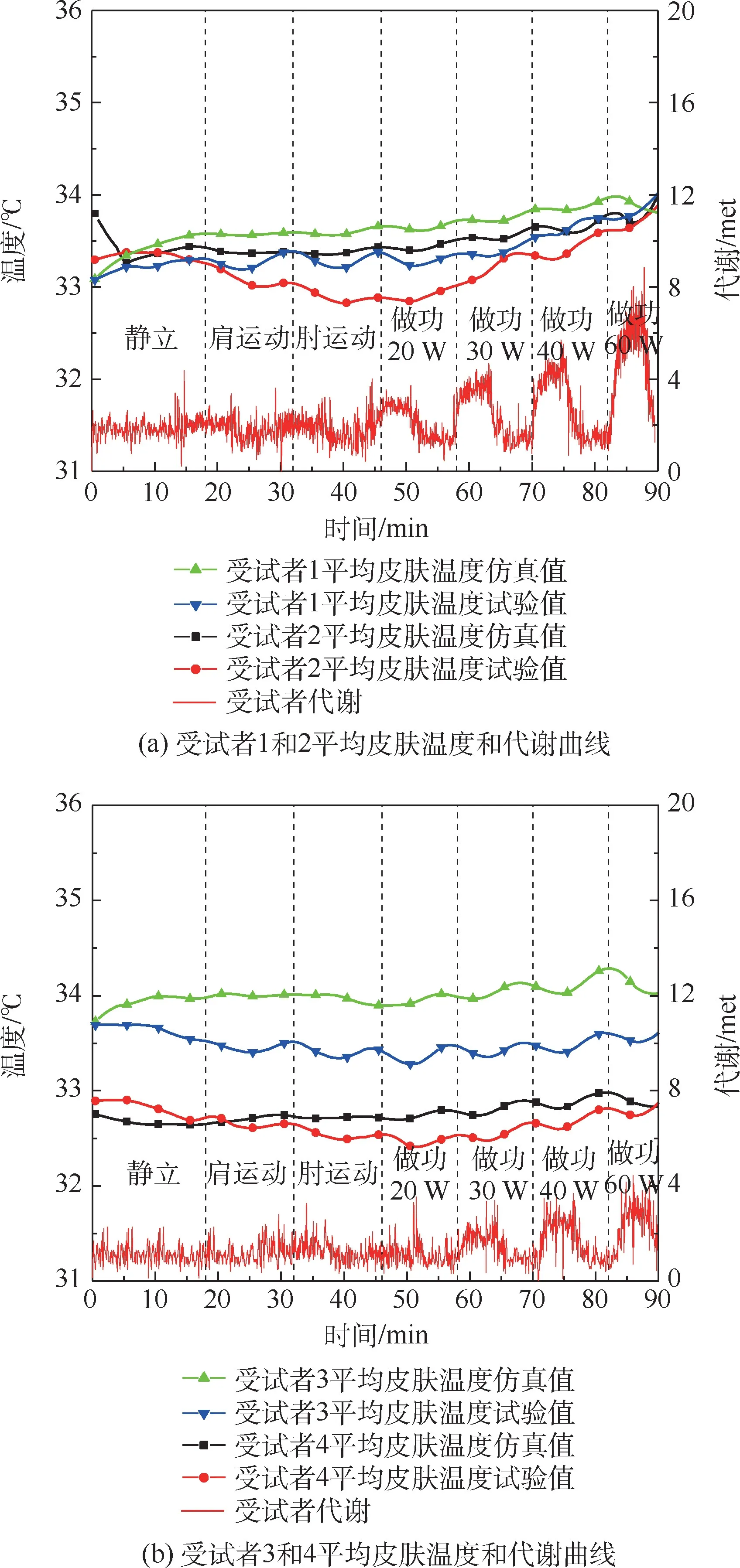
图5 平均皮肤温度曲线Fig.5 Mean skin temperature curves of bodies

图6 头部皮肤温度曲线Fig.6 Skin temperature curves of heads
图7 为背部皮肤温度曲线。 背部皮肤温度随上肢做功增加呈现上升趋势,这是因为背部肌肉群对外做功,引起背部皮肤温度升高。 在对外做功40 W 和60 W 的休息期间,受试者1 ~3 温度迅速上升形成波峰说明背部肌肉群中的代谢产热在做功完成后休息期间才传递到皮肤层,这揭示了人体组织传热具有滞后性。 受试者4 温度较为平缓,是因为出汗降低了皮肤温度。 4 名受试者背部皮肤温度仿真值与试验值最大误差小于0.6 ℃。

图7 背部皮肤温度曲线Fig.7 Skin temperature curves of backs
图8 为胸部皮肤温度曲线。 胸部皮肤温度曲线随着做功量增加呈现缓慢上升趋势,说明胸部肌肉层代谢产热与皮肤层对外散热基本保持了平衡。 但在60 W 做功休息期间温度有较明显上升,是由于60 W 做功时胸部肌肉层代谢产热速率显著大于皮肤层散热速率,又因为人体组织传热的滞后性使得皮温的迅速增加出现在60 W 做功后。 4 名受试者胸部皮肤温度仿真值与试验值最大误差小于0.7 ℃。
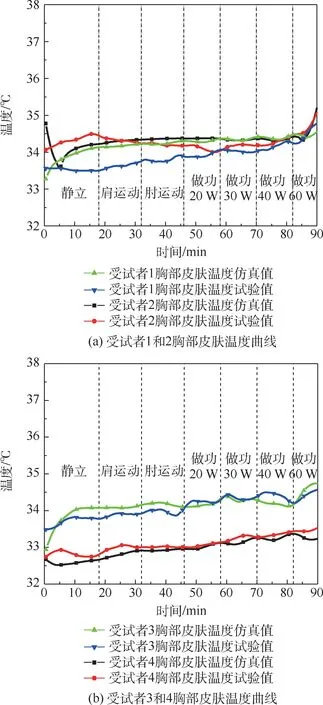
图8 胸部皮肤温度曲线Fig.8 Skin temperature curves of chests
图9 为上臂温度曲线。 上臂肌肉做功大,皮肤温度上升显著。 上臂皮肤温度曲线有明显的周期性波动—即在每个做功周期内,皮肤温度先下降后升高(运动时下降,休息时升高),这是做功和停歇的周期性活动引起代谢和对流散热变化而导致皮温的周期性改变:运动时上臂与空气间有较大的相对运动,空气的对流传热大,皮温下降;休息时对流散热小,同时因人体传热的滞后性使得做功的代谢产热休息期间释放到皮肤表面引起皮温增加。 4 名受试者1 号和2 号上臂皮肤温度仿真值与试验值最大误差均小于0.8 ℃。
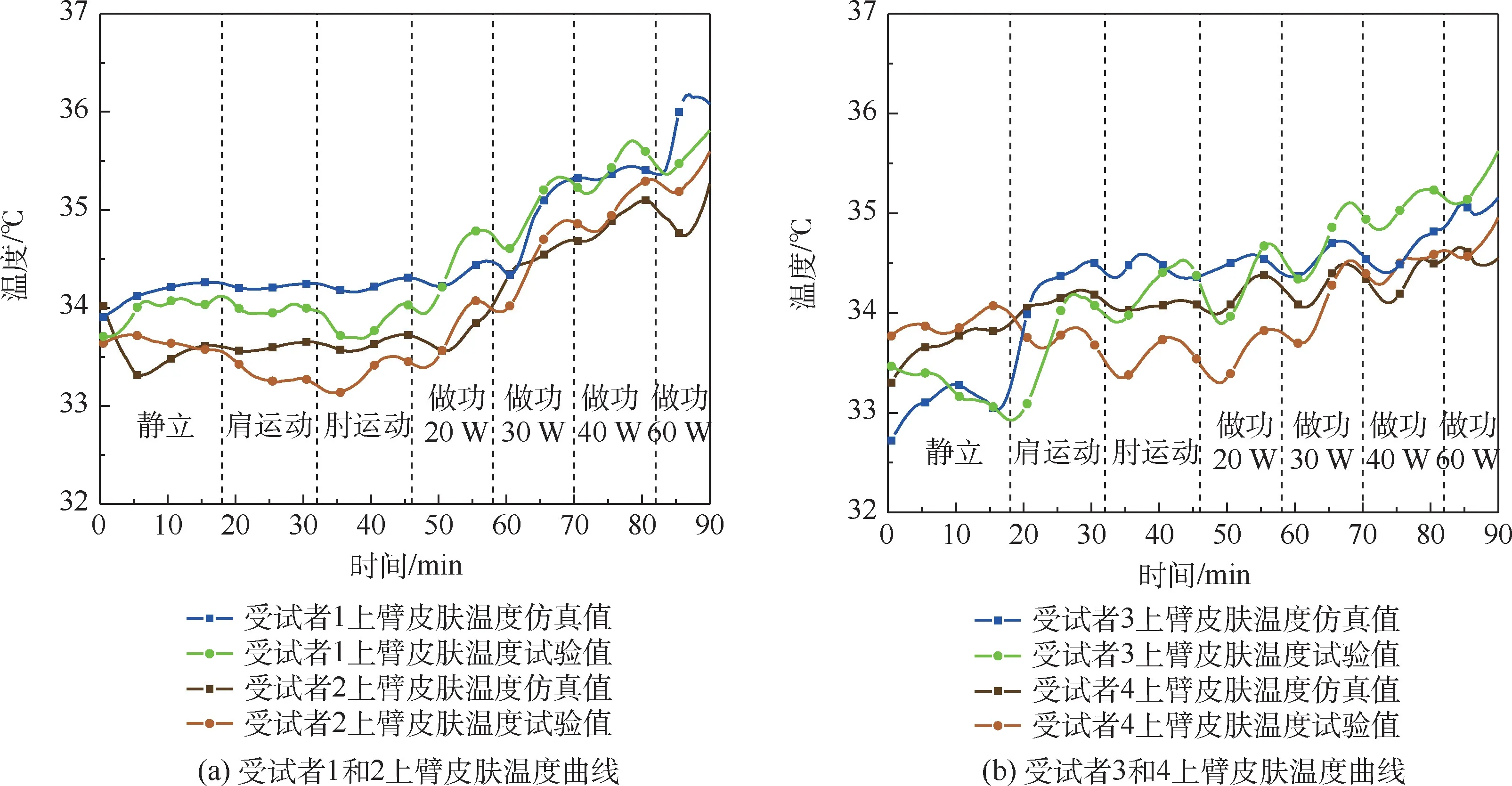
图9 上臂皮肤温度曲线Fig.9 Skin temperature curves of uper arms
图10 为手部皮肤温度曲线。 手部肌肉做功小,运动速度快,对流传热强,皮肤温度上升趋势弱。 手部皮肤温度曲线有明显的周期性波动—即在每个做功周期内,皮肤温度先下降后升高(运动时下降,休息时升高),这是做功和停歇的周期性活动引起代谢和对流散热变化而导致皮温的周期性改变:运动时手部与空气间有较大的相对运动,空气的对流传热大,皮温下降;休息时对流散热小,同时因人体传热的滞后性使得做功的代谢产热休息期间释放到皮肤表面引起皮温增加。 4 名受试者手部皮肤温度仿真值与试验值最大误差均小于0.8 ℃。
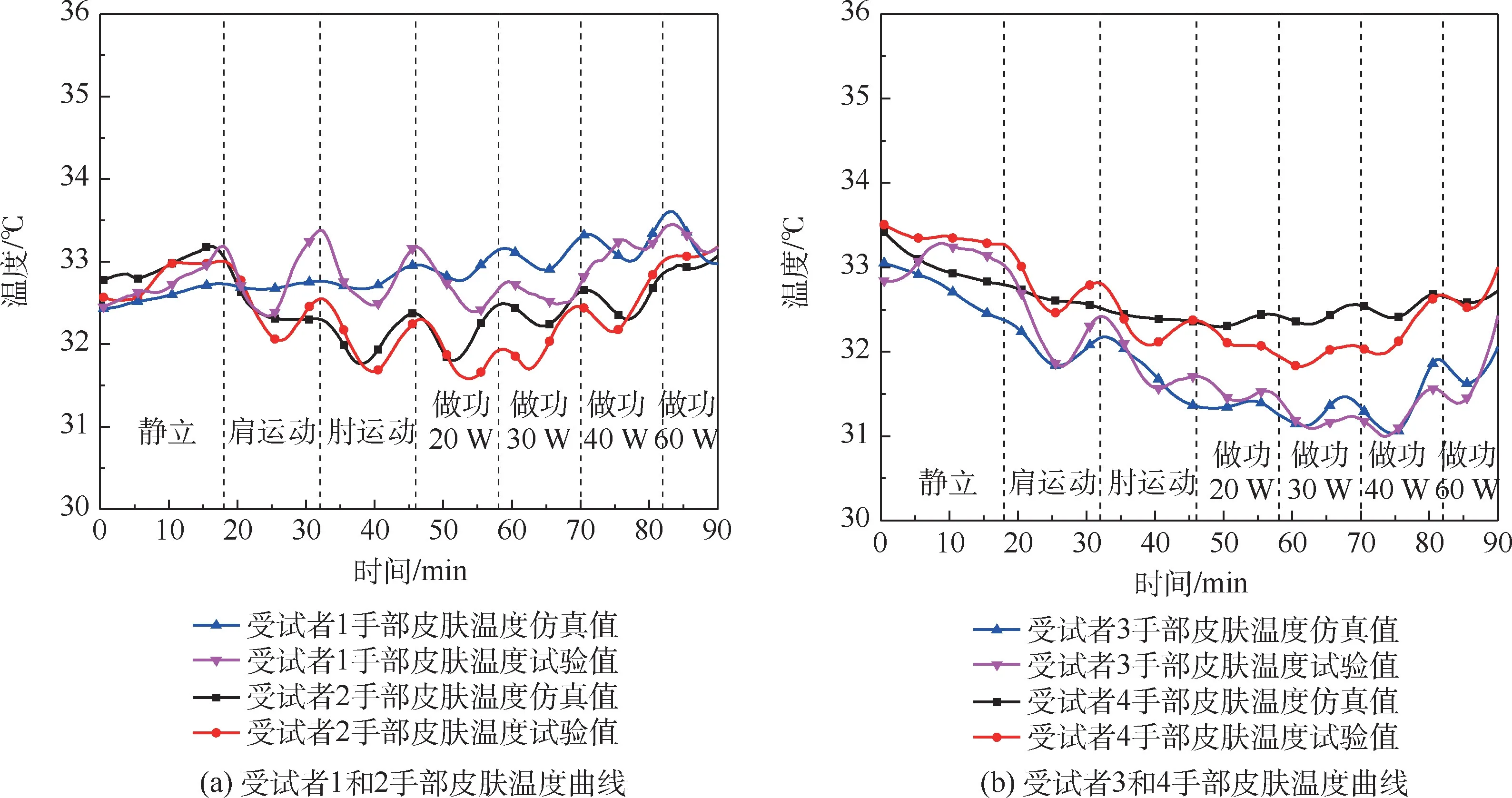
图10 手部皮肤温度曲线Fig.10 Skin temperature curves of hands
图11 为腿部皮肤温度曲线。 腿部皮肤温度曲线随做功增加,呈现略微上升趋势。 这是因为腿部离人体躯干近,做功产热通过血液循环系统容易将热量传输给腿部。 图11 中温度曲线在每个做功周期内表现出先下降后上升的波动性,也反应了人体代谢产热在人体中传递滞后的特点。4 名受试者腿部温度仿真值与试验值最大误差均小于0.5 ℃。
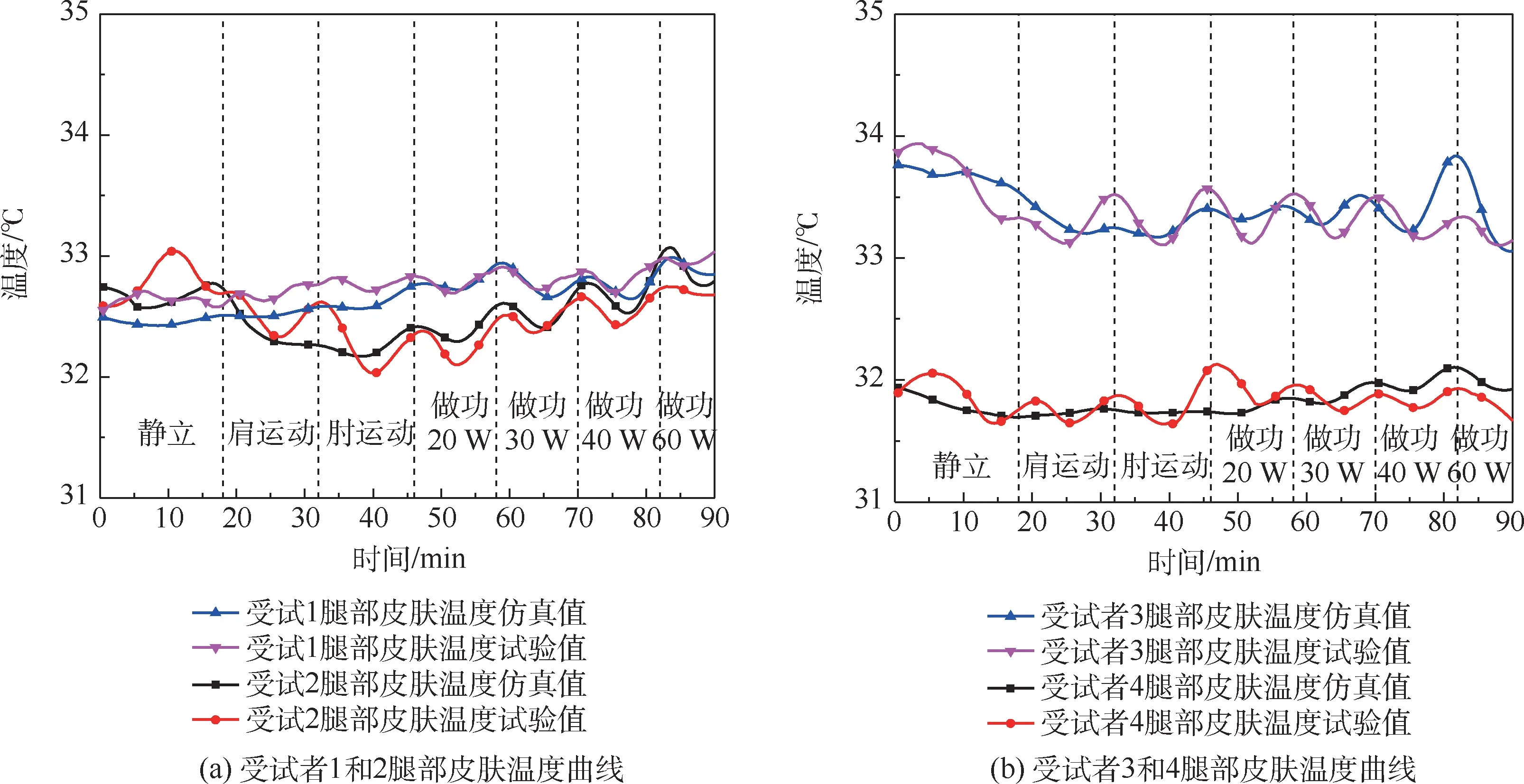
图11 腿部皮肤温度曲线Fig.11 Skin temperature curves of thighs
图12 为脚部皮肤温度曲线。 脚部代谢产热小,离身体核心部位远,其皮温受外环境影响大,因此4 名受试者脚部皮肤温度变化趋势有不同。图12 中30 W 以上对外做功周期内脚部皮肤温度有较为明显波动,说明上肢中高强度周期性做功(30 W 以上)产热通过血液系统对脚部皮温会产生一定影响。 4 名受试者脚部温度仿真值与试验值最大误差小于0.5 ℃。
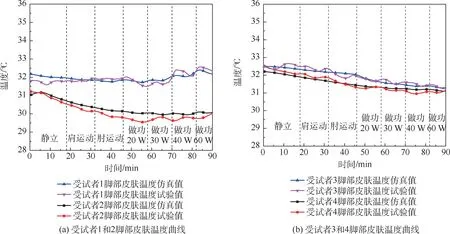
图12 脚部皮肤温度曲线Fig.12 Skin temperature curves of feet
图7 背部和图8 胸部皮肤温度曲线在起始段仿真与试验相比有较大偏差,随着时间变化偏差量逐渐减小,是由于各层组织初始仿真温度的设定与试验值存在偏差,随着计算迭代次数的增加,各层温度的仿真值与试验值逐步趋近。
4 结 论
1) 人体上肢运动代谢产热主要在上肢、背部和胸部相关肌肉群产生。 肌肉层中的代谢产热在人体中的传递表现出滞后性。
2) 上肢运动代谢产热对人体上部躯体产生的影响作用大于下部躯体。 头部、背部和胸部皮肤温度在中低负荷运动下变化不明显,与这些部位汗腺分布密集散热能力强有关。
3) 上肢运动代谢产热通过血液系统传递到远端肢体手和足的份额小,对手和足皮肤温度影响弱。
4) 模型对各部位皮肤温度的仿真值与试验值吻合度较高,最大偏差量小于0.8 ℃。 误差主要来源有以下5 个方面:①人体核心层、肌肉层和脂肪层温度的初始值无法测量,其值引用了相关文献数据,与真实值存在偏差;②人体模型中皮肤层节点温度代表一个部位整个皮肤层温度,而试验中的皮肤测点温度只是局部皮肤点温度,二者实质物理含义不同,只是作为近似处理;③温度传感器与皮肤间有接触热阻,而且运动时会产生相对滑动,并伴有气流影响,所以测试值与真实值存在偏差;④人体热模型发展不完备,模型中内置的各类物性参数和控制参数对真实物理过程的反映有一定误差;⑤模型对衣物在人体向外环境散热中的作用进行了简化处理,即用恒定的衣物热阻和湿阻的测量值来描述衣物在散热环节的阻力作用。 这样的简化虽然对吸湿性小的纤维制做的服装是合理的,但简化处理将不可避免的引入误差。
综上所述,本文中将Tanabe 模型与Smith 模型中基于试验获取的人体热调节控制经验方程相结合,再通过合理简化衣物热模型,设置各类物性参数、控制参数和边界初始条件,进而抓住了人-服-环境系统热质传递的主要特征和机理。 模型对试验设置的常温环境下中高强度运动中人体皮肤温度的热响应具有一定的预测能力。
