基于PCA-HicksHenne 方法的几何不确定性稳健优化设计
2023-01-12张威王强路嘉晨阎超
张威, 王强, 路嘉晨, 阎超,*
(1. 北京航空航天大学 航空科学与工程学院, 北京 100191; 2. 中国航天空气动力技术研究院, 北京 100074)
在飞行器的整个寿命周期中存在着各种各样的不确定性,而考虑不确定因素的气动优化研究在飞行器气动外形设计中扮演着至关重要的角色。 考虑不确定性因素的优化设计主要包括稳健优化设计[1]及可靠性优化设计[2]。 稳健设计的优化目标是为了在性能提升的同时降低目标函数对不确定因素的敏感度,而可靠性设计则是为了降低故障概率。 本文的关注点主要在于稳健优化设计研究。 现有的稳健优化设计主要着重于针对环境扰动下的优化设计研究,而对于几何扰动的关注则相对较少。
对于几何不确定性的考量,主要有2 方面:①局部位置的凸起凹陷,主要是由于工作状态下的磨损、侵蚀等导致的。 由于其大小、位置、形状、分布形式等较为依赖对大量实验数据的分析,而实验数据难以获取使得该类几何不确定性量化也较难实现。 ②加工过程中存在不确定性。 现有对该类几何不确定性的研究中,由于认知不足,或是根据经验直接在如翼型前缘等关键位置添加满足正态分布的几何扰动[3],然后进行不确定性量化;或是采用区间法[4]直接进行几何不确定性量化。 这些方法的使用,无论是对正态扰动添加位置的选择与确定,还是区间法的直接应用,经验性都较强,忽视了对于全局的考量,及潜在几何模态的影响。
本文以RAE2822 翼型为例,采用主成分分析(principal component analysis, PCA)方法[5-6],对整个参数化过程进行分析,增强对全局范围内主要几何变形模态的认知,了解对应参数的分布规律。 应用敏感度分析方法,针对不同目标函数(以升力系数、阻力系数、翼型厚度等为例),找出主要变形控制模态,作为几何扰动来源。 同时,进行了考虑几何不确定性的稳健优化设计研究。
1 PCA-HicksHenne 方法
1.1 Hicks-Henne 参数化方法
Hicks-Henne 方法[7]是常用的参数化方法,本文以此对RAE2822 翼型进行参数化,具体的几何外形表达式如下:
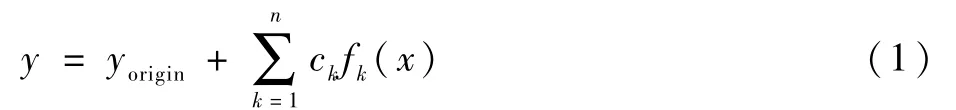
式中:y为变形后翼型的上(下)表面函数;yorigin为初始翼型的上(下)表面函数;fk(x)为扰动型函数,ck为对应参数。
原始的Hicks-Henne 方法中的扰动型函数定义如下:
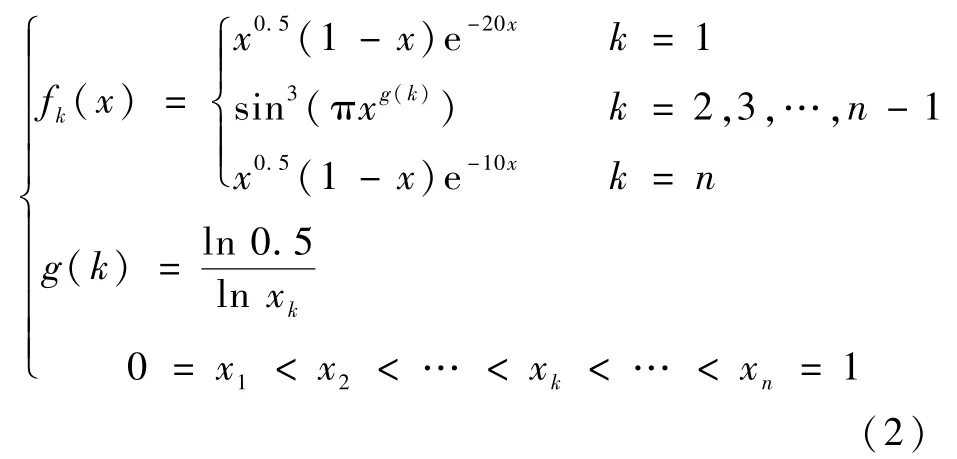
研究表明[8-9],该方法存在后缘扰动不足的问题。 对此,本文将翼型后缘扰动函数做了式(3)的修改。 其导函数(式(4))在后缘处取值不为0,可以提供有效的后缘扰动。

1.2 PCA 方法
PCA 是一种常用的数据降维方法。 通过对高维特征数据进行降维,仅保留重要特征,从而实现数据处理效率的提升。
基于最近重构性或最大可分性[10],可将PCA的优化目标写为
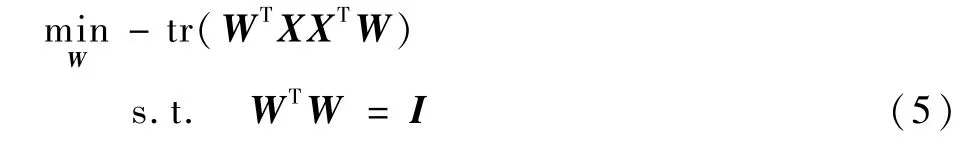
式中:X为翼型样本几何向量组成的矩阵;W为协方差矩阵XXT的特征向量矩阵;I为单位矩阵。
采用拉格朗日乘子法可得

式中:wi为矩阵W第i列的向量,也是XXT的特征向量;λi为对应的特征值。
因此,仅需对协方差矩阵XXT进行特征值分解,得到特征值如式(7)所示。 一般对所得到的特征值按照由大到小顺序进行排序,特征值越大,表明对应的“成分”的贡献越大。 随后再选取前d′个特征值对应的特征向量W*= (w1,w2,…,wd′),即为主成分分析的解。 特征值由大到小如下:

1.3 PCA-HicksHenne 参数化方法
采用PCA 方法,对经由Hicks-Henne 方法得到的大量翼型进行分析,提取目标翼型变形的主要模态,并以此为基础对翼型进行变形。 该方法可以提高对翼型变形内在几何模态的认知,进一步降低参数化所需参数维度,提高效率,这就是本文所采用的PCA-HicksHenne 方法。
以RAE2822 翼型为例,设定Hicks-Henne 方法中的型函数个数为21(上下翼面合计变量维度为42)。 较多的型函数个数可以赋予参数化方法更好的设计空间表达能力。 在给定设计空间内随机选取100 000 个样本翼型数据,如图1 所示,并对其进行PCA 分析。 给出前20 个主要变形模态所对应的能量分布,如图2 和图3 所示。 可以看出,前8 个变形模态表达了98% 以上的变形信息,这表明仅采用前8 个模态就能够很好地表征原设计空间中的翼型变形。
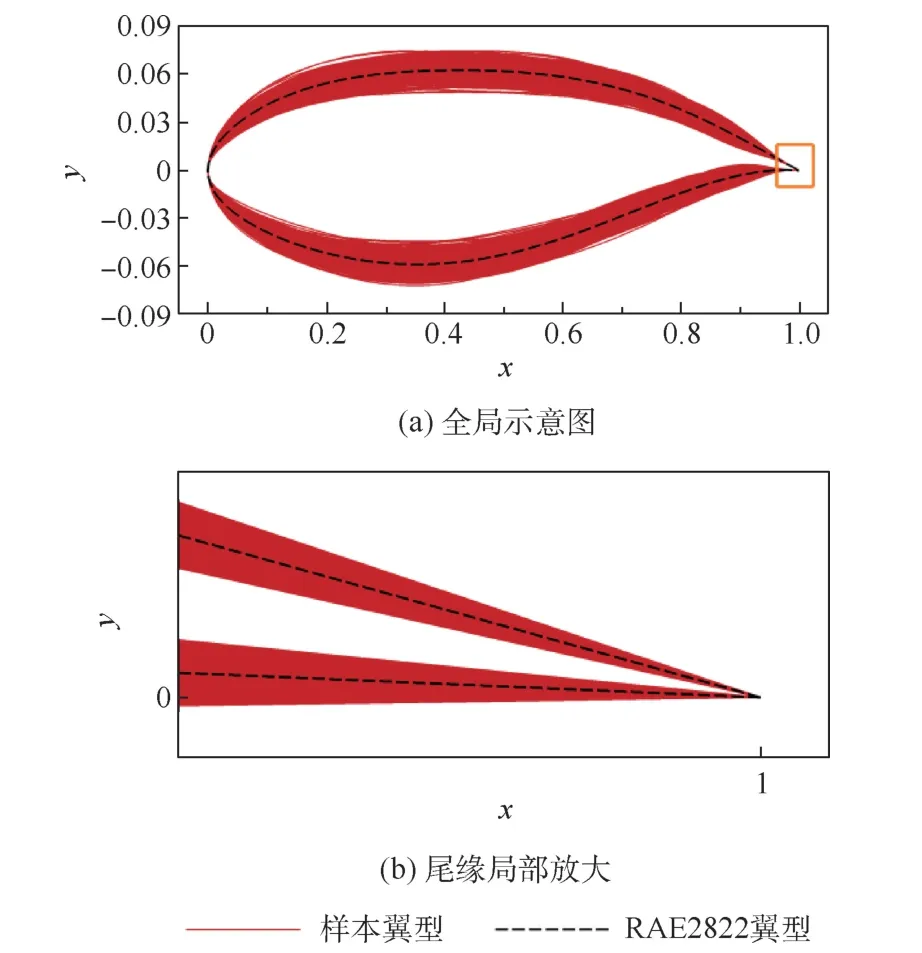
图1 样本翼型及RAE2822 翼型示意图Fig.1 Schematic of sample airfoils and RAE2822 airfoil
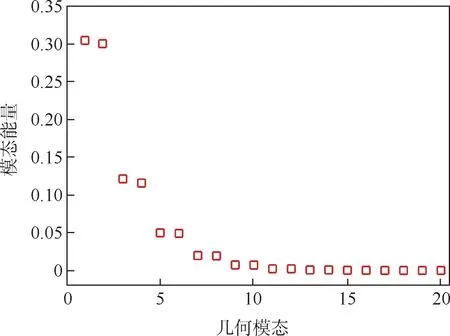
图2 主要几何变形模态对应模态能量分布Fig.2 Energy amplitude of main geometric transformation modes
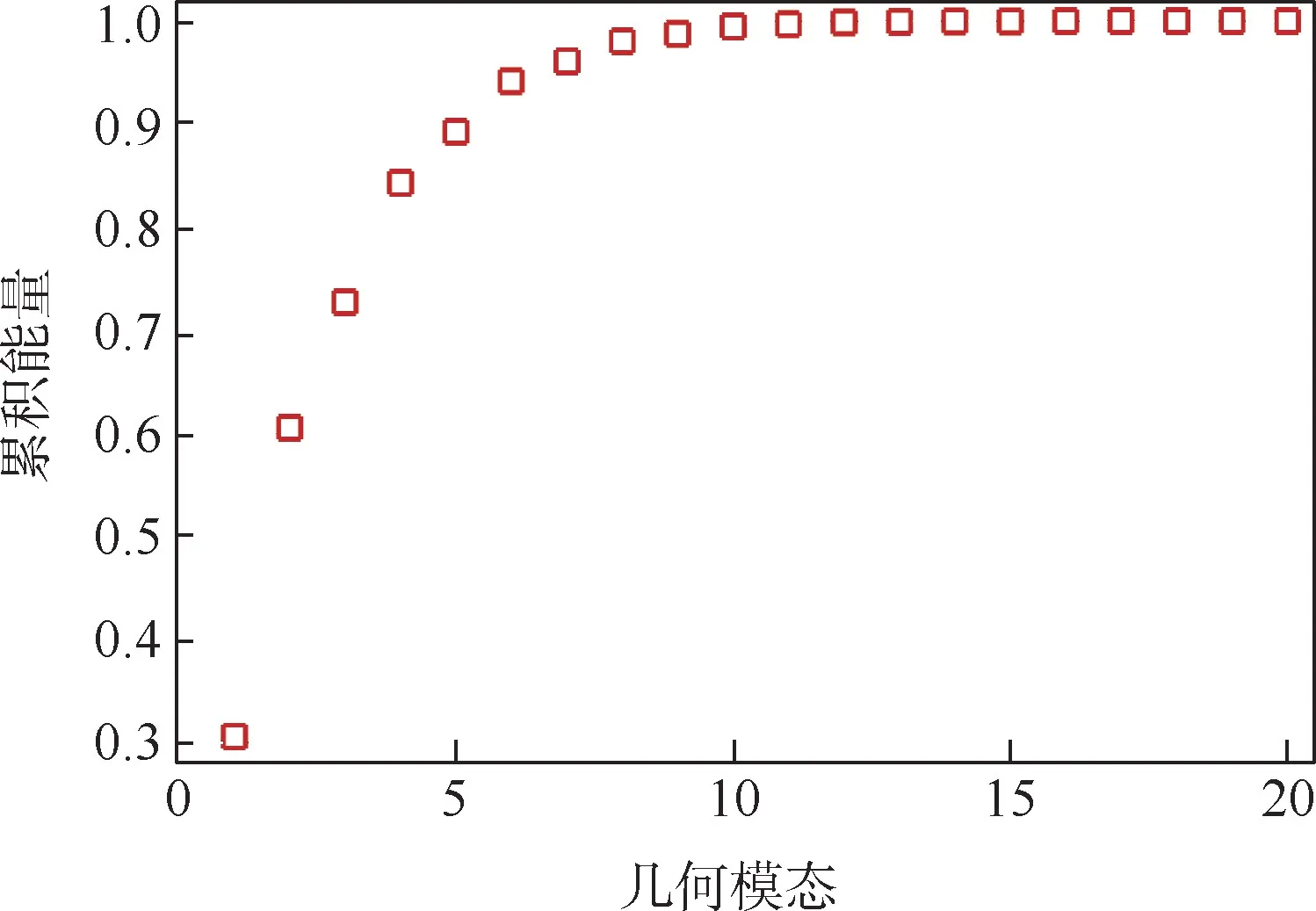
图3 主要几何变形模态对应累积能量分布Fig.3 Accumulated energy of main geometric transformation modes
图4 给出经PCA 分析得到的前8 个变形模态。 模态1 和模态2 分别为翼型的厚度变形模态及弯度变形模态,模态3 和模态4 分别为上下翼面的最大厚度位置的轴向位移模态,模态5 ~模态8 则分别为翼面的挤压模态。
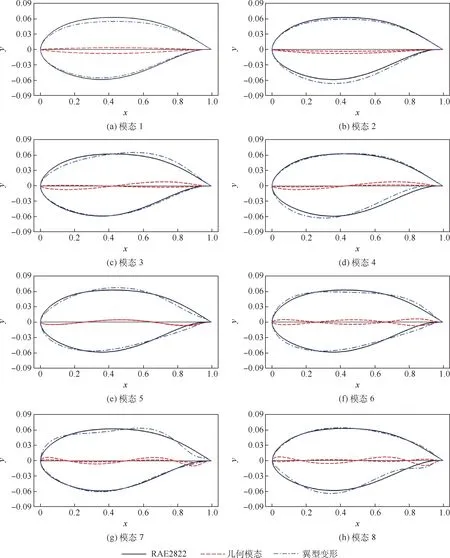
图4 主要几何变形模态示意图Fig.4 Schematic of main geometric transformation modes
本文以这些模态为设计变形模态,通过线性叠加到基准翼型RAE2822 上,从而实现翼型的变形。 同时,观察本节随机选取的100 000 个翼型对应在这8 个模态构建的参数空间中的参数分布情况,如图5 所示。 观察可知,所有模态的参数分布与N(0,0. 012)的正态分布几乎完全一致,因此,可以认为第3 节中所用到的不确定模态也满足正态分布。 同时将各模态参数的设计范围定义为[ -0.03,0.03],以满足99.7% 以上的参数变化范围。
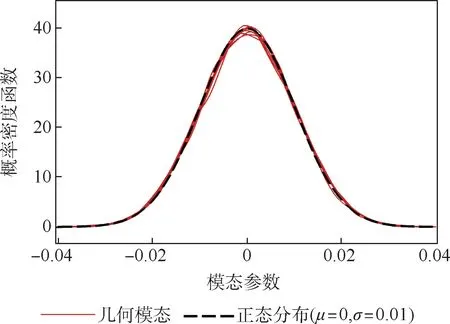
图5 主要几何变形模态对应参数分布情况Fig.5 Parameters distribution of main geometric transformation modes
2 重要参数识别
本文的主要目的是为了发展基于PCA-Hicks-Henne 参数化方法的几何不确定性稳健优化设计方法。 因此,为了选定特定参数模态作为几何扰动模态,需要对各模态针对目标函数(如升力系数、阻力系数、翼型厚度等)的参数敏感度进行分析。
Sobol 指数方法是一种常用的全局参数敏感度分析方法[11-12]。 通过Sobol 指数方法,可以得到各参数对于目标函数的影响,主要包括参数的主指标、参数之间的交互指标及参数的总指标。参数的主指标是指完全由该参数产生的影响;交互指标是指参数之间相互作用,共同产生的影响,通常用来判断参数之间是否存在关联;总指标则是由参数主指标与交互指标共同组成,通常表示该参数产生的所有影响的总和。
本文以RAE2822 翼型的升力系数、阻力系数、翼型厚度为目标,研究第1 节中所得的各变形模态在设计空间内的参数敏感度,结果分别如图6 ~图8 所示,计算状态如表1 所示。 可以看出,对于升力而言,模态2 是主要影响模态,这是由于跨声速条件下翼型弯度是升力产生的主要来源;对于阻力而言,模态3 是主要影响模态,这是由于在模态3 下,上翼面的最大厚度位置在轴向上发生变化,导致上翼面激波产生位移,激波强度、激波阻力发生变化,从而阻力发生变化;对于翼型厚度而言,模态1 即厚度变形模态是主要影响模态。
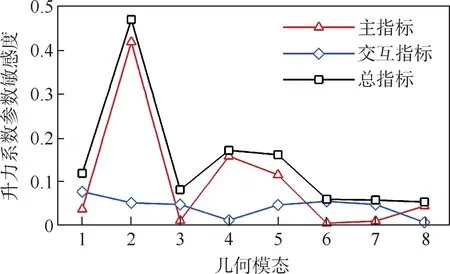
图6 升力系数的参数敏感度分析Fig.6 Parametric sensitivity analysis of lift coefficient
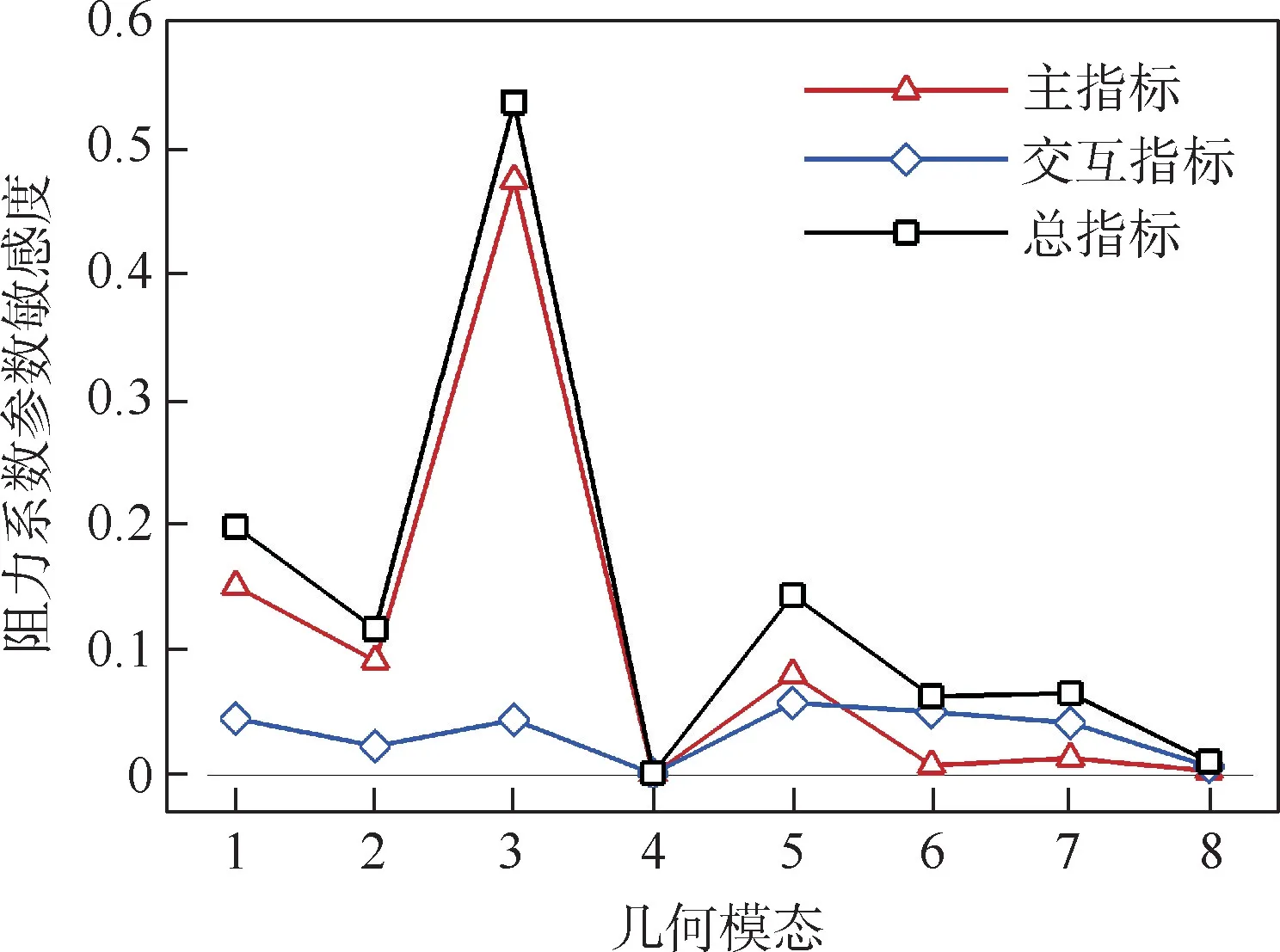
图7 阻力系数的参数敏感度分析Fig.7 Parametric sensitivity analysis of drag coefficient
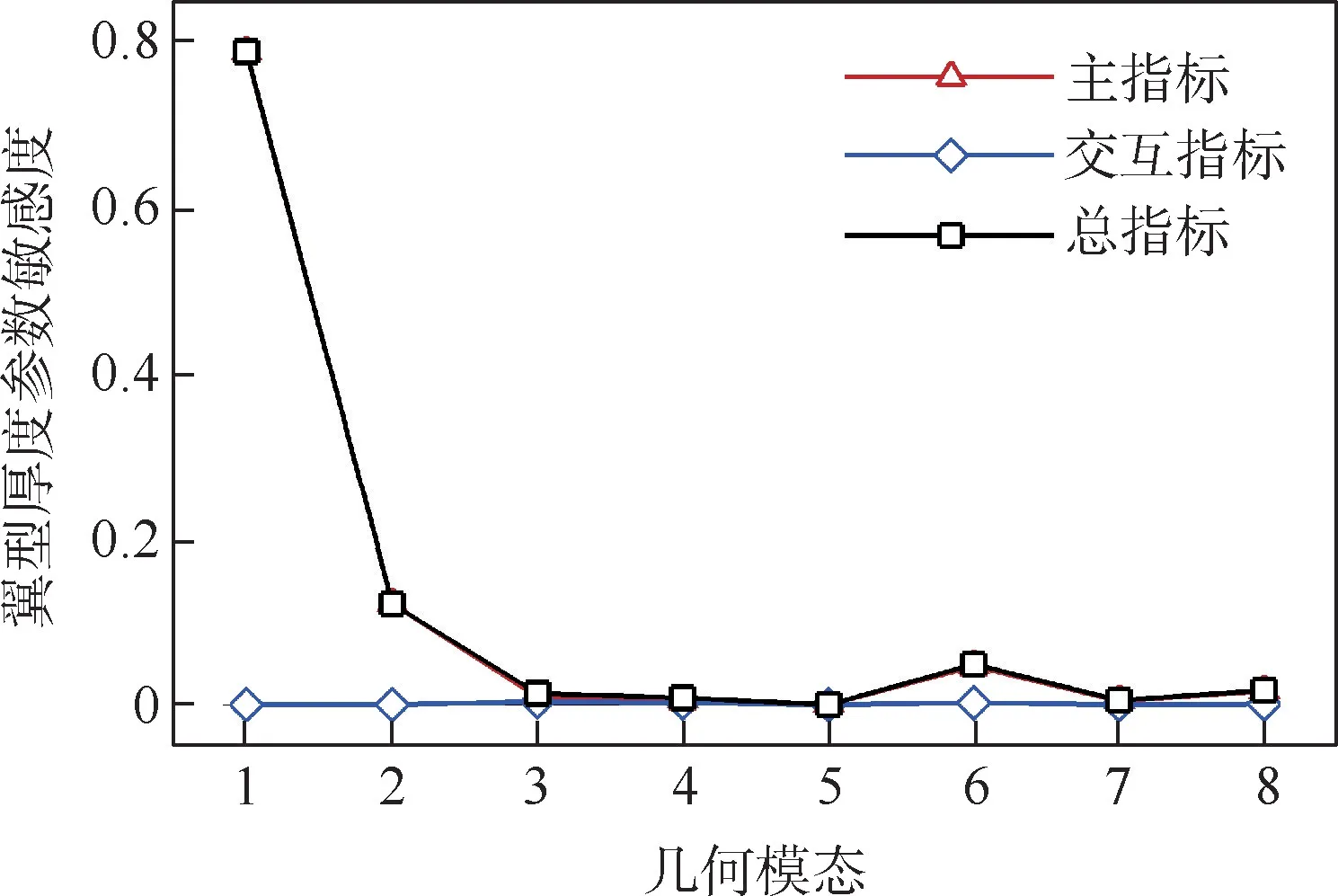
图8 翼型厚度的参数敏感度分析Fig.8 Parametric sensitivity analysis of airfoil thickness

表1 计算状态Table 1 Computational condition
因此,模态1 ~模态3 是翼型性能的主要影响模态。 这些模态的微小变化,会对翼型性能产生较大的影响。 因此,本文选取这3 个模态作为主要几何扰动模态,进行稳健优化设计。
3 几何扰动定义
在进行稳健优化设计之前,还需对几何扰动模态的参数进行定义。 根据第1 节研究结果,可以假定3 个扰动模态仍满足正态分布,其均值为0。 为更好展现本文方法的性能,分别设定扰动模态参数的标准差为设计参数的0.2 ~0.4 倍,在基准RAE2822 翼型上,探索这些不同标准差假设下几何扰动的影响。
混沌多项式方法是一种广泛使用的不确定度量化分析方法[13-14]。 本文选用二阶混沌多项式方法来量化不同扰动量下的翼型升力系数、阻力系数、翼型厚度的不确定度,结果如表2 ~表4 所示。 可以看出,随着几何扰动量的增大,各个目标函数的不确定性都在增强。 同时也注意到,0.4 倍扰动量下,99.7% 置信区间的翼型厚度变化范围达到10 倍风洞模型允许公差[15],远远偏离实际允许情况,不予考虑。
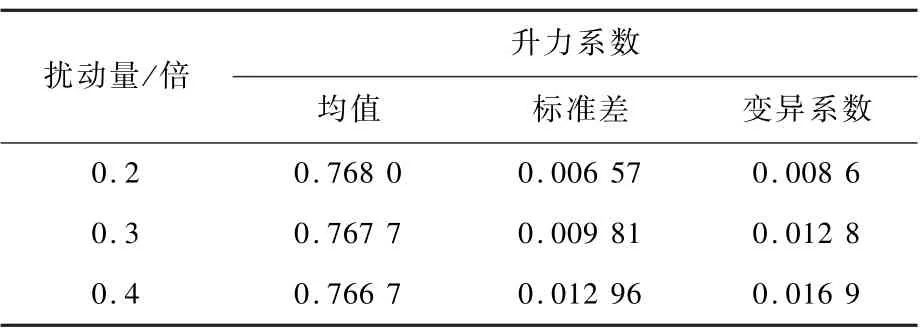
表2 不同扰动量下升力系数的不确定度对比Table 2 Comparisons of lift coefficient uncertainty under different perturbations
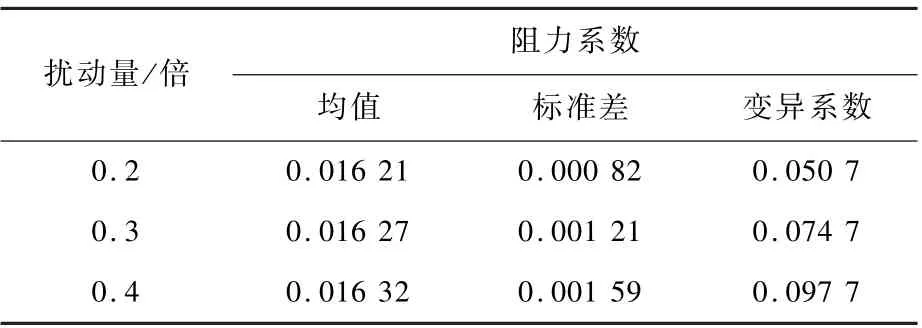
表3 不同扰动量下阻力系数的不确定度对比Table 3 Comparisons of drag coefficient uncertainty under different perturbations
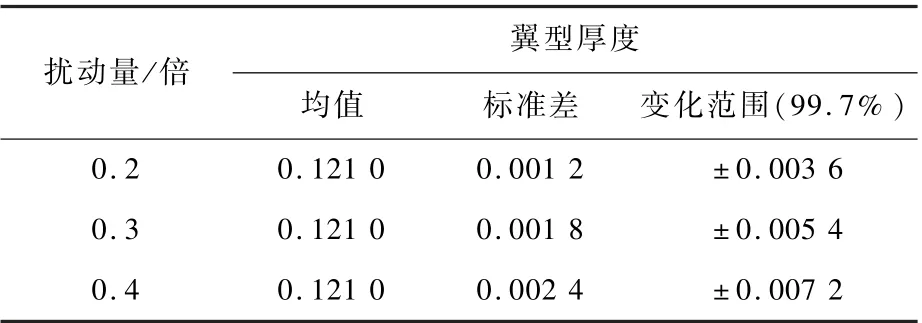
表4 不同扰动量下翼型厚度的不确定度对比Table 4 Comparisons of airfoil thickness uncertainty under different perturbations
因此,在第4 节的稳健优化设计中,定义模态1 ~模态3 为几何扰动模态,符合正态分布,均值为0,标准差为0. 3 倍的设计参数标准差(即0.003)。 扰动下的翼型变化情况如图9 所示。
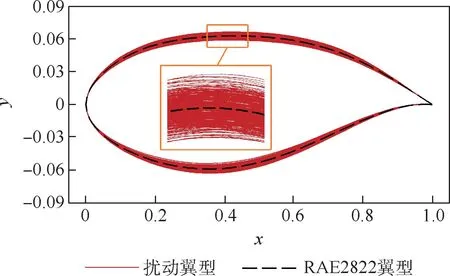
图9 几何扰动下的翼型变化情况Fig.9 Airfoil transformation under geometric perturbation
4 稳健优化设计
4.1 优化流程及计算说明
图10 给出了几何扰动下的稳健优化设计流程。 在无扰动的常规优化流程中,先对初始外形进行PCA-HicksHenne 参数化设计;其次对参数进行试验设计,得到采样点;再次进行配套网格变形及计算流体力学(computational fluid dynamic,CFD)解算,得到采样点的响应;随后在采样点上构建代理模型,并进行优化算法寻优;最终得到优化外形。 而在考虑几何扰动的优化流程中,还需要在参数化完成之后进行敏感度分析,寻找几何扰动参数,并根据CFD 结果进行扰动下的不确定度量化,随后再构建代理模型、进行算法寻优。
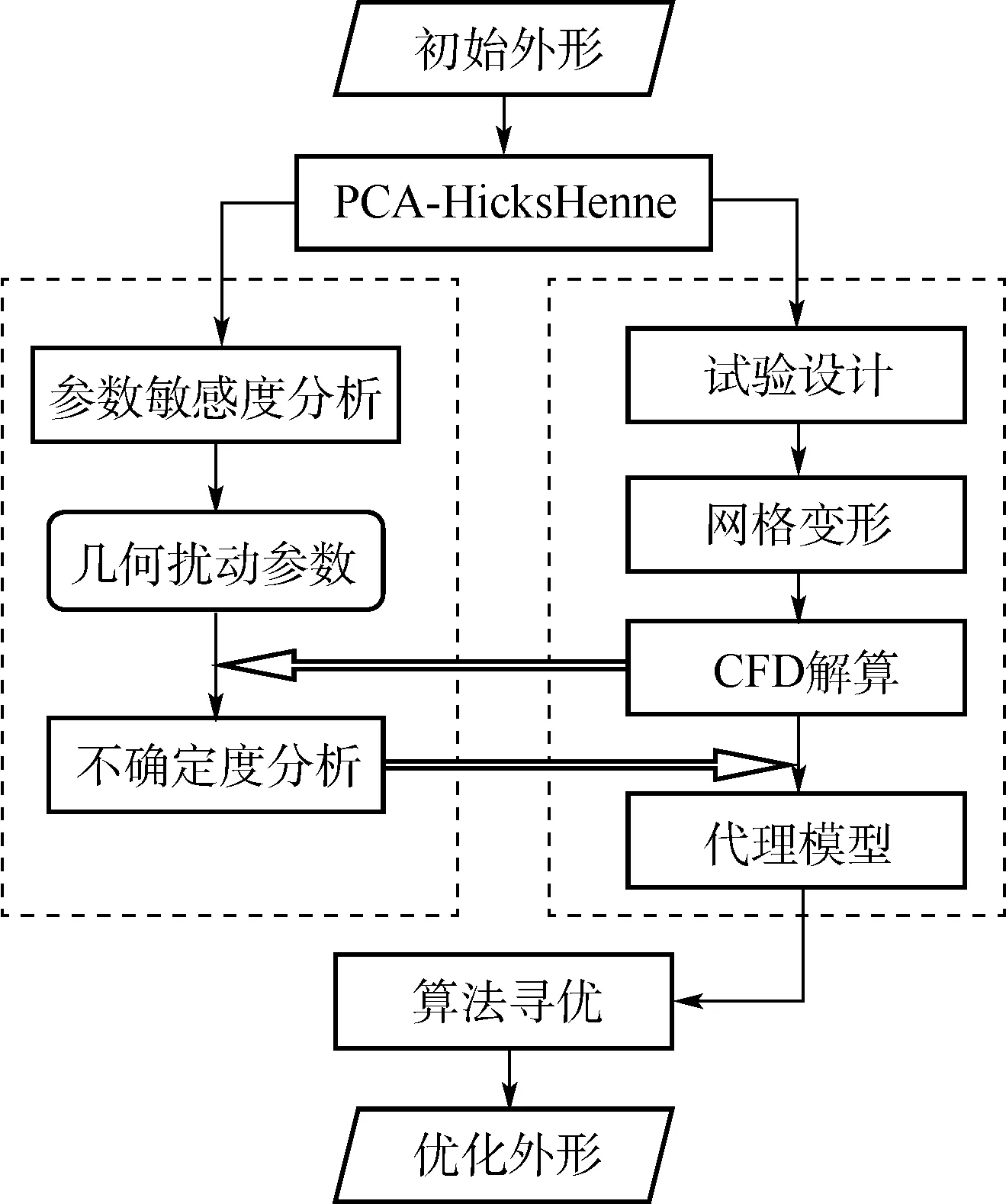
图10 几何扰动下稳健优化设计流程Fig.10 Flow chart of robust optimization design under geometric perturbation
本文选取RAE2822 翼型作为基础翼型,在自研CFD 计算平台MI-CFD[16]上,构建克里金模型[17],并利用多岛遗传算法[18]进行寻优。 计算状态如表1 所示。 为展示稳健优化的性能,将其与确定优化的结果进行对比,具体见4.2 节和4.3 节。
4.2 案例1
本节案例是单目标优化案例。 确定优化目标及对应的稳健优化目标定义分别为
maxCl

式中:Cl和θ分别为翼型的升力系数和翼型厚度;μ和σ分别为对应下标变量在扰动下的均值和标准差。
优化结果如表5 所示。 本文中无扰动翼型的升阻力性能与扰动下平均性能接近。 可以看出,确定优化外形在升力均值方面提升很多,但同时也不可避免地伴随着升力标准差的增长。 性能提升的同时,不确定度也在增大,这是不利的。 而对于稳健优化外形,因为在优化过程中已经考虑了对不确定性因素的约束,所以在其性能提升的同时,不确定度基本无变化。
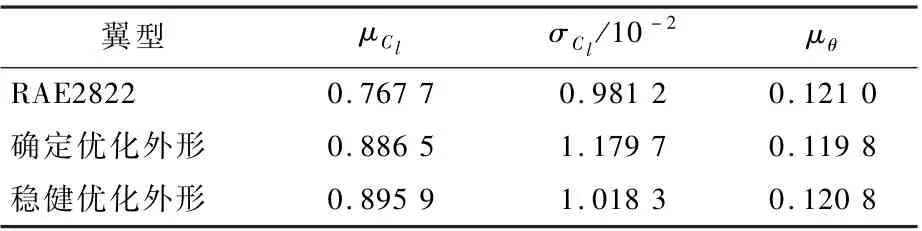
表5 案例1 优化结果对比Table 5 Comparisons of optimal results in Case 1
4.3 案例2
本节案例是多目标优化案例。 确定优化目标及稳健优化目标定义分别为

式中:Cd为翼型的阻力系数。
图11 和图12 给出2 个优化过程的Pareto前沿面,其中稳健优化结果仅给出平均升力与平均阻力的对应关系。 在图11 和图12 中分别选出3 个设计点,并将结果在表6 和表7 中列出。
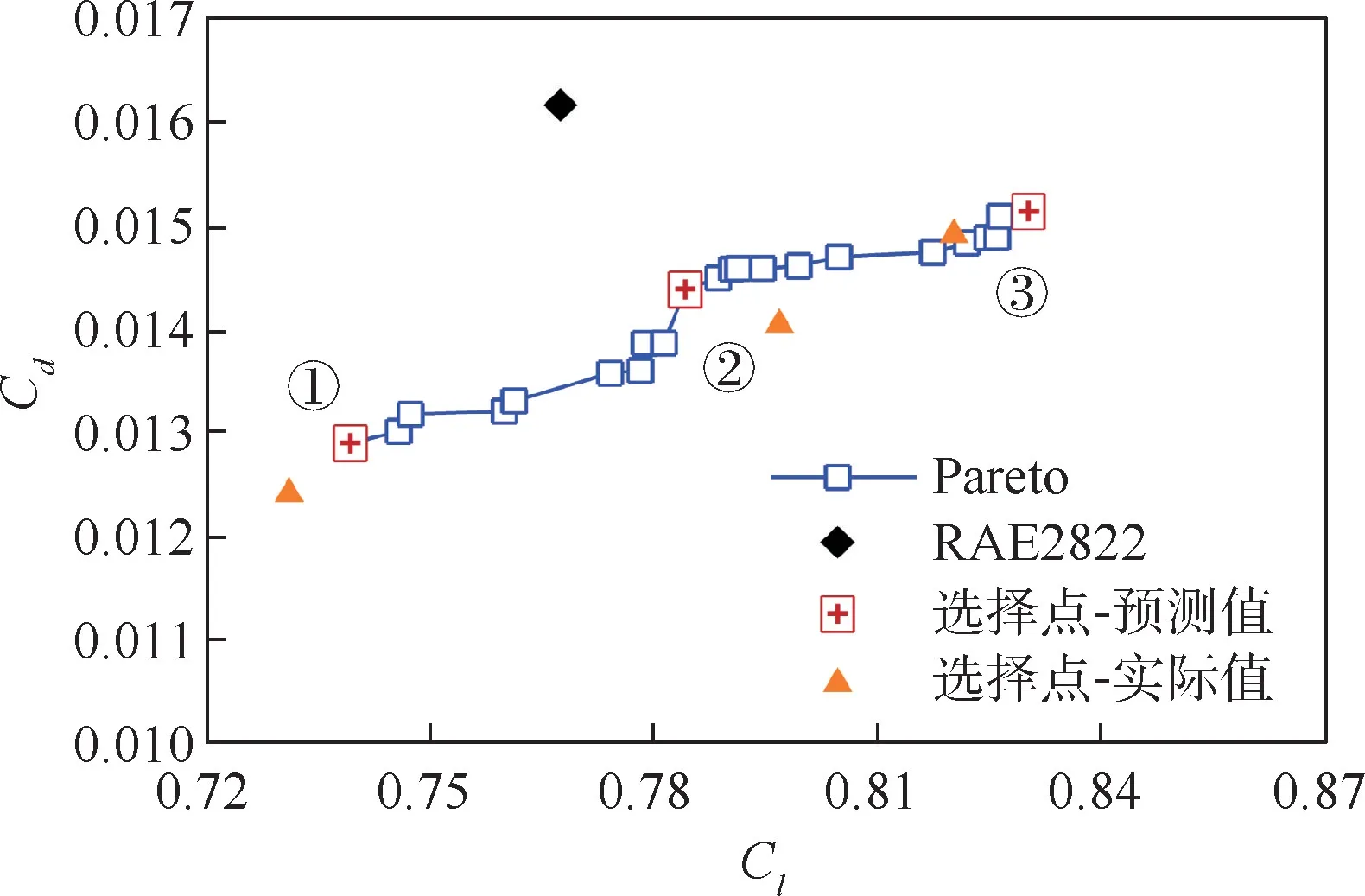
图11 案例2 确定优化Pareto 前沿面Fig.11 Pareto frontier of deterministic optimization in Case 2
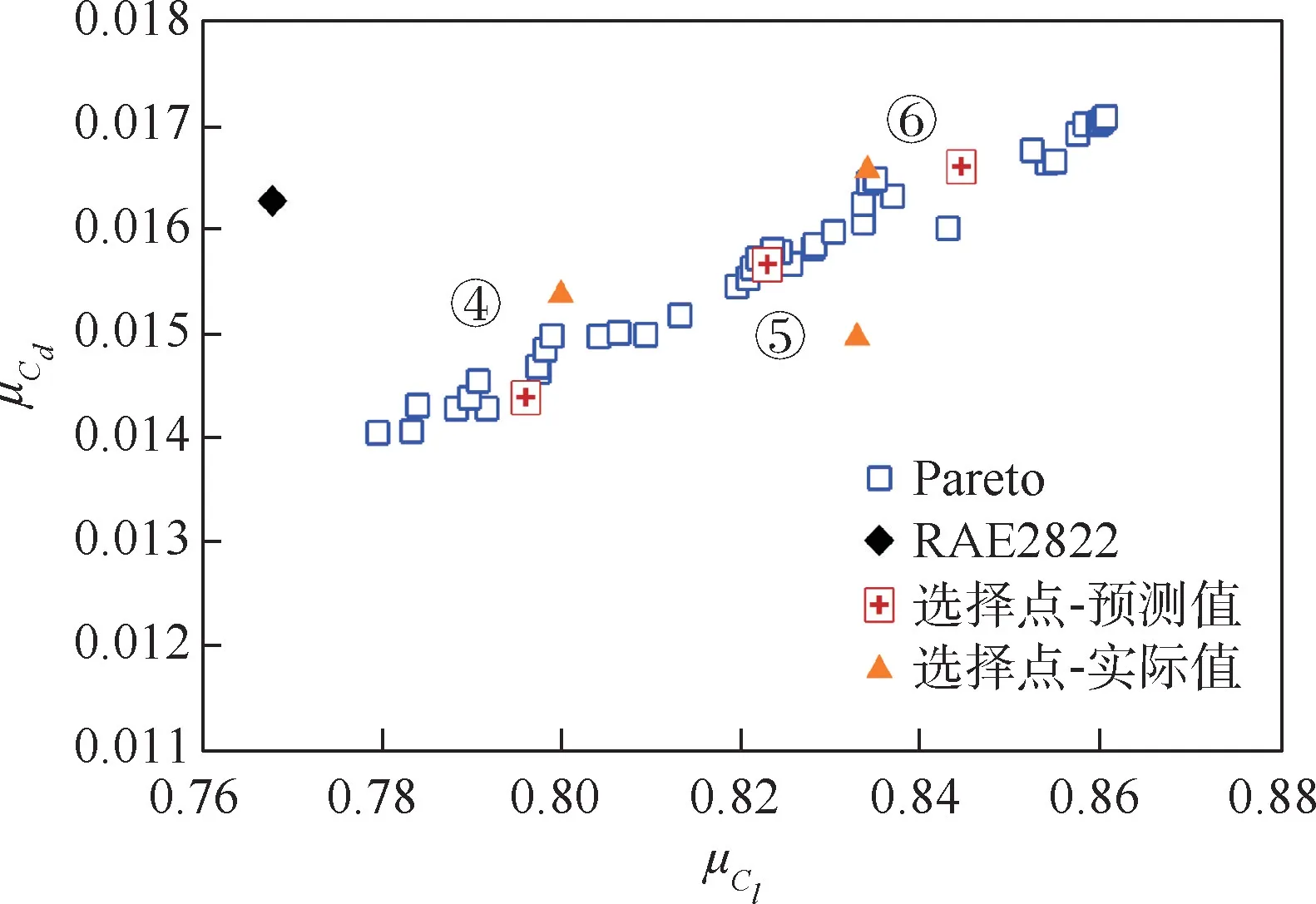
图12 案例2 稳健优化Pareto 前沿面Fig.12 Pareto frontier of robust optimization in Case 2
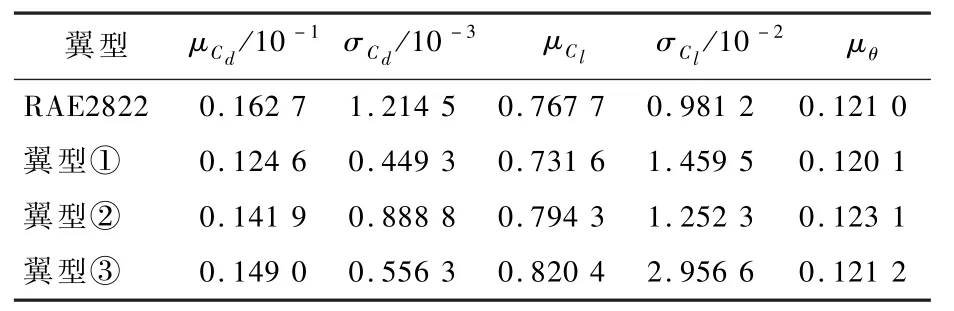
表6 案例2 确定优化结果Table 6 Solutions of deterministic optimization in Case 2
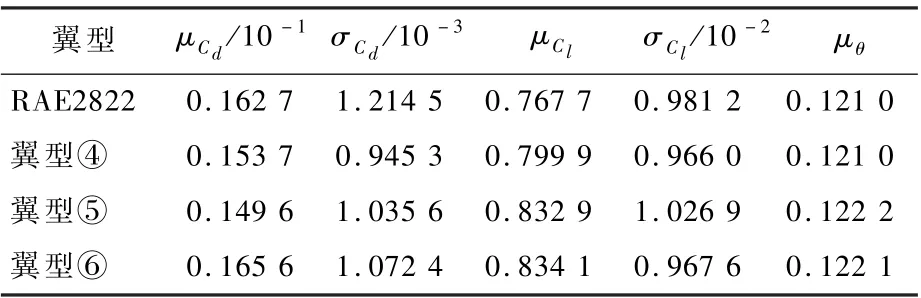
表7 案例2 稳健优化结果Table 7 Solutions of robust optimization in Case 2
如表6 和表7 所示,所有得到的优化翼型均满足翼型厚度约束。 其中,确定优化得到的3 个优化翼型在平均升阻力性能得到提升的同时,对阻力系数的不确定度恰好也有减弱的效果,而对升力系数的不确定度则恰恰相反。 3 个翼型的升力系数标准差均有不同幅度的增长,最高达到了近200%。 对于飞行器稳健性的设计要求,这是不利的。 而稳健优化得到的3 个优化翼型,则在目标性能相斥的情况下,兼顾了升阻力的均值及标准差等各方面的性能要求。 在提升某些方面性能的同时,也能保证其他性能的不恶化。
由表6 和表7 确定优化得到的翼型③(以下为确定优化翼型)和稳健优化得到的翼型⑤(以下称稳健优化翼型)的平均性能相近,对其作对比分析。
图13 给出了RAE2822 翼型、确定优化翼型及稳健优化翼型的形状对比,并在图14 ~图16中给出了3 个翼型及其对应扰动翼型的压力系数Cp的分布情况。
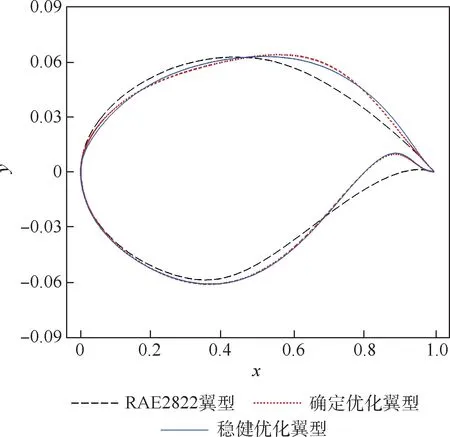
图13 优化翼型对比Fig.13 Comparisons of optimal airfoils
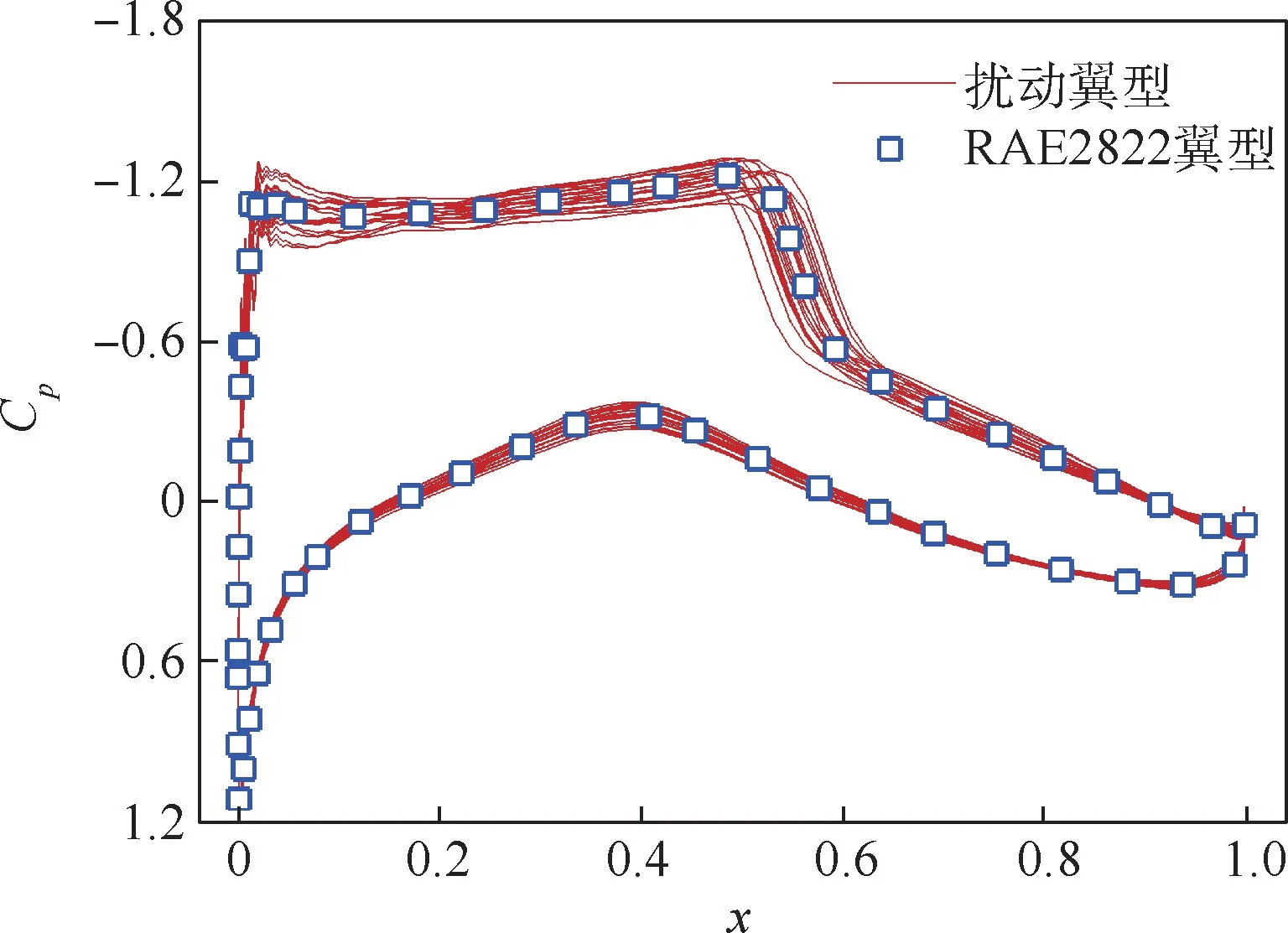
图14 RAE2822 翼型及扰动翼型的压力分布Fig.14 Surface pressure distribution of RAE2822 airfoil and its corresponding airfoils under perturbation
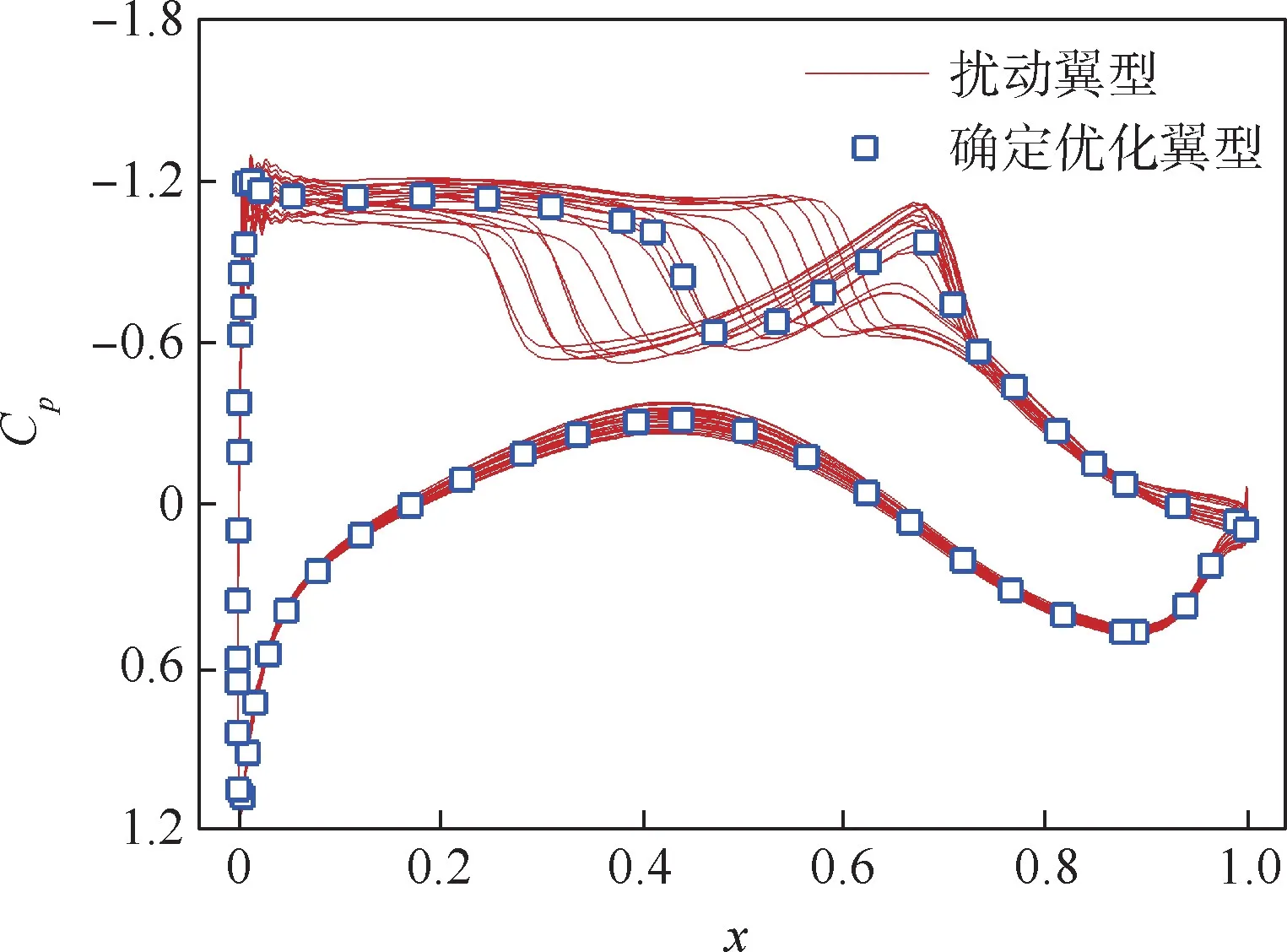
图15 确定优化翼型及扰动翼型的压力分布Fig.15 Surface pressure distribution of deterministic optimal airfoil and its corresponding airfoils under perturbation
如图13 ~图16 所示,在设计状态下,2 个优化外形在下翼面后缘附近都存在由于弯度增加的后缘加载,升力因此增加。 此外,稳健外形在上翼面前缘附近曲率更大,产生了一个较小的吸力峰,因此其升力相对更大。 而在阻力方面,2 个优化外形的上翼面相对RAE2822 翼型都更加平缓,确定优化外形分解为2 个小激波,稳健优化外形激波强度减弱,二者阻力均降低。

图16 稳健优化翼型及扰动翼型的压力分布Fig.16 Surface pressure distribution of robust optimal airfoil and its corresponding airfoils under perturbation
而在几何扰动下,稳健优化外形的激波强度和位置的变化与RAE2822 翼型相似,因此两者的升力系数变化几乎一致,标准差相当。 另外稳健外形的激波强度相对较小,因此其阻力系数的标准差也相对较小。 对于确定优化外形,其激波位置在扰动下变化剧烈,由此导致升力变化较大。而其激波强度较弱,变化也不大,因此阻力变化不大。
5 结 论
本文构建了基于主成分分析的PCA-HicksHenne参数化方法,并在此基础上进行了考虑几何不确定性的稳健优化研究,结论如下:
1) 对原始Hicks-Henne 方法进行了修改,使其在翼型后缘处也能提供有效扰动,提高了参数化方法的空间表达能力。
2) 构建了基于主成分分析的PCA-HicksHenne参数化方法,揭示了翼型的主要几何变形模态,验证了对应参数的分布规律,同时实现了参数化方法的降维,提高了优化效率。
3) 利用参数敏感度分析方法,发现翼型厚度变形模态、弯度变形模态及上翼面最大厚度位置的轴向位移模态是翼型性能的主要影响模态,必须予以重视。
4) 发展了基于PCA-HicksHenne 方法几何不确定性稳健优化设计方法,拓展了对几何不确定性稳健优化的研究,优化得到的目标翼型在性能提升的同时,稳健性也得以保证。
